固井界面接触热阻对井筒温度场预测的影响

段云星， 杨 浩

(中国地质大学(北京)工程技术学院， 北京 100083)

中国稠油资源丰富，已探明稠油地质储量20.6×108t，已动用地质储量13.59×108t，未动用地质储量7.01×108t[1]。目前稠油开采技术是通过热力开采，降低原油黏度，提高流动性，从而将其采出。在稠油热采过程中，高温工作液往复注停产生压缩、拉伸的交变载荷，导致套管产生变形、挤毁等损坏现象[2-3]。因此，井筒内温度场分布的预测精度影响到生产动态分析和生产方法优化，是安全、高效生产的前提。

Ramey[4]首先提出了井筒传热模型，将井筒传热分为两个部分：井筒内部纵向流体的流动传热，井筒径向与外部地层的传热。井筒纵向传热考虑蒸汽、多元热流体等的相变等因素；井筒径向的传热使用“总传热系数”法，考虑井筒内热量传到地层过程中油管、环空、套管、水泥环、地层的热阻作用[5]。

在建立稠油热采的井筒温度场预测模型时，大多数学者沿用了此方法。王谊[6]为分析特超稠油井注蒸汽生产中井筒及附近地层温度的影响因素，根据井筒各层介质的结构和物性的不均匀性，建立了井筒纵向上温度、压力和干度分布的模型，井筒径向的传热则使用“总传热系数”法。李伟超等[7]研究海上稠油开发中隔热油管导热系数、下入深度、多元热流体成分等工艺参数对热采效果的影响时，建立了热流体吞吐井的井筒温度场分布模型，沿井筒径向的传热使用“总传热系数”法。石岳[8]编制了注蒸汽稠油热釆井井筒温度场预测软件来研究生产中套管的损坏情况，井筒纵向传热为单相稳定流模型，井筒径向传热使用“总传热系数”法。刘婧斯[9]研究稠油蒸汽驱生产过程中的井底汽窜问题和防治措施时，建立的井筒温度预测模型使用了井筒径向“总传热系数”法。赵秋阳等[10]建立了超临界水进行稠油热采时的井筒传热模型，该模型使用“总传热系数”法处理井筒径向的传热。韩冰冰[11]建立适应于海上稠油热采井的多元热流体井筒流动与传热模型，并对注入含热水多元热流体和含蒸汽多元热流体的井筒散热情况进行分析时，井筒纵向的传热考虑了实际气体状态方程及其混合法则、井筒热容影响的瞬态导热函数，而井筒径向传热沿用“总传热系数”法。

这些研究中，沿井筒纵向的传热考虑了井筒内多相流(蒸汽、多元热流体等)的相变、压力等因素，不断接近实际生产情况；而井筒径向的传热，沿用了Ramey模型的“总传热系数”法，假设套管-水泥环-地层是紧密胶结的[4]。

在实际固井工程中，由于水泥浆体系适用性、井壁泥皮及掉块、钻屑清理不彻底，以及生产过程中套管内高温高压变化等问题，水泥环与套管和地层的界面存在微环隙[12-16]，在井筒径向传热过程中形成接触热阻[17]。

本文推导了固井界面微环隙充填气体时接触热阻的计算方法，设计了空气条件下测试地层-水泥环、水泥环-套管界面接触热阻的实验进行对比，最后分析了不考虑界面接触热阻的经典方法在计算井筒温度场时存在的偏差。

1 界面接触热阻

名义上光滑的固体表面从微观上看包含很多波峰和波谷。两个光滑固体界面接触时，仅在部分点发生接触，其他大部分空隙由气体等其他介质填充[17-20]。

热流经过接触面时，会聚集到接触点附近，出现接触热阻，如图1所示。

图1 接触面产生热流收缩示意图Fig.1 Schematic diagram of heat flow shrinkage caused by contact surface

固井界面微环隙充填空气时，接触面的热量传递有三种形式：接触部分两固体产生热传导、空隙部分有空气的热传导和固体间的热辐射。根据传热学理论[11,21]，各传热形式的热阻计算如下：

(1)在接触部分有固体间的传导传热，导热热阻为两固体热阻的串联：

(1)

式(1)中：R1为接触部分的导热热阻，(m2·K)/W；δ为接触表面的间距，m；λH、λC分别为高温固体和低温固体的导热系数，W/(m·K)。

(2)空隙部分有气体的传导传热。假设空隙充填介质的厚度相等，其导热热阻为

(2)

式(2)中：R2为气体的导热热阻，m2·K/W；λM为气体的导热系数，W/(m·K)。

(3)空隙部分会产生高温表面向低温表面的辐射传热过程。套管-水泥环-地层的接触界面可视为不可自见面的封闭系统，辐射换热量按式(3)计算：

(3)

式(3)中：ΦHC为高温表面向低温表面的辐射热量，W；EbH和EbC分别为高温表面和低温表面的辐射力，W/m2；εH和εC分别为高温表面和低温表面的发射率；AH和AC分别为高温表面和低温表面的面积，m2；XHC为AH对AC的角系数。

针对套管-水泥环-地层的接触界面，AH=AC=A，XHC=XCH=1。则式(3)简化为

(4)

(5)

式中：εS为系统发射率；A为界面名义接触面积，m2；σb为斯蒂芬-玻尔兹曼常数，σb=5.67×10-8W/(m2·K4)；TH、TC分别为高温表面和低温表面的温度，K。

辐射换热热阻计算式为

(6)

(4)将导热热阻[式(1)、式(2)]与辐射热阻[式(6)]进行并联，可得接触界面的接触热阻，如式(7)：

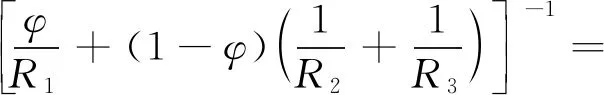
(7)

式(7)中：φ为真实接触面积与名义接触面积之比。根据赵兰萍等[22]的研究，即是两个固体的接触压力超过10 MPa，其真实接触面积也只是名义面积的1%～3%。所以本文中，取φ=3%。

2 测试仪器及试件

2.1 仪器介绍

本文所设计实验仪器如图2(a)所示。两试件轴向对齐并插入热电偶后，由绝缘材料包裹。试件组合的上端面由加压杆压住并利用杠杆原理来施加不同的接触压力；试件组合下端面由比例积分微分(PID)自动控制器控制的加热器来加热。K型热电偶通过小孔插入试件中，测量其中心线的温度分布；热电偶采集的温度数据通过带有NI TB-4353卡的NI PXIE-1078计算机采集；试件径向和热电偶由75 mm厚的纳米多孔绝缘材料包裹，这种材料在300～770 K的平均导热系数为0.025 W/(m·K)，因此可以忽略试件的径向散热，认为轴向是一维传热情况。

根据热电偶记录的两试件轴向温度分布，计算出两试件接触界面的接触热阻。试件尺寸和热电偶位置如图2(b)所示。实验步骤如下：

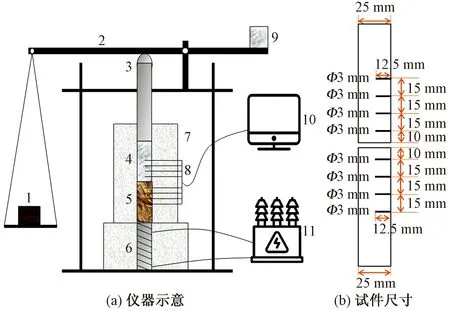
1为砝码托盘；2为杠杆；3为加压杆；4、5为试件；6为加热器；7为纳米绝热材料；8为热电偶；9为配重；10为集电脑；11为变压器图2 仪器和试件简图Fig.2 Schematic diagram of the equipment and specimen

(1)实验前，调节配重来平衡杠杆自身的重量，并保持杠杆处于水平位置，以保证后续添加砝码时杠杆对加压杆的压力是竖直向下的；加压杆把杠杆压力和自身重力传递给试件组合，便是两试件接触面的压力。对杠杆进行受力分析，如图3所示，计算不同砝码重量时试件的接触压力。

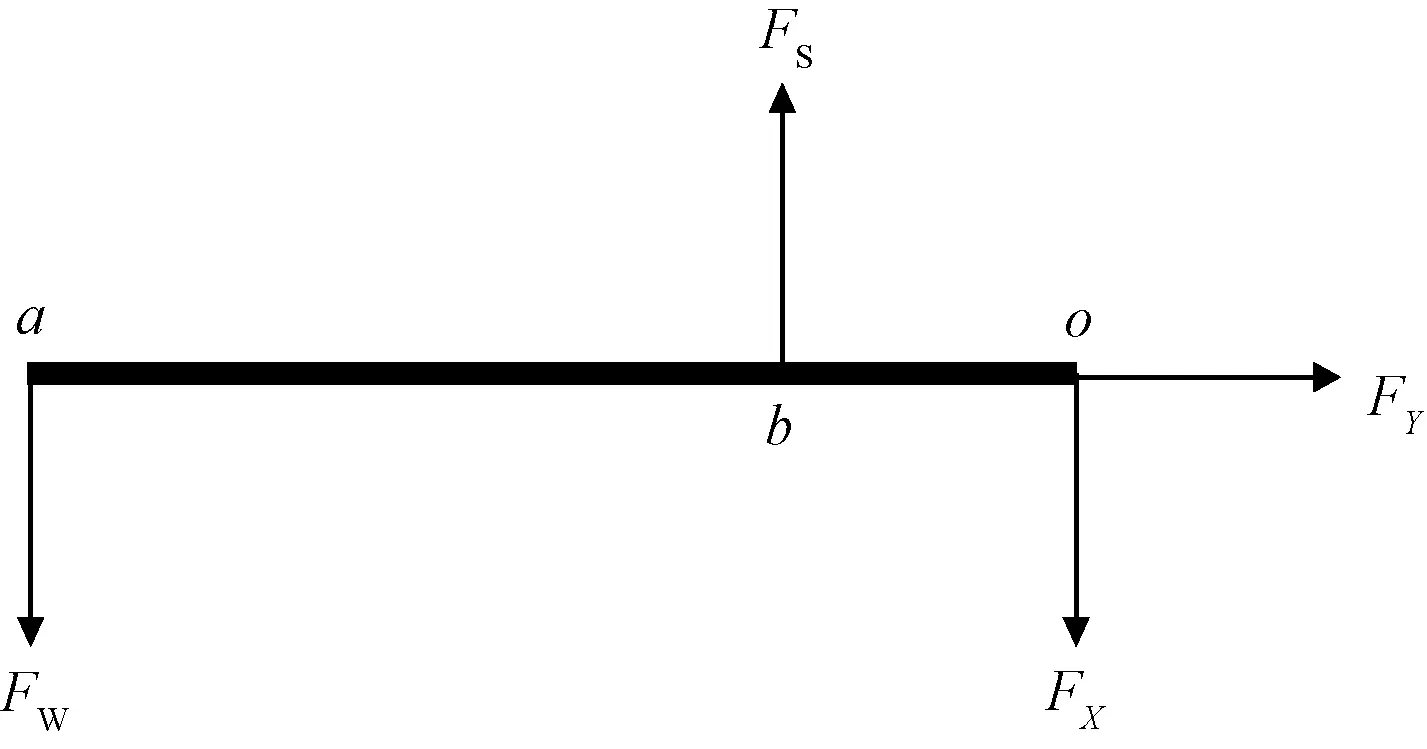
a为挂砝码处；FW为砝码重力；b为加压杆与杠杆接触处；FS为杠杆受到加压杆的支持力；o为铰接处，杠杆受力可分解为水平方向FY和竖直方向FX图3 杠杆受力示意图Fig.3 Stress diagram of lever

对o点力矩平衡：

FWLao=FSLbo

(8)

根据牛顿力学定律，加压杆受到的杠杆压力与FS大小相等。试件受到的接触压力为

(9)

式(9)中：Gg为加压杆重力，N；S为试件与加压杆的接触面积，m2。

(2)安装好试件和热电偶，包裹好绝缘材料，如图4所示。

(3)打开数据记录电脑，开启加热炉并设定在目标温度；当加热炉温度和所有热电偶的温度在30 min内变化小于0.2 K时，认为系统温度达到稳定，记录热电偶的温度数据。

(4)增加砝码重量，重复(3)，直至完成所设计的各项接触压力测试。

这样，设置一个加热温度，可以获得试件在不同接触压力下的温度分布；改变加热温度，获得不同温度和接触压力下试件的温度分布。

图4 仪器安装过程Fig.4 The process of equipment installation

2.2 试件制备

生产过程中，井筒套管内过大的压力使水泥环发生塑性变形；内压减小时套管与水泥环收缩程度不同，在固井界面产生拉力；当拉力克服界面黏结力时，界面将会脱离而产生微环隙[13,18]。为模拟固井界面的微环隙，试件制备过程(图5)如下：

(1)制备直径25 mm、长度100 mm的人造岩心试件和套管试件。准备内径25.1 mm、长度150 mm的聚氯乙烯(PVC)塑料管作为水泥模具。

(2)将模子套在试件上部，倒入水泥浆(水固比为0.44)，捣拌多次以消除夹带空气对试件物性参数的影响；将试件和模子在330 K水浴环境中养护16 h；将水浴温度提升至355 K，PVC模子会因热膨胀而变形脱离。

(3)在热电偶位置将试件打孔。

(4)将固结好的试件在界面处小心拉开，形成岩心-水泥界面和套管-水泥界面。

(5)测试岩心-水泥试件组合的无侧限抗压强度为11.38 MPa、套管-水泥试件组合为15.39 MPa，即为实验设计接触压力的上限，如图6所示。

(6)测试水泥试件导热系数为0.699 0 W/(m·K)，岩心试件导热系数为1.655 4 W/(m·K)，套管试件导热系数为16.384 2 W/(m·K)。

这样就完成了岩心、套管、水泥试件的制备。

图5 水泥试件制作过程Fig.5 The manufacturing process of cement specimens

图6 组合试件的无侧限抗压强度测试Fig.6 Unconfined compressive strength test of composite specimens

2.3 实验测试的接触热阻

假设导热系数不随温度变化，则试件轴向上是恒定的传热过程，温度呈线性分布。

接触热阻R可根据牛顿冷却定律计算：

(10)

式(10)中：q为被加热试件和接受传热试件的平均热流，W/m2；THI和TCI是被加热试件和接受传热试件接触界面的温度，K。

平均热流q可由式(11)获得：

(11)

式(11)中：qH是被加热试件的热流，W/m2；qC是接受传热试件的热流，W/m2。λH和λC分别为两试件的导热系数，W/(m·K)。

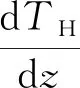
T=az+b

(12)

(13)

(14)

式中：i为热电偶测点的数量；T为试件温度，K；zi为第i个热电偶的位置，m；Ti为第i个热电偶测得的温度，K。

所用K型热电偶在273～670 K范围内会有0.5 K的漂移。本研究的温度在300～570 K，热电偶带来的最大相对误差为0.17%。相邻热电偶之间的距离为15 mm，绝对误差为0.1 mm，相对误差为0.67%。试件导热系数的相对测试误差估计为2.0%。按照误差传播规律，热流误差由温度、距离、导热系数的误差带来，最大为2.84%。因此，处理数据时，当计算的高温面和低温面热流差值超过2.84%时，应该舍弃这组数据。

根据热电偶的相对误差，界面处的温度跃变会有0.34%的相对误差；当不考虑热泄漏时，测试所得接触热阻的相对误差为3.18%。穿过绝缘材料的最大热流泄漏小于试件长度上热流的1.60%。因此，测试所得接触热阻的相对误差不超过4.78%。接触压力由重量和杠杆提供，相对误差分别为1.0%和0.2%。考虑试件传力和热膨胀中的分力，接触压力的相对误差估计为1.5%。

3 结果和讨论

3.1 实验结果与计算结果比较

实验测试并计算了同一环境温度下不同接触压力条件下水泥试件与岩心试件、套管试件的接触热阻。而运用理论计算方法[式(7)]时，首先需要确定两试件接触表面的温度和间隙宽度。表面温度可使用实验测试的结果。表面间距受接触压力的影响，由以下方法获得：

设定加热炉为某一温度，测试不同加载压力下两试件的接触热阻。实验设计组合如表1所示。由于环境、操作步骤是相同的，而测试温度和压力远未达到试件的弹塑性破坏条件，因此假设不同实验组次的试件表面间距和接触压力有相同的相关性。根据某一组测试的接触压力、接触热阻、表面温度，结合式(7)可以得到接触压力与表面间距的关系式；在其他组中，使用此关系式，得到理论计算的接触热阻，并与实验结果进行比较；如果理论结果与实验结果相近，则说明这个关系式是适用的。使用另一组测试数据得出接触压力与表面间距的关系式，而比较其他测试的结果。如果这些比较中，理论计算结果和实验结果相差不大，说明这个假设是成立的，而且接触热阻理论计算公式也是适用的。

表1 实验设计

图7(a)显示了测试(2)、(3)、(4)的实验结果与理论计算结果的比较，图7(b)显示了测试(1)、(2)、(4)的比较。可以看出，无论以测试(1)还是测试(3)拟合表面间距-接触压力关系，其他三组接触热阻的实验结果和理论计算结果偏差都在10%以内。考虑到接触热阻的实验测试误差、试件制作的差异性，这个可以接受。因此，前述推导的接触热阻理论计算式(7)是合理的。

图7 接触热阻的实验结果与理论计算结果比较Fig.7 Comparison of experimental results and theoretical calculation results of thermal contact resistance

3.2 井筒传热计算

以上述理论计算方法为基础，分析固井界面微环隙的接触热阻对井筒温度场预测精度的影响。稠油热采井中，井筒到地层的热量传递过程包括套管内壁到外壁的导热、水泥环内壁到外壁的导热以及地层内壁到远处的导热，如图8所示。

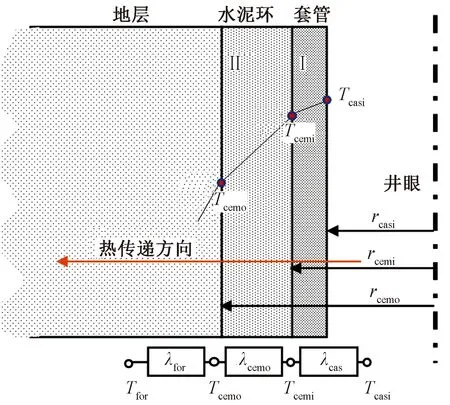
Ⅰ为第一固井界面，Ⅱ为第二固井界面；Tcasi为套管内壁温度，rcasi为内径，λcas为套管导热系数；Tcemi为水泥环内壁温度，Tcemo为外壁温度，rcemi为内径，rcemo为外径，λcem为水泥导热系数；Tfori为地层内壁温度，Tfori为远处温度，λfor为地层导热系数图8 井筒内地层-水泥环-套管传热示意图Fig.8 Schematic view of heat transfer of formation-cement sheath-casing in wellbore

由于地层的无限大特性，从井筒到地层的热量传递过程是非稳态的，井内不同位置处的温度和热流量随位置和时间而异。对任意深度的单位长度井段，可以将井筒到地层的传热过程简化为井筒到水泥环外缘的稳态传热和地层内的非稳态传热[23-24]。固井界面微环隙的表面温度可以通过试算的方法来确定，步骤如下：

(1)假设以套管内壁为基准的传热系数初始值kt0。

(2)计算套管至地层的传热量：

q1=2πrcasikt0(Tcasi-Tfor)

(15)

(3)根据热损失和热平衡，计算微环隙表面温度方法如下：

微环隙产生于水泥-地层界面时，水泥环外壁温度Tcemo和地层内壁温度Tfori计算如下：

Tcemo=Tcasi-q1(Rcas+Rcem)

(16)

Tfori=Tforo+q1Rfor

(17)

微环隙产生于套管-水泥环界面时，套管外壁温度Tcaso和水泥环内壁Tcemi计算如下：

Tcaso=Tcasi-q1Rcas

(18)

Tcemi=Tforo+q1(Rfor+Rcem)

(19)

套管和水泥环导热热阻分别为

(20)

(21)

根据Hasan公式[25]，地层导热热阻为

(22)

(23)

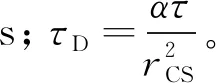
(4)将表面温度代入式(14)，考虑微环隙充满气体的情况，得到接触热阻RI。

(5)按式(24)重新计算总传热系数：

(24)

(6)若|kt1-kt0|较大，则以kt1作为初始值，重复上述步骤，直至差值达到最小。

这样，就可以获得固井界面微环隙的表面温度。

井筒各部分的计算参数如表2所示。

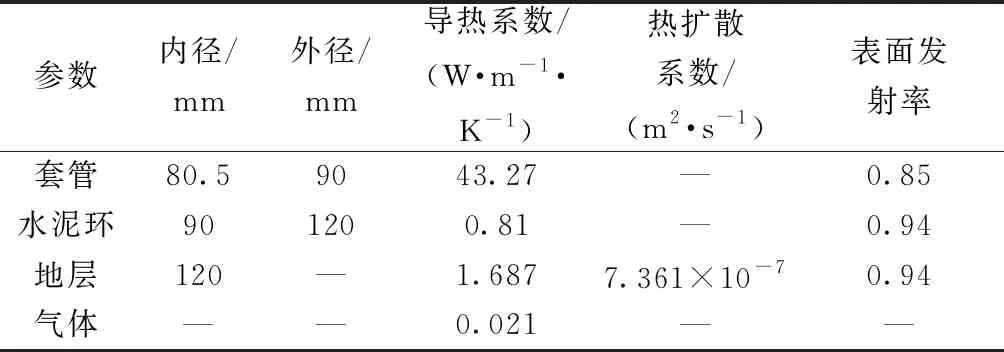
表2 井筒各部分物性参数

3.3 微环隙宽度对温度分布的影响

接触表面间距会影响接触热阻，进而影响表面温度。本算例设置套管内壁温度Tcemi=563.15 K，地层温度Tforo=305.15 K，注蒸汽时间为20 d，分析了固井界面微环隙宽度对壁面温度分布的影响。

图9(a)为套管-水泥环界面存在微环隙且宽度变化时的壁面温度分布，Tcaso和Tcemi为不考虑微环隙接触热阻时计算的套管外壁温度和水泥环内壁温度，RTcaso和RTcemi为考虑微环隙接触热阻时计算的套管外壁温度和水泥环内壁温度。可以看出，不考虑接触热阻时，Tcaso与Tcemi相等，且不随微环隙宽度而变化，相当于固井界面紧密接触的情况。考虑接触热阻时，RTcemi与Tcemi的温差随微环隙宽度的增加而不断增大，宽度为1 mm时温差达到14 K。

图9(b)为水泥环-地层界面存在微环隙且宽度变化时的壁面温度分布，Tcemo和Tfori为不考虑微环隙接触热阻时计算的水泥环外壁温度和地层内壁温度，RTcemo和RTfori为考虑微环隙接触热阻时计算的水泥环外壁温度和地层内壁温度。可以看出，不考虑接触热阻时，Tcemo和Tfori相等，也不随微环隙宽度而变化，相当于界面紧密接触的情况。考虑接触热阻时，RTcemo随微环隙宽度的增加而升高，宽度为1 mm时比Tcemo温度高3 K；RTfori随微环隙宽度的增加而降低，宽度为1 mm时比Tfori低12 K。

固井界面微环隙宽度越大，接触热阻越大，接触界面的壁面温差也越大。井筒温度场预测时忽略微环隙宽度变化导致的接触热阻变化，将使计算的水泥环外壁温度偏低，水泥环内壁温度和地层内壁温度有较大的偏高；微环隙越宽，温度偏差越大。

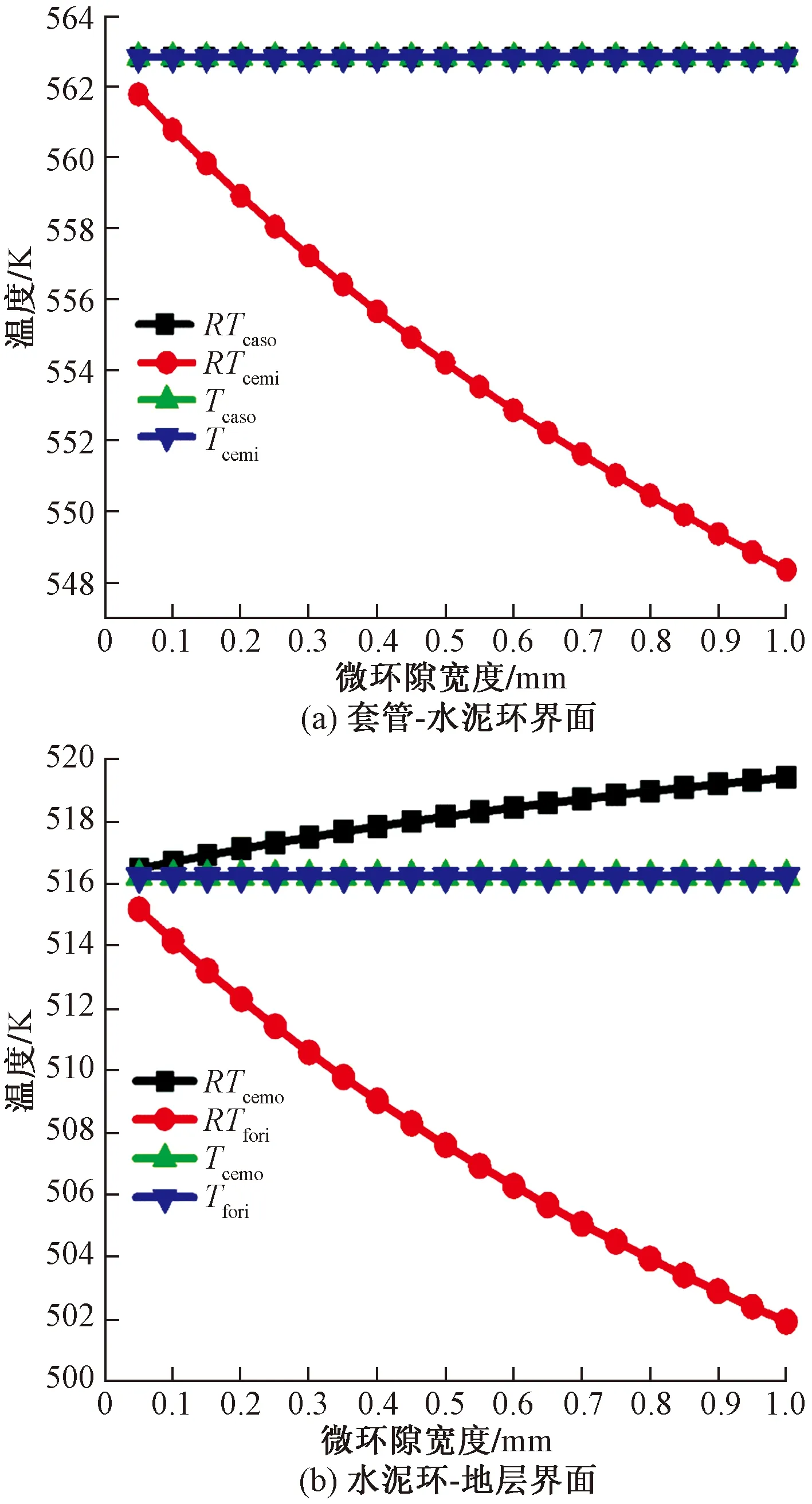
图9 微环隙宽度对表面温度预测的影响Fig.9 Effect of micro-annulus width on surface temperature prediction

3.4 注汽时间对温度分布的影响

随着井筒内注蒸汽时间增加，向地层的散热量也增加，引起温度场的不断变化。本算例设置固井界面微环隙宽度为0.05 mm，套管内壁温度Tcasi=563.15 K，地层温度Tforo=305.15 K，分析了井筒中注汽时间对壁面温度分布的影响。

图10(a)为套管-水泥环界面存在微环隙时的壁面温度分布。不考虑接触热阻时，Tcaso与Tcemi相等，且随注汽时间的增加缓慢升高。考虑接触热阻时，RTcemi低于Tcemi，偏差随注汽时间的增加而缓慢减小，注汽40 d后偏差由11.49 K减少为7.99 K。

图10(b)为水泥环-地层界面存在微环隙时的壁面温度分布。不考虑接触热阻时，Tcemo和Tfori相等，随着注汽时间的增加而升高。考虑接触热阻时，RTcemo高于Tcemo，偏差约3 K，且不随注汽时间增加而变化；RTfori低于Tfori，有约10 K的偏差，而不随注汽时间变化。

随着注汽时间的增加，井筒内各部分的温度在升高。忽略界面微环隙的接触热阻时，预测的水泥环外壁温度偏低，水泥环内壁和地层内壁温度偏高较多；随着注汽时间增加，温度偏差缓慢减小。

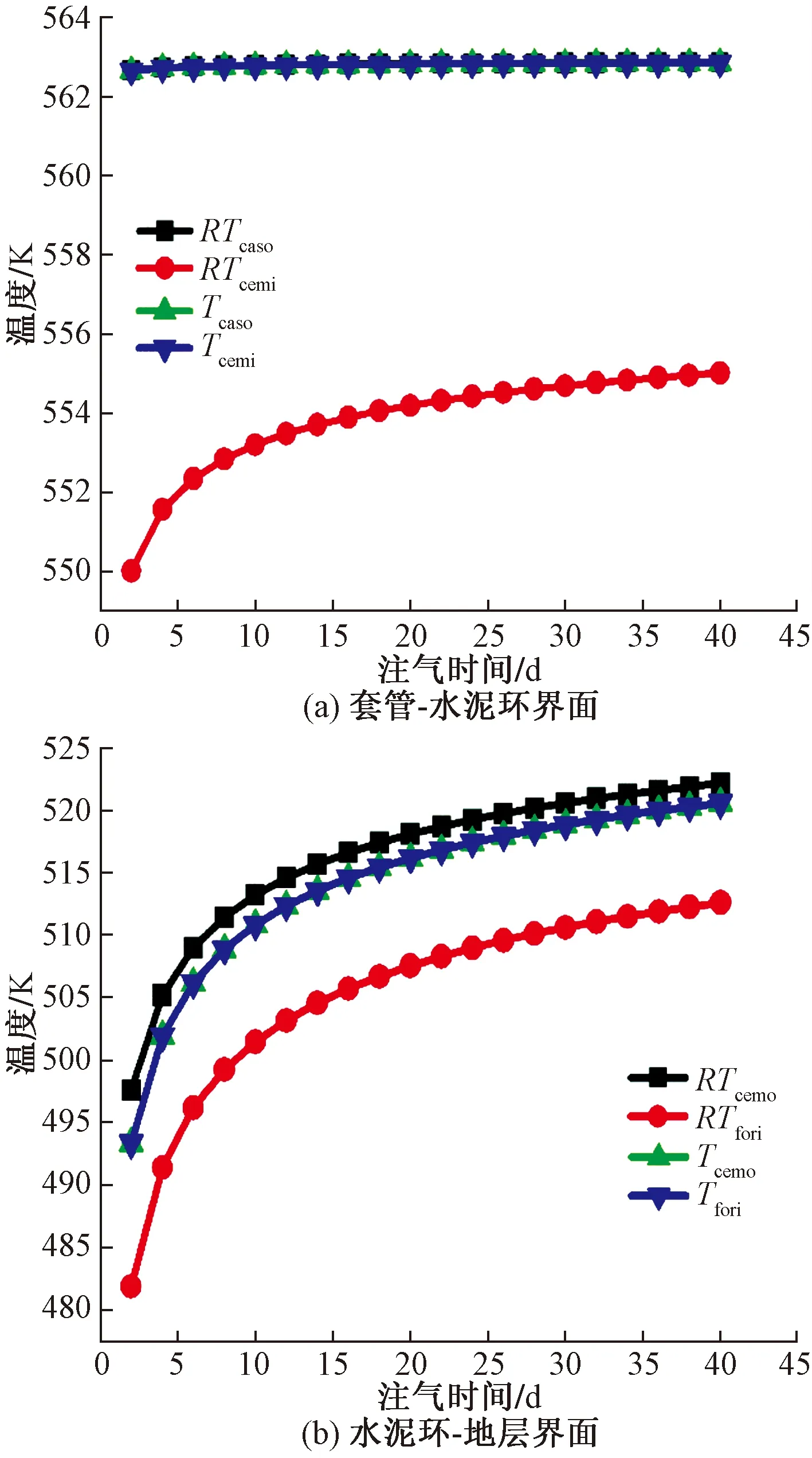
图10 注蒸汽时间对表面温度预测的影响Fig.10 Effect of steam injection time on surface temperature prediction

3.5 井筒深度对温度分布的影响

井筒内不同深度的地层温度不同，温度场分布也不同。本算例设置固井界面微环隙宽度0.05 mm，套管内壁温度Tcemi=563.15 K，注蒸汽时间为20 d，分析了井筒中不同地层温度时的壁面温度分布。

图11(a)为套管-水泥环界面存在微环隙时的壁面温度分布。不考虑接触热阻时，Tcaso与Tcemi相等，且随地层温度升高而缓慢升高。考虑接触热阻时，RTcaso没有变化；RTcemi低于Tcemi，偏差随地层温度升高而缓慢减小；地层温度升高95 K时，偏差减少了3 K。

图11(b)为水泥环-地层界面存在微环隙时的壁面温度分布。不考虑接触热阻时，Tcemo和Tfori相等，随地层温度升高而升高。考虑接触热阻时，RTcemo高于Tcemo，偏差较小，基本不随地层温度变化；RTfori低于Tfori，温差随地层温度升高而缓慢减小；地层温度升高95 K时，偏差减少了5 K。

随着地层温度升高，井筒内各部分的温度在升高。忽略界面微环隙的接触热阻时，预测的水泥环外壁温度偏低，水泥环内壁和地层内壁温度偏高较多；随着地层温度升高，温度偏差缓慢减小。

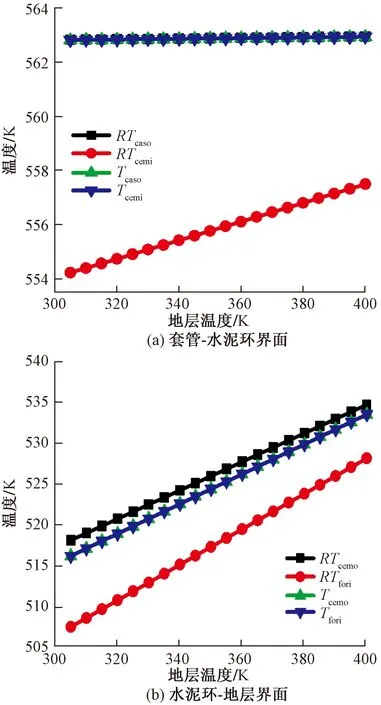
图11 地层温度对表面温度预测的影响Fig.11 Effect of formation temperature on surface temperature prediction

4 结论

的研究得到以下结论：

(1)推导了与接触表面温度和间距宽度相关的、适用于固井界面接触热阻计算的方法。

(2)将接触热阻应用到井筒温度场计算，发现固井界面微环隙宽度从0.05 mm增大到1 mm、注蒸汽时间从2 d增加到40 d、地层温度从305 K增加到400 K等情况下，预测井筒温度场时不考虑固井界面微环隙的接触热阻，将使计算的水泥环外壁温度有较小的偏低(约3 K)，而水泥环内壁温度和地层内壁温度有较大的偏高(约14 K)。表明预测井筒温度场时固井界面微环隙不可忽略。

(3)提出的实验仪器和试件制备方法，以及井筒径向传热计算方法，可以针对某口现场井，制作相应套管、水泥、地层试件进行测试，并计算井筒温度场。所得结果可以指导稠油热采井的套管和水泥环热应力分析，也可以指导地热开发中钻完井工程的钻井液和水泥浆耐高温性能设计。