Numerical study on the modulation of THz wave propagation by collisional microplasma photonic crystal

Shuqun WU(吴淑群),Yuxiu CHEN(陈玉秀),Minge LIU(刘敏格),Lu YANG(杨璐),Chaohai ZHANG(张潮海) and Shaobin LIU(刘少斌)

1 College of Automation Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,People’s Republic of China

2 College of Electronic and Information Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,People’s Republic of China

Abstract

Keywords:microplasma,plasma photonic crystal,terahertz wave,electron density

1.Introduction

Terahertz(THz)waves with a wavelength range of 30 μm to 3 mm have attracted considerable attention,due to their promising advanced applications,such as chemical spectroscopy[1],biomedical diagnostics[2],6 G communications[3],and astronomical observations[4].Photonic crystals(PCs)for THz wave modulation have been widely studied for over a decade[5].PCs possess photonic bandgaps(PBGs),within which the propagation of THz waves is not permitted,and which are usually used to confine and guide the desired propagating THz wave with a low degree of loss[6].Once a PC is developed,PBGs dependent on the structure of the PCs are barely capable of being tuned.To enhance the tunability of PBGs for THz wave modulation,plasma is introduced into the PCs,forming an artificial periodic structured composition of plasma and dielectrics,known as a plasma photonic crystal(PPC)[7-9].By electronically controlling the ignition and the physical properties of the plasma,the PBGs of the PPC become reconfigurable and tunable.Compared to other methods based on the external electric field[10],temperature[11],magnetic field[12],and pressure[13],the advantages of the PPC are the wide tunability of plasma permittivity from positive to negative values,and its rapid reconfiguration capability,facilitated by electronically switching the plasma on/off.These advantages of the PPC have been effectively demonstrated in relation to the modulation of the microwave propagation[14-18].

Microplasma is one promising candidate for the modulation of THz wave propagation in PPCs.In 2015,Askari et al[19]computationally analyzed the THz bandgap of a one-dimensional PPC with collision-free microplasma.They found that the width and the central frequency of the THz stopband gap are strongly dependent on the electron density and the plasma layer thickness.In 2016,PaneerChelvam et al[20]numerically modeled the interactions between a collisionless microdischarge cell and an electromagnetic wave at a frequency of 0.1 THz.It was revealed that due to the epsilon-zero critical density resonance,significant scattering,and the power deposition in the over-dense plasma is observed.In 2017,Yang et al[21]experimentally observed a narrowband attenuation at 157 GHz in a PPC composed of a microplasma jet array at atmospheric pressure.The narrow stopband width was 1 GHz and the maximum time-averaged attenuation of the electromagnetic wave was 5%,representing a surprising deviation from the simulated results.Subsequently,this group further demonstrated a possible application of a 3D PPC in relation to dynamic band-stop filters in the 120-170 GHz region[22].In these previous modeling results for a microplasma photonic crystal(MPPC),the collision frequency for momentum transfer between electrons and atoms or molecules in the PPC is considered to be negligible as compared to the incident wave frequency.However,this is not true for atmospheric pressure microplasmas,where the collision frequency attained is as high as several THz.Tian et al[23]reported that the uniformity of the collision frequency in high-temperature plasma for satellite reentry has a great impact on the THz absorption spectra.Therefore,collision frequency should be taken into consideration in PPC modeling at high pressure for the modulation of THz wave propagation.

In this work,the numerical modeling of a one-dimensional collisional MPPC is implemented by means of the transfer matrix method(TMM).In addition,the role of the collision frequency in plasma relative permittivity is theoretically analyzed.The effects of electron density,pressure,and plasma width on the THz band structure of MPPCs are also investigated.

2.Model and theory

2.1.Numerical model

Figure 1 shows a schematic of the one-dimensional collisional MPPC.Here,five quartz layers and four uniform microplasma layers are alternated and periodically located.The width(dq)and the dielectric constant(εq)of the quartz layer are 50 μm and 4.2,respectively.The width(dp)of the microplasma layer is 100 μm,which is variable in section 3.3.The lattice constant(d)of the MPPC is the sum of the widths of the quartz layer and the microplasma layer.The number of cycles of the MPPC is 4.A THz wave in transverse electromagnetic(TEM)mode is vertically incident to the MPPC.

Figure 1.Schematic of a one-dimensional collisional MPPC.Microplasma layer(red),quartz layer(grey).

2.2.Plasma relative permittivity

For non-magnetized plasma in weakly ionized gas,the expression for the plasma relative permittivity(εr)can be derived from the well-known Drude model[24]:

where ω,ωpe,and νmdenote the frequency of the incident electromagnetic wave,the plasma frequency,and the collision frequency for momentum transfer between electrons and atoms or molecules,respectively.In this case,ωpecan be obtained from the plasma equation in[25]:

where ne,e,me,and ε0represent the electron density in plasma,the electron charge,the electron mass,and the vacuum permittivity,respectively.Here,νmis proportional to the density of the gas,and is dependent on the electron temperature,which is given by[26]

where nmis the density of background gas(proportional to the gas pressure),p is the gas pressure,and Teis the electron temperature.Here,veis the thermal electron velocity,proportional to the square of the electron temperature,andσtris the momentum transfer collision cross section,which is also dependent on the electron temperature.For a gas pressure of 101 kPa(atmospheric pressure)and an electron temperature of 1 eV,the collision frequency is estimated to be 6.07×1012rad s−1.

Figure 2.Map of Re(εr)as a function of electromagnetic wave frequency(ω)and electron density.(a)Collision-free plasma,νm=0,(b)collisional plasma,νm=6.07×1012 rad s−1.

Based on equation(1),the value of the plasma relative permittivity is controllable on the complex plane by changing the plasma frequency and the collision frequency independently.Consequently,the attenuation and the phase shift of the THz waves can be varied.To clarify the role of collision frequency in this process,maps of the real part of the plasma relative permittivity,dependent on the electromagnetic wave frequency and the electron density for the collision-free plasma and the collisional plasma,are plotted in figure 2.For ω in the range of 0.1-0.5 THz,when the electron density increases from 1013cm−3to 1017cm−3,the Re(εr)decreases from 1 to a negative value.The minimums of Re(εr)are−804 for the collision-free plasma in figure 2(a)and−7.51 for the collisional plasma in figure 2(b),respectively.In other words,the addition of the collision frequency compensates for the reduction in Re(εr)for high electron density.

Figure 3 shows the values of the plasma relative permittivity,controlled by changing the gas pressure and the electron density independently.It is interesting to observe that both Im(εr)and Re(εr)decrease monotonically with the increase in electron density.When the gas pressure increases from 30 kPa to 202 kPa at the fixed electron density of 5×1016cm-3,the Im(εr)first decreases,reaching−8.04 at a gas pressure of 50.5 kPa,increasing as the gas pressure further increases.On the other hand,Re(εr)increases with an increase in the gas pressure.Therefore,both Im(εr)and Re(εr)can be varied by changing the electron density and gas pressure on demand.

To elucidate plasma-wave coupling based on plasma relative permittivity,a map of the loss tangent,defined by tanδ=Im(εr)/Re(εr),is plotted in figure 4.For an incident wave frequency of 0.1-0.5 THz,as the electron density increases from 1013cm-3to 1017cm-3,the tanδ decreases from 0 to a negative value,then abruptly reverses to a positive value.The transition region(region 1 in figure 4)corresponds to the value of the Re(εr)approaching to zero,which yieldsThis is useful for determining the electron density in plasma.

2.3.Microplasma photonic crystal

The MPPC consists of two dielectrics with different permittivities.One of these is microplasma.These two dielectrics are arranged alternately,as shown in figure 1.Due to the Bragger reflection,a photonic bandgap occurs in the MPPC,where electromagnetic wave transmission is forbidden.The relationship between the central wavelength of the bandgap,the refractive index,and the dimension parameters is given by:

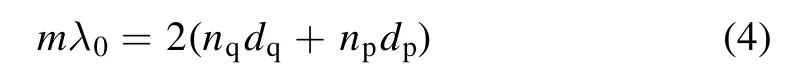
Figure 3.Real and imaginary parts of the plasma relative permittivity for different gas pressures and electron densities.The frequency of the incident electromagnetic wave is 0.5 THz.

where λ0is the central wavelength; m is an integer,which represents the formation of the periodic bandgap structure in the MPPC.Here,nqand npdenote the refractive indexes of quartz and plasma,respectively,and dqand dpare the widths of the quartz and the plasma,respectively.These refractive indexes are given by

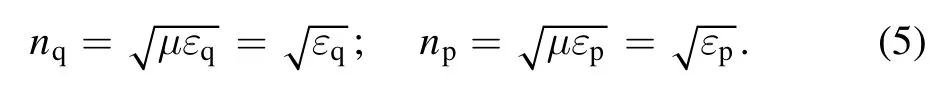
By substituting the corresponding central frequency of the bandgapf0=c/λ0,an expression related to the central frequency and the relative dielectric permittivity is obtained:

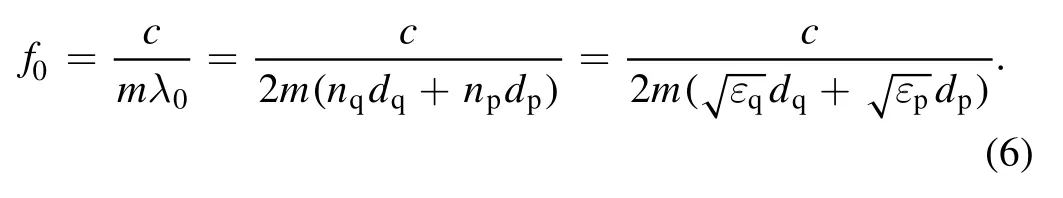
Figure 4.(a)Map showing the loss tangent as a function of incident wave frequency(ω)and electron density in collisional plasma.(b)The relationship between the loss tangent and the electron density at an incident wave frequency of 0.2 THz,corresponding to the dashed line in figure 4(a).The collision frequency is 6.07×1012 rad s−1.The grey strip(region 1)indicates that the value of Re(εr)approaches to zero.

Therefore,by tuning the microplasma permittivity and the dimensional parameters,the bandgap characteristics of the MPPC can be changed accordingly.

2.4.Transfer matrix method

The TMM is used to calculate the dispersion relation and the transmission of a vertically incident THz wave through the PPC,as shown in figure 1.This well-known method is based on the analytic solution of the 2D Maxwell’s wave equation,described in detail in[27].Therefore,only a brief introduction to this method is presented here.The electric field and the magnetic field at both sides of the Nth layer can be linked by the transfer matrix MNas follows:

where N equates to 4 in figure 1,and the transfer matrix MNis given by

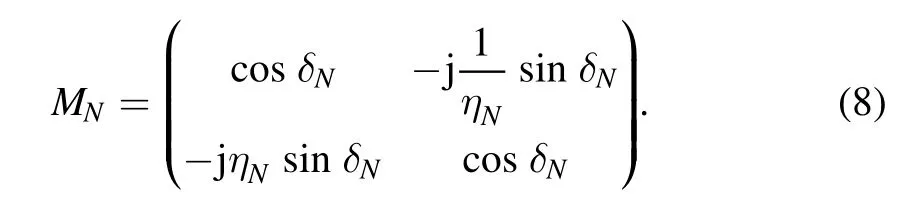
In this way,a single matrix can be defined for each dielectric layer;the relationship between the incident THz wave and the output THz wave can be therefore be calculated by

where M is the final transfer matrix for the one-dimensional collisional PPC with N dielectric layers.Here,A,B,C,and D are dependent on the permittivity of the dielectric layer and the dimensional parameters of the PPC.The power transmission coefficient of the THz wave and the dispersion relation are obtained from the final transfer matrix,given by

where η0and ηN+1denote the impedance of the THz wave at the left side and the right side of the PPC in figure 1,respectively,k denotes the wave number and δq,δp,ηq,and ηpare derived from

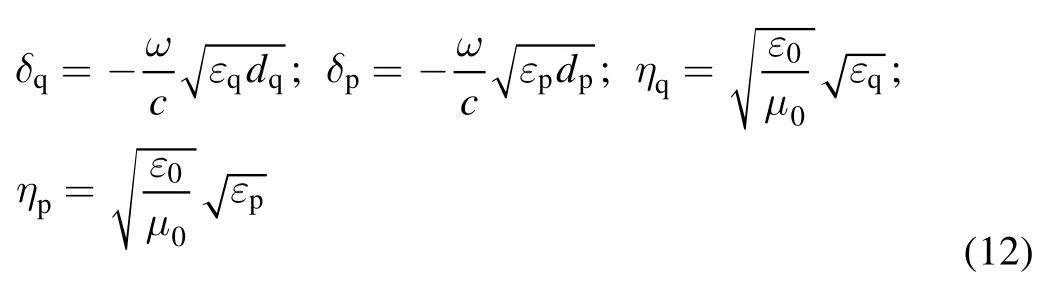
where c and μ0are the speed of light and the vacuum permeability,respectively.

3.Numerical results

3.1.Effects of collision frequency

To investigate the effects of the collision frequency,the THz transmission coefficient and the dispersion relation,both with and without consideration of the collision frequency,are calculated by the TMM,as shown in figure 5.Three THz stopbands at central frequencies of 0.85 THz,2.29 THz,and 3.75 THz are observed in both MPPCs,labeled as 1st BG,2nd BG,and 3rd BG.The bandwidths of these stopbands,defined by the full width at half maximum of the transmission coefficient,decrease as the central frequency increases.Moreover,a significant attenuation of the transmission coefficient is observed in the case of collisional microplasma.The lower the incident frequency,the larger the attenuation of the transmission coefficient will be.Similarly,when the collision frequency of 6.07×1012rad s−1(corresponding to the atmospheric pressure)is taken into account in the plasma relative permittivity,the dispersion relation is also significantly changed,indicating that the band structure of the PPC should be affected.

Given that the collision frequency is proportional to the gas pressure,we now investigate the effects of collision frequency on the THz transmission coefficient and the central frequency of the 1st BG via variations in the gas pressure.In figure 6(a),when the gas pressure increases,the transmission coefficient is shown to increase inside the 1st BG and on the left side of the 1st BG,but decreases at the right side of the 1st BG.On the other hand,the transmission coefficient around the 2nd BG and the 3rd BG decreases monotonically with the increase in gas pressure,as shown in figures 6(b)and(c).In addition,as the gas pressure increases from 50.5 kPa and 202 kPa,the central frequency shifts of the 1st BG,the 2nd BG,and the 3rd BG are 81 GHz,30.7 GHz,and 9.8 GHz,respectively.In figure 7,when the gas pressure increases from 50.5 kPa to 202 kPa,the central frequency of the 1st BG decreases monotonically from 0.871 THz to 0.79 THz.Therefore,the collision frequency has a great impact on the attenuation of the transmission coefficient and the band structure of the 1st BG for atmospheric pressure microplasmas.It should be noted that due to the strong attenuation of the THz wave propagation,the band structure of the 1st BG is severely distorted,resulting in the bandwidths for the 1st BG at different gas pressure being barely identifiable.

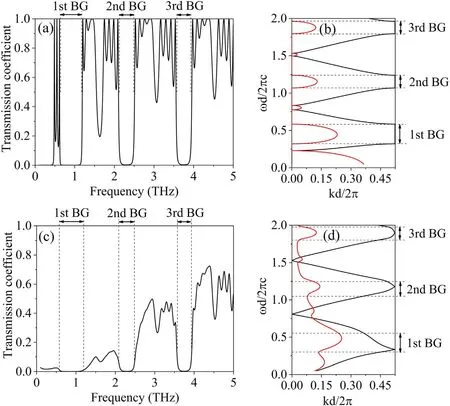
Figure 5.The THz transmission coefficient,and the dispersion relation of the MPPC for both collision-free and collisional microplasma.(a),(b)Collision-free microplasma,with an electron density of 1016 cm-3.(c),(d)Collisional microplasma,νm=6.07×1012 rad s−1,with an electron density of 1016 cm-3.

Figure 6.Transmission coefficients for(a)1st BG,(b)2nd BG,and(c)3rd BG as a function of the incident wave frequency at different gas pressures.The electron density is 1016 cm-3.

Figure 7.The central frequency of the 1st BG as a function of gas pressure.The electron density is 1016 cm-3.

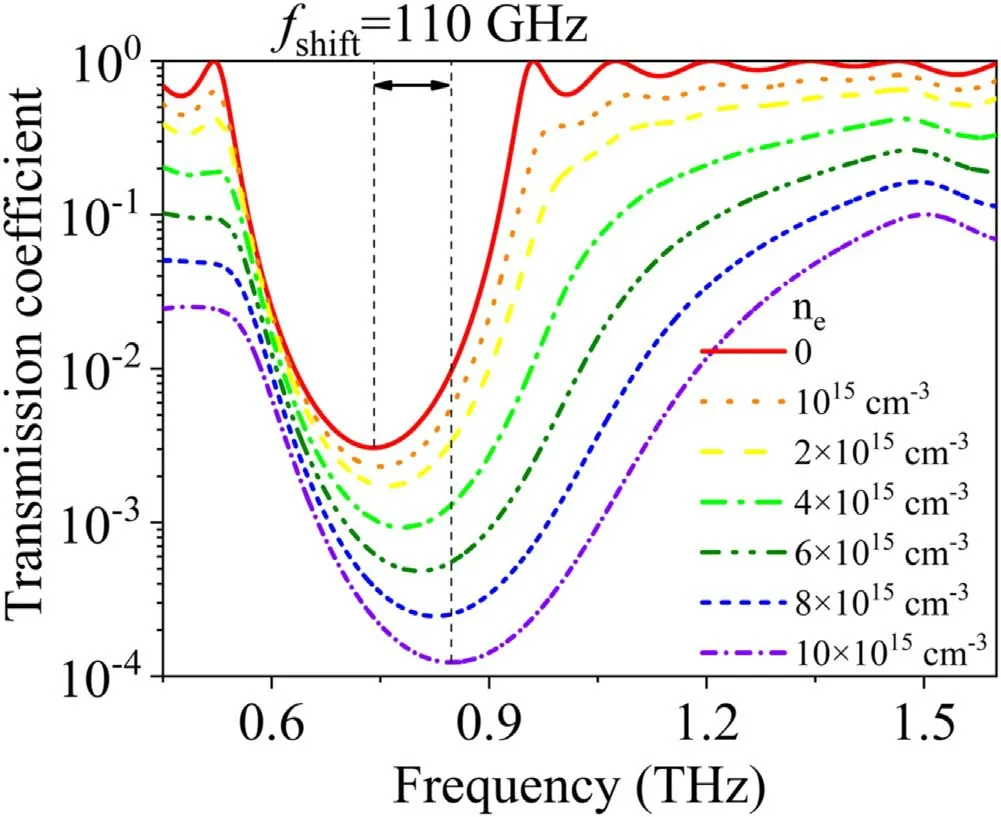
Figure 8.Transmission coefficient of the 1st BG as a function of incident wave frequency,with different electron densities.The collision frequency is 6.07×1012 rad s−1.An electron density of 0 represents vacuum.

3.2.Effects of electron density

Electron density is one of the key parameters in the study of plasma,and can be used to control the plasma’s relative permittivity by means of plasma frequency,as shown in equation(2).Figure 8 shows the transmission coefficient in the 1st BG as a function of electron density.When the electron density increases from 0 to 1016cm-3,the shift of the central frequency of the 1st BG is 110 GHz,and the transmission coefficient around the 1st BG decreases by at least one order of magnitude over all bandwidths.Figure 9 shows the relationship between the electron density,the central frequency,and the bandwidth of the 1st BG.When the electron density increases from 1013cm-3to 1015cm-3,both the central frequency and the bandwidth of the 1st BG remain almost unchanged at around 0.74 THz and 0.42 THz,respectively.However,as the electron density further increases from 1015cm-3to 1016cm-3,both the central frequency and the bandwidth increase significantly,up to 0.85 THz and 0.62 THz,respectively.In figure 10,as the electron density increases from 0 to 1016cm−3,the shifts of the central frequencies of the 2nd BG and the 3rd BG are 67 GHz and 53 GHz,respectively.The transmission coefficients at the central frequencies in the 2nd BG and the 3rd BG are attenuated by less than three times.In summation,the higher the central frequency of the THz stopband,the less significant the impact caused by the electron density will be.In addition,it should be pointed out that electron density has a minor impact on the THz band structure of the MPPC if the electron density is less than 1015cm-3.

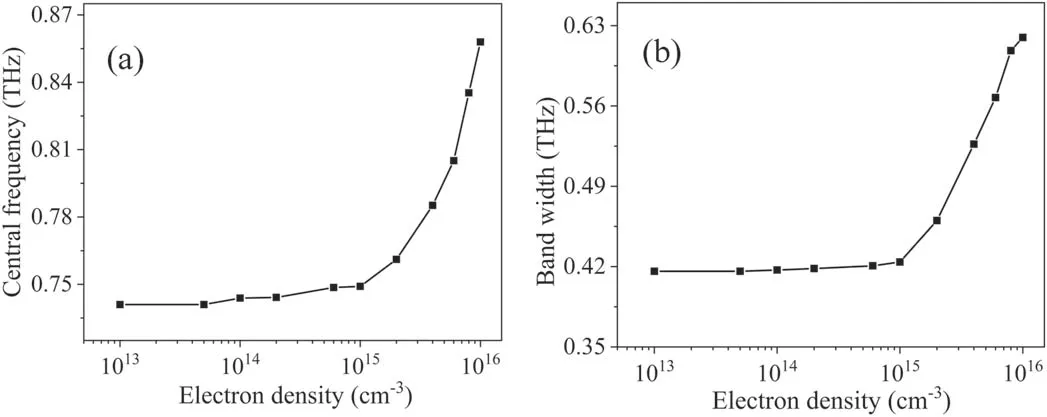
Figure 9.Central frequency and bandwidth of the 1st BG as a function of electron density.Here,the collision frequency is 6.07×1012 rad s−1.

3.3.Effects of plasma width

As illustrated by the results above,the electron density required for the THz wave modulation is greater than 1015cm−3.It is not easy to develop such a low-temperature,high electron-density plasma at high pressure.The recent development of microplasmas generated inside a capillary or a cavity is anticipated to meet these strict requirements[28-30].However,the dimensional parameters of microplasmas are strictly limited,and have a significant influence on the electron density of the microplasmas[28,31].It is therefore essential to investigate the effects of plasma width on the THz transmission coefficients of MPPCs.In figure 11,when the plasma width increases from 50 μm to 70 μm(i.e.larger lattice constant),the central frequencies for the 1st,2nd,and 3rd BGs are shifted toward a low frequency,and the transmission coefficients duly decrease.

Figure 10.Transmission coefficients for(a)2nd BG and(b)3rd BG as a function of incident wave frequency,with different electron densities.The collision frequency for both is 6.07×1012 rad s−1.

4.Discussion

By introducing microplasma into the photonic crystal,a widely tunable MPPC is obtained.For example,as the electron density of the microplasma increases from 1015cm-3to 1016cm-3,the central frequency of the 1st BG shifts toward high frequency by 110 GHz,and the bandwidth of the 1st BG increases by about 200 GHz.The tunable range of the band structure caused by microplasma is much greater than that by controlling the temperature or the electric field to change the conductivity of the metamaterial[10,11].This method of THz wave modulation is probably useful in chemical spectroscopy[1],biomedical diagnostics[2],and astronomical observations[4].

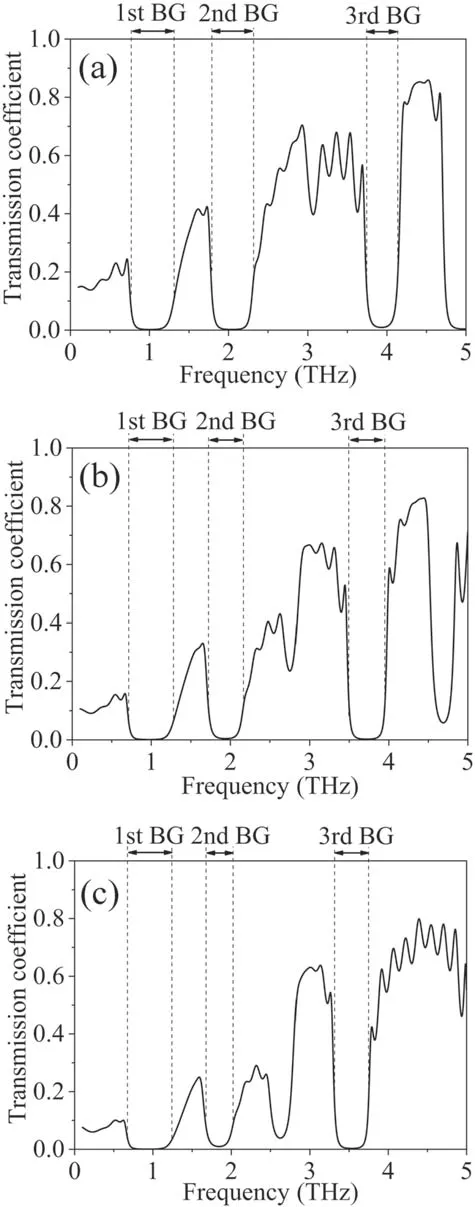
Figure 11.The THz transmission coefficients of the MPPCs with different plasma widths.(a)50 μm,(b)60 μm,and(c)70 μm.The width of the quartz remains constant.Here,the collision frequency is 6.07×1012 rad s−1,and the electron density is 1016 cm-3.

4.1.The mechanism of THz wave modulation

With regard to the modulation of the central frequency of the THz stopband,based on equation(6),the central frequency of the stopbands in the MPPC is related to the relative permittivity of the microplasma.As shown in equations(1)and(2),the relative permittivity of the microplasma is dependent on electron density and collision frequency,which are proportional to the gas pressure.The relative permittivity of the microplasma is a complex,in contrast to the permittivity of quartz.The imaginary component of plasma permittivity represents the energy dissipation of the electromagnetic wave,and the real part of the plasma permittivity is related to the band structure of the MPPC[26].In order to clarify the relationship between gas pressure,electron density,and the central frequency of the THz stopband,the imaginary component of the plasma permittivity is neglected.By substituting equations(1)and(2)into equation(6),the central frequency can be given by

Figure 12.Theoretical central frequency of the 1st BG as a function of(a)gas pressure,and(b)electron density.

With the knowledge of the values of εq,dq,dp,m,e,me,ε0,and c,the relationship between the central frequency of the 1st BG,its electron density,and the gas pressure can be calculated theoretically,as shown in figure 12.As the gas pressure increases from 50.5 kPa to 202 kPa,the central frequency of the first THz stopband decreases from 0.95 THz to 0.78 THz,which is slightly higher than that for TMM in figure 7.When the electron density increases from 1013cm-3to 1016cm-3,the central frequency of the first THz stopband increases from 0.74 THz to 0.86 THz,which is in good agreement with the results calculated via TMM in figure 9(a).

With regard to the modulation of the bandwidth of the THz stopband,the bandwidth is usually dependent on the ratio of the refractive index of these two dielectrics,and their dimensional parameters.In photonic crystals,the higher the ratio of the refractive index(nq/np),the larger the bandwidth will be[32].The refractive index of the plasma is determined by the plasma permittivity,expressed as[26]:

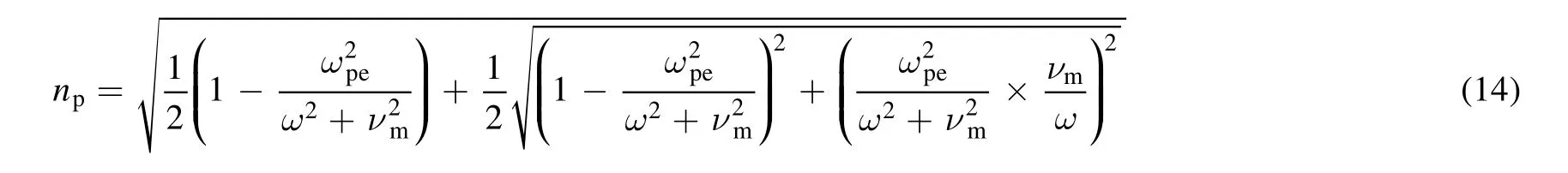
Similarly,with a fixed collision frequency of 6.07×1012rad s−1,the relationship between the refractive index of the plasma and the electron density in relation to different incident wave frequencies is calculated theoretically.Figure 13 indicates the way in which,as the electron density increases from 1013cm-3to 1015cm−3,the refractive index of the plasma decreases slowly from 1.0 to 0.97 for a wave frequency of 0.8 THz,resulting in an almost constant ratio of the refractive index of these two dielectrics.However,when the electron density further increases up to 1016cm−3,the refractive index of the plasma decreases significantly,from 0.97 to 0.8,leading to a rapid increase in nq/npvalues,and therefore an increase in the bandwidth of the stopband.These results are consistent with the numerical results calculated by TMM in figure 9(b).Therefore,by tuning the electron density and the gas pressure,the permittivity of the microplasma can be varied,resulting in the modulation of the structure of the THz stopbands in MPPCs.

Figure 13.Theoretical refractive index of plasma as a function of electron density,with different incident wave frequencies.

4.2.The mechanism of THz wave attenuation

From the perspective of electromagnetic wave propagation,collisional plasma is a dissipative medium,which leads to the attenuation of THz wave propagation.This is because the electrons gain energy from the electric field of the THz wave,and then transfer it to the molecules or atoms through frequent elastic collisions[33].The absorption index is given by[26]:

The absorption index is therefore shown to be greatly dependent on the third term,,corresponding to the imaginary part of the plasma permittivity.For electron densities of 1015cm-3and 1016cm-3,the plasma frequencies are 0.28 THz and 0.9 THz,respectively.The collision frequency at atmospheric pressure is 0.96 THz.On one hand,when ω≫νmand ω≫ωpe,equation(15)can be simplified as follows:

Therefore,the higher the electron density and the collision frequency are,the larger the absorption index is,and the stronger the attenuation of THz wave propagation will be.This exact phenomenon can be observed for both the 2nd and 3rd BGs in figures 6(b)and(c),and figure 10.On the other hand,the frequency of the incident THz wave in the 1st BG is close to the plasma frequency,but less than the collision frequency at high pressure.By assuming ω≪νm,the equation(15)can be simplified as follows:

It is therefore clear that an increase in collision frequency leads to a decrease in the absorption index,resulting in a weak attenuation of THz wave propagation.This is why a higher transmission coefficient in the 1st BG is obtained as the gas pressure increases.From the perspective view of plasma physics,the higher the gas pressure is,the shorter the mean free path will be.For ω≪νm,several elastic collisions between electrons and atoms or molecules occur during one period of THz wave.When these collisions become more frequent,it becomes increasingly difficult for the electrons to gain energy from the electric field,due to the shorter mean free path.

For microplasma generated at atmospheric pressure,the collision frequency for momentum transfer between electrons and atoms or molecules is in the THz range,which cannot be neglected in terms of the plasma’s relative permittivity.In this work,taking the collision frequency into account,the characteristics of the THz band structure of the MPPC are investigated for the first time.In figure 5,taking into account the collision frequency at 101 kPa,the THz transmission coefficient and the dispersion relation of the MPPC make a difference.Further investigation shows that collision frequency and electron density have a great impact on both the transmission coefficient and the band structure of the first THz stopband for atmospheric pressure microplasmas.This differs from the results in previous research on the subject of microwave attenuation due to low-pressure volume plasma[34,35],where the collision frequency has a negligible effect on the band structure of the PPC in the microwave range,but a great impact on the attenuation of microwave propagation in plasma.In low-pressure volume plasma[34,35],since the collision frequency is negligible as compared to the incident wave frequency,the real part of the plasma relative permittivity is almost independent of the collision frequency,and the imaginary part of the plasma relative permittivity is proportional to the collision frequency,based on equation(1).

4.3.Microplasma for the modulation of THz wave

With regard to the characteristics of plasma employed for the modulation of a THz wave,it is interesting to note that in order to have a significant impact on the band structure of the MPPC,the electron density of the plasma must be at least 1015cm−3.It is almost impossible to realize such low-temperature plasma with high electron density at low pressure.However,several reported methods,based on microdischarge,nanosecond pulsed discharge,RF discharge,or microwave discharge represent several possible pathways to generating high-ionized plasma at atmospheric pressure.Our recent research has demonstrated atmospheric pressure microplasma sources generated inside capillaries,with an electron density of 1015-1017cm-3[28,31,36].These results suggest the possibility of achieving wide tunability of the THz band structure in MPPCs.Moreover,in relation to plasma width,simulation results show that the stopband structure of the plasma photonic crystal exists for plasma widths of tens of micrometers,disappearing as the plasma width further increases up to 800 micrometers.This indicates that the characteristic size of the plasma should ideally be tens to hundreds of micrometers in order to achieve successful modulation of a THz wave.In other words,microplasma at atmospheric pressure is well-suited to the modulation of THz waves.

In addition,although the high gas pressure and high electron density of the MPPC can significantly alter the bandwidth and the central frequency of THz stopbands,there is a concomitant sizeable reduction in the transmission coefficient of the THz wave,as shown in figures 6(a)and 8.For example,the transmission coefficient decreases by at least one order of magnitude for an electron density increase of up to 1016cm−3,which may be not appropriate for the modulation of THz waves in real applications.Therefore,taking full account of the attenuation and modulation of THz wave propagation,the ideal electron density of microplasma at atmospheric pressure is suggested to be in the range from 1×1015-6×1015cm-3,where the attenuation of the THz wave propagation by the MPPC is then less than 10 dB.

5.Conclusion

Taking collision frequency into consideration,the THz band structure and the transmission characteristics of a onedimensional MPPC are simulated via TMM.At high pressure,both the electron density and the collision frequency for momentum transfer between electrons and atoms or molecules have a significant impact on the attenuation of the THz wave and the THz band structure,by altering the plasma permittivity.On increasing the electron density from 1015cm-3to 1016cm-3,the central frequency of the 1st BG shifts toward high frequency by 110 GHz,and the bandwidth of the 1st BG increases by about 200 GHz,far higher than the results achieved by previously recorded methods[10-13].Moreover,as the gas pressure increases,the transmission coefficient increases at low frequencies in the incident THz wave,but decreases at higher frequencies of incident THz wave,where ω≫νmand ω≫ωpe.On the other hand,the transmission coefficient decreases monotonically with an increase in the electron density.In addition,to achieve wide tunability of the THz stopbands of MPPCs,the electron density must be as high as 1015cm−3,and the ideal feature size of the plasma should be submillimeter.This study indicates that high electron-density microplasma at atmospheric pressure is likely to be suitable for the modulation of THz wave propagation in MPPCs.

Acknowledgments

This work was supported by National Natural Science Foundation of China(No.51977110).