打磨作业场所多尘源耦合扩散规律研究

蒋仲安 张国梁 陈建武 杨斌 陈记合

摘   要：为了改善移动打磨作业场所粉尘浓度超标的现状，以中车长客打磨车间为研究背景，利用高斯扩散模型，建立非稳态单尘源粉尘扩散模型，采用线性回归方法，研究多尘源耦合扩散规律;根据实验测定的不同高度单点和多点打磨的粉尘浓度，结合气溶胶粒子的运动方程和梯度下降法，求解出粒子扩散系数和多尘源耦合系数. 将得到的粉尘扩散模型与对照实验进行验证，结果表明，多点打磨在两个打磨点中间向前一定距离处会出现聚集点，且不同高度聚集点位置不同;多点打磨空间粉尘浓度是单点打磨的2～3倍，且最大值高达45.73 mg/m3，远高于国家卫生标准;多尘源打磨作业粉尘扩散模型平均误差为14.67%，具有一定可靠性，可用于后续对打磨车间粉尘防护技术和空间优化布置的研究.

关键词：打磨场所;扩散模型;多尘源耦合;浓度分布;扩散系数;梯度下降法

中图分类号：X964                                文献标志码：A

Study on Coupling Diffusion Law of

Multi-dust Sources in Grinding Workplace

JIANG Zhongan1?，ZHANG Guoliang1，CHEN Jianwu1，2，YANG Bin1，2，CHEN Jihe1

（1. School of Civil and Resource Engineering，University of Science and Technology Beijing，Beijing 100083，China;

2. China Academy of Safety Science and Technology，Beijing 100029，China）

Abstract：To improve the current situation of excessive dust concentration in the places of mobile grinding， this thesis， based on the research background of CRCC Changke grinding workshop， establishes an unsteady single-dust diffusion model with the guidance of Gaussian diffusion model. The liner regression method is used to investigate the rules on the diffusion of multi-point dust interactions. It makes a comparative analysis of the data on the dust concentration in single point or multi points， which varies with the height. And combined with the equation for Groundwater Flow and the method of Gradient Decent， it finds out the coefficient of particle diffusion and multipoint dust interactions. The result shows that a gathering point can form between any two grinding points and it may also change with the altitude. The dust concentration of the multi-point grinding is 2 to 3 times of the single point grinding， and the maximum value is up to 45.73 mg/m3，which is higher than the standard of the state health. The average error of the dust diffusion model is verified as 14.67%， and it can be used for subsequent research on the protection technology from the dust and workshop spatial structure.

Key words：grinding workplace;diffusion model;multi-dust source coupling;concentration distribution;diffusion coefficient;gradient descent

打磨作業是工业生产中常见的作业方式，其产生的粉尘、噪声以及手柄的振动等职业危害除了影响生产效率和设备的使用寿命，还会对人体产生损伤，长时间接触更会产生职业病，特别是打磨产生的粉尘，扩散到空间中，会导致严重污染. 为了对打磨作业产生的粉尘进行治理，特对其扩散规律进行研究.

粉尘扩散规律基于高斯扩散模型，对气-固或气-固-液之间耦合关系进行研究，常见的数学研究方法有欧拉、拉格朗日法等[1]，也可通过数值模拟[2-5]（Fluent、Matlab）进行研究，将数学模型内嵌到软件中使用. 近些年，国内外许多学者对粉尘的扩散规律进行实验和模拟研究. Zhao等[5-6]分析影响室内颗粒物沉降的几个影响因子，并对欧拉法和拉格朗日法模拟的可靠性进行研究; Zhao等[7]在湍流模式下建立粉尘分布和悬浮模型，并用CFD-DPM进行模拟;李明等[8-9]利用费克扩散定律，建立了瞬时点尘源在不同流体下的扩散模型，并采用Matlab对其进行可视化处理;蒋仲安等[10]对综采工作面移架和割煤过程的呼吸性粉尘扩散和耦合规律进行研究，得出了求解扩散系数的有效方法;王洪胜等[11]采用Fluent对井下工作面多尘源的粉尘扩散进行数值模拟和实测，为工作面防尘提供了有效技术支持;蒋仲安等[12-13]在高斯扩散模型基础上，建立移动式打磨作业粉尘扩散分布数学模型，利用Python设计了基于该模型的可视化仿真程序;黄武[14]对打磨产生的粉尘颗粒的微观特性进行了研究.

本文针对打磨车间的粉尘扩散，利用高斯扩散规律，对现场多尘源粉尘扩散模型进行研究，并利用实验数据求解未知参数，再与实测值进行对比验证，从而得到打磨作业的粒子扩散模型.

1   打磨车间粉尘扩散的数学模型

1.1   静止介质中非稳态单尘源扩散模型

悬浮于空气中或其他介质中的微粒受到介质粒子的碰撞，进行布朗运动. 大颗粒粉尘在重力的作用下会沉降到地面;小颗粒粉尘由于布朗运动会进行扩散迁移，由粒子浓度高的区域迁移到浓度低的区域，迁移过程还伴随着粒子的凝聚和沉降，即颗粒之间由于布朗运动相互碰撞而发生凝并，形成大颗粒并最终沉降.

目前，对于粉尘扩散迁移模型的研究，主要基于菲克扩散定律：在各项同性的介质中，穿过单位截面积的扩散物质的迁移速度与该截面浓度梯度成正比，即菲克第一扩散定律.

式中：F为单位时间内通过单位面积的粒子质量，g/（m2·s）;D为扩散系数，m2/s，某些情况下，D为常数;c为扩散物的质量浓度，g/m3;x为扩散距离，m.

菲克第一扩散定律是基于稳态得出的结果，即F和c不随时间变化，而实际上粒子扩散运动多为非稳态扩散，F是时间与空间的函数.

对于单位体积微元，中心坐标为O（x，y，z），边长分别为2dx、2dy、2dz，扩散物资的质量浓度为c，则从面ABCD流入到微元体的扩散物质的量为4dydz（Fx-dx），其中Fx是微元体中心O沿x方向的扩散通量，dx为从中心点到面ABCD沿x方向扩散通量的下降值;同理，从面A′B′C′D′流出的扩散物质的量为4dydz（Fx + dx）. 所以在这两个面之间，微元体内扩散物质的增量为-8dxdydz，其他两组对应面的增量同理;而微元体内总的质量变化为8dxdydz，得到式（2）为：

打磨作业车间属于半封闭状态，无明显的风流流动. 当忽略人员和运输设备运动引起的扰动风流时，打磨作业产生的粉尘颗粒可以看做是在静止的空气中扩散. 假设在点（x，y，z）处存在一个连续作业的打磨点（尘源），产尘量连续且均匀，单位时间的产尘量为M，扩散系数D为常数，将式（1）代入式（2），可得粉尘随时间和空间的扩散模型，即：

1.2   打磨车间多尘源耦合粉尘扩散模型

对于打磨作业，若设定打磨点为坐标原点，且尘源属于连续稳定产尘，c/t = 0，则可求得粉尘随时空变化的微分方程的一般解.

式中：K为常数，由边界条件确定. 扩散到空间的粉尘满足质量守恒定律且源强均匀连续，所以以源点为中心的任意一立方体内的粉尘向外的迁移量为常数，等于源点的粉尘发散量，即：

中车长客打磨车间的实际布置如图2所示，每個打磨台之间的距离为ΔX和ΔY，打磨点距地高度为H. 由高斯扩散模型可知，车间地面、四周墙体和屋顶都会对粉尘的扩散产生影响，但由于车间范围较大，四周的墙体和屋顶的影响可忽略，只需要考虑地面对粉尘的影响.

为便于研究，先对A、B、C三个小件打磨点进行讨论. 以B点为原点，建立坐标系，研究打磨车间单尘源的扩散规律. 即地面看做是镜面，对粉尘具有反射作用，对应的存在一个虚拟点源，空间内某点P（x，y，z）的粉尘质量浓度，可以看做是两部分的叠加：一部分是地面不存在时，实际尘源扩散到该点的粉尘，另一部分由于地面反射到该点的粉尘，也可以看做是位于点（0，0，H）和点（0，0，-H）的两个尘源共同作用的结果.

实源在空间内某点P产生的粉尘质量浓度为：

虚源在空间内P点产生的粉尘质量浓度为：

则B打磨点产生的粉尘，扩散到P点的实际质量浓度为实源和虚源的叠加和，即：

同理，A、C打磨台连续作业产生的粉尘扩散到P点的实际质量浓度分别为：

固体粒子受重力影响，在扩散过程中并不是一直在空气中运动，存在向下沉降的现象，特别是大颗粒，在不考虑地面的反射作用时，对上述距地面高度为H的源点的扩散公式进行修正，根据最终的沉降速度vt和扩散时间t，得到B打磨点粉尘扩散质量浓度的计算公式，如式（13），A打磨点和C打磨点同理可得.

假设打磨作业多尘源耦合可用线性模型表示，即P点粉尘质量浓度的估计值与3个产尘点在P点的粉尘质量浓度满足线性关系，其多元线性回归的基本模型为：

式中：k0、k1、k2、k3为多尘源耦合系数;c（x，y，z，t）为t时刻，在多个连续尘源作用下P点的粉尘质量浓度.

2   打磨作业粉尘扩散的实验研究

2.1   打磨实验模型设计

根据车间的实际情况，对打磨作业粉尘扩散规律进行实验研究. 由于打磨工具、作业场所和作业方式的不同，空间流场和切削粉尘初动能存在差异，最终粉尘的空间质量浓度分布存在差异. 实验针对与建立的理论模型相似的典型作业场所和作业方式的粉尘扩散规律进行研究，连续打磨作业时，控制打磨参数保持不变，认为尘源连续且均匀产尘.

实验布置如图3所示，共设置3个打磨点，A（-1.6，0，0）、B（0，0，0）、C（1.6，0，0），每个打磨点选取两个不同高度的粉尘质量浓度待测面，分别为打磨点高度（z=0）和呼吸带高度（z=0.7）;尘源附近每个平面（XY平面）的测点布置如图4所示，采用CCZ（20）-A型粉尘采样仪进行质量浓度测定，由于短时间打磨作业，空间内粉尘不稳定，所以每次打磨时间持续40 min，并进行两组重复实验，其中一组是对照实验，用于降低实验误差.

2.2   单点打磨作业的粉尘浓度测定结果及分析

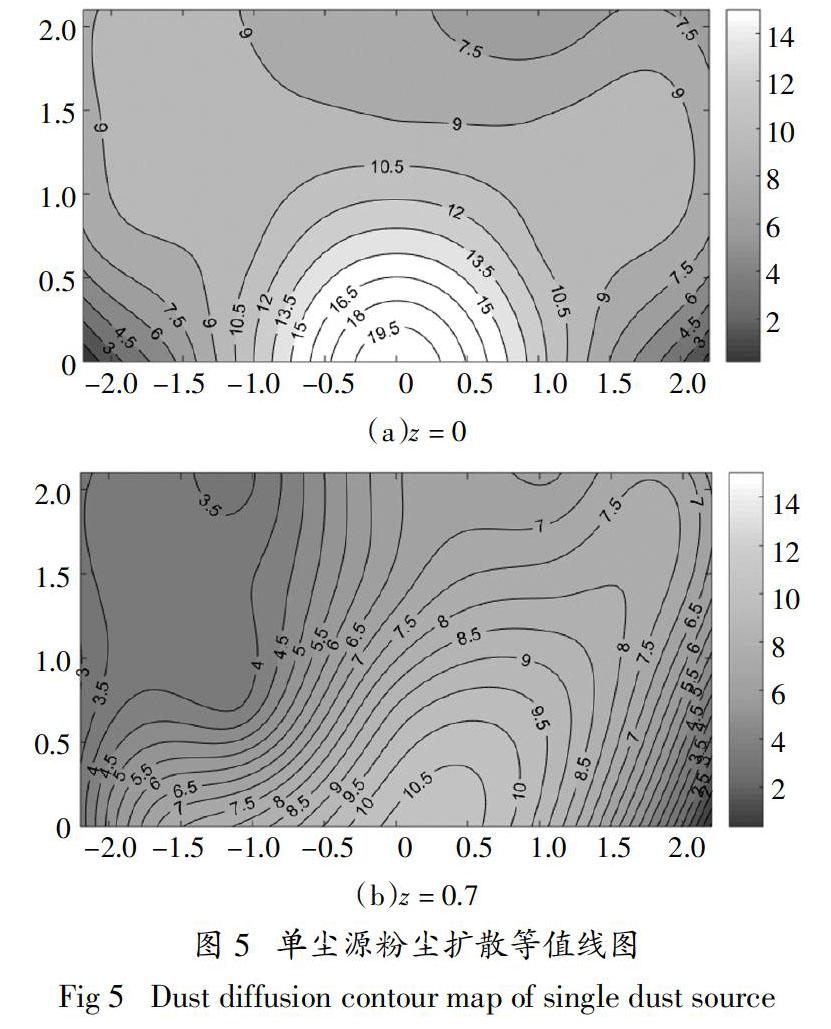
当只有B工作台进行作业时，打磨40 min，用采样仪测定后20 min的平均粉尘质量浓度，用Matlab对实验数据进行二维3次插值处理，得到的打磨点高度和呼吸带高度粉尘质量浓度分布等值线图如图5所示.

由图5可知：

1）粉尘由打磨点向四周逐渐扩散，打磨点处的粉尘质量浓度最高，向外逐渐递减;相同距离下，递减的幅度越来越小;距离打磨点越近，粉尘扩散越均匀，等值线越接近半圆形. 在点（0，0，0）位置，粉尘质量浓度达20.9 mg/m3，在点（0，0，0.7）位置（呼吸带高度），粉尘质量浓度依旧高达10.67 mg/m3，明显高于规程规定值.

2）在z = 0平面靠近打磨点位置处，粉尘质量浓度分布呈半圆形，继续向外会出现一个放射状;产生的粉尘扩散区域主要位于打磨点前方“中线左右45°”范围内，且在两个底角处浓度最低，与前面理论研究的粉尘扩散吻合.

3）在呼吸带高度（z = 0.7）处，打磨点正上方的粉尘质量浓度最高，向外逐渐降低;整体粉尘质量浓度较z = 0平面有较大下降，但在作业位置处的粉尘质量浓度依然超过规定值，所以长时间打磨作业必须佩戴防护设施. 在等值线图的右前方45°处存在“尖刺”，离打磨点越远越明显，这是由于实验时以砂轮左侧为打磨点，倾斜接触钢板，导致产生的部分粉尘和火花向右前方倾斜飞出，出现局部粉尘质量浓度增大的现象.

2.3   多点同时作业的粉尘浓度测定结果及分析

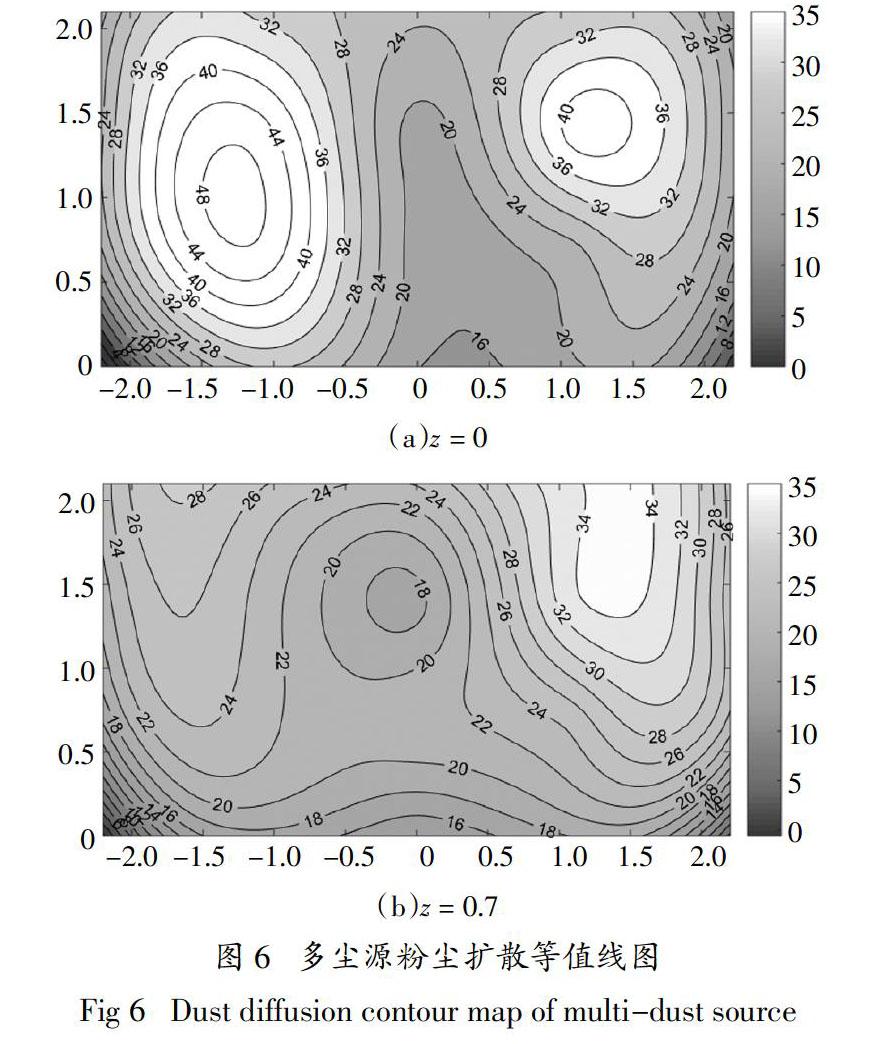
当A、B、C 3个打磨点同时作业，共打磨40 min，用采样仪测定后20 min的平均粉尘质量浓度，采用同样的方法得到两个平面的粉尘质量浓度分布等值线图如图6所示.

从图6可以看出：

1）与只有B点作业相比，3个点同时进行打磨

作业产生的粉尘量大大增加，测定后20 min的平均質量浓度是单尘源的2～3倍，最高质量浓度达45.73 mg/m3，最低质量浓度为14.10 mg/m3，远高于规定值.

2）在z = 0平面，粉尘质量浓度的“聚集点”并没有出现在3个打磨点处，而是位于打磨点间的正前方，呈“双峰”型. 因为在同一Y值处，两个打磨点中间的位置存在耦合效果，粉尘质量浓度要高于打磨点正前方位置的粉尘质量浓度，所以在每个Y值下，沿X方向都存在两个“驼峰”. 且由于打磨产生的粉尘以一定的初速度向前运动，最终“聚集点”出现在点与点之间正前方1～1.5 m位置处.

3）在呼吸带高度z=0.7处，与z=0平面类似，也存在两个“聚集点”，但其距离打磨点的垂直距离较远. 因为打磨时，砂轮以一定角度倾斜，产生的粉尘和火花向前运动时，也以一定角度向上运动，所以“聚集点”的位置比z=0平面更远;相应地，能够扩散到呼吸带高度的粉尘数量与z=0平面相比有所下降，所以测得该平面平均粉尘质量浓度要低于z=0平面.

3   多尘源耦合粉尘扩散模型系数的求解

根据建立的打磨作业多尘源耦合扩散模型和实验测定的粉尘质量浓度，采用极大似然估计法和梯度下降法，对模型中未知参数进行求解，即扩散系数Dx、Dy、Dz 和多尘源耦合系数k0、k1、k2、k3，从而得出打磨作业多尘源耦合扩散规律的详细表达式.

3.1   扩散系数求解

根据流体扩散和统计理论分析得到打磨点粉尘扩散模型，如式（13）所示，即粒子扩散质量浓度的分布近似符合正态分布，粉尘质量浓度可以用概率来表示，将模型看做均值为打磨点坐标，方差为扩散系数的高斯分布函数. 令σ2

z = 2Dz，将其转化为标准高斯函数，如式（15）所示. 当粒子在空间内做非等速直线运动，且处于斯托克斯区时，最终的沉降速度vt如式（16）所示.

式中：vt为沉降速度，m/s;t为运动时间，s;ρp为粒子密度，kg/m3;ρg为空气密度，kg/m3;dp为粒子粒径，m;CD为粒子运动的阻力系数.

理论上，打磨作业过程中产尘强度M不是恒定的，粉尘的粒径也不同. 为了简化模型，假设打磨的产尘强度M和粒径分布是稳定的，通过打磨前后工件的质量变化和打磨时间，得到M = 6 mg/s. 当室温为20 ℃时，空气的动力粘性系数μg = 1.8 × 10-5 Pa·s，空气压力P = 1 × 105 Pa，空气密度ρg = 1.205 kg/m3. 假设打磨产生的粉尘颗粒为球形颗粒，取其平均粒径计算粉尘的沉降速度，经测定，平均粒径dp为120 μm，密度ρp为7 900 kg/m3，粉尘的初始扩散速度为

1 m/s，得到粉尘颗粒在空气中流动的雷诺数为：

粒子运动的雷诺数Re = 8.03，根据气溶胶力学可知，粒子运动的阻力系数处于过渡区，不需要进行肯宁汉修正[17]，即CD为：

粉尘粒子在空间内做非等速运动时，由于颗粒粒径较大，处于过渡区，斯托克斯定律不再适用，需要通过无因次数（Re/CD）1/3求取最终的沉降速度，如式（19）.

所以当打磨产生的粉尘粒子在空间内做非等速运动时，最终的沉降速度vt为0.67 m/s，且打磨点B的坐标为（0，0，0），距地面高度H为0.8 m.

采用Matlab编程，对打磨作业粉尘扩散的规律进行多元高斯函数非线性拟合，将单点打磨测定的实验数据迭代求解，设定收敛条件为10-10. 进行55 000步迭代计算后，达到收敛条件，得到σx、σy、σz分别为0.77、0.94、20.45，进而得到Dx、Dy、Dz分别为0.30 m2/s、0.44 m2/s、209.10 m2/s.

3.2   耦合系数求解

对于多尘源粉尘扩散耦合模型，假设粉尘源之间的关系为线性回归耦合，即多尘源状态下，任意一点P的粉尘质量浓度值与各个打磨点单独作业在P产生的粉尘质量浓度值满足线性耦合关系，如式（14）.

采用梯度下降法，对耦合系数k0，k1，k2，k3进行求解. 通过建立损失函数，计算实测的训练集与构建的预测函数之间的误差，寻求最佳的预测函数拟合值. 本文采用均方根代价函数的方法，确定多尘源粉尘耦合扩散模型的损失函数L（k0，k1，k2，k3），其中n为训练集的数据点个数，c（x，y，z）为预测函数，c测（x，y，z）为实测点数据.

对于均方根损失函数，其最小值即为二次函数的最低点，对应的梯度L/k为0，对L（k0，k1，k2，k3）最小值的求解，可转化为对其梯度L/k的求解.

对于上述公式，很难直接求出其梯度等于0的点，采用迭代法进行计算，使L/k逐步趋于0，从而得到在误差范围内对应的最优解.

将多点打磨实验测定的数据作为训练集，代入损失函数中，用Matlab进行迭代计算，计算的基础条件与求解扩散系数相同，设迭代步长为0.05，收敛条件为10-3. 进行1 000步迭代计算后，达到收敛条件，得出的耦合系数值分别为，k0 = 0.026，k1 = 0.27，k2 = -0.39，k3 = -0.20.

4   打磨作业粉尘扩散理论模型的验证

为比较迭代后所得模型的可靠性，对模型计算的理论值与对照实验组数据的偏差进行计算分析. 在B点单独作业的情况下，取z=0 m和z=0.7 m两个平面的对照组实验粉尘质量浓度值，计算与理论值的误差，并取其绝对值进行分析. 如图7所示，前18个点为z = 0 m平面的数据及其误差，后18个点为z=0.7 m平面的数据及其误差，对其误差进行分析可知，所有测点数据误差的平均值为18.77%，其中不超过20%的测点占66.7%，不超过40%的占91.67%.

同理，当A、B、C 3个點同时进行打磨作业时，测点实测值、理论值，以及其误差如图8所示，对其误差进行分析得：所有测点数据误差的平均值为14.67%，不超过20%的数据占77.78%，不超过40%的占97.22%.

通过以上分析，可以看出：

1）推导和迭代得到的打磨粉尘扩散模型理论值与实验测定结果相比，虽然存在一定的误差，但没有误差超过50%的点，绝大部分在20%以下，单尘源和多尘源的平均误差分别为18.77%和14.67%.

2）虽然得到的模型存在偏差，但在可接受范围内. 存在误差的原因一部分是建模时，对模型做了简化，如假设空间内无扰动气流、将粉尘看作大小相同的球形颗粒等;另一部分是，实验过程中难免存在人为误操作和仪器误差.

3）通过对误差的比较分析，说明建立的单尘源粉尘扩散模型和多尘源耦合扩散模型，可以用于研究打磨作业场所的粉尘扩散规律，对现场防尘工作有一定的指导意义. 但由于打磨实验和现场测定的粉尘运动处于过渡区，该计算模型仅适用Re为1～500的情况.

5   结   论

1）打磨作业粉尘扩散规律在空间内满足多元高斯分布，结合重力场的粉尘沉降效果，建立了理想状态的单尘源粉尘扩散模型，采用线性回归方法，基于单尘源扩散规律得到了多尘源耦合扩散模型.

2）实验测定的不同高度粉尘质量浓度分布规律的结果表明，单点打磨时，距离源点越近，高度越低，粉尘质量浓度越高，且向前呈放射状分布;当3个点同时进行打磨时，产生的粉尘质量浓度是单尘源的2～3倍，且打磨点附近粉尘平均质量浓度也远高于规定值，必须采取防护措施.

3）打磨产生的粒子在空气中运动，其阻力位于过渡区，通过无因次数（Re /CD）1/3，求得其最终沉降速度为0.67 m/s;再结合单点打磨实验测定的3组不同高度的粉尘质量浓度数据，采用Matlab拟合求解，得到Dx、Dy、Dz分别为0.30 m2/s、0.44 m2/s、209.10 m2/s;进一步采用梯度下降法，求解得到尘源之间的线性耦合关系，耦合系数k0 = 0.026，k1 = 0.27，k2 = -0.39，k3 = -0.20.

4）将得到的单尘源和多尘源模型的理论值与实测值进行对比验证，理论值与实测值虽然存在一定偏差，但其分布规律相似，说明建立的粉尘扩散模型具有一定可靠性，可用于研究打磨作业场所的粉尘扩散规律，并指导现场防尘工作.

参考文献

[1]    袁竹林. 气固两相流动与数值模拟[M]. 南京：东南大学出版社，2013：196.

YUAN Z L. Gas-solid two-phase flow and numerical simulation [M]. Nanjing：Southeast University Press，2013：196. （In Chinese）

[2]    ZHOU G，FENG B，YIN W J，et al. Numerical simulations on airflow-dust diffusion rules with the use of coal cutter dust removal fans and related engineering applications in a fully-mechanized coal mining face[J]. Powder Technology，2018，339：354—367.

[3]    LIU Q，NIE W，HUA Y，et al. Research on tunnel ventilation systems：dust diffusion and pollution behaviour by air curtains based on CFD technology and field measurement [J]. Building and Environment，2019，147：444—460.

[4]    CAI P，NIE W，HUA Y，et al. Diffusion and pollution of multi-source dusts in a fully mechanized coal face [J]. Process Safety and Environmental Protection，2018，118：93—105.

[5]    ZHAO B，WU J. Particle deposition in indoor environments：analysis of influencing factors [J]. Journal of Hazardous Materials，2007，147：439—448.

[6]    ZHAO B，YANG C，YANG X，et al. Particle dispersion and deposition in ventilated rooms：testing and evaluation of different eulerian and lagrangian models [J]. Building and Environment，2008，43：388—397.

[7]    ZHAO Y M，KINGSLY AMBROSE R P. Modeling dust dispersion and suspension pattern under turbulence [J]. Journal of Loss Prevention in the Process Industries，2019，62：103934.

[8]    李明. 计算机在粉尘扩散及危害预测与环境经济分析中的应用研究[D]. 长沙：中南大学资源与安全工程学院，2005：11—16.

LI M. Application of computer in dust diffusion and hazard prediction and environmental economic analysis[D]. Changsha：School of Resources and Safety Engineering，Central South University，2005：11—16. （In Chinese）

[9]    李明，吴超. 粉尘点污染扩散模型的可视化研究[J]. 环境科学与技术，2006（11）：12—14，115—116.

LI M，WU C.Visualization of dust point pollution diffusion model [J]. Environmental Science and Technology，2006（11）：12—14，115—116. （In Chinese）

[10]  蒋仲安，陈雅，王佩. 双尘源耦合下呼吸性粉尘扩散的紊流系数求解[J]. 哈尔滨工业大学学报，2017，49（8）：129—134.

JIANG Z A，CHEN Y，WANG P.Solution of turbulence coefficient of respiratory dust diffusion under double dust source coupling [J]. Journal of Harbin Institute of Technology，2017，49（8）：129—134. （In Chinese）

[11]  王洪胜，谭聪，蒋仲安，等. 综放面多尘源粉尘分布规律数值模拟及实测[J]. 哈尔滨工业大学学报，2015，47（8）：106—112.

WANG H S，TAN C，JIANG Z A，et al. Numerical Simulation and measurement of dust distribution law of dust source in fully mechanized caving face [J]. Journal of Harbin Institute of Technology，2015，47（8）：106—112. （In Chinese）

[12]  蔣仲安，高康宁，陈记合，等. 移动式打磨作业粉尘分布规律及其影响因素[J]. 中南大学学报（自然科学版），2019，50（5）：1028—1034.

JIANG Z A，GAO K N，CHEN J H，et al. Distribution of dust in mobile grinding operation and its influencing factors [J]. Journal of Central South University（Science and Technology），2019，50（5）：1028—1034. （In Chinese）

[13]  高康宁，蒋仲安，陈记合，等. 冲压车间打磨区粉尘分布规律数值模拟与实测[J]. 中国安全生产科学技术，2018，14（4）：181—186.

GAO K N，JIANG Z A，CHEN J H，et al. Numerical Simulation and measurement of dust distribution law in the grinding area of stamping workshop [J]. China Safety Science and Technology，2018，14（4）：181—186. （In Chinese）

[14]  黄武，汪圣华，张金锋，等. 手持砂轮打磨金属粉尘微观特征研究[J]. 安全與环境学报，2019，19（2）：431—435.

HUANG W，WANG S H ZHANG J F，et al. Study on microscopic characteristics of metal dust grinding by hand-held grinding wheel [J]. Journal of Safety and Environment，2019，19（2）：431—435. （In Chinese）

[15]  蒋仲安，兰桂，彭亚. 焊接车间多尘源粉尘分布数学模型和验证[J]. 焊接学报，2019，40（4）：67—72，163—164.

JIANG Z A，LAN G，PENG Y . Mathematical model and verification of multi-dust source dust distribution in welding workshop [J]. Journal of Welding，2019，40（4）：67—72，163—164. （In Chinese）

[16]  林浩宇，蒋仲安，杨斌，等. 组合式通风打磨台风量对粉尘控制效果的影响[J].中国安全生产科学技术，2018，14（11）：160—165.

LIN H Y，JIANG Z A，YANG B，et al. Influence of combined ventilation and typhoon on dust control effect [J]. China Safety Science and Technology，2018，14（11）：160—165. （In Chinese）

[17]  蒋仲安. 气溶胶力学及应用[M]. 北京：冶金工业出版社，2018：50.

JIANG Z A. Aerosol mechanics and application [M]. Beijing：Metallurgical Industry Press，2018：50. （In Chinese）