磁电弹结构多场耦合分析的稳定Node-based光滑径向基点插值法

任书慧 孟广伟 王吉贤 周立明?

摘   要：为提高磁电弹结构分析的精度，提出稳定Node-based光滑径向基点插值法（SNS-RPIM）. 基于传统Node-based光滑径向基点插值法（NS-RPIM），引入与场变量梯度方差有关的稳定项，消除不确定参数，推导了多场耦合问题的SNS-RPIM方程，求解了磁电弹结构静力响应问题，并与有限元法计算结果进行比较. 数值算例结果表明，SNS-RPIM能够得到更加接近真实解的结果，有效解决了有限元系统刚度偏硬的问题;在精度与收敛性方面，SNS-RPIM比有限元法表现得更加出色，从而为磁电弹材料的进一步应用提供了有效的分析方法.

关键词：稳定光滑径向基点插值法;磁电弹材料;复合材料;梯度光滑技术;数值方法

中图分类号：TB115                             文献标志码：A

Stabilized Node-based Smoothed Radial Point Interpolation Method

for Multi-field Coupling Analysis of Magneto-electro-elastic Structures

REN Shuhui，MENG Guangwei，WANG Jixian，ZHOU Liming?

（School of Mechanical and Aerospace Engineering，Jilin University，Changchun 130025，China）

Abstract： In order to improve the accuracy in analyzing magneto-electro-elastic （MEE） structures， a stabilized node-based smoothed radial point interpolation method （SNS-RPIM） was proposed. Based on the traditional node-based smoothed radial point interpolation method， the stable item related to the gradient variance of the field variables was introduced to eliminate the uncertain parameter. The SNS-RPIM equations for multi-field coupling problems were derived， and the static responses of MEE structures were also solved. The results of SNS-RPIM were compared with those of finite element method. Numerical examples showed that SNS-RPIM can provide the result closer to the real solution and effectively solve the problem of 'overly-stiff' of finite element method. SNS-RPIM is better than FEM in terms of accuracy and convergence， which provides an effective analysis method for further application of MEE materials.

Key words： stabilized smoothed radial point interpolation method; magneto-electro-elastic（MEE） material;composite material;gradient smoothing technique;numerical methods

磁電弹材料是一种由压电相（BaTiO3）与压磁相（CoFe2O4）复合而成的智能材料，能够将机械能、电能与磁能相互转化[1-2]. 磁电弹材料因其具有力电、力磁、磁电效应而被广泛应用于智能结构中，引起了国内外学者的广泛关注[3-4]. Jiang等[5]推导了在均布载荷作用下磁电弹悬臂梁响应的解析解，为未来磁电弹结构的设计与分析奠定了基础. Wang等[6]求解了三维磁电弹圆柱板的自由振动问题，得出了频率方程. Ebrahimi等[7-8]利用Hamilton原理推导了磁电弹纳米板的非局部控制方程，研究了纳米板的屈曲行为.

由于传统有限元法（FEM）在求解中存在“过刚”、体积自锁等问题，导致结果不准确. 近年来，Liu等[9]提出了广义梯度光滑技术，并基于该方法构造出了一系列光滑有限元法（S-FEM）[10]和光滑径向基点插值法（S-RPIM）[11]. 何智成等[12-13]和陈泽聪等[14]将光滑有限元应用到声学模拟中. 周立明等[15-16]将光滑有限元扩展到了求解裂纹问题和多场耦合问题中，验证了光滑方法的准确性. 在S-RPIM中，Node-based光滑径向基点插值法（NS-RPIM）能够消除FEM中“过刚”的问题，为所求解问题提供能量范数的上界解[9].该方法使用径向基函数对场函数进行近似，其形函数具有Kronecker Delta函数属性，边界条件可以如FEM一样直接施加. 基于伽辽金弱形式与节点积分技术，推导出系统方程. 基于这些优点，NS-RPIM在求解静力学以及多场耦合问题中得到了广泛的应用. Li等[17]采用NS-RPIM分析了二维、三维固体力学问题，验证了此算法的准确性与优越性. Zhou等[18]将NS-RPIM引入多场耦合问题的研究中，结果表明，NS-RPIM对于求解磁电弹结构的响应问题是有效且可靠的.

尽管NS-RPIM在求解许多问题时表现良好，但研究表明[11，19]，由于NS-RPIM的模型过于柔软，会令其在求解动态问题时产生伪非零能量模式，导致算法存在时间不稳定性. 为增强系统刚度，解决时间不稳定性，Wang等[20]提出了一种稳定算法，解决了Node-based光滑有限元方法中的缺陷并且减少了求解声学问题中的色散误差. Feng等[21]提出了一种稳定的节点积分方法，分析了电磁问题. Yang等[22]解决了Node-based光滑有限元方法中的时间不稳定性，更准确的求解了金属成型问题.

本文提出了稳定NS-RPIM （SNS-RPIM），基于傳统NS-RPIM方法，引入与场变量梯度方差相关的稳定项，消除了不确定参数，推导了求解多场耦合问题的SNS-RPIM方程，分析了磁电弹结构在静力作用下的响应，并将所得结果与有限元法计算结果进行了对比.

1   基本方程

磁电弹材料平衡方程如下：

σij，j = 0，（i，j = 1，2，3）      （1）

Dl，l = 0，（l = 1，2，3）      （2）

Bl，l = 0，（l = 1，2，3）      （3）

式中：σij、Dl、Bl分别为应力分量、电位移分量、磁感应强度分量.

磁电弹材料的几何方程如下：

Sij = （ui，j + uj，i），（i，j = 1，2，3）      （4）

Ek = -Φ，k，（k = 1，2，3）      （5）

Hk = -Ψ，k，（k = 1，2，3）      （6）

式中：Sij为应变分量;Ek为电场强度分量;Hk为磁场强度分量;Φ与Ψ为电势与磁势.

磁电弹材料的本构方程如下：

σi = Cij Sj - eki Ek - qki Hk        （7）

Dl = elj Sj + εlk Ek + mlk Hk        （8）

Bl = qlj Sj + mlk Ek + μlk Hk        （9）

式中：Cij、eki、qki 分别为弹性常数、压电系数与压磁系数;εlk、mlk、 μlk 分别为介电常数、磁电耦合系数与磁导率. i，j = 1，2，… ，6; l = 1，2，3; k = 1，2，3.

边界条件为：

ui = [u][～]i，在Γd上       （10）

σij nj = [β][～]i，在Γs上，Γ = Γd ∪Γs    （11）

Φ = [Φ][～]，在Γe上       （12）

Dl nl = [Q][～]i，在Γt上，Γ = Γe ∪Γt    （13）

Ψ = [Ψ][～]，在Γm上       （14）

Bl nl = [R][～]，在Γi上，Γ = Γm ∪Γi    （15）

式中：Γd与Γs分别为位移边界与力边界;Γe与Γt分别为电势边界与电位移边界;Γm与Γi分别为磁势边界与磁通量边界;[u][～]为Γd上给定的位移;[β][～]为Γe上给定的面力;[Φ][～]为Γe上给定的电势;[Q][～]为Γt上给定的电位移;[Ψ][～]为Γm上给定的磁势;[R][～]为Γi上给定的磁通量.

2   稳定Node-based光滑径向基点插值法

2.1   Cell-based T2L方案

Cell-based T2L方案[9]为计算xQ的形函数值选择合适的局部支持节点. 该方案选择xQ周围的两层节点作为局部支持节点. 第一层节点为xQ所在三角形单元的顶点;第二层节点为与第一层节点直接连接的那些节点，如图1所示.

2.2   Node-based光滑径向基点插值法

二维问题域Ω被离散为ne个三角形单元，包含nn个节点. 通过将节点xi = [xi，zi]T周围三角形的边中点与质心依次相连，构造以xi为中心的光滑域Ωi，如图2所示.

问题域内任一点xi处的近似位移u、近似电势Φ与近似磁势Ψ可表示为：

式中：Nu（xi）、NΦ（xi）与NΨ（xi）分别为NS-RPIM的位移形函数、电势形函数与磁势形函数;ns为局部支持节点的数量;u、Φ和Ψ分别表示位移向量、电势向量和磁势向量.

通过引入梯度光滑技术，根据式（16）～（18），节点xi处的光滑应变S、光滑电场强度E与光滑磁场强度H分别为：

式中：Bu（xi）、BΦ（xi）与BΨ（xi）分别为节点光滑应变矩阵、节点光滑电场强度矩阵和节点光滑磁场强度矩阵，其表达式为：

式中：nG为高斯点的数量;nseg为光滑域边界的数量; n t

l，p为光滑域第p段边界中单位法向量矩阵的分量; N t

l，p，q为第p段边界上第q个高斯点处的形函数值; WG

q为第q个高斯点处的权值;Ai为光滑域的面积.

二维磁电弹的NS-RPIM静力学方程可表示为：

式中：等效力向量Feq、等效刚度矩阵Keq以及电势Φ和磁势Ψ的求解公式见参考文献[18].

2.3   稳定Node-based光滑径向基点插值法

为了在提高NS-RPIM计算精度的同时消除时间不稳定性，在该算法中引入与场变量梯度方差相关的稳定项来提高模型的刚度，令其更接近真实情况.

以二維问题为例，如图3所示，光滑域Ωi被近似为具有相同面积的圆，将近似域进一步划分为4个子光滑域. 局部坐标系与光滑域的交点Gk

i（k = 1，2，3，4; i = 1，2，3，…，nn）作为补充积分点，nn为结构包含节点数. 积分点与节点xi之间的距离lc相等，大小为近似域的半径. lc的计算公式为：

假设场变量的梯度在光滑域Ωi中连续且一阶可导，其在4个积分点处的泰勒展开式分别为：

3   数值算例

3.1   算例1

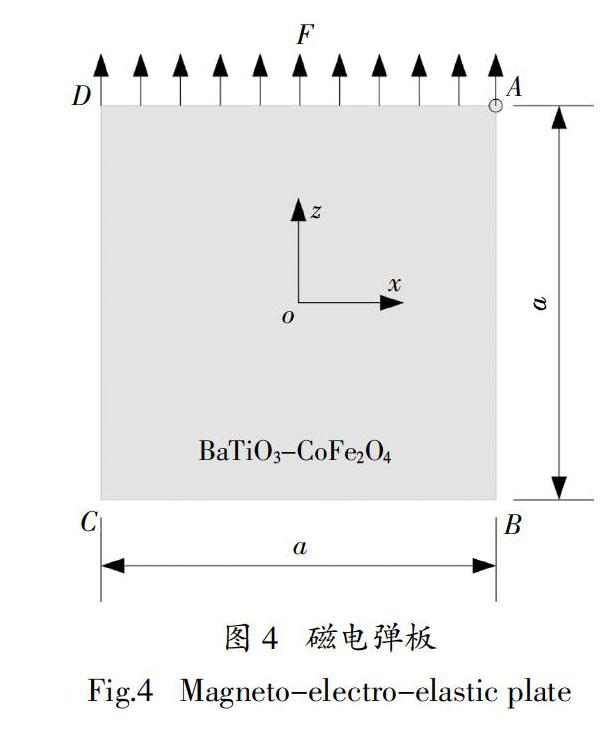
磁电弹材料（BaTiO3-CoFe2O4）板在边AD受100 N/m2的均布载荷作用，为平面应变问题，如图4所示，边长a = 2.0 m. 表1给出了磁电弹板的材料参数，质量密度为5 730 kg/m3，边界条件为：ux = 0（边CD），uz = Ф = Ψ = 0（边BC），每个边界的表面电荷与表面磁感应强度均为零.

采用不同节点数量（121、441和1 681个）求解磁电弹板的广义位移（位移ux、uz，电势Φ，磁势Ψ），验证SNS-RPIM的正确性以及收敛性. 表2给出了文献[23]中A点处位移、电势与磁势的解析解，以及SNS-RPIM在不同节点数量下的计算结果. 可见，SNS-RPIM的结果与解析解误差很小，随着节点数量的增加，误差减小，验证了SNS-RPIM求解磁电弹结构多场耦合问题的正确性、有效性.

3.2   算例2

磁电弹材料悬臂梁如图5所示，长度L=0.030 m，宽度h=0.002 m，在B点承受200 N的静力，为平面应力问题. 悬臂梁在固定端处满足ux=uz=Φ=Ψ =0. 悬臂梁材料属性见表1，质量密度为5 730 kg/m3.

在证明了SNS-RPIM正确性的基础上，对磁电弹悬臂梁在静力作用下的响应进行研究. 图6给出了边AB处的广义位移，SNS-RPIM与FEM采用三角形单元，节点数量为305个. 其中，参考解为FEM采用180×12个四边形单元的结果. 图7给出了静力作用下悬臂梁的云图. 由结果可知，在所用节点数量相同的情况下，SNS-RPIM的计算结果比FEM的结果更加接近参考解. 算例结果验证了SNS-RPIM的高精度、正确性和有效性.

在节点数为305  、637和1 089个时，对比了SNS-RPIM与FEM的能量误差[24]，如图8所示. 可知在节点数相同的情况下，SNS-RPIM的能量误差远远低于FEM，并且随着所用节点数的增加，能量误差逐渐降低. 从而进一步验证了SNS-RPIM的精确性，高收敛性与有效性.

4   结   论

本文基于场变量梯度方差构造了稳定项，并将其引入了传统Node-based光滑径向基点插值法，提出了稳定Node-based光滑径向基点插值法. 随后求解了磁电弹结构在静力作用下的响应，得出以下结论：

1）将SNS-RPIM的结果与解析解进行对比，

二者吻合良好，说明了本方法的正确性及有效性.

2）计算了SNS-RPIM与FEM在不同节点数量

下的能量误差，结果显示SNS-RPIM具有良好的收敛性与准确性.

3）SNS-RPIM利用较少的节点能够达到更高的精度，消除了FEM模型刚度过硬的问题.

4）通过考虑SNS-RPIM与FEM对不同模型的

求解结果，表明SNS-RPIM在求解磁电弹结构多场耦合问题时的可靠性和适用性.

参考文献

[1]    BOOMGAARD J V D，VAN RUN A M J，SUCHTELEN J V. Magnetoelectricity in piezoelectric-magnetostrictive composites [J]. Ferroelectrics ，1976，10（1）： 295—298.

[2]    LU X Y，LI H，WANG B. Theoretical analysis of electric，magnetic and magnetoelectric properties of nano-structured multiferroic composites [J]. Journal of the Mechanics and Physics of Solids，2011，59（10）：1966—1977.

[3]    FETISOV L Y，SEROV V N，CHASHIN D V，et al. A magnetoelectric sensor of threshold DC magnetic fields [J]. Journal of Applied Physics，2017，121（15）：154503.

[4]    李帛书，钟轶峰，罗丹，等. 涂层-纤维增强磁电弹性材料的变分渐近细观力学模型 [J]. 复合材料学报，2018，35（10）： 2823—2831.

LI B S，ZHONG Y F，LUO D，et al. Variational asymptotic micromechanics model of coating-fiber reinforced magneto-electro-elastic materials [J].Acta Materiae Compositae Sinica，2018，35（10）： 2823—2831. （In Chinese）

[5]    JIANG A M，DING H J. Analytical solutions to magneto-electro-elastic beams [J]. Structural Engineering and Mechanics，2004，18（2）：195—209.

[6]    WANG Y，XU R Q，DING H J，et al. Three-dimensional exact solutions for free vibrations of simply supported magneto-electro-elastic cylindrical panels[J]. International Journal of Engineering Science，2010，48（12）：1778—1796.

[7]    EBRAHIMI F，BARATI M R. An exact solution for buckling analysis of embedded piezoelectro-magnetically actuated nanoscale beams [J]. Advances in Nano Research，2016，4（2）：65—84.

[8]    EBRAHIMI F，BARATI M R. Static stability analysis of smart magneto-electro-elastic heterogeneous nanoplates embedded in an elastic medium based on a four-variable refined plate theory [J]. Smart Materials and Structures，2016，25（10）：105014.

[9]    LIU G R，ZHANG G Y. Smoothed point interpolation methods G space theory and weakened weak forms[M]. Singapore： World Scientific，2013： 403—578.

[10]  崔向陽，李光耀. 基于边光滑有限元法的剪切变形板几何非线性分析 [J]. 计算机辅助工程，2011，20（1）： 155—162.

CUI X Y，LI G Y.Geometric nonlinear analysis on shear deformation plates using edge-based smoothed finite element method [J].Computer Aided Engineering，2011，20（1）： 155—162. （In Chinese）

[11]  LIU G R，LI Y，DAI K Y，et al. A linearly con-forming radial point interpolation method for solid mechanics problems[J]. International Journal of Computational Methods，2006，3（4）：401—428.

[12]  何智成，李光耀，成艾国，等. 光滑有限元的声学研究：时域和频域分析 [J]. 振动与冲击，2012，31（16）：122—127.

HE Z C，LI G Y，CHENG A G，et al.Acoustic analysis using edge-based smoothed finite element method： time and frequency domain analysis[J]. Journal of Vibration and Shock，2012，31（16）： 122—127. （In Chinese）

[13]  何智成，李光耀，成艾国，等. 基于边光滑有限元的声固耦合研究 [J]. 机械工程学报，2014，50（4）： 113—119.

HE Z C，LI G Y，CHENG A G，et al.Coupled edge-based smoothing finite element method for structural acoustic problems [J]. Journal of Mechanical Engineering，2014，50（4）： 113—119. （In Chinese）

[14]  陈泽聪，陈毓珍，何智成，等. 应用混合单元基光滑点插值法的声固耦合分析 [J]. 振动与冲击，2019，38（8）： 238—245.

CHEN Z C，CHEN Y Z，HE Z C，et al.A hybrid cell-based smoothing point interpolation method for solving structural-acoustic problems [J]. Journal of Vibration and Shock，2019，38（8）： 238—245. （In Chinese）

[15]  周立明，孟廣伟，李锋. 界面裂纹的Cell-Based光滑有限元法研究 [J]. 湖南大学学报（自然科学版），2016，43（6）： 34—39.

ZHOU L M，MENG G W，LI F.Research on cell-based smoothed finite element method of interface cracks [J].Journal of Hunan University （Natural Sciences），2016，43（6）： 34—39. （In Chinese）

[16]  周立明，蔡斌，孟广伟，等. 含裂纹压电材料的Cell-Based光滑扩展有限元法 [J]. 复合材料学报，2016，33（4）： 929—938.

ZHOU L M，CAI B，MENG G W，et al.Cell-based smoothed extended finite element method for piezoelectric materials with cracks [J].Acta Materiae Compositae Sinica，2016，33（4）： 929—938. （In Chinese）

[17]  LI Y，LIU G R，YUE J H. A novel node-based smoothed radial point interpolation method for 2D and 3D solid mechanics problems [J]. Computers & Structures，2018，196：157—172.

[18]  ZHOU L M，REN S H，MENG G W，et al. A multi-physics node-based smoothed radial point interpolation method for transient responses of magneto-electro-elastic structures [J]. Engineering Analysis with Boundary Elements，2019，101：371—384.

[19]  FENG H，CUI X Y，LI G Y，et al. A temporal stable node-based smoothed finite element method for three-dimensional elasticity problems [J]. Computational Mechanics，2014，53（5）：859—876.

[20]  WANG G，CUI X Y，FENG H，et al. A stable node-based smoothed finite element method for acoustic problems [J]. Computational Methods in Applied Mechanics and Engineering，2015，297：348—370.

[21]  FENG H，CUI X Y，LI G Y. A stable nodal integration method for static and quasi-static electromagnetic field computation [J]. Journal of Computational Physics，2017，336：580：594.

[22]  YANG H，CUI X Y，LI S，et al. A stable node-based smoothed finite element method for metal forming analysis [J]. Computational Mechanics，2019，63（6）：1147—1164.

[23]  ZHU X Y，HUANG Z Y，JIANG A M，et al. Fast multipole boundary element analysis for 2D problems of magneto-electro-elastic media [J]. Engineering Analysis with Boundary Elements，2010，34： 927—933.

[24]  ZHOU L M，REN S H，LIU C Y，et al. A valid inhomogeneous cell-based smoothed finite element model for the transient characteristics of functionally graded magneto-electro-elastic structures [J]. Composite Structures，2019，208：298—313.