从习题走向问题

金妤茜

习题是巩固知识、培养学生数学思维的重要载体。若是将一道习题变为一个好的问题，则可引导学生进一步探索、思考新问题，从而激发学生内在的想象力，促进学生深度思考。本文以圆柱、圆锥的习题为例，变习题为问题，引导学生从平面图形到立体图形，感受平面图形与立体图形之间的联系，并在操作想象中培养学生的空间观念，在问题解决中发展学生的数学思维。笔者的思考源自苏教版数学教材六年级下册圆柱的体积和圆锥的体积两道练习题（如下图）。

前一题的编排意图是：一是通过演示、操作和想象，使学生初步认识到圆柱可以看作一个长方形绕着它的一条边旋转一周后得到的立体图形;二是让学生看图说说题中的两个圆柱的底面半径和高各是多少;三是估计哪个圆柱体积大时，可以直接比较4×4×5与5×5×4的大小。后一题的编排意图是：让学生结合直观图说说旋转成的圆锥的底面半径和高各是多少，再分别计算两个圆锥的体积，还可以引导学生比较发现，绕短直角边旋转一周后所形成的圆锥体积比较大。这两题的题型类似，目标相近，主要是帮助学生认识圆柱和圆锥可由长方形或直角三角形旋转而来，感受其旋转体的特征，进一步积累图形与几何的学习经验，培养初步的比较、分析、综合、抽象、概括以及简单的判断、推理能力，发展数学思考，增强空间观念。教师可将这个知识点安排在不同练习课上作为习题呈现，教学时学生根据图示计算出各自的体积并比较大小后，教师就一带而过了。如此，学生对平面图形与立体图形之间的联系感受明显不够，对旋转体本质的感悟也并不深刻。

联系前后知识，笔者尝试将两道练习题转化成具有一定开放性和综合性的问题解决过程，主要设计了三个环节，并调整至圆柱、圆锥体积教学全部完成后再研究，课堂上给予学生充分的思考时间，让学生在操作、想象中发展空间观念，在问题解决中发展数学思维。

一、夯实基础，沟通知识联系

师：这个单元我们主要认识了圆柱和圆锥，从这两个图形里你能找到或想到哪些平面图形？

（学生小组讨论后汇报交流）

生：直接观察得到平面图形是圆。

生：将圆柱和圆锥切割后的截面是长方形（正方形）、三角形、圆。

生：将圆柱和圆锥侧面展开得到长方形（正方形）、扇形。

（交流中学生适时复习圆柱、圆锥的特征和表面积、体积的计算方法）

【思考】《义务教育数学课程标准（2011年版）》对空间观念有这样一处描述：“空间观念主要是指根据物体特征抽象出几何图形，根据几何图形想象出所描述的实际物体。”本教学环节教师鼓励学生从立体图形中寻找平面图形，此时学生就会用观察、展开、切割等方法，而这些方法除了需要动手操作，更多的是想象，想象是发展学生空间观念的最佳途径。正是这样一个充满想象与挑战的环节，有效地培养了学生的空间观念。整个教学过程学生不仅初步感知了平面图形与立体图形的联系，也在交流中适时复习圆柱、圆锥的特征和表面积、体积的计算方法，为后续的研究夯实基础。

二、建构模型，发展空间观念

（一）操作后想象

师：立体图形中有着很多平面图形的影子，那由一个平面图形可以得到圆柱或圆锥吗？

学生小组合作，借助平面图形操作或直接想象，讨论后汇报交流。

方法1：由平面图形围成。

小组1：（用长方形纸边操作边汇报）用一个长方形围成一个圆柱，而且每个长方形围成圆柱有两种不同的围法（如下图）。

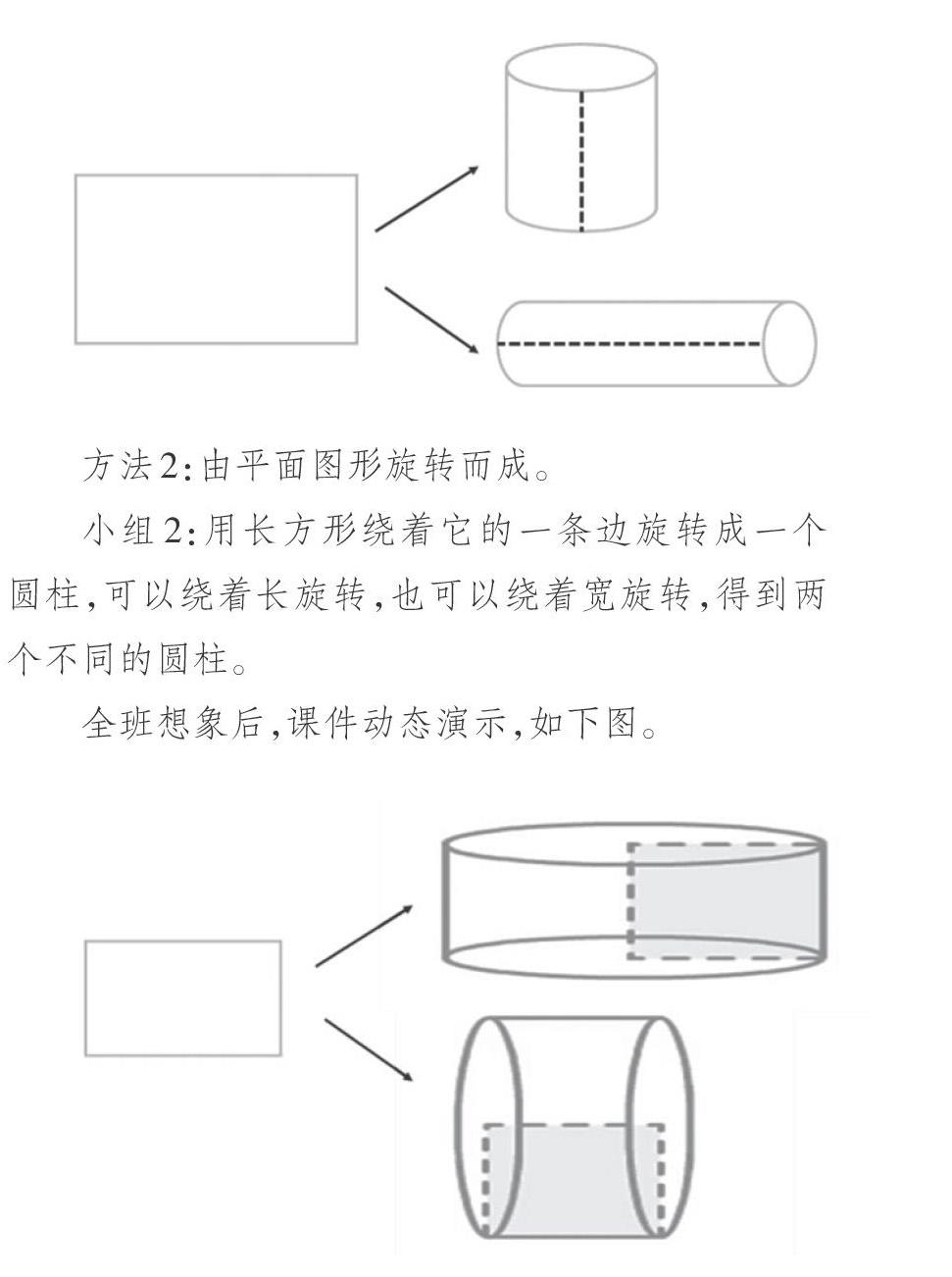
方法2：由平面图形旋转而成。

小组2：用长方形绕着它的一条边旋转成一个圆柱，可以绕着长旋转，也可以绕着宽旋转，得到两个不同的圆柱。

全班想象后，课件动态演示，如下图。

小组3：我们想到的是直角三角形绕着它的一条直角边旋转可以形成一个圆锥，因为直角三角形有两条直角边，所以可以形成两个不同的圆锥。

全班想象后，课件动态演示（图略）。

（二）猜想后验证

师：同学们想到了用平面图形围或者旋转来得到圆柱或圆锥，而同一个图形围或者旋转都有两种情况，对此有什么想法？

生：同一个图形的两种情况下的圆柱或圆锥的体积一样吗？

（学生猜想，产生分歧）

师：你们准备怎么研究？

生：假设数据再计算。

学生分小组进行计算验证并得出结论：（1）长方形以短边为高围成的圆柱体积比较大;（2）长方形绕着宽旋转得到的圆柱体积比较大;（3）直角三角形绕着短直角边旋转得到的圆锥体积比较大。

（三）比较后思考

师：这3个结论有什么共同之处？

生：都是以短边为高时，体积比较大。

师：为什么以短边为高形成的圆柱（圆锥）体积比较大呢？

生：因为圆柱和圆锥的体积计算公式都有πr2h，要想体积大，其中r起了更为重要的作用，短边为高时，长的一边就决定了r的大小，所以这个时候体积就会比较大。

【思考】在图形的变换和运用中，教师引导学生操作和想象，培养学生几何直观能力。教师让学生思考如何从一个平面图形变成一个立体图形，不管是围还是旋转，都先让学生试着想象围或旋转后的图形的样子，再借助课件动态演示，经历由平面图形旋转形成立体图形的探索全过程。然后学生提出问题：“同一个图形围或旋转都有两种情况，这两种情况下的圆柱或圆锥的体积一样吗？”学生先直观猜测，再计算比较并得出结论。教师再次追问：“旋转形成的立体图形中，为什么以短边为高形成的圆柱（圆锥）体积比较大呢？”这一追问进一步激发了学生的思考，学生从计算公式上去解释、去突破。整个教学环节体现了“直观感知—演绎推理—抽象和概括”的思维过程，这个过程中学生的空间想象能力和几何直观能力不断发展，帮助学生顺利地建构几何图形，在建构图形的过程中发展了学生的数学思维。

三、迁移类比，发散数学思维

师：以这个直角三角形的斜边所在的直线为轴旋转一周，会形成怎样的立体图形？这样的立体图形的体积你会计算吗？如果是一个钝角三角形呢？

（1）把你想到的图形在作业纸上画一画。

（2）有困难的学生可以借助老师的学具转一转，再来画。

（3）尝试计算它的体积。

【思考】教师提出“以这个直角三角形的斜边所在的直线为轴旋转一周，会形成怎样的立体图形？”的拓展性问题，将本课的探究推向高潮，学生大胆地运用自己的直觉和想象去体验、去猜測，运用多种方法、通过多种途径去寻求答案。学生基于新问题不断探究，积极主动地思考，不断地发现问题、解决问题，思维能力得到了进一步提升。

综观全课，在整个探究教学过程中，因为习题的整合、变式和拓展，学生从中获得的不仅仅是解答题目本身， 而且通过这道题展开了数学“悟”的过程，是一个主动、深刻的学习过程。好的问题具有生长功能，教师应基于教材，着眼学生发展，试着对教材习题做更深入的研究，将习题转变为问题，让学生有所思、有所为、有所得。

（作者单位：江苏省苏州工业园区星港学校苏安校区）