用Python验证数据结构与算法的关系
浦丕志 赵春芝

在计算机领域,算法实质上就是针对所处理问题的需要,在数据逻辑结构和存储结构的基础上施加的一种运算规则。对问题中的数据的不同组织方式、解决问题的不同的策略将导致不同的算法。在解决实际问题时,要先分析其逻辑关系,建立抽象模型,再选择合理的数据结构来存储数据,通过算法解决其核心问题,实现解决问题的过程。
学生在学习实践中,基本能够合理选择数据结构和算法,但对算法的效率关注不多。在教学中,笔者以“求斐波那契数列的第19项的值”一题为例,让学生体验不同算法之间效率的差异性。
方法1:用递归算法实现求斐波那契数列的第19项的值(如下页图1)。
方法2:用递推算法实现求斐波那契数列的第19项的值(如下页图2)。
两个程序的运行结果相同,但从程序运行时间来看,递推算法优于递归算法。
算法效率
算法效率的高低通常由算法的复杂度来度量。算法复杂度分为时间复杂度和空间复杂度,时间复杂度是指执行算法所需要的计算工作量,而空间复杂度是指执行算法所需要的内存空间。
在学生理解“问题规模”和“时间复杂度表述”方法后,笔者结合例题“求1+2+…+n的和”,帮助学生学习使用Python程序来验证数据结构与算法的关系。
方法1:用等差数列公式实现1+2+…+n的求和(如下页图3)。
这个程序用等差数列公式直接求解,算法中语句执行次数与问题规模n无关,时间复杂度为O(1)。
方法2:用循环结构实现1+2+…+n的求和(如下页图4)。
程序里面用到了循环结构,当问题规模n增大时,循环次数和“s=s+i”的累和过程也线性增大,时间复杂度为O(n)。
从“常量阶”和“线性阶”的对比来看,算法对问题解决的影响很大,也验证了研究算法复杂度的价值和意义。
接下来结合例题“求数列的和”“求2n-1的值”“求递归数列的值”,即时间复杂度分别为O(n2)、O( log2n)、O(2n)的算法,帮助学生理解“平方阶”“对数阶”“指数阶”在程序执行时间随问题规模增长而增长的量级,体验算法的优势,具体代码扫描文末二维码。
时间复杂度
通过学习,学生很容易理解时间复杂度并不是表示程序真正的执行时间,它表示的是程序执行时间随数据规模增长的变化趋势,也是“渐进时间复杂度”,简称“时间复杂度”。在此建议教师给学生提供以下程序资源包,供学生验证使用,程序资源包扫描文末二维码。
此时可以根据程序资源包,测试一下程序运行时间,从而总结出常见的时间复杂度耗费时间的大小关系:O(1)
空間复杂度
教材中通过问题与讨论引导学生通过查阅相关资料,举例说明空间复杂度如何度量。在教学时,建议教师鼓励学生开展合作学习,通过资料查阅和讨论,汇总学习经验,实现对“空间复杂度”的学习。指导学生进行学习的步骤可以安排如下。
1.空间复杂度的概念
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度,记作S(n)。
2.空间复杂度量度
计算机在运行程序时,会包含存储程序空间、输入和输出数据占用的存储空间、程序运行过程中临时产生的存储空间三方面的存储空间。
如果算法占用的临时存储单元不受问题规模大小影响,这种算法就是空间复杂度优秀的算法;有的算法占用的临时存储空间与问题的规模相关,当问题的规模越来越大时(算法没干预)需要的存储空间也越来越大(会溢出),这种算法就需要考虑优化空间复杂度。
3.数据结构所占的空间复杂度
在教学中,建议让学生测试和讨论上面程序,明确字符串类型、一维和多维列表数据类型的空间复杂度。
4.以空间换时间
现在的计算机存储空间都非常大,通常都可以满足程序对大数据存储的需求,因此,在设计算法时,考虑更多的是优化算法的时间复杂度,这就是“空间换时间”。
以“判断素数”为例,可以先用列表存储所有问题规模以内的数据,再使用“筛法”将所有为非素数的列表设置为“False”,完成后再“打表”输出。虽然这种算法在存储素数数组时占用了大量的空间,但当判断某个数是不是素数时,效率非常高,时间复杂度为O(1)。
算法与数据结构是问题求解中相辅相成、不可分割的两个方面。在学习中,可引导学生参与真问题的项目学习,经历建立数据模型、抽象模型、选择数据结构、算法实现、上机调试、问题解决的全过程,从而促进学生形成和提高计算思维能力。
数据结构对算法效率的影响
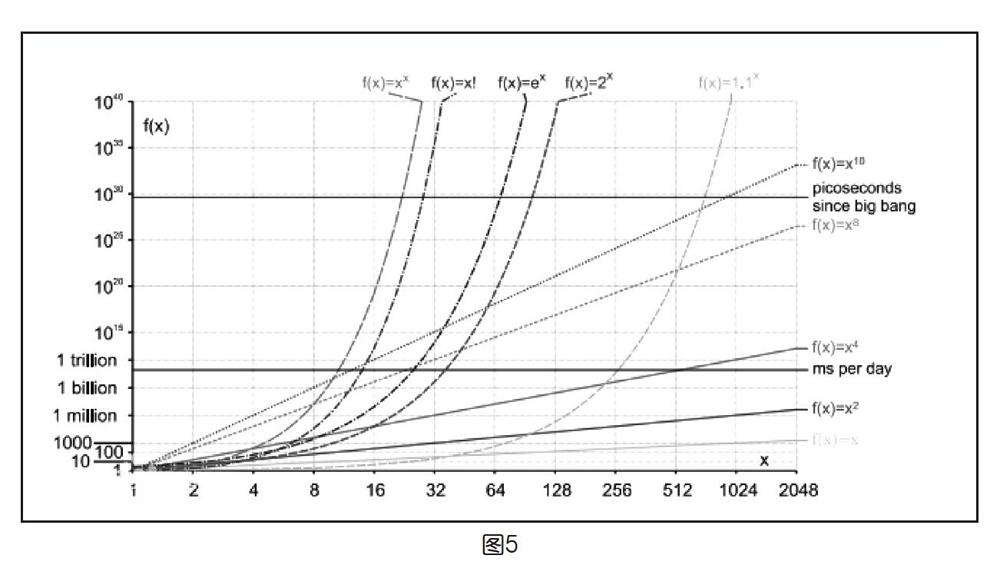
一个算法的复杂度通常是由其输入量决定的,随着输入的增加,不同算法的复杂度增长速度加快,如图5所示。因此,为了降低算法复杂度,在设计算法时,应当同时考虑到输入量的多少。
例如,教材中的显示10000种商品中某个商品的价格问题,从数据结构上说,采用数组比链表更方便;但是如果在10000种商品中添加和删除某一件商品,数据结构采用链表则要优于数组,这也说明了数据结构的不同选择会影响算法的运行效率。
教师在教学过程中,还可以通过下面的程序,帮助学生更好地理解数据结构与算法效率的关系,具体程序代码扫描文末二维码。
当要进行商品信息的添加或删除时,数据结构采用链表优于数组,因为在数组中插入或删除某一个单元会引起大量其他数据的移动,时间复杂度为O(n),在链表中则只需对数据的“域”进行修改,时间复杂度为O(1)。
以上例题(程序)的实践操作,有利于学生对数据结构专业知识的理解。学生在对时间复杂度、空间复杂度的程序验证体验过程中,能够初步形成评估算法效率的能力和针对具体问题优化算法、数据结构的能力,有助于学科核心素养的养成和提高。

