基于背景噪声和特征值下降比的微地震SVD去噪改进方法

王 程， 王维红

( 东北石油大学 地球科学学院，黑龙江 大庆 163318 )

0 引言

随非常规油气勘探的深入，由于布置灵活、成本小、数据采集相对简单，微地震监测技术应用越来越广泛[1]。不同于常规叠前资料噪声压制处理[2]，微地震噪声类型以随机噪声为主，信噪比较低。在微地震去噪方法中，奇异值分解去噪是比较常用的方法[3]，其中确定奇异值有效阶次是关键。

在工程中，一般采用观察奇异值曲线及其突变点或试凑法确定奇异值有效阶次，方法比较繁琐，处理速度较慢，经常出现奇异值选择过多或过少的现象，具有不稳定性[4]。王益艳提出奇异值均值法[5]，将求解奇异值平均值对应点作为有效阶次。赵学智等提出奇异值差分谱法[6]，将相邻奇异值做差得到差分谱，根据差分谱最大值选择有效阶次，在信号信噪比较高的情况下有较好的降噪效果。王树青等利用奇异值相对变化率的最大值确定有效阶次[7]。根据原始信号主频个数的二倍关系，钱征文等确定奇异值分解降噪的有效阶次[8]，在实际工程应用中，受强噪声的影响，很难区分有效信号的主频个数。王建国等提出一种基于奇异值差分谱单边极大值的降噪方法[9]，通过相空间重构Hankel矩阵对原始振动信号进行奇异值分解，确定较大峰值降噪阶数。基于奇异值分解的噪声压制方法，对微地震低信噪比数据等的处理易产生过降噪[10]，或去噪不足现象，存在一定的局限性。

笔者提出一种结合背景噪声最大特征值及特征值下降比、进行有效阶次选择的微地震资料SVD去噪方法。主要利用微地震压裂开始前或压裂结束后背景监测数据，采用奇异值分解方法，根据Weyl鲁棒性原理[11]，分别从背景噪声及原始资料中获取最大特征值及特征值下降比，确定特征值有效阶次，在实际微地震数据处理中去除噪声的同时，最大程度保留弱信号的能量并压制随机噪声，有效避免过降噪等现象。

1 方法原理

1.1 奇异值分解去噪

奇异值分解是对奇异矩阵的特征分解。若一个地震剖面中含有M道地震记录，每道数据有N个采样点，通过本征值提取，那么整个数据可以表示为完整保留原始数据特征的数值矩阵D为

(1)

式中：dm,n为元素，代表地震记录中的信号，m为道号，n为时间采样点序号。矩阵D的奇异值分解可以表示为

D=UΣVT,

(2)

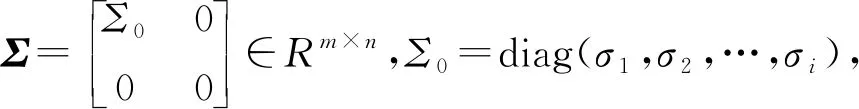
(DTD)νi=λiνi,

(3)

(DDT)ui=λiui。

(4)

由式(3-4)得到矩阵DTD的n个特征值和对应的n个特征向量ν的右奇异矩阵V，以及通过D=UΣVT⟹DV=UΣVTV⟹DV=UΣ⟹Dνi=σiui⟹σi=Dνi/ui，求解每个特征值和奇异值矩阵Σ。

(5)

式中：Hi为σi重构的Hankel矩阵。由于地震有效信号的相关性强，对应的特征值大，矩阵DDT的m个特征值和对应的m个特征向量u的左奇异矩阵U的声信号的相关性差，对应的特征值也小，可先选取矩阵Σ部分较大奇异值的信号，后由式(5)重构Hankel矩阵，还原去除噪声的微地震信号，压制地震信号噪声。

1.2 背景噪声特征值选择

对于自激自收的地面放炮接收的信号，微地震信号的震源在地下，采集到的信号强度较弱，常规处理损害有效信号。在实际处理中，若地震数据的噪声没有完全覆盖，则噪声并不影响初至有效信号的特征值稳定性，根据受噪声扰动的矩阵特征值与未受噪声扰动的特征值之差的上界[12-13]，证明矩阵奇异值分解的稳定性。

根据Weyl定理，当微地震数据D含有随机噪声时，可以表示为

D=B+δ,

(6)

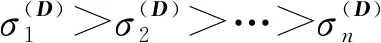
(7)

式中：‖δ‖2为2—范数；δ*为随机噪声矩阵δ的最大奇异值，由谱范数得

(8)

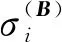
(9)

(10)

β描述矩阵的奇异值递减程度和特征值下降曲线突变情况，每个拐点表示下降变化平稳的特征值，代表奇异值意义改变，即噪声和信号的突变结束，相对于前一特征值对数据贡献的影响较小。

选取压裂结束后背景监测数据，数据为在初至到达时间和停止压裂作业一定时间后采集的信号(主要为随机噪声)，不含初至信息，但背景噪声存在于地震数据采集的整个过程，背景噪声特征值处于一个原始微地震资料中纯信号与噪声的临界，提取时间段数据的噪声特征值中最大的特征值，并结合前后特征值下降比选择特征值，作为改进特征值的依据。

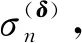
(3)采用式(10)计算前后特征值下降比β，并对β进行赋值，小于阈值的点赋值为0，寻找每一个拐点，确定特征值个数，输出特征值阶次n1。

(5)通过两个约束条件限制n2，作为符合条件的特征值阶次，进行数据重构，完成微地震数据的去噪过程。

2 模型试验

2.1 随机噪声模型试验

采用常规方法中较广泛且具有一定代表性的均值法和差分谱法进行对比。微地震数据的特点是低信噪比，随机噪声较严重，采用一个正演的水平同向轴模型，添加较强的信噪比噪声(sn=2)，形成低信噪比微地震模型测试数据。正演信号震源主频为40 Hz的雷克子波，在一上层为3.6 km/s及下层为4.0 km/s的水平层状速度模型正演的多炮记录的模型(见图1)，对炮集截取50道进行测试。原始正演数据见图1(a)，道数为50道，采样间隔为1 ms，采样时间为2 001 ms；正演模型添加低信噪比的随机噪声后的数据见图1(b)，测试背景噪声为截取添加噪声数据中初至后的数据；改进方法噪声压制后的数据及去噪后残差剖面见图1(c-d)，剖面中无明显信号，采用差分谱法噪声压制后的数据及噪声见图1(e-f)，采用常规均值法噪声压制后的数据及噪声见图1(g-h)；对比文中改进方法(见图1(c))，差分谱法容易损害有效信号，均值法噪声残留较多，改进方法噪声压制效果较理想。

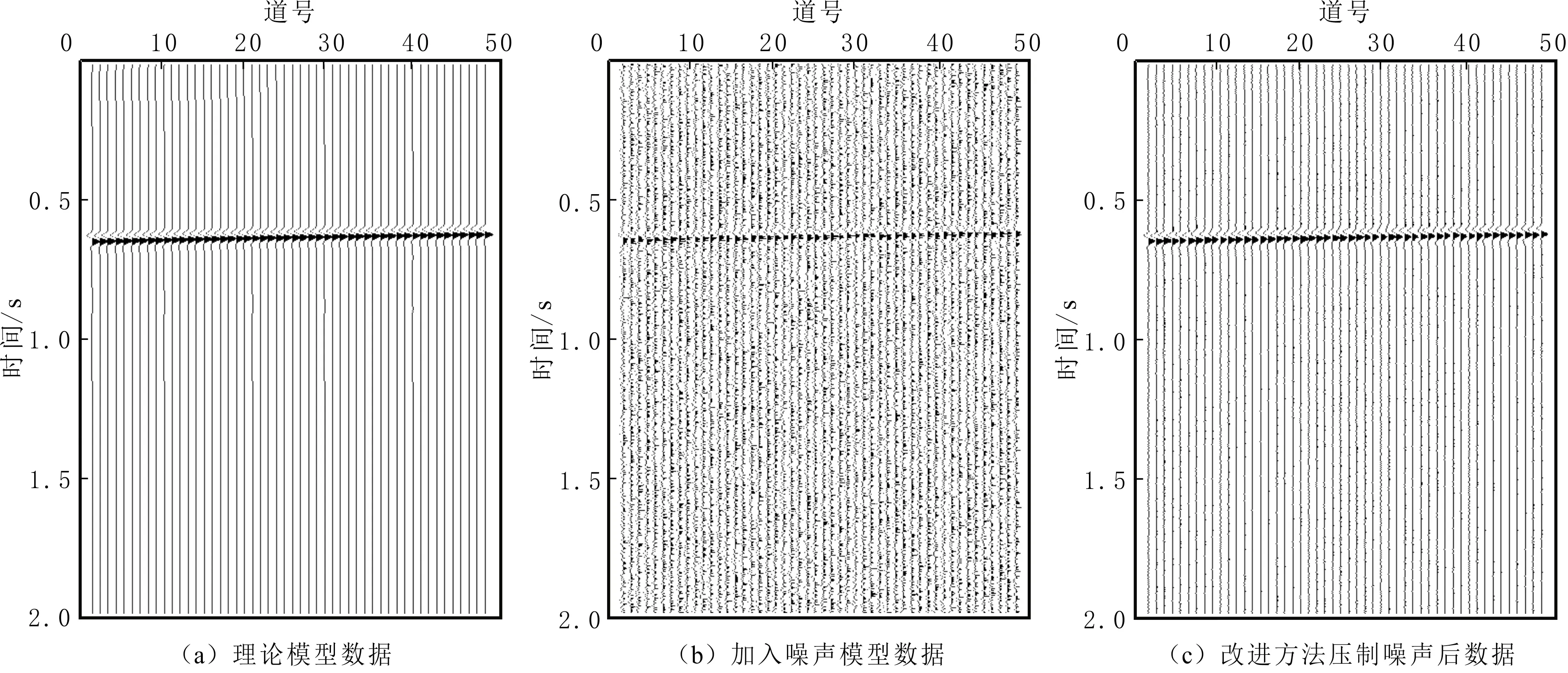
图1 信噪比为2的随机噪声模型测试结果Fig.1 Results of random noise model test with sn=2

2.2 特征值选择

三种方法特征值选择分析见图2。为表明效果，仅显示前49个特征值的变化，改进方法见图2(a)，其中灰色面积为添加随机噪声的正演数据(部分面积被蓝色遮挡)，蓝色面积为背景噪声特征值，红色直线代表背景噪声最大特征值。首先，通过背景噪声最大特征值确定大致范围，在直线与含噪数据的交点附近；然后，在对应交点的附近找到与之对应的下降比曲线上的零点，下降比折线的上升与下降代表特征值下降曲线的突变，每个拐点代表下降变化平稳的特征值，表明奇异值代表的意义改变——噪声和信号突变的结束，缩小范围在下降比折线上找到对应的零点；最后，以24个特征值重构数据。

采用差分谱法处理时，将相邻奇异值做差，依次排列得到差分谱(见图2(b))，根据差分谱最大值选择有效阶次，灰色面积为添加随机噪声的正演数据，蓝色面积为背景噪声特征值。根据差分谱序列，两个相邻的奇异值差别越大，由有用信号和噪声信号的不相关性而导致的峰值越大，在整个差分谱中表现的特征也越明显。根据峰值选取有效阶次，处理数据时，选择特征值过少，易损害有效信号，选择5个特征值进行重构数据时，出现过降噪现象。

采用均值法处理时，灰色面积为添加随机噪声的正演数据，求解奇异值的平均值，将平均值对应的点作为有效阶次(见图2(c))。由于数据特征值较多，若选择全部特征值进行计算，则残留较多噪声，只选择前200个特征值求取平均值，红色虚线为均值法得到的均值线；当选择61个特征值进行数据重构时，对低信噪比数据的处理易导致去噪不足现象。

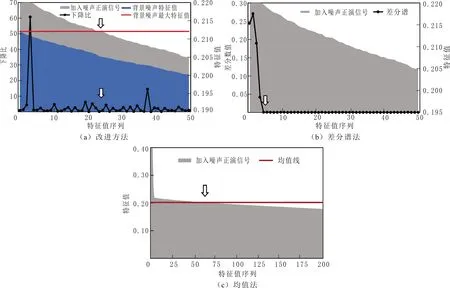
图2 三种方法特征值选择分析Fig.2 Analysis of eigenvalue selection of three methods

2.3 特征值序列

三种方法特征值序列见图3。为表明变化趋势，只选取部分特征值进行显示，其中图3(a-e)分别对应图1(a-e)各阶段数据的特征值序列。由图3(a)可以看到，大多数有效信号数据特征值集中于前半段，少数特征值分布于后半段，对加噪理论数据进行奇异值分解，位于前半段的有效信号的特征值部分受到影响较小，相较于原始理论数据的特征值无明显变化，而噪声部分的奇异值存在范围较大，背景噪声特征值序列见图3(c)。由图3(a、d)可以看到，改进方法选取的特征值未损害有效信号，与差分谱法(见图3(e))和均值法(见图3(f))选取的特征值结果对比，改进方法去噪效果较好。

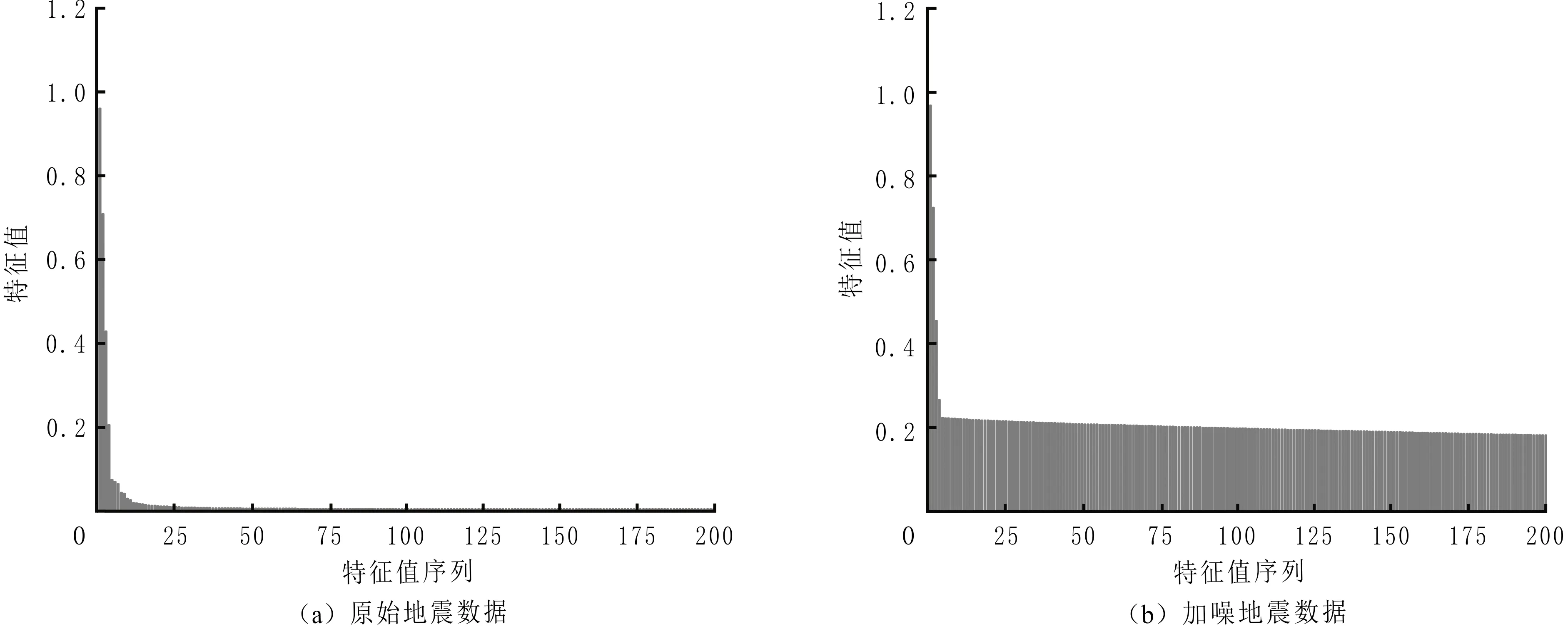
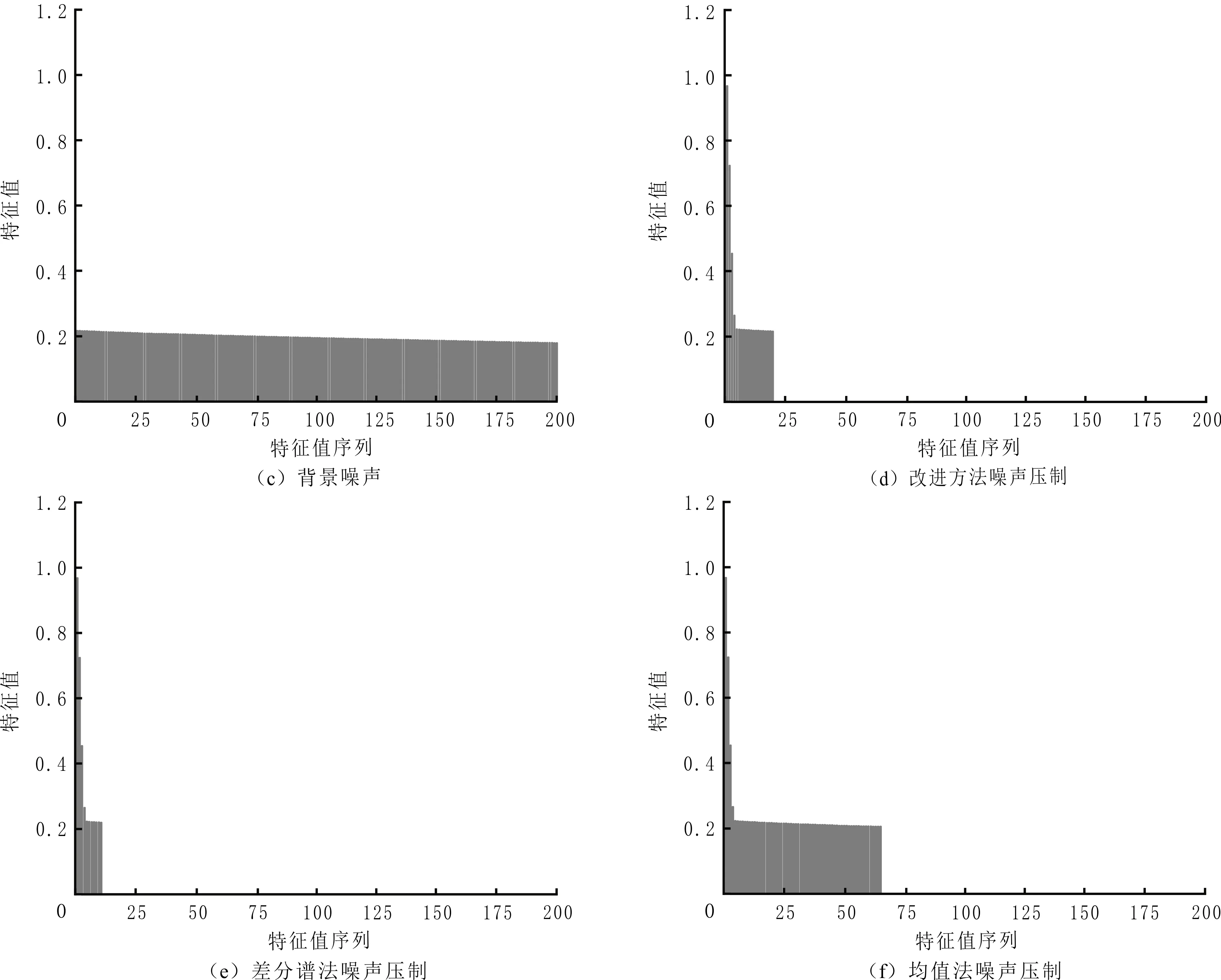
图3 三种方法特征值序列Fig.3 Eigenvalue sequence of three methods

3 微地震资料处理

3.1 应用一

为验证基于背景噪声和特征值下降比的微地震SVD去噪改进方法可行性，采用松辽盆地某一地区某页岩油水平井实际压裂时微地震三分量检波器监测的数据，进行噪声压制处理。该井处于扶余油层薄互致密油储层，压裂水平段测深为2 025.0～2 895.0 m，垂深为1 789.7～1 794.2 m。选取第7段射孔微地震监测数据，为显示各道数据的相关性和去噪结果，从三分量检波器选取11道数据进行测试，时间采样间隔为2 ms，每道为3×104个采样点。实际微地震资料应用一处理结果见图4，其中原始微地震数据见图4(a)，能够看到噪声较强，实际压裂采集的微地震数据见图4(b)，选取压裂结束后的微地震监测背景噪声提取噪声特征值；改进方法处理结果见图4(c)，去除噪声处理后，噪声得到压制，有效信号凸显(见图4(d))。即使在噪声较强的情况下，采用改进方法也可以有效压制实际资料的随机噪声，采用差分谱法噪声压制的数据见图4(e)、噪声见图4(f)。由图4(f)可以看到部分有效信号，表明当噪声较强时传统方法容易损害有效信号，采用均值法噪声压制的数据见图4(g)、噪声见图4(h)。由图4(c、e、g)可以看到，改进方法处理效果较好，能够有效提高分辨率。

3.1.1 微地震数据特征值分析

三种方法数据特征值选择分析见图5，其中灰色面积为微地震数据的特征值，实际微地震数据的特征值序列与添加模拟噪声的相比更加复杂。改进方法特征值选择分析见图5(a)，其中蓝色面积为背景噪声特征值，红色线为背景噪声最大特征值，黑色折点线代表前后特征值下降比，可以看到改进方法的约束条件更多，对有效信号损害程度也较小。对比差分谱法(见图5(b))和均值法(见图5(c))特征值选取，二者更易导致过降噪和噪声压制不足。

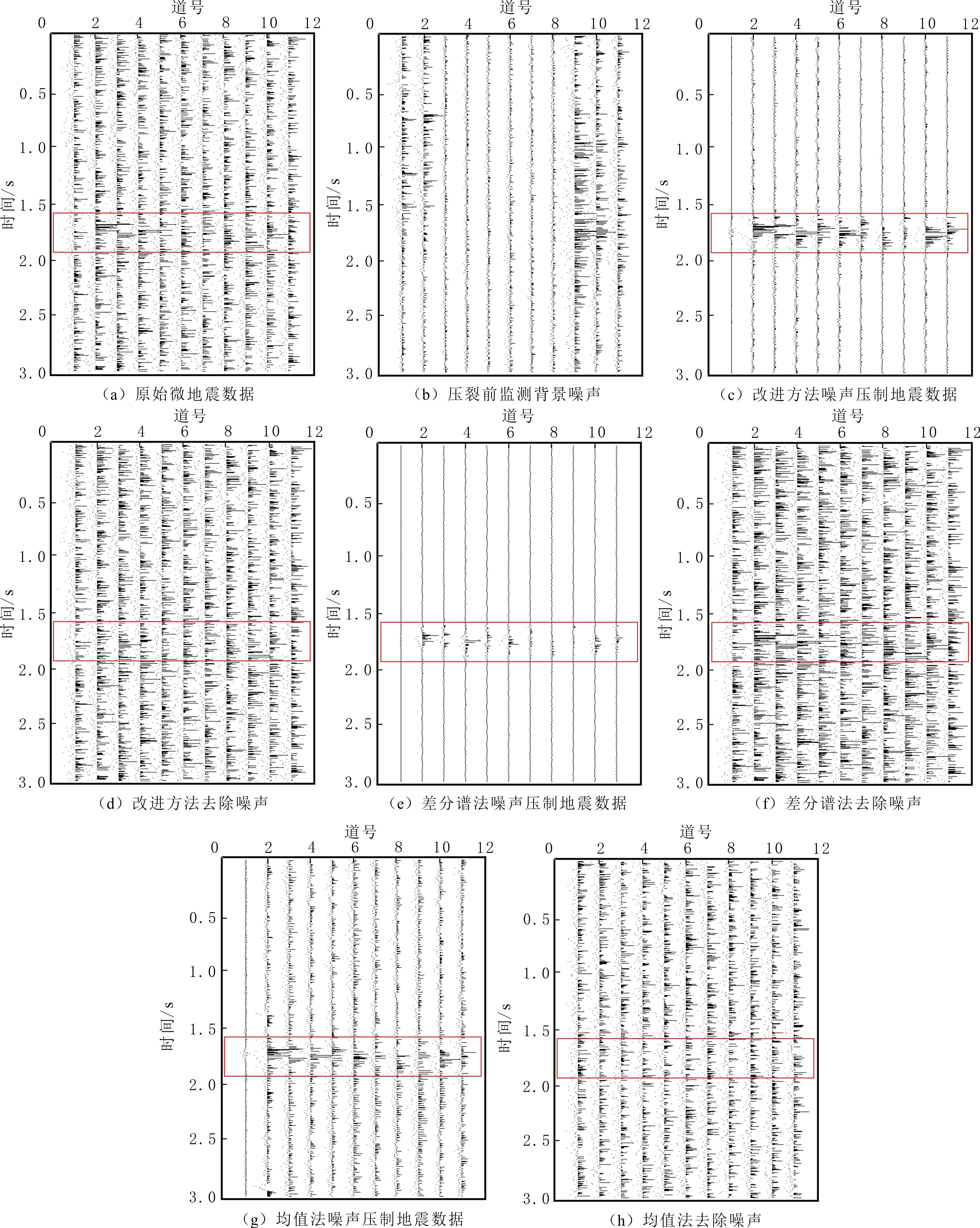
图4 三种方法实际微地震资料应用一Fig.4 Application of three methods to microseismic data 1

3.1.2 数据特征值序列

三种方法数据特征值序列见图6。为显示变化趋势，只选取部分特征值进行分析，其中图6(a-e)分别对应图4(a-c、e、g)各阶段数据的特征值序列。由图6(a)可以看到，多数有效信号数据的特征值集中于前半段，少数特征值分布在后半段，但噪声部分的奇异值存在范围较大，在实际数据处理中，噪声和信号的特征值混迭在一起。

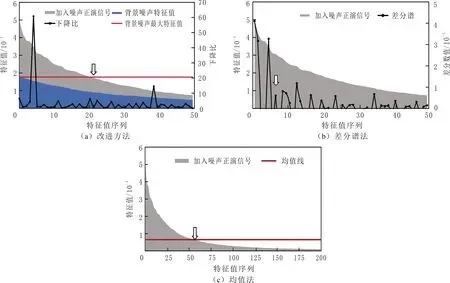
图5 三种方法数据特征值选择分析Fig.5 Analysis of three methods eigenvalue selection

差分谱法只选取前一部分特征值序列(见图6(d))，易产生过降噪或去噪不足。低信噪比时，有效信号淹没在噪声中，数据处理通常损害有效信号，对资料后期处理产生较大的影响。均值法选择特征值过多(见图6(e))。由图6可以看到，改进方法效果较好。

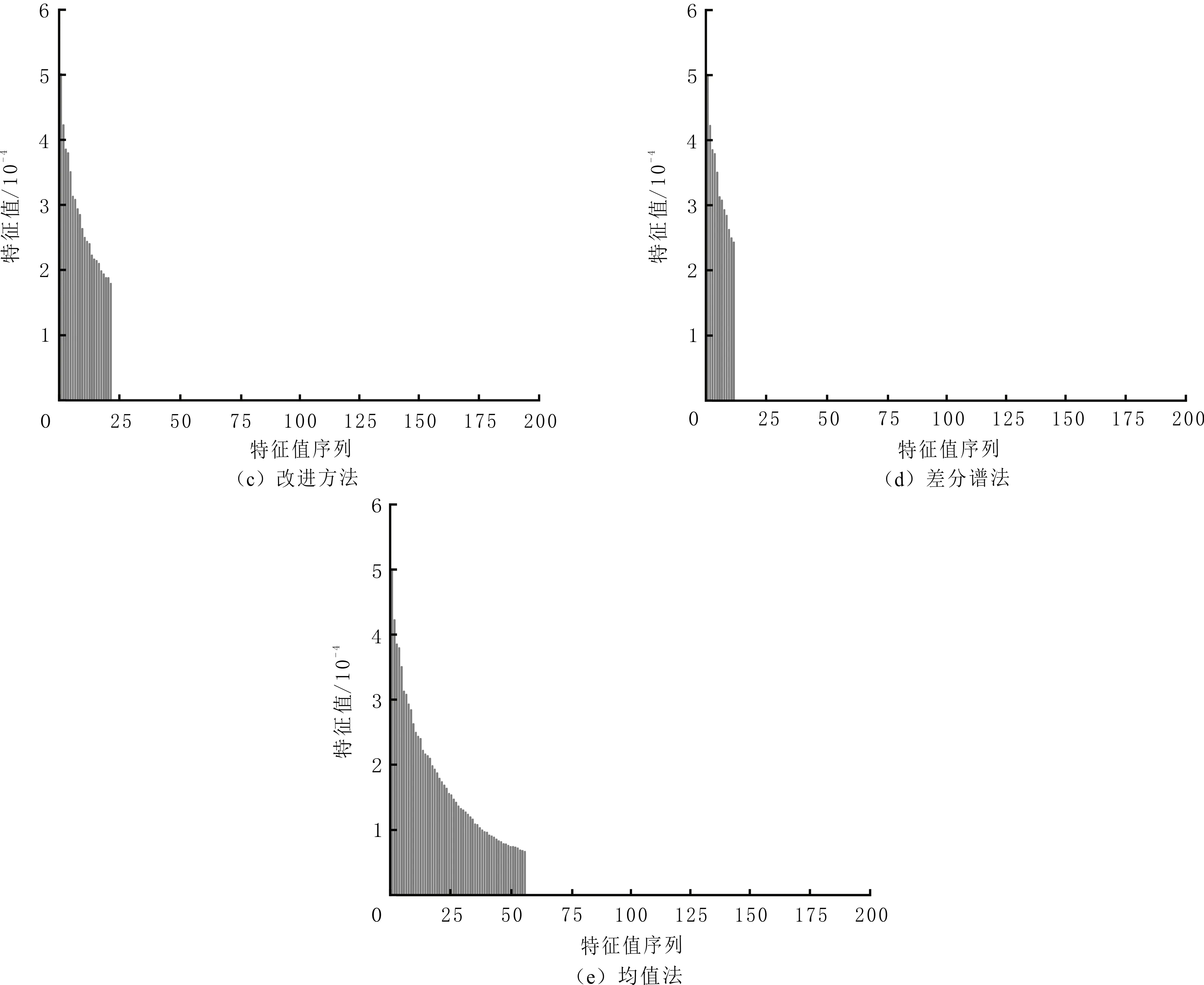
图6 三种方法数据特征值序列Fig.6 The field data eigenvalue sequence of three methods

3.2 应用二

为验证文中改进方法可行性，选取松辽盆地某一水平井实际压裂施工时、通过微地震监测技术采集的第6段地面微地震压裂监测数据。该井位于扶余油层薄互致密油储层，压裂水平段测深为 2 765.0～3 418.0 m，垂深为2 432.3～2 444.3 m。选取该井第6段实际压裂微地震监测数据，测试数据共有80道，时间采样间隔为2 ms，每道为3.0×104个采样点。第6段地面微地震实际监测数据地震记录见图7(a)，分别采用均值法、改进方法和差分谱法噪声压制的地震记录见图7(b-d)，对比改进方法处理前、后微地震数据，大部分随机噪声从数据中被去除，观察到肉眼可识别的大量的微地震信号，信号特征较为明显。与均值法和差分谱法效果对比，改进方法可以有效去除微地震资料中的随机噪声。

为考察三种方法对有效信号波形特征的影响，在原始数据(见图7(a))、均值法(见图7(b))、改进方法(见图7(c))、差分谱法噪声压制结果(见图7(d))中抽取单道进行对比，结果见图8，其中黑色地震波形为原始数据，对比均值法(蓝色波形)与差分谱法(绿色波形)可以看到，改进方法较好保留有效信号的振幅能量，噪声去除较合理，初至信息前的噪声压制较好、较平滑，保留整个有效信号区域。相应的数据频谱见图9。由图9可以看到，对比原始数据频谱，改进方法有效信号频带未发生迁移，噪声频率成分的能量得到压制，有效信号频带能量得到增强。

图7 某水平井压裂数据噪声压制地震记录Fig.7 Noise suppressing seismic record of fracturing data in a horizontal well

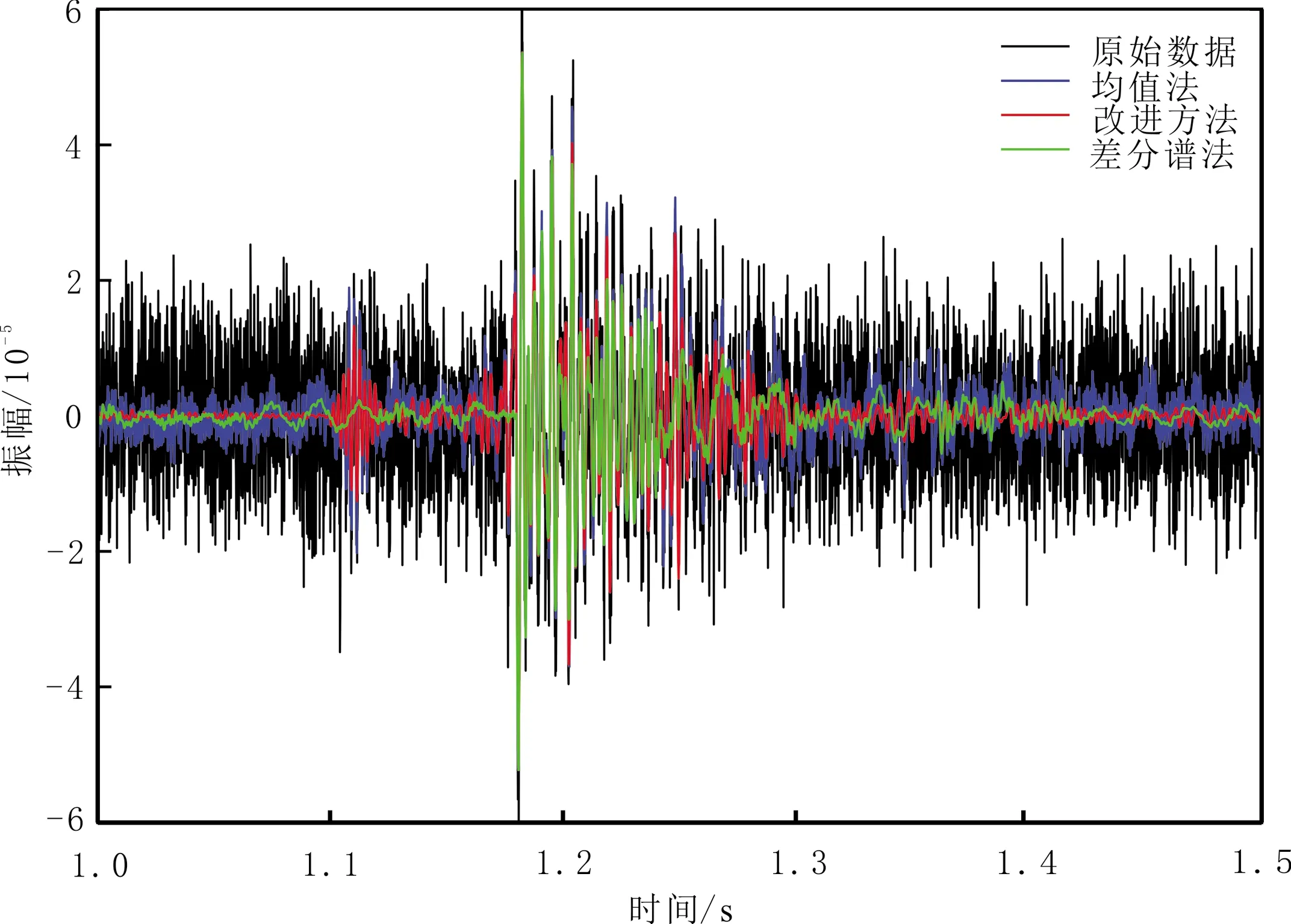
图8 三种方法单道数据处理结果Fig.8 Single channel data processing by three methods

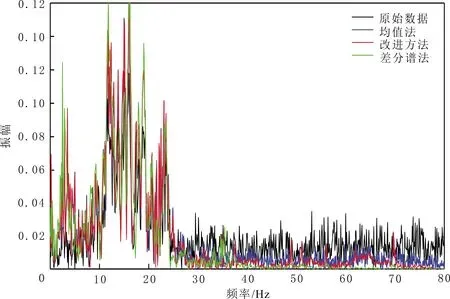
图9 三种方法数据频谱Fig.9 Spectrum comparison of three methods

4 结论

(1) 基于背景噪声特征值与特征值下降比改进奇异值有效阶次方法，利用背景噪声特征值确定范围，根据特征值下降比进行有效阶次选择。

(2) 文中改进方法有效压制低信噪比数据中的随机噪声，有较好的噪声压制效果，能够保留有效信号的能量和频率信息，为后续处理提供依据，具有可行性及有效性。