基于SAS软件对1985-2004库欣现货交易的原油价格的时间序列分析

周泽海

【摘 要】本文使用SAS软件根据现有的1985年1月至2004年12月原油现货价格数据，判断该序列的平稳性，探究自相关系数偏自相关后使用最为适合的ARIMA模型拟合序列的发展。

【关键词】时间序列分析;能源价格;ARIMA模型;原油价格;SAS软件应用

一、引言

原油作为人类社会中十分重要的能源，其有着工业的血液之称。目前有关原油价格的研究有[1]黄燕燕的论文，其使用奇异谱分析的时间序列分析方法研究原油价格的波动规律、未来走势、风险预警等。[2]文华的论文其使用了时间序列分析中的VaR-GARCH模型对原油期货价格进行分析。[3]周明磊的论文，分析了国际原油价格受事件的影响，文章主要使用ARMAX时间序列模型。本文主要利用ARIMA模型对1985-2004库欣现货交易的原油价格进行时间序列分析。

二、数据来源与数学建模

1、数据来源：本文使用1985-2004库欣现货交易的原油价格，数据来源于《应用时间序列分析》王燕（第四版）共有240个数据。

2、数学建模

首先我们要探究序列的平稳性（宽平稳性）。即序列无趋势性无周期性。宽平稳的数学建模如下。

ARIMA即为将序列进行差分运算后使用ARMA模型拟合，ARIMA的模型如下

三、數据分析

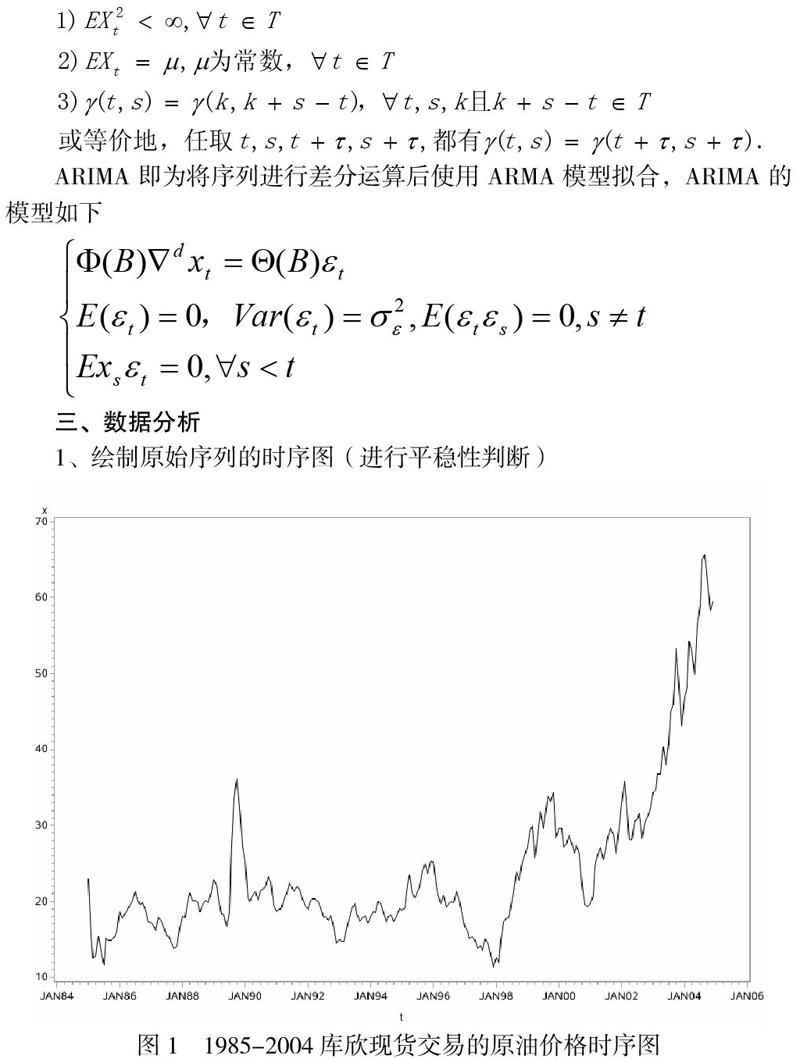
1、绘制原始序列的时序图（进行平稳性判断）

图1是1985-2004库欣现货交易的原油价格的时序图，可以看到整体的序列并不平稳，存在明显的线性趋势性。并且该序列的总体波动落差较大。综上所述，原序列不平稳，对其取一阶差分后平稳。

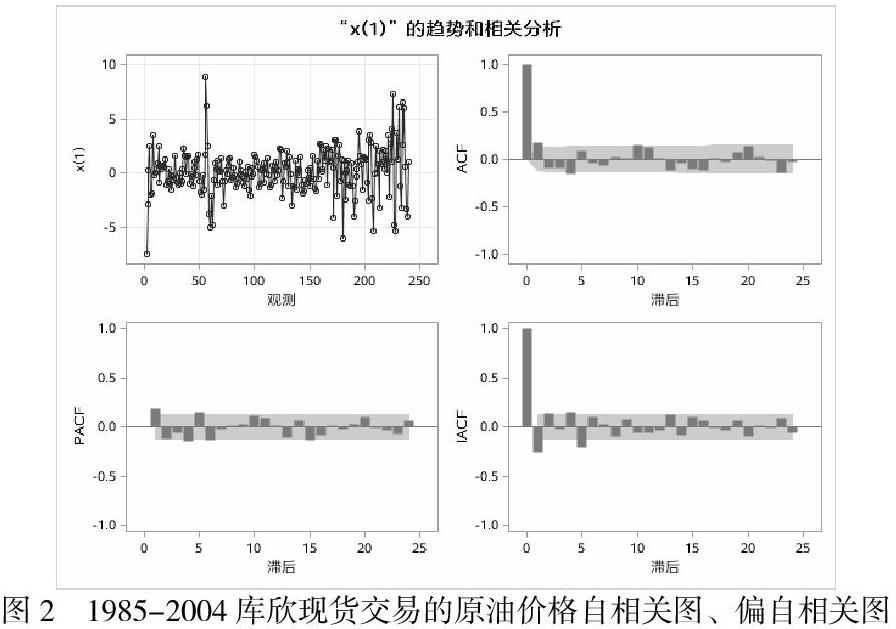
2、分析一阶差分序列的PACF与ACF选择最合适的ARIMA模型。

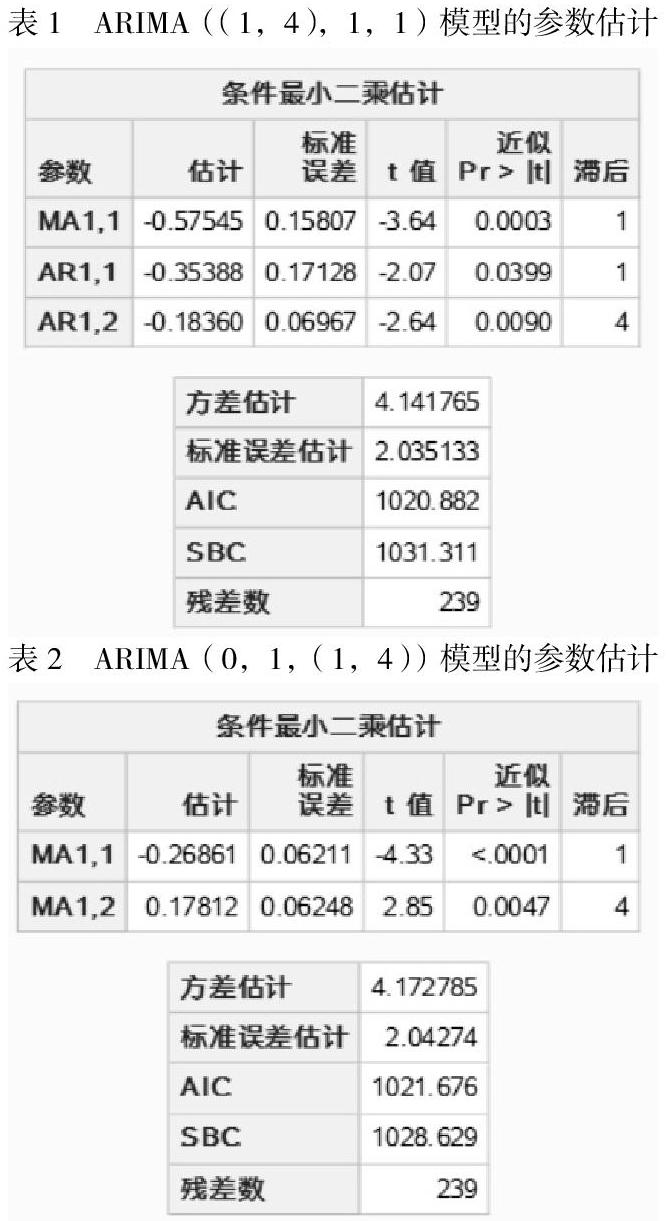
根据上述图2我们发现偏自相关系数在1，4阶截尾，自相关系数在1，4阶也截尾。并且都较为临界。所以我在尝试四种模型ARIMA（1，1，0）ARIMA（0，1，1）ARIMA（1，1，1）ARIMA（0，1，0）（随机游走模型）后都失败了（模型的残差白噪声检查未通过），于是开始拟合疏系数模型，在剔除存在不显著的系数的模型后尝试使用ARIMA（（1，4），1，1），ARIMA（0，1，（1，4））模型进行拟合，两者都不考虑常数项。以下的xt表示的是原序列，▽xt表示的是差分后的序列。

如表1与表2所示我们发现经过时间序列模型拟合，ARIMA（（1，4），1，1），ARIMA（0，1，（1，4））两个模型的各个系数都在0.05的显著性水平下显著。此外都通过了残差的白噪声检验（限于篇幅未列出）。即模型有效，但是从AIC准则看优先使用模型ARIMA（（1，4），1，1），综上所述1985—2004年原油现货价格的走势是震荡上升，对原油价格拟合ARIMA（（1，4），1，1）模型。最终拟合公式为：式中xt表示的是原序列，▽xt表示的是由于原序列不平稳，进行差分，B是延迟算子，表示残差序列。

四、结论

作为十分重要的能源——原油其价格也是收到了包括投资者、政策制定者、普通消费者的多方关注。对其进行研究十分有必要。本文使用SAS软件对1985-2004库欣现货交易的原油价格进行时间序列分析。结果表明1985—2004年原油现货价格的走势是震荡上升，使用ARIMA（（1，4），1，1）模型最为合适。

参考文献：

[1]黄燕燕. 基于区间时间序列多尺度分解的原油价格预测与风险预警管理研究[D].安徽大学，2020.

[2]文华. 基于VaR-GARCH模型的原油期货价格波动特征及风险研究[D].内蒙古财经大学，2017.

[3]周明磊.事件对国际原油价格影响的时间序列分析[J].数学的实践与认识，2004（08）：12-18.