两载流圆线圈间相互作用力与位置关系的探究

胡晓秋

(内江师范学院物电学院 四川 内江 641100)

1 引言

两平行载流圆线圈的探究一直是大学物理实验的重点内容，对其磁场分布的研究已经是一门成熟的教学演示实验课程．但在教学和论文研究中，对两平行载流圆线圈间的相互作用力的探讨却很少．文献[1]先用毕奥-萨伐尔定律求出磁场，再计算出两共轴圆形电流之间的相互作用力；文献[2]用一种迭代计算的方法，先计算出线圈之间的磁场再计算磁力；文献[3,4]是结合MATLAB利用虚位移的方法计算得出两线圈之间的磁力．上述方法中都对理论要求过高，计算过程可视化程度低，在教学中不适合教学推广．本文基于有限元仿真软件COMSOL中AC/DC模块，建立起两平行载流圆线圈的仿真模型．从两线圈之间位置关系出发，探究了当线圈位置关系从轴向平移、侧向平移以及旋转过程中磁力的变化．整个过程可视化程度高，对理论的要求低，在教学中容易引起学生兴趣，对掌握COMSOL仿真软件的仿真过程有较大的指导意义．

2 有限元仿真介绍

有限元仿真软件COMSOL Multiphysics(以下简称 COMSOL)最初源于 MATLAB 的 PDE Toolbox，是基于有限元的思想，专门用于求解偏微分方程的大型数值建模仿真软件[5,6]．针对不同的问题和研究领域，学者可以建立微分方程、设定边界条件，甚至利用各个模块进行叠加，实现多物理场的耦合；传统的仿真软件专业性强，要实现多物理场的耦合，需要利用各个软件的接口联接，同时仿真；物理场的微分方程也需要使用者自己编写；可见传统的多物理场耦合仿真方法程序复杂、效率低、结果不可靠和需要考虑软件之间的兼容问题；目前的工程仿真软件正朝着集成化方向发展，让仿真软件界面更加人性化，仿真流程效率更加高效，降低使用者的压力和节约时间．

2.1 有限元思想

有限元思想是从1943年开始萌芽，到1956年正式有文献提出有限元(finite element)术语，直至60—70年代完善理论框架，70年代开始将技术以软件的形式推向市场．其基本原理为将连续的系统离散化，然后对离散化的各个单元进行求解，最终整合各离散化参数对整个连续系统求近似解；通过其原理可知，要想对连续系统求解的近似值逼近真实值，就需加大离散的程度，离散的单元越多求解就越精确；但是随着离散化的加大，计算量也会剧增，对计算机性能提出更高的要求；同时离散化程度越高，进行求解时出现奇点的几率就越大，即计算结果不收敛；为解决这个问题就不得不依托各类算法，使有限元的计算更加智能．COMSOL 就是基于有限元理论的数值仿真软件，其求解器中已经内置各种有限元算法，可针对不同的求解问题进行选择；目前的大多数有限元仿真软件，都不需要用户调试算法，而是让用户更加集中精力解决仿真问题，这样仿真软件可以做的更加人性化，使用者的工作效率进一步提高；同时现有的计算机性能也越来越好，对利用有限元仿真软件计算更加庞大的系统提供条件，让有限元的应用更加宽广，到目前为止有限元仿真软件已经渗透到各行各业，例如飞机制造、桥梁设计、流体力学等领域．

2.2 多物理场耦合仿真软件应用领域

COMSOL是一款工程师使用较多的工程仿真软件，其核心产品如表1所示，包括模拟电磁、结构力学和声学等各领域和可供选择的27个模块．使用多物理场耦合软件的优势在于内部各模块可以单独使用，也可以多个模块之间任意配合，能对同一模型进行不同物理场仿真．COMSOL涉及的领域广，功能强大，这意味着科研工作者无论从事哪一领域的建模仿真工作，都可以遵循同样的建模仿真流程，降低仿真难度；COMSOL还开发与其他产品的接口，可以与通过LiveLinkTM接口与MATLAB，Excel，CAD，SOLIDWORKSD等软件联接，让仿真更加人性化．

表1 COMSOL Multiphysics 核心产品及模块

结合本文涉及的两载流圆线圈间相互作用力的仿真需要，选择AC/DC模块；AC/DC模块主要针对静电场、磁场及其他物理场的瞬态或稳态分析．

2.3 仿真模型的构建流程

利用COMSOL中进行仿真的流程图如图1所示．

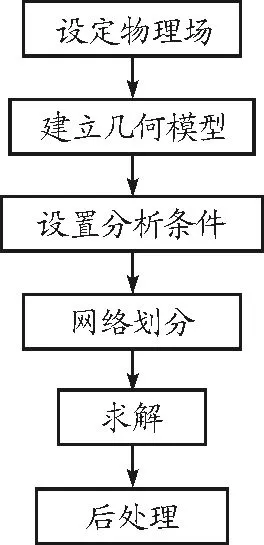
图1 COMSOL Multiphysics仿真流程

首先设定物理场，可以通过模型导向选择三维空间，物理场选择ACDC模块下的磁场(mf)，求解器选择稳态；建立几何模型是通过内置建模工具完成；设置仿真条件主要是对模型的域、边界进行磁场参数设置；网络划分是系统自动完成，为提高精度可人为修正；网络划分之后可利用求解器进行求解；最后将仿真结果进行后处理，得到需要的仿真数据．

3 两载流圆线圈间相互作用力与位置关系

3.1 同轴平行载流线圈之间的相互作用力与距离关系

同轴平行载流线圈之间平移的相互作用力与距离关系仿真图和关系图像如图2和图3所示.从图3我们可得出结论：随着两线圈间的距离不断增大，两线圈间的相互作用力的x分量的横向力一直不变，均为零，y分量的纵向力逐渐增大，尤其是当距离接近0.2 m时，y分量的纵向力相互作用力即增加得非常快了．

图2 同轴平行载流线圈之间平移的 相互作用力与距离关系仿真图

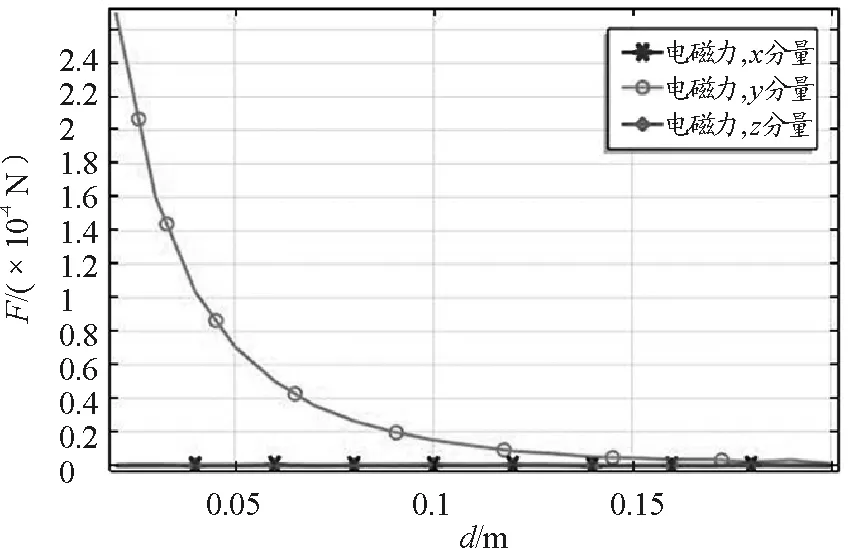
图3 同轴平行载流线圈之间平移的 相互作用力与距离关系曲线

3.2 平行载流线圈之间的相互作用力与侧向偏移距离的关系

仿真图和关系图像如图4和图5所示.从图5我们又可得出这样的结论：随着两线圈间的侧向偏移距离不断增大，两线圈间相互作用力的x分量的横向力先随着距离的增加而增大，到0.05 m时即5 cm时达到一个峰值，而后再随着两线圈间侧向偏移距离的增加而减小；当距离增加快接近8 cm的时候，力减小成了零，而后随侧偏移的增加而反向增大；但y分量的纵向力则一直随着两线圈间侧向偏移距离的增加而减小．而侧向力z分量的力一直不变，仍为零．

图4 同轴平行载流线圈之间侧向平移的 相互作用力与距离关系仿真

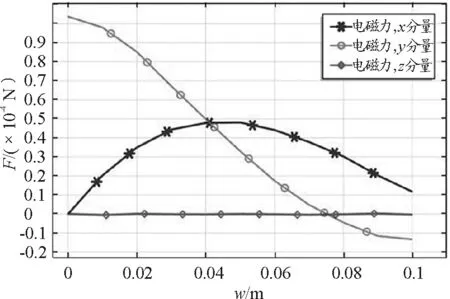
图5 同轴平行载流线圈之间侧向平移的 相互作用力与距离关系曲线

3.3 同轴载流线圈与偏转夹角的关系

仿真图和关系图像如图6和图7所示.

图6 同轴载流线圈与偏转夹角的关系仿真

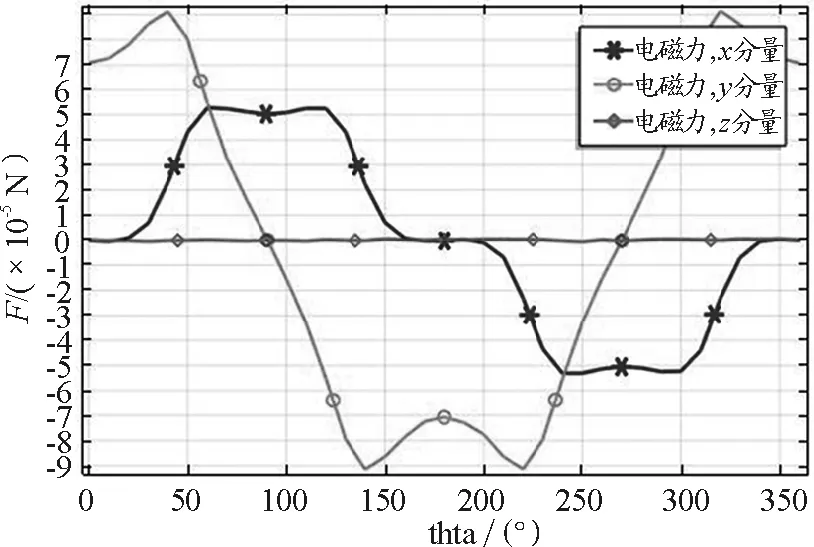
图7 同轴载流线圈与偏转夹角的关系曲线

从图7我们又可得出这样的结论：固定一个线圈的位置不动，让另一个线圈旋转，两线圈间的相互作用力x方向的横向力先随着旋转角度的增加而从零开始稍作迟疑后迅速地增大，在接近60thta到120thta时几乎达到一个稳定的状态，之后开始随着转角的增加x方向的横向力迅速减小至零，并在160 thta至200 thta一直保持为零，之后再随转角的增加x分量的横向力迅速反向增大，直到240thta至300thta又相对稳定下来，直到超过300 thta横向力又快速减小直到340 thta时x方向的横向力的再次下降为零，之后就一直保持为零了，在随着旋转角度增加的过程中x方向的横向力的大小关于零力线正好形成上下对称的图形，如图7所示.而y方向的侧向力则有所不同，当旋转角度为零时，y方向的侧向力一开始并不为零，而是约为7×10-5N，而后随着旋转角度增加侧向力缓慢的增加，至40 thta左右，约为9×10-5N，之后一直到90 thta，y方向的侧向力快速减小至零，而后又反向增加至-9×10-5N，之后再随着旋转角度增加至175 thta时侧向力缓慢地减小至-7×10-5N，形成一个小高点，而后又随之至220 thta左右侧向力反向增加至-9×10-5N，这以后再随着旋转角度增加直至260 thta左右，y方向的侧向力迅速减小至零，而后又正向迅速增大至旋转角度为320 thta时达到9×10-5N，之后再减小至7×10-5N；在随着旋转角度增加的过程中y方向侧向力的大小关于175 thta形成左右对称.而竖向力z分量的力在随着旋转角度增加的过程中一直保持不变，仍为零．

4 总结

本文采用有限元仿真软件建立模型的方法，分别研究了两载流圆线圈间相互作用力与位置改变的关系，分别从让同轴平行载流线圈平移.侧向平移以及旋转3个方面来探究两线圈之间相互作用力的变化．一方面利用COMSOL中AC/DC模块进行力学仿真探究，另一方面加深对两载流圆线圈间磁场力的直观理解．在教学中容易引起学生的兴趣，使学习效果得以提升.