无人机集群编队飞行研究

马文良

中国人民解放军92419 部队

无人机在军民各领域的应用越来越广泛，随着任务中目标的增多，仅依靠单架无人机已无法满足任务需求，与单架无人机相比，无人机集群编队飞行不仅可以有效降低成本，还可以提高无人机的利用率及执行任务的成功率，因此无人机集群编队飞行已经成为无人机应用的热点研究方向。本文对影响无人机集群编队飞行的因素进行分析，提出无人机集群编队飞行的计算方法，仿真计算结果表明，通过对无人机集群进行及时有效的控制，可以保证集群无人机完成编队飞行任务。

无人机集群编队飞行，即多架无人机进行某种队形排列进而满足任务要求的飞行方式。随着现代作战任务及电磁环境日趋复杂，仅仅依靠单架无人机完成任务的缺陷越发突出，无法保证执行任务的成功率，因此利用无人机集群编队飞行来执行复杂任务的需求越来越大。

从经济层面看，无人机集群编队飞行可极大提高复杂任务的执行成功率，进而有效降低成本；从利用率层面看，无人机集群编队飞行可以在一次飞行中完成多个任务目标，极大提升无人机的利用率。

但在实际飞行中，很多因素都将对无人机集群编队飞行造成影响，进而可能会对任务执行情况造成影响。本文对影响无人机集群编队飞行的因素进行分析，通过仿真计算，探寻如何在实际飞行中对无人机集群进行及时有效的调整，使无人机集群编队飞行能完成任务要求。

影响无人机编队飞行的因素

单架无人机从起飞到空中飞行，会受到多种因素的影响，进而对集群编队飞行造成影响。在此主要从无人机发动机启动方式、无人机外形结构、飞行控制器、飞行过程中环境因素及通信链路5方面，对影响无人机集群编队飞行的因素进行分析。

无人机发动机启动方式

无人机发动机有电启动、吹气启动等启动方式，不同的发动机启动方式所使用的配套设备不同，进而导致发动机启动所需的时间及成功率也不同。例如，当两架无人机发动机分别采用电启动与吹气启动方式时，由于吹气启动过程多了高压气瓶吹气中间环节，所以与电启动方式相比，发动机的启动时间较长，同时受到吹气设备可靠性的影响，发动机启动成功率要低，进而会对无人机集群编队飞行造成较大影响。

无人机外形结构

采用不同型号的无人机组成集群编队飞行时，由于无人机型号不同，外形尺寸与各型无人机的自身特性都会有较大差异。在执行任务前，技术人员根据任务要求对集群无人机的起飞方向进行合理规划，且在集群无人机起飞前，还需要考虑外界环境中的风以及不同型号集群无人机的抗风能力对起飞所产生的影响。当风速较大且超过集群无人机的抗风指标时，飞行任务会被取消；当风速较大且未超过集群无人机抗风指标，需要根据风向对集群无人机的起飞方向进行调整，这可能导致集群无人机偏离预定的起飞方向，进而对无人机集群编队飞行造成影响，如图1所示。

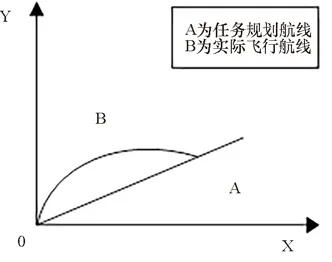
图1 集群无人机起飞段航迹。

飞行控制器

在集群无人机实际飞行过程中，由于不同型号的集群无人机飞行控制器存在能力差异，需要人工对集群无人机进行不同程度控制，任务执行情况也存在较大差别。如图2所示，当外界产生某种扰动时，如果集群无人机飞行控制器能力较强，自身可以及时对航线进行修正，进而快速回到任务规划的航线上；而如果集群无人机飞行控制器的控制能力较弱，就需要人工对集群无人机航线进行实时修正，这样就会大大增加集群无人机的调整时间，进而对无人机集群编队飞行造成较大影响。

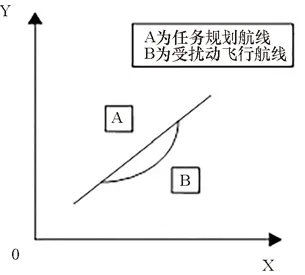
图2 集群无人机受扰动后飞行航迹。

飞行过程中环境因素

集群无人机在空中飞行时，环境大气密度的实际值与理论值之间存在的差异，会对集群无人机所受到的升力与阻力产生影响，同时会影响集群无人机发动机的效率，可能会使集群无人机偏离规划航线，从而对整体无人机集群编队的飞行造成影响。另外，由于环境中风速变化较大，可能会使集群无人机在转弯时无法按照预设航线进行转弯，导致集群无人机转弯偏离航线见图3，集群无人机的实际飞行航程增大，进而对无人机集群编队飞行造成干扰。

图3 集群无人机转弯航迹。

通信链路

在实际飞行过程中，受外界电磁环境影响，集群无人机可能会发生短时通信中断的情况。此时不但无法显示集群无人机的位置，同时也无法对集群无人机进行有效控制，若集群无人机在这段时间内受到扰动，会对集群无人机自身飞行造成影响，进而影响整体的集群编队飞行。随着集群编队中无人机数量的增多，对集群无人机通信链路的要求也越高，以减轻通信链路带宽不足可能带来的影响。

集群编队飞行的计算方法

无人机集群编队起飞后，经过爬升飞行到任务高度并进行一定调整后，开始进行无人机集群编队计算，流程如图4所示。具体计算方法，首先使用公式（1）计算长机与僚机之间的距离，然后与规定值进行比较，对僚机飞行速度进行调节，直到长机与僚机之间的距离满足约束条件。

图4 无人机集群编队飞行控制流程图。

计算两架集群无人机之间的距离：

其中，R为地球半径，（α1，β1）为长机当前坐标点，（α2，β2）为僚机坐标点。

假设在某次集群编队飞行任务中，长机A的当前坐标点为（α1，β1），僚机B的当前坐标点为（α2，β2），现要求长机A与僚机B之间的距离为2km，误差范围为0.1km （见图5）。

图5 无人机集群编队飞行。

保持长机A的飞行速度不变，对僚机B的飞行速度进行调整，利用上述计算步骤进行仿真计算，得出的仿真结果如图6、图7所示。最终两架集群无人机间距为2.004km，误差为4m，满足要求。

图6 两架集群无人机间距曲线。

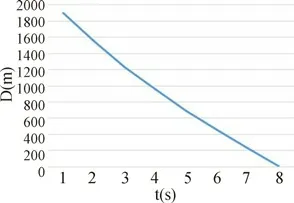
图7 两架集群无人机间距与约束条件差值曲线。

通过分析影响无人机集群编队飞行的5种因素，提出无人机集群编队飞行计算方法，并通过仿真计算证明，该方法能及时有效调整无人机飞行速度，在保证无人机成功执行集群编队飞行任务中发挥作用。