折纸的数学教学价值和实践探寻

王立成

[摘要] 厘清教材中折纸活动的编排特征，呈现折纸活动思维梯度，可以使得相应的教学活动开展得更加有层次、更加深入。作为一种学习手段，折纸活动不仅可以有效沟通教材新旧知识的联系，还可以丰富多种知识的学习途径，充实课堂教学内容。

[关键词] 折纸;教材;教学价值;教学探寻

在丰富多彩的折纸活动中，有许多数学活动值得我们去研究。通过折纸活动，分析留在纸张上的折痕以及折痕围成的图形，能够揭示出许多的几何的对象、性质、概念、规律、图形与图形之间的关系以及数与图形之间的关系，如：轴对称、中点、对角线、分数的意义等。在这些灵动、具体可视的过程中，弥补了学生思维的短缺部分，更能符合小学阶段学生的年龄特征和认知习惯。

苏教版小学数学教材在低、中、高年级都安排了折纸的活动，年级不同，教材上折纸活动的设计目的也有所差异。教材中折纸活动以怎样的形式存在？有怎样的教学价值？教学中如何利用好折纸活动更好地为课堂教学服务？折纸还有哪些新的开发价值？本文将对这些内容做一些思考与探寻。

一、教材的编排与教学要义分析

苏教版小学数学教材在12册书中安排了20次折纸活动，其中以例题呈现或者在例题中涉及折纸操作的有11次。从梳理教材内容可以发现，教材中折纸的内容有以下特点：

1.折纸的步骤由简单到复杂

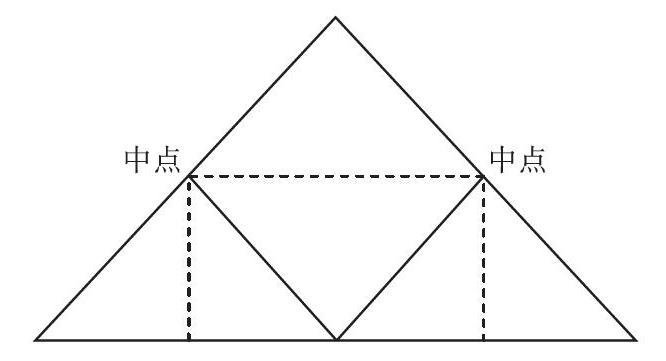
低年级的折纸操作大部分一步即可完成，随着年级的增长与折纸经验的积累，折纸的步骤不断变得复杂，由初始的一两步向四五步甚至更多、更复杂的情况延伸。最初的活动是个体独立进行，随着折纸复杂程度的提升可进行小组合作，如三角形的内角和（见下图）。

2.折纸的思维由低阶到高阶

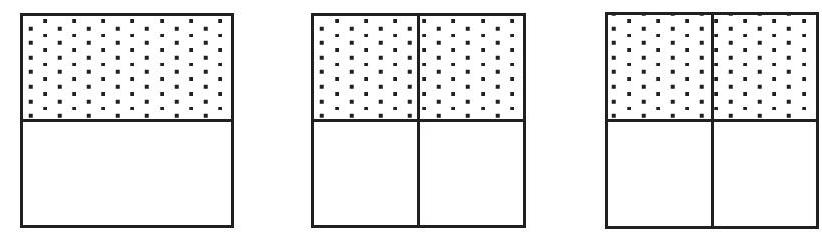
低年级的折纸操作比较直观、简单，只要按照要求，规范操作就可以。到了中、高年级，折纸之前要有全面细致的思考，在折紙的过程中，每一步都有思维的导向，所以折纸过程要求严谨、有序，如：分数的基本性质的探究过程就安排了下面的“折一折”教学活动。

师：像这样折一折、涂一涂，并用分数表示涂色部分。你有什么发现？

3.折纸的要求由感知到建模

教材中对折纸内容的要求也有一定的梯度。低年级的要求较低，主要目的是让学生对相关内容从操作层面有具象的感知，为进一步学习探究做铺垫，而对中高年级学生的要求就会指向数学模型的建立。

如：用长方形或者正方形纸折出二分之一，第一次折是为了初步感知和认识分数的概念;第二次折是为了比较异分母分数的大小，同时对分数做进一步认识;第三次折则是为了掌握分数的基本性质，建立相应的数学模型，突破原有的认识。

儿童的数学学习都是从懵懂走向清晰，从混乱走向有序，对折纸活动的深刻认识实则上是对儿童认知规律的认识，体现教师教学中的学生本位。每一次折纸，都伴随着观察、思考、交流、比较、概括等一系列活动，在这样立体的折纸活动场域中操作与思维相辅相成、共生共长。

二、折纸的教学价值

1.折纸呈现概念的形成过程

概念学习是小学阶段重要的学习内容之一，很多概念的形成都需要数次数学抽象参与，如果教师能通过巧妙的设计，让折纸活动渗透儿童概念学习的过程中，会让概念当中的抽象部分更加具体和直观，有利于学生对其理解和掌握。例如在学习轴对称图形一课时，学生对“轴对称”的概念比较生疏，很多学生对“轴对称”和“对称轴”这些概念容易产生混淆。如果教师能够借助折纸活动，提供一些学生熟悉的折纸素材，教学会取得更加良好的效果。

2.折纸蕴含数学学习的策略

美国著名教育家杜威认为：儿童学习要在“做中学”。他认为儿童不从活动中，而由听课和读书中所获得的知识是虚缈的。

小学阶段的学生在学习数学的过程中，由于其特定的身心特点，所以必须要有“玩”的成分。而折纸的操作活动就是在玩中学、在做中学，在折的过程中伴随着思维的生长。如在学习《长方形和正方形的特征》时，折纸完成之后，教师应引导学生观察比较，从边和角的角度归纳出长方形和正方形的边角特点。这里的操作目的不在于“折”，而是为数学思维架设一道桥梁。

3.折纸体现教学理念和思想

从心理学角度出发，小学阶段学生的思维以具体形象为主，随着年级和年龄的增长，抽象思维的成分在不断地增多，而具有折纸操作的内容符合学生的身心发展的特点和直观教学的原则。《义务教育数学课程标准（2011年版）》中明确提出“帮助学生积累数学基本活动经验，是数学教学的重要目标”，而数学基本活动经验是在做中积累起来的。折纸的活动可以使学生获得直接的数学学习经验，在一次次的亲历中理解数学、喜爱数学。但“折”只是形式，折的过程中所伴随的数学思想才是灵魂。折纸的所有活动都指向数学观察、推理、交流、抽象和归纳，最终建立数学模型，促进学生思维的发展。折纸就是在“做中学”，在做中体会数学的推理、抽象、概括，感悟数学的智慧和美。

三、教学实践的思辨与探寻

（一）教材有关折纸的逻辑顺序思辨

苏联教育家维果茨基认为：教学应着眼于学生的最近发展区，为学生提供带有难度的内容，调动学生的积极性，发挥其潜能，超越其最近发展区而达到下一发展阶段的水平，然后在此基础上进行下一个发展区的发展。

对新知的学习应该有一定的生活的和思维的经验作为基础，为了让学生达到“跳一跳，就能够得着”的目标，必须要给学生提供丰富的思维原材料，折纸同样如此。为了折纸成功，应该在活动之前有一定的数学思维活动作基础，否则折纸的活动就失去数学的意义。如在苏教版小学数学二年级教材中，让学生在长方形中折一个正方形，这样的要求在二年级显然偏高。因为要折出正方形，必须要在学习了正方形的边角特征以及充分认识了长方形和正方形之间的关系之后才可以，而这些内容教材上都是安排在三年级系统学习，显然这样内容应该后置。

（二）教学探究与思量

1.建设好教学前后的桥梁

折纸教学的难度是不断螺旋上升的，若处理得恰到好处，则有利于学生发展。折纸对不同年级学生有着不同的要求，前一年段的学习，不仅仅是为了解决本年段的知识性问题，也是为下一年段的学习做好准备。根据教材内容的编排特点，教学上应该将折纸分为以下三个阶段：

（1）初级阶段：折得规范

低年级的折纸操作比较容易，在教学的过程中，很多老师只关注学生折纸的结果正确与否而忽视了学生折的过程的规范性，而当折纸的活动越来越复杂，折纸过程的规范性就显得尤为重要。

（2）中级阶段：“折思并重”

相较于初级阶段的折纸，在中年段无论是折的要求还是折的步骤都要复杂很多，这就要求提高中年段学生折纸思维的参与度。折纸之前要思考好每一个环节，做到“思在前折在后”;折之后要反思折纸过程是否严谨规范，折纸结果是否正确合理。一言以蔽之，思维与操作每时每刻都是共同伴随的。

（3）高级阶段：折出模型

模型是数学内部世界与外部世界之间的桥梁，模型就是数学在解决问题的过程中思维活动的结果。折纸的重要目标之一是帮助学生建立数学模型，模型的建立同样需要丰富的经验积累。如在学习分数的基本性质之前，学生已经有了非常多的折纸经验储备，分数基本性质的教学其实就是学生将长方形纸通过折纸的方法，平均分成若干等分，经历观察、比较、抽象、概括后寻找关系建立的数学模型。

2.賦予折纸新的教学意义

一种生命力强的教学策略或者学习活动，应该具有以下的特点：操作简单、容易推广、使用范围广，具有科学性并蕴含着丰富的数学思想。折纸具备了上述特点，让每一个学生拥有充分参与思维活动的时空。那么折纸除了在教材中的几何图形的认识及分数等章节中的重要作用外，还可能有哪些特殊的应用呢？笔者在教学活动中做一些尝试性的探寻。

（1）折纸——平行四边形面积的再创造

教学路径的展开，有时教师可以独辟蹊径，通过不同的角度对教材内容进行改编，从而达到更好的教学效果。例如，教材中有关平行四边形的面积教学是借助方格纸来展开的，而普通的平行四边形因为其不具有轴对称性，在小学阶段折纸的内容很少涉及平行四边形，但是在学习平行四边形面积之前学生已经有了丰富的折纸经验，如果在此处向学生提供一些通过折纸得出平行四边面积的方法，不仅丰富了方法的多样性，还能沟通知识的前后联系，丰盈学生的思维过程，提升学生思维能力。

（2）折纸——直线位置关系的好帮手

古人云：“文似看山不喜平。”教师的课堂也应有波澜起伏，课堂教学的活动设计应该有动有静，动静结合才能达到较好的教学效果。例如，在学习直线间的位置关系时，教材并没有出现折纸的内容，仅仅以平面图形上线段的形式出现。但是笔者认为：给学生呈现的若只是静态的结果，所蕴含的思维价值是非常有限的。教师可以创设思维环境，把静态图形中的线段，加入折纸过程，让学生通过参与创造直线平行与垂直，最终理解直线间垂直与平行的关系及原因。

（3）折纸——数学课堂的调味剂

托尔斯泰说：“成功的教学所需要的不是强制而是激发学生的兴趣。”小学数学的课堂趣味性活动必不可少。由于小学生知识水平的限制，折纸在小学数学课堂中只发挥了极小的部分功能，但是数学教师可以适时向学生介绍一些折纸中比较有趣的方法和知识，使数学课堂更加丰富、有活力。例如：在学习立体图形时，教师可以介绍如何用正方形纸折出正方体;在学习量角时，教师可以介绍30°和60°角的折法，以激发学生学习数学的兴趣和思维需求。

根据教育心理学家皮亚杰的认知发展阶段理论，小学生的抽象思维水平较低，其思维层次在很大程度上处在形式逻辑思维阶段，辩证思维还处在萌芽和初始状态。因此，对概念的理解、判断、推理在很大程度上离不开直观手段的支撑，折纸让抽象知识“可视化”。折纸不是最终目的，折纸活动应该指向数学，应该有“数学味”，“数学味”就是对数、形的理解，适度抽象，进行更高层次上的“再实验”，帮助学生在活动中认识并改造自己的数学知识结构。折纸活动将零散的知识结构化、单一的图形模型化、抽象的思维显性化、静态的图形动态化，便于学生理解数学，建构新的认知结构。折纸活动作为多重价值的复合体，它在沟通思维与操作之间联系扮演着举足轻重角色，在教学上有更丰富的价值等待我们去发掘。一张白纸，蕴含无限“纸”慧！

[参考文献]

[1]中华人民共和国教育部.义务教育课程标准（2011版）[S]. 北京：北京师范大学出版社，2011.

[2]赵海庆.折纸与数学[M].北京：科学出版社，2007：34-36.