由折线算行程
左丁政
贴近生活的一次函数应用题备受各类考试命题者青睐,而有关一次函数图象的行程问题则更是各省市中考的一大热门.解决这类行程问题除了要把握好路程、速度、时间三者之间的基本关系,还要会由图象来获取信息,理清各变量之间的关系,根据题意选择适当的数学工具,通过建模解决问题.下面通过典型题目加以说明.
一、单人(或单车)直行
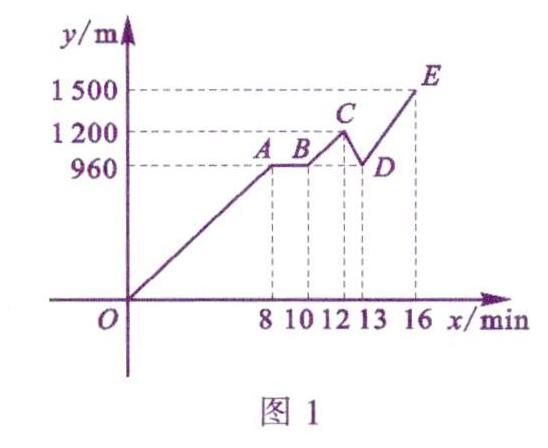
例1 周末,小峰骑共享单车到图书馆.他骑行一段时间后,在某一路口等红绿灯.当绿灯亮起来后他继续向图书馆方向前进,途中突然发现钥匙不见了,于是立即沿原路返回.他在等红绿灯的路口找到了钥匙,便折返继续前往图书馆.小峰离家的距离y (m)与所用时间x(min)的关系如图1所示,請根据图中提供的信息解答下列问题:
(1)小峰等红绿灯用了____min.
(2)在前往图书馆的途中,小峰一共骑行了多少米?
(3)求直线OA,DE的解析式.
解:(1)由图象可知,小峰等红绿灯用了10-8=2 (min).
(2) 1500+(1 200-960)x2=1 980.在前往图书馆的途中,小峰一共骑行了1980 m.
(3)直线OA的解析式为y=120x,直缎DE的解析式为y=180x-1 380.
二、两人(或两车)直行
例2在市中学生运动会800 m跑的比赛中,甲、乙两名运动员同时起跑.刚跑出200 m.甲不慎摔倒,但他又迅速地爬起来继续投入比赛,并取得了优异的成绩.图2表示甲、乙两名运动员所跑的路程y (m)与比赛时间x(s)之间的函数关系.根据图象解答下列问题:
(1)甲再次投入比赛后,他的速度是多少?
(2)甲再次投入比赛后,在距离终点多远处追上了乙?
三、两人(或两车)往返行
例3 为了提高学生的身体素质.某班举行了一次远足活动.老师将学生分成了男生组与女生组.女生组由A地匀速步行到B地后沿原路返回;男生组由A地匀速步行,经B地继续前行至C地后沿原路返回.两组同时出发.设步行的时间为th,两组与B地的距离分别为s.(km),S2 (km),图3中的折线分别表示S1,S2与t之间的函数关系.
(1)A,B两地之间的距离是____km,B,C两地之间的距离为 km.
(2)分别求男生组由A地出发首次到达B地的时间及由B地到达C地所用的时间.
(3)求图中线段MN所表示的S2和t之间的函数关系式,并写出自变量t的取值范围.
(3)根据题意,得M,N的坐标分别为(0.8,0)和(1,2).由待定系数法知线段MN所表示的S2和t之间的函数关系式为S2=10t-8.自变量t的取值范围是0.8≤t≤1.
- 中学生数理化·八年级数学人教版的其它文章
- 用数学写就的名言
- 从勾股定理到佘弦定理
- 一道课本习题的变式研究
- “算两次”思想的妙用
- 二次根式如何比较大小
- 勾股定理的常见应用

