小小杠杆用处大
张咏梅


杠杆的使用或许可以追溯到原始社会,当原始人拾起一根棍棒与野兽搏斗,或用它撬动一块巨石时.他们实际上就是在使用杠杆,石器时代人们所用的石刃、石斧,都用天然绳索将它们和木柄捆束在一起.或在石器上凿孔,装上木柄,这表明他们在实践中懂得了杠杆的经验法则:延长力臂可以增大力量.
那么,到底什么是杠杆?什么是力臂?为什么使用杠杆可以省力呢?
认识杠杆
杠杆是我们在生活中经常用到的工具,在初中物理教材中把杠杆定义为一根在力的作用下可以绕固定点转动的硬棒,硬棒可以是任意形状的.这点在生活中的表现比较明显,如剪刀、扳手、撬棒、钓鱼竿等都是杠杆.
如图1.杠杆需要具备五方面要素:支点、动力、阻力、动力臂、阻力臂.其中支点是杠杆绕着转动的点.动力指使杠杆转动的力.阻力是阻碍杠杆转动的力.动力臂是从支点到动力作用线的距离,阻力臂是从支点到阻力作用线的距离.
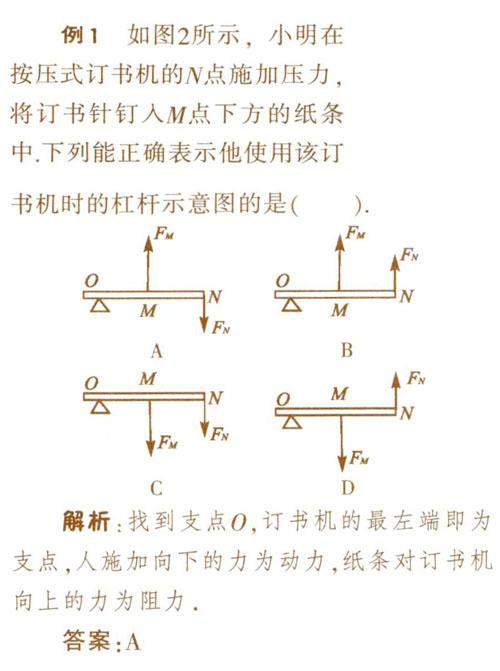
例1如图2所示.小明在按压式订书机的N点施加压力.将订书针钉人M点下方的纸条中.下列能正确表示他使用该订书机时的杠杆示意图的是( ).
解析:找到支点O.订书机的最左端即为支点,人施加向下的力为动力,纸条对订书机向上的力为阻力.
答案:A
力臂的概念及画法
我们使用的杠杆各有不同,主要的区别在于动力臂和阻力臂的大小不同,从支点到动力作用线的垂直距离叫动力臂,通常用l1表示:从支点到阻力作用线的垂直距离叫阻力臂,通常用l2表示.
力臂的画法(图3):(1)首先根据杠杆的示意图.确定杠杆的支点.(2)确定力的作用点和力的方向,画出力的作用线.(3)从支点向力的作用线作垂线,支点到垂足的距离就是力臂.(4)用字母l.或l2标出.
倒2 图4为钓鱼竿钓鱼的示意图.O为支点,画出F1、F2的力臂l.和l2.
解析:已知支点O.从支点向F1的作用线作垂线,垂线段的长度即为动力臂l1;从支点向阻力F2作用线引垂线,垂线段的长度即为阻力臂l2.
答案:如图5所示.
点评:解决此类作图题,需要掌握力臂的概念.知道力臂是指从支点到力的作用线的距离(若图中画出动力、阻力的示意图,那么示意图所在的直线就是力的作用线,可以用虚线适当延长.若图中没有画出动力、阻力的示意图,可先依据题意画出力的示意图).
作图时我们要注意:
(1)力臂是从支点到力的作用线的距离,不是从支点到力的作用点的长度.
(2)力的作用点不变,力的方向改变时,它的力臂一般要改变.
(3)力臂可能与杠杆重合.杠杆的平衡条件
阿基米德的那句“给我一个支点我能撬动地球”铿锵有力,是什么使得这位伟大的科学先驱说出了这样的话呢?他说的就是杠杆原理.杠杆原理的应用虽然可以追溯到很早以前的石器时代,但是提出和论证杠杆原理.是由阿基米德在《论平面图形的平衡》一书中首先提出的.
杠桿的平衡条件是:动力×动力臂=阻力×阻力臂,用公式表示为F1l1=F2l2,这个平衡条件也就是阿基米德发现的杠杆原理.
根据杠杆平衡条件可知.当阻力和阻力臂的乘积一定时,增加动力臂,可以减小动力。
例3 图6a所示的杠杆是水平平衡的.如果在支点两侧的物体下方分别加挂一个等重的物体,如图6b所示,则杠杆( ).
A.右端下沉
B.左端下沉
C.要保持平衡应将左端的物体向右移动
D.要保持平衡应在右端再加挂一个物体
解析:设一个钩码重为G.杠杆一格长为L.a图杠杆平衡是因为2Gx2L=Gx4L.b图中杠杆两侧分别加挂一个等重的物体后(为便于研究,设物体的重也为G),左边力与力臂的乘积为3Gx2L,右边力与力臂的乘积为2Gx4L.因为3Gx2L<2Gx4L,即右边力与力臂的乘积较大,所以杠杆不能平衡,右端下沉,故A正确,B错误.若想让杠杆能够平衡.可以将左端的物体向左移动,从而增大左边的力臂,使左边的力与力臂的乘积等于右边的力与力臂的乘积,或在左端再加挂一个物体,左边的力变大,使左边的力与力臂的乘积等于右边的力与力臂的乘积,故C、D错误.
答案:A
学即用,练一练
(2019.自贡)如图7所示,轻质杠杆的A点挂一重物G,绳受到的拉力为F2,D为杠杆的支点.请在杠杆的端点B处画出使杠杆保持静止的最小的力F1的示意图,并作出F2的力臂l2
答案:如图8所示.
- 中学生数理化·八年级物理人教版的其它文章
- 数理化是基础
- “简单机械”学习指要
- 滑轮自述
- 厘清“功率”与“效率”
- 杠杆的分类和应用
- 熟悉而又陌生的摩擦力

