盾构隧道下穿砌体结构房屋影响因素敏感性分析
李梓亮 汤劲松 赵书银


摘 要:为探究不同影响因素对盾构隧道下穿砌体结构房屋的影响程度,采用正交试验方法对5 种不同影响因素进行 5 种水平正交试验,通过MIDAS-GTS 有限元软件建立砂土地层-隧道-建筑物共同作用的三维分析模型,根据盾构隧道下穿砌体结构房屋施工过程中墙体所受到的最大拉应力增量,判断各影响因素对盾构隧道下穿砌体结构房屋的影响大小。研究结果表明,隧道轴线与建筑物中心线间距是盾构隧道下穿砌体结构房屋的最主要影响因素,其他依次为建筑物长度、隧道轴线与建筑物中心线夹角、隧道埋深,地层类型对砌体结构房屋的影响最小。
关键词:地铁;盾构隧道;下穿建筑物;砌体结构;影响因素;正交试验
中图分类号:U455.43
1 引言
研究不同影响因素在盾构隧道施工过程中对砌体结构房屋的影响是目前地下工程领域的主要研究方向之一,对实际工程具有重要意义。朱才辉[1]运用ANSYS研究了地铁隧道施工对西安黄土地层变形的影响规律,分析了建筑物刚度、基础埋深以及偏心距等因素对地表沉降的影响;丁祖德等[2]采用MIDAS-GTS对地铁隧道以不同角度下穿独立基础建筑物时,建筑物基础的沉降及建筑物的扭曲变形进行了分析;张立茂等[3]利用卡方关联分析方法和灰色关联算法分析了隧道相关因素、岩土层物理性能因素、盾构施工因素和建筑物因素对建筑物变形的影响,结果表明盾构施工因素和建筑物因素为主要影响因素;王俊等[4]采用三维离散元方法研究了隧道埋深对砂土地层地表沉降的影响规律,结果表明当隧道埋深大于2倍隧道直径时,隧道上方会形成稳定的塌落拱;魏纲、赵淑芹、孙宇坤等 [5-7]将基础局部倾斜作为评价盾构隧道下穿砌体结构房屋影响大小的标准,但不足之处在于基础的局部倾斜并不能直接反映出盾构隧道施工对上部砌体结构房屋所造成的影响,也不能判断整个施工过程中建筑物结构的安全性。
虽然目前已有的文献对盾构隧道下穿建筑物影响因素的研究相对较多,但主要以单因素下的多水平研究为主,并且主要以地表变形作为评价指标,而对盾构隧道施工过程中影响地表建筑物(特别是多层砌体结构房屋)的因素进行系统研究鲜见报道。为此,本文对盾构隧道下穿砌体结构房屋过程中的设计因素进行研究,采用正交试验方法,分析5种不同设计因素在盾构隧道下穿过程中对砌体结构房屋的影响规律,以墙体最大拉应力增量作为评价指标,判断各因素对建筑物的影响程度,并找出其中的主要因素。
2 正交试验设计
2.1 试验评价指标
对于砌体结构房屋而言,其对地基的不均匀沉降十分敏感,不均匀沉降会导致砌体结构墙体发生挠曲,从而引起砌体承重结构开裂,尤其在墙体窗户、门洞等建筑物刚度相对较小的部位。为更好地探究盾构隧道施工给砌体建筑物带来的影响,本文选取砌体结构房屋的墙体作为研究对象,以盾构隧道施工过程中墙体所受到的最大拉应力增量为试验评价指标,同时采用MIDAS-GTS对正交试验方案进行数值模拟计算,并对试验结果进行分析,从而得到影响因素的主次顺序和优化方案。
2.2 影响因素及水平
盾构隧道下穿建筑物影响因素分为设计因素和施工因素2类,其中,设计因素主要包括盾构隧道轴线与建筑物的夹角、隧道与建筑物的相对位置、隧道埋深、建筑物刚度、地层类型、盾构隧道直径、隧道上部荷载和地下水位等。
对于盾构隧道轴线与建筑物的夹角、隧道埋深和地层类型这3种因素,可以直接采用岩土工程软件进行模拟;对于建筑物刚度因素,通过调整建筑物的长度实现建筑物刚度的变化;对于盾构隧道直径因素,由于城市地铁隧道多为单线隧道,且设计直径相差不大,故忽略其影响;对于隧道上部荷载因素,在盾构隧道下穿建筑物过程中,其荷载组成主要为建筑物荷载,所以通过调整隧道与建筑物的相对位置可以实现隧道上方荷载的变化,故将隧道上部荷载因素归入隧道与建筑物相对位置因素中;对于地下水位因素,由于其不确定因素较多,本文不对其进行相关研究。
为此,本文从上述设计因素中选取5个典型因素进行正交试验分析,其分别为地层类型、隧道埋深、建筑物中心线与隧道轴线距离、隧道轴线与建筑物中心線夹角以及建筑物长度。
(1)地层类型。选取砂土地层作为研究对象,将砂土分为5类,按颗粒大小分为砾砂、粗砂、中砂、细砂、粉砂[8]。
(2)隧道埋深。选取的隧道埋深分别为1.5D、2D、2.5D、3D、3.5D,其中D为隧道开挖直径,为6.44 m,下同。
(3)建筑物中心线与隧道轴线间距(以下简称“水平间距”)。取建筑物中心线与盾构隧道轴线之间的间距为研究对象,取5个水平,分别为0、1D、2D、3D、4D。建筑物中心线与隧道轴线间距为1D时,建筑物与盾构隧道的相对位置关系如图1所示。
(4)建筑物中心线与隧道轴线夹角(以下简称“夹角”)。将建筑物中心线与隧道轴线的夹角从0°~90°均分为5等份,分别为0°、22.5°、45°、67.5°、90°。建筑物中心线与隧道轴线夹角为22.5°时,建筑物与隧道的相对位置关系如图2所示。
(5)建筑物的长度。选取建筑物开间3 m、进深5.1 m的房间为基本单元,通过增加建筑物基本单元房间来实现建筑物长度的变化,本文取18 m、24 m、30 m、36 m、42 m5个建筑物长度,18 m长砌体结构建筑物如图3所示。
将上述各影响因素及其水平进行汇总,其中水平分为中砂、粉砂、砾砂、粗砂、细砂5个水平,如表1所示。
3 数值模拟方案
3.1 模型建立原则
正交试验过程中会涉及不同条件下的侧穿、下穿建筑物等工况,为此,在建立三维模型时采用以下原则:
(1)模型长度取隧道左右各6D,且满足建筑物边缘与模型边缘距离不小于30 m;
(2)模型宽度取模型的外边缘离建筑物的最小距离不小于30 m;
(3)模型高度,隧道以上取至地表,隧道以下取 3D;
(4)建筑物墙体只开窗洞,不开门洞。
地层为粉砂、隧道埋深1.5D、水平间距 D、夹角为 22.5°、建筑物长36 m时,三维数值模型如图 4所示,模型尺寸为86 m×57 m×49 m。
3.2 地层参数确定
考虑到隧道的开挖卸载作用,本文对地层的本构模型选用摩尔库伦和修正摩尔库伦2种土的本构,从地表至建筑物基础下方0.5 m处采用摩尔库伦本构关系,其余土层采用修正摩尔库伦本构,修正摩尔库伦本构模型中卸载模量取3倍的弹性模量[9-10],地层参数如表2所示。
3.3 材料参数确定
盾构机刀盘直径6.44 m,盾尾间隙95 mm。盾构隧道管片采用C50预制钢筋混凝土管片,管片外径6.2m,内径5.5 m,宽1.5 m,管片采用螺栓进行连接。盾构机、管片以及注浆材料统一采用线弹性模型,考虑到管片接头的拼装,将管片的刚度按0.85的系数进行折减[11]。注浆浆液考虑软注浆液和硬注浆液2种,在隧道开挖5环后将软注浆液硬化为硬注浆液[12]。材料参数如表 3所示。
3.4 建筑物参数确定
考虑建筑物为地上3层砌体结构,层高3 m,无地下室,墙厚240 mm;建筑物长度按表1中取值,宽5.1m,高9.3 m;基础形式为条形基础,宽0.6 m,埋深- 0.5 m;窗洞宽1.2 m,高1.5 m,窗台高0.9 m;建筑物楼板为现浇钢筋混凝土板,板厚0.1 m。建筑物参数如表4所示。
3.5 施工过程
盾构隧道施工过程模拟:①计算地层的初始应力状态,地层位移清零;②施加砌体建筑物,位移清零;③钝化隧道开挖土体,激活盾壳和支护压力;④钝化盾壳,激活管片和软注浆液,开挖5环后激活硬注浆液;⑤重复③~④至隧道开挖完成。
4 计算结果分析
正交试验表采用6因素5水平正交试验表进行设计,正交试验表及数值模拟计算结果如表5所示。正交试验结果的分析处理有直观分析和方差分析2 种分析法[13]。
4.1 直观分析
直观分析法也称极差分析法,是通过分析每个因素的平均极差来解决问题。所谓极差就是极大平均值减去极小平均值得出的差。根据极差,就能得出主要影响因素,以及最优方案和最危险方案。表6为施工过程中墙体最大拉应力增量极差分析结果,表6中Ki为影响因素水平为i时,所对应的计算结果之和;ki = Ki /s,s为任一列上各水平出现的次数;极差R = max{k1,k2,k3,k4,k5}- min{k1,k2,k3,k4,k5}。
由表6对正交试验结果的极差分析可知,盾构隧道下穿砌体建筑物过程中,建筑物中心线与隧道轴线的水平间距这一影响因素的极差最大,地层类型的极差最小;按各因素极差从大到小得出影响因素的主次顺序为:建筑物中心线与隧道轴线间距、建筑物长度、隧道轴线与建筑物中心线夹角、隧道埋深、地层类型。
为更直观分析各因素對墙体拉应力增量的影响趋势,根据表6极差分析结果作各因素对墙体最大拉应力增量直观分析图,如图5所示。
由图5中各因素对墙体最大拉应力增量趋势可知,当地层为粉砂、隧道埋深为1.5D、水平间距为 D、隧道与建筑物夹角为0°、建筑物长为42m时,建筑物墙体所受到的最大拉应力增量最大,为最危险方案;当地层为砾砂、隧道埋深为3.5D、水平间距为4D、隧道与建筑物夹角为90°、建筑物长为18 m时为最优方案。
4.2 方差分析
为确定试验结果差异是来自于不同影响因素相应水平的改变还是来自试验误差,取显著水平α = 0.05对施工过程中墙体最大拉应力增量进行方差分析。
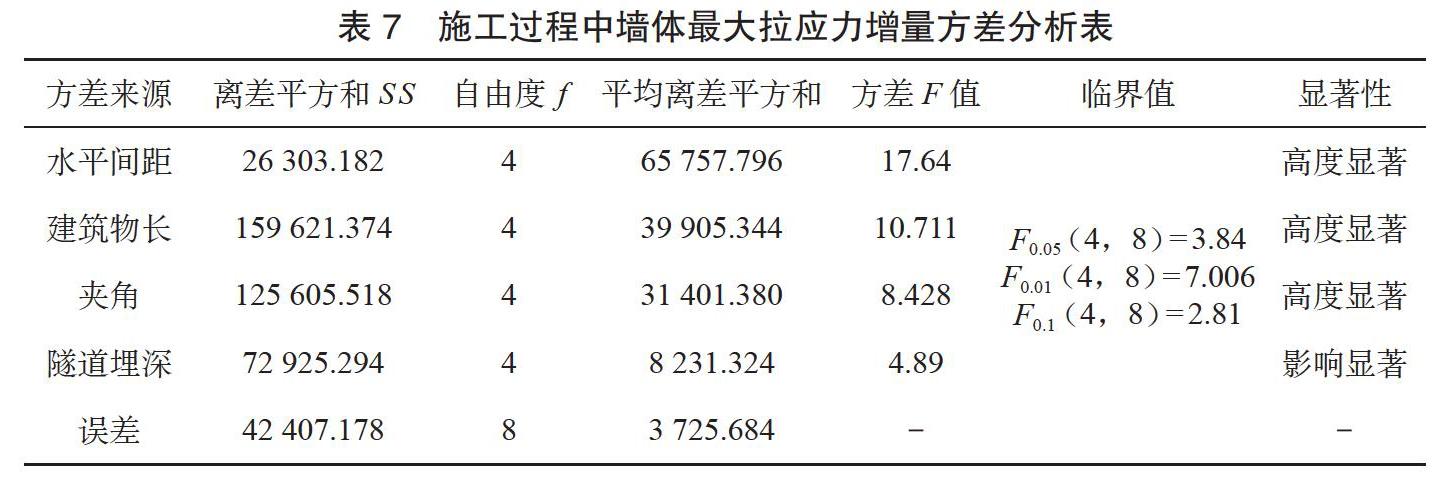
在对施工过程中墙体最大拉应力增量进行极差分析时,由于地层类型因素的均方小于误差的均方,所以将地层类型因素归入误差中,重新进行离差平方和、自由度以及均方的计算,形成新的误差,最终计算结果见表7。
根据表7试验结果方差分析和试验因素显著性分析可知,隧道轴线与建筑物中心线间距、建筑物长度以及建筑物与隧道夹角的方差F值均大于F0.01,表明这3个因素对试验结果有高度显著影响,为关键因素;隧道埋深的方差F 值大于F0.05,小于F0.01,对试验结果影响显著,为次要因素。该结论与极差分析的结果是一致的,进一步验证了极差分析中主次因素的正确性。
5 基于正交试验的方案优化及评价指标
5.1 方案优化
根据正交试验直观分析结果可以得出最优方案和最危险方案,由于最优方案不是下穿情况,所以对最危险方案进行分析。最危险方案计算得到墙体拉应力分布如图6所示。
从图6中可以看出,建筑物墙体拉应力分布总体上呈倒八字形,指向建筑物沉降最大位置处;然而建筑物拉应力最大的位置出现在窗户角上,与拉应力分布相反呈八字形,易形成八字形斜裂缝,此时建筑物墙体最大拉应力增量为687.687 kPa。
将最危险方案结果与正交试验结果进行对比,发现正交试验方案中墙体拉应力增量最大的试验编号为24,此时墙体拉应力增量为652.98 kPa,小于最危险方案中墙体的最大拉应力增量。对比试验编号24中各影响因素的水平与最危险方案中各影响因素的水平可知,2种方案中只有地层类型和隧道埋深的影响因素水平不同,其余影响因素的水平均相同。结合极差和方差分析中各影响因素的大小可知,隧道埋深与地层类型为次要因素,对试验的结果影响较小,从这2方面可以判断出此次正交试验结果具有一定的合理性和正确性。
5.2 以地表最大沉降值为评价指标
以常见的地表最大沉降量为评价指标,分析盾构隧道施工对地表沉降的影响,其正交试验结果见表5,地表最大沉降值极差分析结果如表8所示。由表8对正交试验结果的极差分析可知,盾构隧道下穿砌体建筑物过程中,以地表最大沉降量为评价指标时,地层类型的极差最大,建筑物长度的极差最小;按各因素极差从大到小得出影响因素的主次顺序为:地层类型、隧道轴线与建筑物中心线夹角、建筑物中心线与隧道轴线间距、隧道埋深、建筑物长度。
对以地表最大沉降值为指标的试验结果进行方差分析,精确估计各因素对试验结果影响的重要程度,方差分析结果如表9所示。根据表9中方差分析和试验因素显著性分析结果可知,地层类型的方差F值大于 F0.01,表明该因素对试验结果有高度显著的影响,为关键因素;而隧道埋深、隧道轴线与建筑物中心线间距、建筑物与隧道夹角、建筑物长度这4 个因素的方差F 值均小于F0.1,表明这4类因素水平的变化对地表最大沉降的影响较小,为次要因素,该结论与表8中极差分析结果一致。
对比4.1节和5.2节中的影响因素主次顺序可知,在正交试验中,采用不同评价指标得出的各影响因素的影响程度是不同的。对于本文而言,采用盾构隧道施工过程中砌体结构房屋墙体的最大拉应力增量为评价指标时,建筑物中心线与隧道轴线间距为最主要影响因素;而采用地表沉降作为评价指标时,高度显著的影响因素则是地层类型。
6 结论
(1)以不同的指标评价盾构隧道施工对周围砌体结构建筑物的影响时,得出的主要影响因素不同。以墙体最大拉应力增量为评价指标时,建筑物中心线与隧道轴线间距为主要影响因素;而以地表最大沉降值为评价指标时,地层类型为主要影响因素。
(2)当以建筑物墙体拉应力增量作为评价指标时,盾构隧道下穿砌体结构房屋的主次影响因素依次为,建筑物中心线与隧道轴线间距、建筑物长度、隧道轴线与建筑物中心线夹角、隧道埋深、地层类型。
(3)在隧道设计阶段,若不可避免地要下穿砌体结构建筑物时,应尽量避免建筑物中心线与隧道轴线的间距为1D,因为此间距为最危险间距。
参考文献
[1]朱才辉. 西安黄土层地铁盾构施工引起地层变形规律研究[D]. 陕西西安:西安理工大学,2009.
[2]丁祖德,彭立敏,施成华. 地铁隧道穿越角度对地表建筑物的影响分析[J]. 岩土力学,2011,32(11):3387-3392.
[3]张立茂,冉连月,吴贤国,等. 盾构施工临近建筑物变形影响因素关联性分析[J]. 铁道标准设计,2016,60(9): 94-99.
[4]王俊,林国进,唐协,等. 砂土地层盾构隧道稳定性三维离散元研究[J]. 西南交通大学学报,2018,53(2):312-321.
[5]魏纲,陈春来. 双圆盾构施工对邻近砌体建筑物影响的数值模拟[J]. 工业建筑,2012,42(1):117-122.
[6]赵淑芹. 盾构隧道施工对地面砌体结构房屋的影响[D]. 黑龙江哈尔滨:哈尔滨工业大学,2012.
[7]孙宇坤. 受盾构隧道施工影响的砌体结构房屋性状研究[D]. 浙江杭州:浙江大学,2012.
[8]化建新,郑建国.工程地质手册[M]. 北京:中国建筑工业出版社,2018.
[9]曹海静. 成都地铁砂卵石基坑变形监控指标研究[D].北京:中国铁道科学研究院,2015.
[10] 刘钊,李子春,刘国楠,等. 花岗岩残积土的修正摩尔库伦模型参数取值研究[J]. 铁道建筑,2017(3):89-92.
[11] 来弘鹏,郑海伟,何秋敏,等. 砂土地层盾构隧道小角度斜下穿既有隧道施工参数优化研究[J]. 中国公路学报,2018,31(10):130-140.
[12] 魏纲.双线盾构隧道施工环境效应评价与控制[M]. 北京:北京建筑工业出版社,2018.
[13] 李云雁,胡传荣.试验设计与数据处理[M]. 北京:化学工业出版社,2017.
[14] 白中坤,杨朝帅,于少辉. 正交试验法在旋喷桩参数试验中的应用[J]. 地下空间与工程学报,2014,10(3):624- 629.
[15] 王輝,王鹏,梁明纯. 地铁隧道开挖超前小导管预注浆参数对地表沉降的影响[J]. 铁道建筑,2019,59(3):47-51.
[16] 张雪婵. 软土地基狭长型深基坑性状分析[D]. 浙江杭州:浙江大学,2012.
[17] 焦建伟,王空前. 浅覆土盾构最小埋深的正交试验分析[J]. 现代隧道技术,2014,51(3):138-143,151.
[18] 周顺华. 地铁盾构法隧道下穿工程[M]. 北京:科学出版社,2017.
[19] 魏新江,魏纲,丁智. 盾构施工与邻近不同位置建筑物相互影响分析[J]. 岩土力学,2007,28(S1):505-510.
[20] 彭立敏,丁祖德,黄娟,等. 隧道穿越方式对地表建筑物变形影响的数值分析[J]. 中南大学学报(自然科学版),2012,43(1):308-314.
收稿日期 2020-03-21
责任编辑 朱开明

