基于经验模态分解的两种混合氨基酸太赫兹光谱分析研究

刘 婧，刘海顺，左 剑，张存林,，赵跃进，梁美彦

1. 北京理工大学，北京 1000812. 首都师范大学，北京 1000483. 山西大学，山西 太原 030013

引 言

氨基酸是构建生物细胞和组织的基本成分。L-苯丙氨酸和L-酪氨酸在合成神经递质和激素的过程中起重要作用，这些神经递质和激素参与了人体的糖和脂肪的代谢过程。这两种氨基酸具有相似的分子结构，不同在于L-酪氨酸多了一个羟基，这却导致了两种氨基酸在功能上具有明显区别。前人的研究表明，这两种氨基酸在低频振动上存在显著差异。近年来，太赫兹(THz)光谱学技术作为研究生物分子低频动力学的有效手段被广泛应用[1-2]，因此通过太赫兹光谱对氨基酸进行研究，对进一步了解蛋白质和相关生物活性具有重要意义。2005年和2010年，Yamamoto等[3-4]利用太赫兹手段对氨基酸及其多肽的低频谱进行了研究。2013年，Yu等[5]在太赫兹波段通过主成分分析(PCA)手段处理与吸收线形函数(ALF)方法，对两种氨基酸混合物进行了识别研究。

多变量校准方法[如偏最小二乘法(partial least squares，PLS)]已成功应用于太赫兹多组分光谱数据定量分析研究中。陈涛等[6]将太赫兹光谱技术与PLS回归手段结合，研究多组分药物混合物的实际浓度与预测浓度之间的一致性。Lu等[7]通过PLS和基于太赫兹吸收光谱的区间偏最小二乘(iPLS)回归对L-谷氨酸和L-谷氨酰胺的二元混合物进行了定性和定量的分析研究。

然而，传统校准技术由于仅在光谱和目标之间建立单个模型预测未知样品，其预测性能有时仍不尽人意。因此，具有更好精度的集成建模方法(ensemble modeling method)应运而生[8]。集成建模的基本概念是组合多个单独模型的优势以产生更好的预测结果。

1998年，Huang[9]提出了经验模态分解(empirical mode decomposition，EMD)的方法。该方法可以将信号自适应地分解为一组本征模式函数(intrinsic mode functions，IMF)，成功地广泛应用于信号和光谱处理中[10-11]。基于EMD方法的信号分析也已在太赫兹波段开始使用[12-15]。然而，在对物质进行定量分析的过程中，目前还没有报道基于EMD方法的太赫兹光谱PLS回归的相关工作。本文提出了一种基于EMD的PLS方法，用于定量分析研究不同浓度氨基酸混合物的太赫兹吸收光谱。该方法提取了基于前几个IMF的吸收光谱，用于建立PLS回归模型，比较了其结果与原始吸收谱的PLS建模结果。

1 实验部分

1.1 数据处理

EMD的主要思想是将信号f(t)分解为一系列本征模式函数(IMFs)。每个IMF应满足两个基本标准： (1)极值和零交叉数量必须相等或在整个数据集中最多有一个差异; (2)由局部最小值和最大值定义的包络，其平均值应为零[9]。该信号可写为

(1)

其中xk(t)是第k个IMF分量，rN(t)是残差函数。

信号f(t)的分解过程可归纳如下：

(1)找出f(t)的所有极值(最大值或最小值);

(2)使用三次样条曲线将所有局部最大值或最小值连接为上限或下限;

(3)计算包络m1(t)的平均值;

(4)提取新的数据序列h1(t)=f(t)-m1(t);

(5)迭代h1(t)，直到h1(t)满足IMF的上述两个标准，以此来找到第一个IMF分量x1(t);

(6)对信号r1(t)=f(t)-x1(t)重复上述步骤，并获取其余的IMF。

当残差函数rN(t)变为单调函数或常数时，该过程即可停止。由此可见，信号f(t)可以分解为一组IMF和残差函数。这里，IMF由不同的振荡模式组成，并且更高阶的IMF对应于较低频率的信息。

PLS是一种较为成熟的线性回归方法[6-7]。该模型的性能主要通过相关系数(R)，校正均方根误差(RMSEC)和预测均方根误差(RMSEP)这几个参数来评估。当一个模型具有更高R，更小的RMSEC和RMSEP时，该模型被认为是较理想的模型。

EMD-PLS方法的流程示意图如图1所示。原始的太赫兹时域信号首先通过EMD手段，分解为一系列IMF和一个残差函数，然后前几个IMF相加作为一个整体，随后对其吸收光谱进行重建。最后，建立PLS模型用于进一步的物质定量分析。

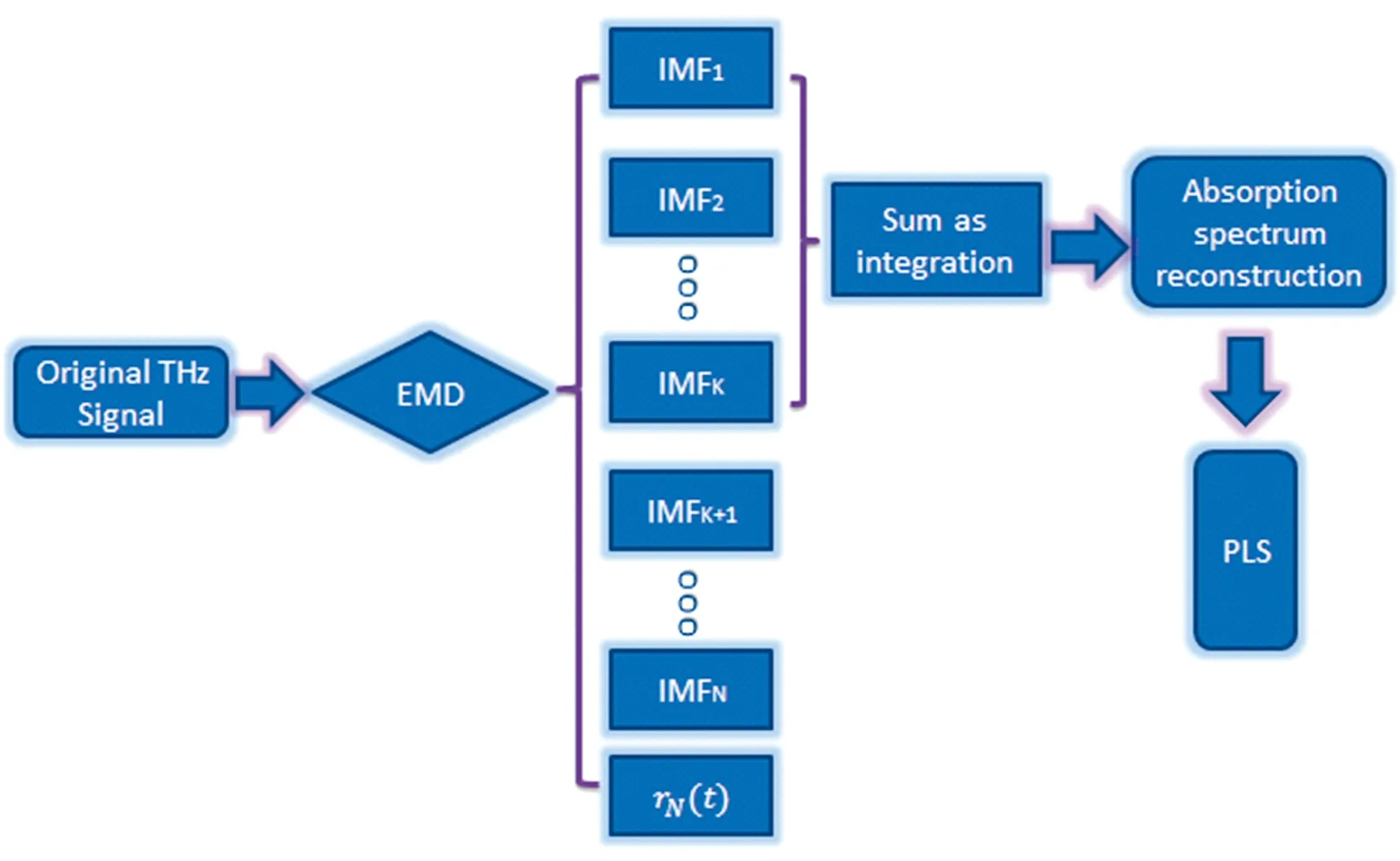
图1 EMD-PLS建模流程图Fig.1 Flowchart of EMD-PLS modeling

1.2 方法

氨基酸样品(L-苯丙氨酸和L-酪氨酸)与聚乙烯粉末充分混合(L-苯丙氨酸质量占比分别为0%，15%，25%，40%，50%，55%，60%，61%，64%，70%，75%，85%，95%，100%)，然后研磨成均匀的颗粒。并在5 t压力下被压成圆片。样品均购于sigma-aldrich公司。圆片样品的厚度约为0.6 mm，直径为13 mm。每个浓度的样品数量为2，共有28个圆片样品。使用太赫兹时域光谱(THz-TDS)系统对样品进行测试，样品被放置在两个抛物面镜的焦点之间。所有测量均在21 ℃下进行，相对湿度小于4%。

图2 (a) 28个氨基酸混合物样品的原始时域信号； (b) 28个氨基酸混合物样品的原始吸收信号Fig.2 (a) 28 original temporal signals and (b) absorptionspectra of 28 original amino acids samples

2 结果与讨论

图2(a)和(b)为28个原始THz时域信号及其在0.7～2.5 THz波段的吸收光谱。由图可知，该氨基酸混合物的三个吸收峰分别位于0.97，1.9和2.08 THz。可以看出，随着L-苯丙氨酸含量从100%降至0%，混合光谱吸收峰的幅值逐渐增加。所以，L-苯丙氨酸没有明显的特征峰，三个峰均来自于L-酪氨酸。前人的理论模拟结果表明，L-酪氨酸的吸收峰主要由分子的振动和扭转引起，即分子的不同振动模式和强度产生了不同的吸收峰[16]。

此处仅对L-苯丙氨酸浓度为0%样品的时域信号进行举例分析，以说明信号分解的过程，其余27个时域信号均按此方法进行处理。图3为该样品的分解结果，它可以分解为8个IMF和1个残差函数。很明显，一阶IMF(IMF1)信号具有最多的信号能量，而其余IMF信号能量随着阶数增加而减少。可以看出，低阶模式更接近原始时间信号。

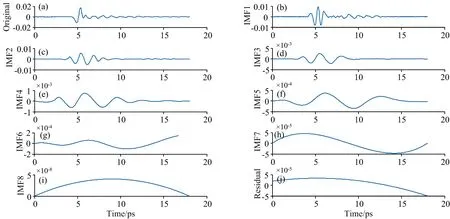
图3 L-苯丙氨酸浓度为0%样品EMD 分解后的IMF和残差函数Fig.3 EMD decomposed IMFs and residual function of concentration=0% sample

图4描述了L-苯丙氨酸浓度为 0%样品的时域信号经过EMD分解后，第一个IMF(IMF1)，前两个IMF叠加(IMF1+IMF2)，前三个IMF叠加(IMF1+IMF2+IMF3)，前四个IMF叠加(IMF1+IMF2+IMF3+IMF4)和前五个IMF叠加(IMF1+IMF2+IMF3+IMF4+IMF5)相应的吸收光谱。可以看出，由于低频信息不完整，IMF1的吸收光谱明显不同于其他吸收光谱。因此进一步建模中，我们不考虑IMF1。随后，使用PLS对剩余数据集与目标值之间建立了定量分析模型。此处，采用Kennard-Stone方法将数据集划分为校正和预测集。实验数据集中，18个样本作为校正集，并将剩余的10个样本作为预测集。这五组THz吸收光谱(原始与分解后)的PLS统计分析结果列于表1中。与原始结果相比，前两个IMF叠加的预测效果不好，说明前两个IMF叠加删除冗余信息的同时丢失了某些有用信息。虽然前五个IMF叠加在校正集中有较好结果，但是其RMSEP较大，说明其中可能存在噪声导致过度拟合。通过比较可以确定前四个IMF叠加具有最佳的预测效果，这证实了EMD方法的有效性。

表1 对两种氨基酸混合物的PLS校正与预测效果Table 1 PLS calibration and prediction performance statistics for binary mixtures

图4 L-苯丙氨酸浓度为 0%的样品EMD分解后，第一个IMF(IMF1)，前两个IMF叠加(IMF1+IMF2)，前三个IMF叠加(IMF1+IMF2+IMF3)，前四个IMF叠加(IMF1+IMF2+IMF3+IMF4))和前五个IMF叠加(IMF1+IMF2+IMF3+IMF4+IMF5)后相对应的吸收光谱

图5(a)和(b)分别为单独使用PLS模型和使用EMD-PLS模型(基于前四个IMF之和的结果)对不同氨基酸混合物样品实际浓度与预测浓度之间的相关性，可以看出EMD-PLS模型可以获得更理想的预测结果。

图5 (a)PLS模型和(b)EMD-PLS模型(IMF1+IMF2+IMF3+IMF4)下不同浓度氨基酸混合物样品的实际浓度与预测浓度的关系

3 结 论

提出了一种基于太赫兹光谱技术的多元校正模型(EMD-PLS)，对氨基酸混合物进行了定量分析。该方法首先通过EMD方法分解太赫兹时域信号，并将前几个IMF信号叠加替代原始信号，然后对原始信号和使用EMD处理信号对应的吸收谱进行PLS回归分析。定量分析结果表明，与其他吸收谱相比，基于前四个IMF叠加的吸收光谱具有更好的预测结果(Rp=0.996 1和RMSEP=0.019 8)，这说明EMD可以作为一种有效的预处理手段。该工作表明了基于EMD的太赫兹信号定量分析技术的有效性，证明了EMD-PLS模型可以实现较为理想的预测精度。