可验证的密文策略属性基加密安全外包方案*

闫玺玺, 何广辉, 于金霞

河南理工大学计算机科学与技术学院, 焦作454000

1 引言

随着云计算技术的出现与快速发展, 其强大的计算资源与存储性能越来越受到互联网各界领域的青睐, 也因此产生一种新的计算模式: 外包计算[1]. 它允许计算与存储资源匮乏的终端用户将一些耗时的计算外包给云服务器进行处理, 通过云计算按需付费这一特点, 用户便可享受到云端提供的各类信息服务.但由于云服务器并非是完全可信的, 数据持有者将要计算的任务上传给云端时, 同时也失去了对数据的实际控制, 如何保护数据中包含的私密信息, 是当前研究的安全问题之一. Sahai 与Waters 提出了一种新的公钥密码系统, 属性基加密(attribute-based encryption, ABE)[2], 数据拥有者通过访问策略可以有效地实现在云计算系统中数据的细粒度访问控制. 依照访问策略位置不同可以分为两类: 密文策略属性基加密(ciphertext-policy ABE, CP-ABE)[3]与密钥策略属性基加密(key-policy ABE, KP-ABE)[4]. 传统的属性基加密, 其计算代价会随着属性数量的增加和访问策略的复杂度呈线性递增的关系, 无疑给设备终端带来庞大的计算负担, 学者们也提出了各种属性基外包方案, 既能通过外包给云服务器来减少开销, 也能保护数据的隐私性. 例如在电子医疗系统中, 病人的健康纪录通常被外包在第三方机构, 病人的敏感信息得不到保障, 为了解决这种情况, Liu 等人设计了一种离线/在线的属性基签名方案[5], 通过引入离散对数的陷门哈希函数, 有效地实现了医疗文件的私密性, 签名者的匿名性与不可伪造性; 另外, 提出一种密文策略属性基签密方案[6], 签名的同时又满足加密, 可以有效地保障数据隐私的机密性与不可伪造性; 随后通过使用门限秘密共享与访问树结构, 提出了两种不同的RSS (redactable signature scheme)[7]方案来实现对医疗文件的完整性与对数据灵活的访问控制. 但因为用户私钥与属性相关, 存在多个用户的属性私钥相同的情况, Jiang 等人[8]提出了一种在雾计算中防止密钥委托滥用的密文策略属性基加密方案, 方案基于“与” 门访问结构与双线性群的性质进行构造, 同时对泄露的密钥具备可追踪功能; 针对属性撤销问题, Liu等人[9]提出了一种基于时间的直接撤销的CP-ABE 方案, 该方案通过将撤销列表嵌入到密文中, 撤销列表中的密钥都存在一个有效期, 同时对非撤销用户给出了一种密钥更新算法, 以此来实现更加灵活的访问控制功能.

由于在外包计算过程中, 云服务器可能因为“偷懒” 行为, 或受到敌手恶意攻击, 极大地影响计算结果的准确性, 因此如何设计一种有效的验证算法是数据外包过程中另一个安全挑战. 相关学者也将热点放在外包计算过程中如何由云服务器执行复杂的计算操作以及如何对返回计算的结果进行验证. Green 等人[10]首次在随机预言机模型下所提出的属性基加密外包方案, 该方案将解密操作交由解密服务器执行,通过将密文部分解密成ElGamal 类型的转换密文, 再交付给用户来降低用户计算代价. 王皓等人[11]给出属性基加密外包的形式化定义, 并给出了一个详细的CP-ABE 方案, 并在标准模型下证明方案是自适应安全的, 但方案效率较低. Li 等人[12]给出一种离线/在线属性基加密方案, 该方案在加密期间将庞大的计算开销使用离线/在线技术实现, 同时引入“变色龙” 哈希函数来实现解密前的验证功能, 并证明方案是适应性选择密文攻击安全, 但解密涉及的双线性对运算对用户依然是较大的开销. Fan 等人[13]提出一种云-雾计算中可验证多授权机构的外包方案, 该方案将加密与解密外包给离终端用户较近的雾节点, 相对于远端的云数据中心, 雾节点可以以较低的时延来进行计算, 很适合对数据进行实时计算处理. Zhang 等人[14]首次提出了一种完全外包方案, 即将密钥生成、加密与解密操作全部由云端来进行处理, 但缺乏验证机制. 该方案在加密阶段通过租用多个加密服务器来完成计算, 最后将多个加密服务器计算的结果交付给用户从而生成完整密文, 即使恶意用户与加密服务器勾结, 也不能截取有效的密文, 解密操作也是类似,但前提条件是假设服务器之间不会互相勾结. Zhao 等人[15]在原来Zhang 等人[14]方案的基础上提出了可验证的完全外包方案, 除了支持可验证功能, 其计算代价不会随着属性数量增加或访问策略复杂度而显著提升.

在上述方案的外包计算过程中, 数据拥有者只需计算常数个指数运算, 而与属性数量呈线性相关的部分指数运算外包给加密服务商执行, 但其底数与指数包含的信息对加密服务商而言是透明的, 尤其指数部分中包含有访问结构的部分信息, 如在外包解密运算中为重构共享秘密s 的有效秘密份额λi等信息会泄露, 因此对访问结构中部分信息进行隐藏格外重要. 针对外包加密过程中涉及到的指数运算, Fu 等人[16]提出了针对幂指数安全外包计算, 通过逻辑分割的方式, 将数据分割成随机片的形式来达到隐私保护的目的. Li 等人[17]将幂指数安全外包算法应用到属性基加密的方案中, 在外包加密过程中的指数运算, 通过幂指数安全外包算法, 可以有效的对密文中提到的底数与对数实现信息隐藏, 从而避免加密服务商获取密文中的私密信息, 同时支持对计算结果的可验证性, 但是因为由服务器对多个随机片计算的结果不能进行有效的区分, 因此在验证时正确验证的概率只有1/2.

针对上述问题, 本文提出了一种支持可验证的幂指数运算安全外包算法的属性基加密, 该算法是在Li等人[17]提出的算法基础上, 借鉴Fu 等人[16]的算法思想, 对验证操作进行完善, 使正确验证概率提升为“1”. 通过在属性基外包方案中引入该算法, 可以有效地实现在外包加密操作中, 对部分密文组件(如Ci,Di的计算) 执行一种新的数学分割方式, 并用产生的随机盲化对进行处理, 生成随机片的形式, 之后交由云服务器计算, 即将数据分割成由加密服务商计算的随机片的形式, 以此来达到数据的隐私保护这一目的, 方案中同时也支持可验证的外包解密这一操作. 最后在随机预言机模型下, 证明本文方案是选择性抗重放选择密文攻击(replay chosen-ciphertext attacks, RCCA)[18]安全.

2 预备知识

2.1 双线性映射

定义G,GT是素数阶为p 的两个乘法循环群, g 为群G 的生成元, 双线性映射e : G×G →GT满足下列性质:

(1) 双线性: e(ga,gb)=e(g,g)ab,∀g ∈G,∀a,b ∈.

(2) 非退化性: e(g,g)／=1.

2.2 线性秘密共享(LSSS)

2.3 判定性q-BDHE 假设

判定性q-BDHE 问题定义如下:

在安全参数下选择一个素数阶p 的群G, 随机选取a,s,b1,··· ,bq∈Zp, 公开

算法通过输出z ∈{0,1} 进行猜测, 如果

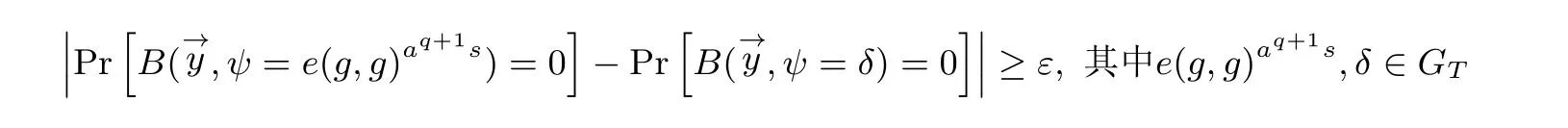
定义拥有ε 优势来解决判定性q-BDHE 问题, 若无多项式时间以不可忽略的优势解决q-BDHE 问题, 就称判定性q-BDHE 假设是成立的.

2.4 Rand 程序

在多数方案中, 用户借助子程序Rand[19]来生成随机盲化对, Rand 的输入是一个素数p 和一个底数g ∈RZ*p, 调用后输出一个具有(a,ga)mod p 形式的盲化对, 其中a ∈RZ*p, 实现这个子程序的方法常用的有两种: (1) 检查表方法; (2) 预处理[20]技术. 用户通过Rand 程序返回的随机数对对数据进行盲化处理, 进而发送给云服务器.

3 方案算法与安全模型定义

3.1 算法定义

本文所提的方案系统模型包括数据拥有者(data owner, DO), 加密服务商(encryption service provider, ESP), 存储服务商(storage service provider, SSP), 解密服务商(decryption service provider,DSP), 用户(data user, DU), 属性中心(attribute authority, AA)6 个实体组成.

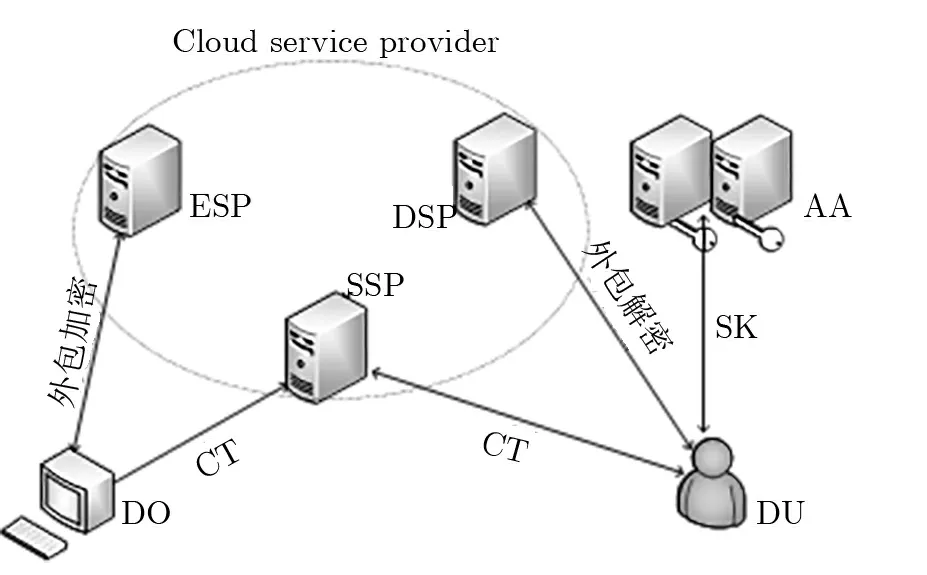
图1 安全外包属性基加密模型Figure 1 Secure outsourced attribute-based encryption model

数据拥有者DO 指定好访问策略, 先对数据执行简单指数运算的加密与异或操作, 然后将随属性数量线性增加的复杂的指数运算与模乘运算交由ESP, ESP 根据访问结构执行外包加密操作, DO 收到ESP返回的部分加密密文后对计算结果进行验证, 若验证成功则将DO 与ESP 计算的结果构成一个完整密文CT 上传到SSP.

终端用户DU 可以访问云服务器上密文文件并从SSP 下载密文, 由于终端设备资源有限, 将解密过程中涉及的指数与双线性对运算交由DSP 执行, DSP 利用AA 生成的转换密钥TK 来生成转换密文并发送给DU, DU 对DSP 返回的计算结果进行验证并用自己秘密保存的私钥SK 进行解密, 恢复出明文.

本文假设服务器之间不会发生共谋勾结, AA 是密钥分发机构, 是完全可信的, 方案所包含的算法由以下5 个算法组成.

Setup(λ,{0,1}*): 该算法输入安全参数λ 与系统属性集合{0,1}*, 输出系统公钥PK 与主私钥MSK.

Encrypt(PK,m ∈{0,1}λ,(M,ρ)): 加密算法由DO 与加密服务商ESP 合作共同完成, 通过输入PK, m 与访问策略, 在两种模幂安全外包算法Exp_1, Exp_2 下, ESP 执行部分加密操作生成中间密文CTout. 最后与DO 执行的加密操作生成完整密文CT.

KeyGenout(MSK,S): 密钥生成算法由AA 执行, 输入主私钥MSK 与用户属性集合S, 输出转换密钥TK 与私钥SK.

Transformout(TK,CT): 该算法由DSP 执行, 输入转换密钥TK 与完整密文CT, 输出转换密文CTtransform.

Decrypt(SK,CT′): 该算法由数据用户DU 执行, 输入转换密文CTtransform与用户私钥SK, 最后恢复出明文m.

3.2 安全模型

本文采用的安全游戏是选择性抗重放选择密文攻击(RCCA) 安全, 它允许对提供的密文进行修改却不会改变消息内容. 如果在Setup 阶段前加入Init 阶段, 则称是选择性安全.

Init. 敌手A 选择一个要挑战的访问策略(M*,ρ*), 发送给模拟者(挑战者)B.

Setup. 模拟者B 运行Setup 算法, 将PK 发送给敌手A.

Phase 1. 模拟者初始化一个空表T*, 一个集合D 与一个整数j =0, 敌手A 对属性集合S 重复进行以下询问.

· Creat(S): 模拟者设置j = j +1, 运行密钥生成算法KeyGen 来获得密钥对(SK,TK), 然后将(j,S,SK,TK) 存储在表T*中. 模拟者发送转换密钥TK 给敌手A.

· Corrupt(i): 如果在表T*中存在第i 个实体, 挑战者获得实体(i, S, SK, TK) 并设置D :=D ∪{S}, 将私钥SK 发送给敌手A, 如果不存在这个实体, 就返回终止符“⊥”.

· Decryt(i, CT): 如果在表T*中存在第i 个实体, 挑战者获得实体(i, S, SK, TK), 将解密算法中输入(SK,CT) 计算的输出结果返回给敌手A, 如果没有查询到第i 个实体, 就输出“⊥”.

Challenge. 敌手A 提交两个等长度消息m0,m1, 模拟者随机选择mβ,β ∈{0,1}, 运行Encrypt算法获得mβ的密文CT*, 最后模拟者将CT*发送给敌手A.

Phase 2. 与Phase 1 类似, 继续给出以上询问.

Guess. 敌手A 输出β′∈{0,1} 的值作为对β 的猜测, 如果β′= β, 我们称敌手A 赢得了该游戏,其敌手优势定义为:

定义1 若无多项式时间以不可忽略的优势来攻破上述安全模型, 那么我们就说本文提出的方案是选择性RCCA.

4 改进的模幂安全外包算法

一个安全外包[21]算法(T, U) 通常由两个实体组成, 可信的用户T 与不可信的云服务器U. 用户使用子程序Rand 产生的随机盲化对来实现对数据的分割隐藏, 将盲化后的随机数对上传到云服务器进行计算, 并将计算结果返回给用户, 最后用户进行验证. 针对幂指数运算外包算法, Li 等人[17]提出了多个底数模幂运算与单个底数模幂运算, 可有效的解决指数计算开销大的问题, 但是正确验证概率分别只有2/5与1/2. 为实现验证概率为“1”, 本文通过对Li 等人[17]算法进行完善, 提出了验证概率为“1” 的模幂安全外包算法.

4.1 多个底数模幂安全外包算法

应注意的是为提高逻辑分割过程中的安全性, x1,x2通常至少选取64 bit 长度.

(2) 用户T 向服务器U 询问计算的结果:

(3) 用户T 对服务器U 返回的结果用下面等式进行验证:

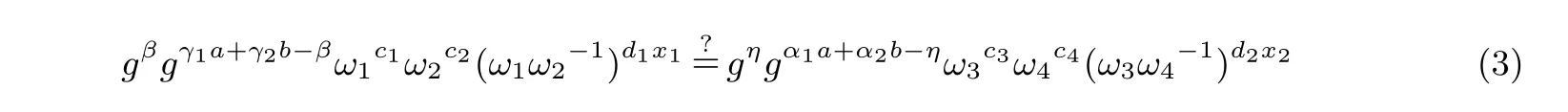
如果等式成立, 用户便可以计算出:

否则, 输出错误符号“⊥”.

4.2 单个底数模幂安全外包算法

算法描述: Exp2(a,u)→ua

给定一个素数阶p 的循环群G,群G 的生成元为g,任意选取一个底数u ∈RG 与一个指数a ∈R,输出结果uamod p.

(1) T 运行Rand 程序得到四组盲化随机数对(γ,gγ),(β,gβ), (α,gα),(η,gη) 同时对数据u,a 逻辑分割成由云服务器U 计算的随机片形式, 分割过程如下:

(3) 用户T 对服务器U 返回的结果用下面等式进行验证:

如果等式成立, 用户便可以计算出:

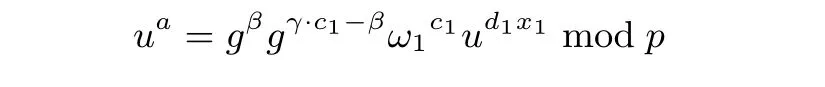
否则, 输出错误符号“⊥”.

5 方案构造

在云外包服务器模型下的安全外包密文策略属性基加密方案是基于Green 等人[10]的方案上来构造我们的方案, 具体由以下5 个算法组成, 每个算法的详细叙述如下:

Setup(λ,{0,1}*). 该算法输入一个安全参数λ 与系统属性集合, 然后选择一个素数阶p 的双线性群G, 群G 的生成元g, 一个将{0,1}*映射到群G 的哈希函数F. 另外, 随机选择的指数α,α ∈Zp, 选择两个哈希函数H1:{0,1}*→Zp与H2:{0,1}*→{0,1}λ最后输出系统主私钥MSK=(gα,PK), 系统公钥PK={g,e(g,g)α,ga,F,H1,H2}.

ESP 将每次的计算出的结果CTout发送给DO, 即

同样地, 依照Exp2算法来对Di进行计算, 过程与对Ci的计算类似.

(3) DO 对返回的计算结果进行验证, 验证公式如下:

若上述等式成立, 则说明ESP 准确地执行了计算结果, DO 根据返回的结果就可以输出完整密文CT=(C,C′,C′′,Ci,Di). 其中C,C′,C′′由DO 计算得出; Ci,Di由ESP 执行计算操作, 同时DO 还需对云服务器返回的计算结果进行验证.

最终输出部分解密密文CT′={C,C′′,CTtransform}.

Decrypt(SK,CT′). 该算法由用户执行, 通过输入CT′= {C,C′′,CTtransform} 与SK, 则计算r = C/(CTtransform)z,m=C ⊕H2(r), 并且计算s = H1(r,m). 如果C = r ·e(g,g)αs,CTtransform=e(g,g)sα/z, 则说明云服务器返回的计算结果正确, 便输出明文m.

6 安全性证明

本文所提出的两种幂指数安全外包算法以及所构造的方案, 我们分别从该算法可验证性与方案的安全性进行证明.

定理1 在单个不可信服务器模型下, 算法Exp1和Exp2是本文方案的一个正确性的实现, 那么正确验证概率为“1”.

证明: 对于Exp1, 数据拥有者对于输入的数据u1au2b, 那么可以准确地执行下列计算:

由式(7)与式(8)可知, 只要云服务器因懒惰或者遭受恶意攻击可返回错误结果, 那么当数据拥有者收到云服务器返回来的计算结果后, 通过验证公式(3)便可判断云服务器计算的结果是否正确, 若不符合等式, 说明云服务器计算产生错误, 因此数据拥有者便可以“1” 的概率检测出错误.

同理, Exp2证明过程与上述类似, 其正确验证概率为“1”.

定理2 假设判定性q-BDHE 假设在群G 与GT成立, 那么本文所提的方案在随机预言机模型下是选择性RCCA 安全.如果S 满足访问策略, 那么选一个“假” 转换密钥, 过程与上面类似, 选取一个随机值d ∈Zp, 运行KeyGen 算法来获得SK′, 设置TK = SK′, SK = (d,TK), 其中, d 如果被未知的值z = α/d,重新生成TK. 最后将(j,S,SK,TK) 存放在表T3中, 返回TK 给A.

· Corrupt(i): A 不能询问与访问策略(M*,ρ*) 相关联的密钥key. 如果在表T3中存在一个实体,那么B 就可以获得这个实体(i,S,SK,TK) 与D :=D ∪{S}, B 将SK 返回给A, 如果在表中不存在, 则输出“⊥”.

· Decrypt(i,CT): 我们假设所输入的密文已被部分解密, 由于B 和A 都可以访问TK 的值, 因此只有其中一个可以执行转换密文的操作. 与访问策略相关的密文CT=(C,C′′,CTtransform), 在表T3中可以查询到(i,S,SK,TK), 若查询不到或者S /∈(M,ρ), 输出“⊥” 给A. 如果第i 个实体中的密钥不满足挑战的访问策略(M*,ρ*), 执行以下过程:

所以, B 能以不可忽略的优势ε 攻破该判定性q-BDHE 困难问题假设.

7 性能分析

7.1 计算代价分析

将本文的方案与文献[10], 文献[17] 方案从功能方面与计算开销方面两个角度来进行分析比较, 在方案对比中, |ℓ| 代表策略属性集合数量大小, E 表示模指数运算, P 表示双线性对计算, M 表示群中模乘运算, 由于在方案里面开销较大的指数运算与双线性对运算, 以及较复杂的乘法运算, 因此忽略其它次要的运算(如哈希运算).

表1 主要从功能方面进行对比分析, 从中可以看到文献[10] 的方案仅仅将解密工作外包给云服务器进行计算, 加密工作还是由数据拥有者进行计算, 所以数据拥有者在加密期间涉及到繁重的指数运算以及较大的乘法运算. 文献[17] 与本文方案都是将加密操作和解密操作都外包给云服务器进行计算, 大大减少了用户终端的计算量. 文献[17] 不仅支持外包加密解密操作, 而且针对外包加密中的指数运算提出了两类幂指数安全外包算法, 通过数学分割以及盲化操作, 对密文组件中包含的底数与指数进行隐藏, 以此来实现数据的隐私保护, 然而多个底数模幂安全外包算法与单个底数模幂安全外包算法的正确性验证概率分别只有2/5、1/2. 本文方案将加密解密操作外包给云服务器执行, 并且通过对文献[17] 算法进行改进, 不仅可以实现隐私保护这一功能, 还将正确验证概率提升为“1”.

表1 功能分析Table 1 Function comparison

表2 主要从数据拥有者加密操作、验证以及数据使用者解密操作、验证等方面进行计算代价分析, 文献[17] 方案数据拥有者在加密阶段只涉及到2 次指数运算, 在对计算结果验证上需要2 次指数与1 次乘法, 数据用户在解密过程中进行1 次模乘操作, 但验证过程中涉及到5 次指数操作和1 次双线性对以及4 次模乘操作, 而双线性对计算代价远远大于模乘计算的代价. 文献[10] 中由于加密计算全部由数据拥有者操作, 所以加密阶段需要进行3|ℓ|+2 次指数运算和1|ℓ|+1 次模乘运算, 指数运算的工作量远远加重了数据拥有者的计算量. 本文方案在加密阶段进行2E 次操作, 与文献[10] 相同, 加密验证阶段我们比文献[17] 多进行了2 次指数运算和13 次乘法运算, 但是我们将验证的概率从2/5 提升到了“1”, 牺牲计算代价获得100% 的验证正确性是值得的. 解密阶段我们比文献[17] 多了1 次指数计算, 但我们的解密验证阶段仅需要1 次乘法与2 次指数运算, 比文献[17] 的1 次双线性运算, 5 次指数运算以及4 次乘法运算, 其计算代价要小很多.

整体来看, 我们的方案将数据加密和数据解密中的指数运算都进行了外包操作, 大大减少了用户终端的计算量, 而且本文方案中用户的加密验证和解密验证正确率达到了100%, 完全实现了外包计算的可靠性和安全性.

表2 计算代价分析Table 2 Comparison of computing overhead

7.2 实验分析

通过上述理论分析, 本文方案在功能与效率上更有优势, 为了更准确评估方案的实际性能, 通过实验进一步分析与文献[10]、文献[17] 在终端设备的计算量上的时间开销, 包括加解密时间与验证所需的时间.

实验环境: Windows 10 操作系统, Inter® Core(TM) i3-3217U(1.80 GHz)、内存2 GB, 实验代码基于JPBC-2.0.0 (java pairing-based cryptography library) 函数库与MyEclipse 开发环境进行编写, 其中模幂与模乘运算是分别调用库中G_1.powZn() 与G_1.mul() 两个函数进行测试.

实验设置: 在密文策略属性基加密方案中, 访问策略中属性个数影响加密与解密时间, 在实验过程中,由于庞大的计算开销外包给云服务器进行计算, 因此我们只测试用户端的计算时间. 我们在实验中设置属性个数为100, 每次递增10 个属性个数, 从而产生10 种不同的访问策略, 通过比较用户端在不同访问策略下的计算时间, 每个访问策略我们测试10 次, 取一个平均值作为实验结果.

图2 有两个子图, 图2(a) 与图2(b), 分别代表了数据拥有者的计算时间与数据用户的计算时间. 在图2(a) 中, 我们可以看到文献[10] 由于所有加密操作都由数据拥有者独立完成, 可以看到计算时间随着属性数量的增加线性递增, 文献[17] 与本文方案由于数据拥有者只承担部分加密操作, 可以看到时间不会随属性数量的增加而逐渐递增, 同时本文方案所需的计算时间要高于文献[17], 但我们将正确验证概率提升到“1”, 文献[17] 并不具备这项优势. 在图2(b) 中文献[17] 的用户解密与验证时间要高于本文方案与文献[10], 而本文方案与文献[10] 用户所花的计算时间几乎相同, 但因为文献[10] 中的加密运算时间随着属性数目增加而逐渐递增, 因此本文方案是更有效的.

综合分析, 本文方案中的数据拥有者与数据用户的计算时间不会随着访问策略中属性个数增加而递增, 虽然在加密过程中数据拥有者的计算时间成本略高, 但可以准确地验证云服务器返回的计算结果, 并且用户解密时间成本较低, 因此本文方案是可行的.

图2 仿真时间对比Figure 2 Comparison of simulation time

8 结语

为解决基于属性加密外包方案中的幂指数运算, 本文提出了一种针对幂指数运算的模幂安全外包算法, 通过对数据分割、盲化等操作, 在属性基加密方案中由ESP 执行的外包加密过程期间, 可以有效地对数据私密信息实现隐藏这一功能, 以及概率为“1” 的可验证性; 同时支持DSP 执行部分解密计算, 以此降低本地解密计算量, 用户通过哈希算法与异或操作进行外包解密结果的验证并恢复出明文. 最后在随机预言机模型下证明了方案的安全性, 并从功能与效率两方面进行比较, 表明我们的方案更具优势.