偏最小二乘近红外光谱模型中潜变量个数对模型传递性能的影响

李永琪，洪士军，黄 雯，张立国，葛 炯*，栾绍嵘，倪力军*

(1.华东理工大学 化学与分子工程学院,上海 200237;2.上海烟草集团有限责任公司 技术中心理化实验室，上海 200082)

近红外光谱(NIRs)技术作为一种快速、无损的绿色检测技术，在各行各业的定量与定性分析中得到了广泛应用[1]。该技术以一些具有代表性的定标样品的定量指标或定性指标为因变量，其近红外光谱信息为自变量，通过多元统计方法建立相关指标的近红外光谱定量模型或样品的定性模型，根据模型实现对未知样品的定量或定性分析[2]。建立一个良好的近红外光谱模型需要积累大量样品的光谱和待测性质数据，并优化模型中的相关参数，模型建立和维护的工作量较大。通常希望在一台机器上建立的光谱模型(该机器通常称为主机)能够转移到其他仪器上(简称为从机)继续使用[3]，简称为模型传递或模型共享[4-6]。但由于主、从机光谱在不同区域存在或大或小的差异，通常光谱模型传递到从机后误差会增大，因而出现了各种降低模型对从机样品预测误差的模型传递方法[7]。分段直接校正(Piecewise direct standardization，PDS)方法是最经典常用的模型传递方法，该方法以主、从机均测试的转移集样品为基础，通过对从机光谱分段校正后再应用主机模型预测从机样品[8]。

近红外光谱定量模型通常采用偏最小二乘(Partial least squares，PLS)方法建立样品光谱信息与待测物质信息间的数学模型[9]。PLS模型建立过程中需要确定潜变量的个数(nLVs)，一般采用留一交叉验证或四折(三折)交叉验证的方法确定nLVs[10]或是选取内部检验集样品预测误差最小时对应的潜变量个数作为最佳值。本课题组研究发现，采用这种原则确定的近红外光谱PLS模型通常能够对单台仪器给出不错的结果，但这样选取的nLVs往往个数偏多，会引入噪声和无效信息，导致模型传递时预测误差显著增大，使得模型不能在从机直接应用。本文以网上公开发布的玉米数据及烟草企业多台近红外仪器所测烟叶样品数据为例，探究nLVs的选取对主、从机模型误差的影响，为建立稳健、可共享的近红外光谱模型提供依据和支持。

1 实验与方法

1.1 样品与数据集

玉米样品数据集来自http://www.eigenvector.com/data/Corn/corn.mat。包含M5、MP5、MP6 3台近红外仪上测得的80 个玉米样品的近红外光谱及这些样品中主要营养成分的含量数据。玉米样品中水分的质量分数在9.38%～10.99%之间，均值为10.23%；蛋白质的质量分数在7.65%～9.71%之间，均值为8.67%;脂肪的质量分数在3.09%～3.83%之间，均值为3.50%；淀粉的质量分数在62.84%～66.47%之间，均值为64.69%。烟叶样品有2套数据集，Set A由 78个烟叶样本分别在主机M(Master)、4台从机S1、S2、S3和S4上测得的近红外光谱组成，5台近红外仪均为AntarisⅡ近红外仪器(赛默飞世尔科技有限公司)，生产年份不尽相同；Set B则由1 070个在主机M上测得的烟叶样本光谱组成。Set A、Set B中各烟叶样品的总植物碱采用YC/T 160-2002[11]测定，其含量在0.55%～6.30%之间。

1.2 模型建立与评价

根据课题组前期研究结果，采用标准正态变换(SNV)结合一阶导数进行31点平滑对样品的近红外光谱进行预处理可消除因散射和背景漂移引起的光谱误差，基于该预处理光谱所建模型与其他预处理光谱(多元散射校正、一阶导数、原始光谱等)模型的效果相当[12-13]。由于该法不需要使用其他样品的光谱信息，故本文采用SNV+一阶导数光谱建立玉米中主要营养成分及烟叶总植物碱的近红外光谱定量模型。采用蒙特卡洛采样(Monte-Carlo Sampling，MCS)方法剔除异常点[14]。采用综合考虑光谱与待测性质信息来筛选代表性样品的SPXY(Sample set partitioning based on jointx-ydistance)方法[15]挑选主机建模样本，剩余样品作为内部验证集。一般情况下采用建模集均方根残差(RMSEC)来评价模型的拟合性能，验证集的均方根残差(RMSEP)来评价模型的预测性能[2]。考虑到RMSEP相当于绝对误差，难以根据该指标判断模型误差的相对大小，本文增加检验集或从机样本模型预测值与实测值相对误差的绝对值均值(简称为平均相对误差，MRE)来评估模型对主、从机样本的预测性能。另外，为与国标[16-18]要求的评估指标相对应，本文还采用验证样品组分的近红外模型值扣除系统偏差后与其标准值(实测值)之间的校准标准差(SEP)来评估主机模型调整后的准确度。相关评价指标的计算公式如下：

(1)

(2)

(3)

(4)

式(1)～(4)中yi,actual为第i个样品的实测值，yi,predicted为第i个样品的模型预测值，m为检验集样品数目。biasm是系统偏差，即检验集样品i的近红外测定值与标准值(实测值)之差的均值。如果不考虑系统偏差校正，式(3)的SEP即为式(1)的RMSEP。

PLS回归分析时前n个潜变量(主因子)的方差之和占所有潜变量方差之和的百分比η称为累积贡献率，其计算公式如下：

(5)

式(5)中λi为第i个潜变量的方差，p为所有方差不为零的潜变量个数，p≤min{样本数,波长个数}。

对于从机，采用RMSEP、MRE评价模型转移后的准确度，采用重现性指标SR评价从机近红外测定结果与主机近红外测定结果的一致性。国标[16]定义玉米水分、蛋白质近红外模型测定结果再现性指标SR的计算公式如下：

(6)

(7)

式(6)与(7)中的yi,slave与yi,master分别表示样品i的从机近红外测定值和主机近红外测定值；biast为验证样品i的从机近红外测定值与主机近红外测定值之差的均值，m为检验集(预测集)样本个数。

对于玉米中的脂肪与淀粉，国标要求在不同实验室，由不同操作人员使用同一型号不同设备，按相同测试方法，对相同的玉米样品的两个脂肪独立实验结果之间的绝对差值应不大于0.3%[17]，对相同的玉米样品的两个淀粉独立实验结果之间差值应不大于其算术平均值的15%[18]。参照国标的上述描述，本文定义玉米中脂肪、淀粉的再现性评价指标SRo与SRs如下：

(8)

(9)

式(9)中的yi,m为样品i的主机近红外测定值yi,master与从机近红外测定值yi,slave的均值。表1列出了国标规定的玉米中4种主要成分近红外模型相关评价指标的范围(上限)。

本文所有算法在MATLAB平台完成。

表1 粮油近红外分析仪性能基本要求中玉米主要成分的近红外模型评价标准[16-18]Table 1 Near infrared model evaluation standards for the main components of corn based on the basic performance requirements of near infrared analyzers for determining grain and oil contents[16-18]

2 结果与讨论

2.1 玉米中主要成分的PLS-NIRs模型对主机样品的预测误差随nLVs的变化

3台仪器上测定的玉米样品的平均光谱如图1所示，由该图可看出M5与MP5、MP6的原始平均光谱有明显差异，经SNV+一阶导数预处理后3台仪器上样品的平均光谱差异减小，但在某些波峰、波谷区域仍有肉眼可见的差异，MP6与MP5的平均光谱很相近。故选取M5作为主机，MP5、MP6两台光谱仪为从机。MCS方法未发现异常样本。根据SPXY方法从M5测试的80个玉米样品中选取前60个样品作为校正集，剩余20个样品作为内部检验集。

图2 玉米中4种成分含量的PLS-NIRs模型对主机检验 集样品的平均相对误差(MRE)随nLVs的变化Fig.2 The average relative error(MRE) of the PLS-NIRs model for the content of the four components in corn of the samples of the host test set varies with nLVs

图2为主机M5检验集样品各主要成分的平均相对误差随nLVs的变化。由该图可知，nLVs=1时，各成分的MRE已经小于3%，淀粉的MRE在nLVs=1时甚至低于1%。蛋白质、水分、脂肪含量的MRE均呈现在nLVs<10范围逐步降低到一个相对低点后有所升高，nLVs>10后又逐步降低的趋势。一般选取预测误差第一次达到相对最小时对应的nLVs作为最佳潜变量个数。根据该原则，脂肪和淀粉模型可选nLVs = 6；蛋白质和水分模型可选nLVs = 4。

采用留一交叉验证、四折交叉验证确定的玉米各营养成分的PLS模型中nLVs一般在5～10之间。以水分含量的PLS-NIRs模型为例，模型的前5个潜变量(LV)对应的方差分别为：0.999 39、0.000 44、0.000 08、0.000 05、0.000 01。第一个潜变量的方差非常之大，占据了所有潜变量方差之和的99.9%以上。玉米中另外3个成分脂肪、蛋白质及淀粉含量PLS-NIRs模型的第一个潜变量对应的累积贡献率也大于99.9%。因此，如果根据前nLVs个潜变量累积贡献率大于99.9%选取潜变量个数，玉米样品近红外光谱模型的nLVs=1，该值大大小于常规方法确定的潜变量个数。

2.2 潜变量个数对玉米中主要成分PLS-NIRs模型及模型转移结果的影响

表2～4给出了不同潜变量个数下所建立的主机模型对主机样品和从机样品中水分、脂肪和淀粉含量的预测结果，以及经过PDS校正后模型对从机样品的预测结果。根据文献建议值及经验，本文选择PDS校正方法中转移因子数为2，转移集数目为12个，窗口宽度为5，容忍度为0.01[19]。

蛋白质预测结果与表1相似，限于篇幅，该结果省略。表2～4中斜体数据表明对应的指标满足表1的要求。由这3个表可知，不同潜变量个数所建模型中，nLVs=1时所建立的PLS-NIRs模型直接转移到从机后，对从机样品各成分含量的预测误差RMSEP及MRE最小，且模型预测从机样品的误差与主机样品预测误差相差不多。模型对主机验证集样品的SEP以及从机的再现性评价指标均满足表1所列的国标要求。PDS校正对nLVs=1下所建模型的传递效果的改进很有限，且PDS校正后模型对从机样品脂肪、淀粉含量的预测误差高于模型直接传递的预测误差(见表3、表4中*标注的数据)。说明模型直接传递误差不大时，没必要采用PDS方法进行模型传递。

由留一交叉验证和四折交叉验证选取的nLVs均大于4，在此原则下建立的玉米各营养成分PLS-NIRs模型对主机样品的预测误差RMSEP、MRE随nLVs的增大而不同程度地降低，但各模型对从机样品的RMSEP及MRE显著增大，是主机样品对应误差指标的几倍到十几倍，其误差水平超出许可范围。经PDS校正从机光谱后，模型对从机样品的预测误差降低到与主机相当的水平。nLVs>1时建立的玉米营养成分的PLS-NIRs模型给出的主、从机预测值的重现性较nLVs=1时所建模型的重现性高一个量级，nLVs>4时所建模型对从机样品中各成分含量的预测值大多不满足表1所列的重现性指标要求。说明从第二个潜变量开始，仪器间光谱信息的一致性变差，导致nLVs>1时各模型主、从机间近红外测试值的重现性变差。虽然nLVs增大可改进模型对主机样品的预测准确度，但会导致模型传递误差变大，使得模型无法直接转移到从机。

表2 玉米水分PLS-NIRs模型直接传递及PDS校正后的传递结果Table 2 Direct transfer results and transfer results after PDS correction of the PLS-NIRs model for predicting moisture content in corn

表3 玉米脂肪PLS-NIRs模型直接传递及PDS校正后的传递结果Table 3 Direct transfer results and transfer results after PDS correction of the PLS-NIRs model for predicting oil content in corn

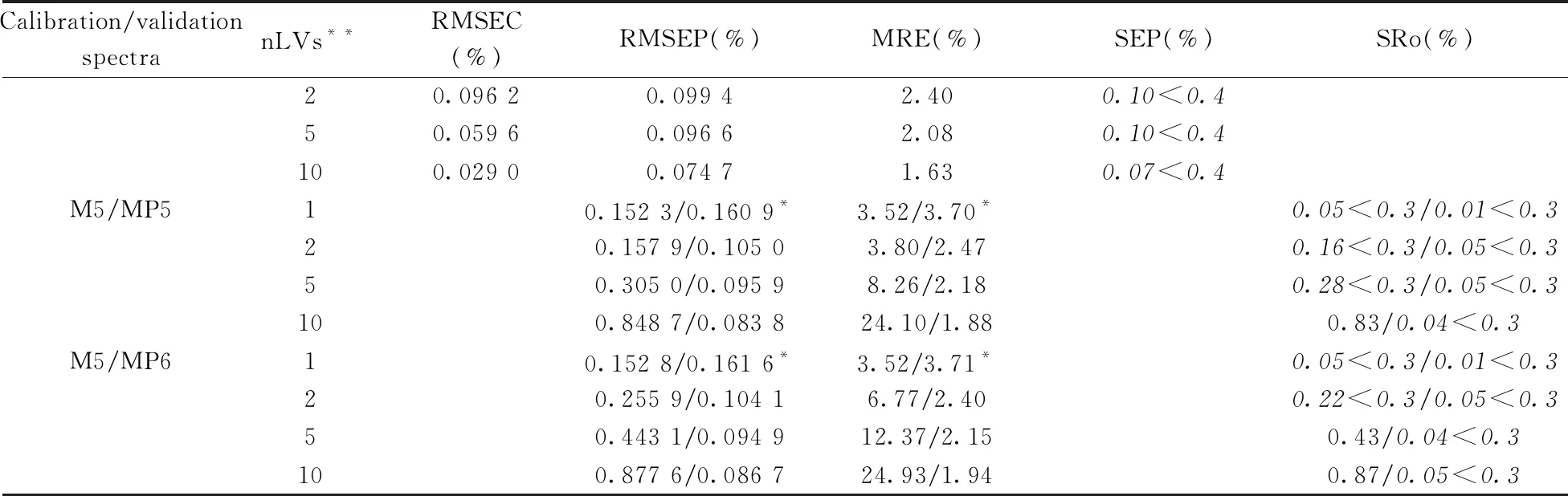
(续表3)

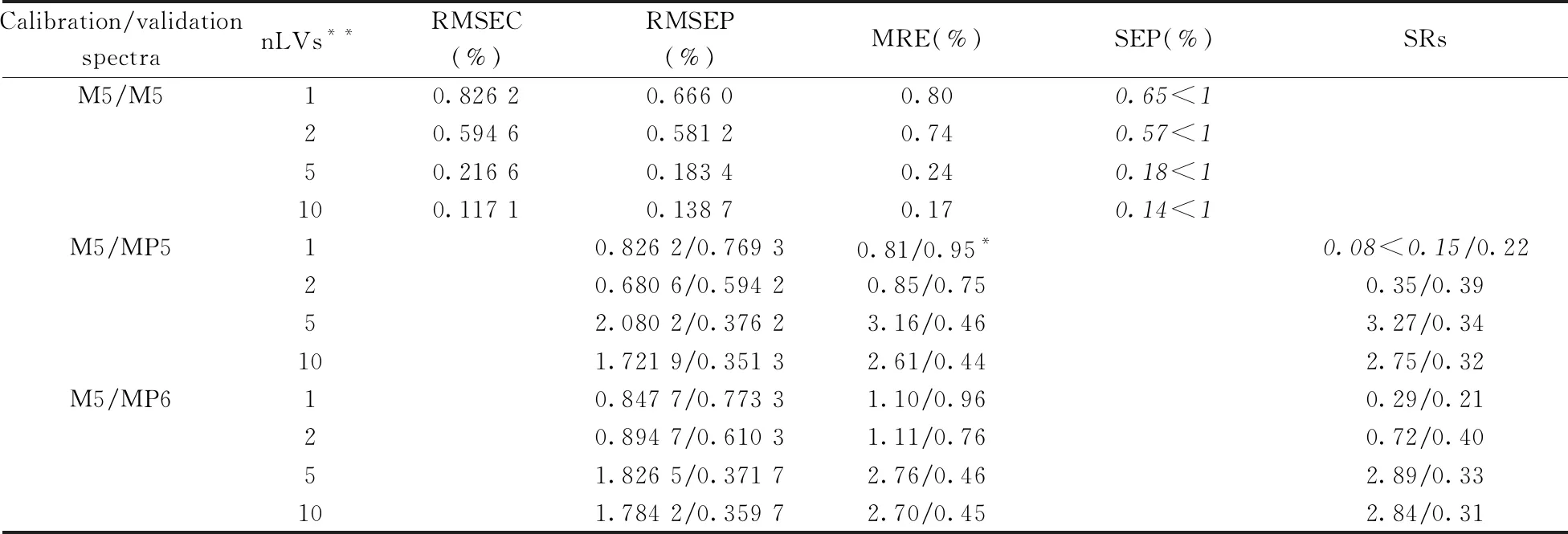
表4 玉米淀粉PLS-NIRs模型直接传递及PDS校正后的模型传递结果Table 4 Direct transfer results and transfer results after PDS correction of the PLS-NIRs model for predicting starch content in corn

2.3 潜变量个数对烟叶总植物碱PLS-NIRs模型及模型转移结果的影响

以烟叶数据集中Set B作为建模集，Set A中主机的78个样品光谱为外部验证集，建立烟叶总植物碱的PLS-NIRs模型。通过MCS方法发现两个异常点，最终取Set B中的1 068个样本建立模型。根据累积贡献率大于99.9%选取的nLVs=13，四折和留一交叉验证选取的nLVs分别为16和19。表5给出了分别取13、16、19个潜变量时得到的烟叶总植物碱的PLS-NIRs模型结果，以及经过PDS校正后模型对从机样品的预测结果。表中斜体数据表明对应的指标满足小于6%的企业内控要求。取nLVs=13所建立的烟叶总植物碱PLS-NIRs模型直接转移到从机后，对S1从机的MRE小于6%，但对其他3台从机样品的MRE均大于6%；经PDS校正后，nLVs=13下所建模型对4台从机的预测误差均小于6%。而潜变量个数大于13时所建立的烟叶总植物碱的PLS-NIRs模型对主机样品的预测误改进很有限，且模型直接转移到从机后，除nLVs=16模型对S1样品的MRE小于6%外，对其他从机样品的MRE均大于6%，即使经过PDS校正也不能保证这些模型对所有从机样品的MRE满足企业的内控要求。

2.4 讨论与分析

玉米样品中主要成分的PLS-NIRs模型潜变量个数取1时，模型传递误差最小且4个成分的PLS-NIRs模型对主、从机样品预测值的重现性均满足国标要求。由于第一潜变量的方差已经占据所有潜变量方差总和的99.9%以上，说明第一潜变量之后的潜变量所包含的有效信息加起来不足0.1%，引入这些有效信息很少的潜变量，易导致模型过拟合：即对建模样品或主机样品模型的误差很小(小于潜变量个数为1的模型误差)，但对从机样品的误差过大。

表5 烟叶总植物碱PLS-NIRs模型直接传递及PDS校正后的传递结果Table 5 Direct transfer results and transfer results after PDS correction of the PLS-NIRs model for predicting total alkaloid contents in tobacco leaves

图3 玉米水分PLS-NIRs模型的第一载荷轴与M5、 MP5差谱绝对值的标准方差谱(SDDSI1)Fig.3 The first loading of PLS-NIRs model for predicting corn moisture and the standard deviance spectrum of absolute difference spectra between M5 and MP5

图3给出了玉米中水分PLS-NIRs模型的第一载荷轴及M5、MP5样品光谱的差谱绝对值的标准方差光谱(简称SDDSI1)。由图3可看出，第一载荷轴的峰值位于SDDSI1很小或较小的区域，而SDDSI1的峰值所对应第一载荷取值均在0附近，说明第一潜变量中对模型贡献大的波长点有效避开了仪器间光谱差异波动大的区域，因此当玉米PLS模型的潜变量个数nLVs取1时，对从机样品的预测误差与主机相当。其次，该模型摒弃了方差小于0.1%、有效信息含量很低的潜变量，大大提高了模型的稳健性，使得模型传递到从机后误差无明显变化。

3 结 论

PLS-NIRs模型中潜变量个数nLVs的选取对模型的稳健性、传递性能有重要影响。nLVs够用即可，过高的nLVs容易造成过拟合，影响模型的稳健性，使得模型转移时误差过大。根据累积贡献率大于99.9%选取nLVs建立的PLS-NIRs模型稳健性最好，易于获得好的模型传递结果。而根据留一交叉验证及四折交叉验证或单台(主机)仪器验证集预测误差最小等原则选取的nLVs个数均高于根据累积贡献率大于99.9%选取的nLVs，易导致模型过拟合。

建议根据累计贡献率大于99.9%或接近99.9%时对应的nLVs建立近红外光谱模型，虽然对于主机而言，模型误差比根据留一交叉验证或四折交叉验证选取nLVs建立的模型误差稍高，但模型传递误差小，易于实现模型共享，获得好的模型传递效果。本结论对玉米、烟叶之外的其他类型样品是否成立有待进一步验证。