不同压采方案对阜新地区地下水位变幅的影响评估
丰亚丽
(辽宁省盘锦水文局,辽宁 盘锦 124000)
0 引 言
阜新地区位于辽宁的西部,属于典型旱区,区域地表水资源量较贫乏,地下水是区域水资源供需补给的重要成分[1]。当前,在最严格的水资源管理制度下,对区域地下水开采控制力度不断增强,为保障阜新地区地下水资源的可持续利用,需要对区域地下水变化影响因素进行有效评估[2]。杨玉光[3]对阜新地区水资源承载能力进行了评估分析,结果表明区域地下水资源的承载能力有所减弱,尤其是从2015年以后,阜新地区由于河道来水量逐变少,使得区域地下水得不到有效补给,地下水埋深呈现递减变化[4]。由于地表水资源供给量较少,除了流域外调水措施,地下水补给是解决当前阜新地区水资源供需矛盾日益紧张的有效措施之一[5]。合理设置区域地下水压采方案将对区域地下水资源优化配置至关重要,为此需要结合模拟分析方法,实现不同地下水压采方案对区域地下水位的影响分析。李绍飞[6]结合地下水数值模型对不同地下水开采方案对天津地区地下水修复效果进行了评估,评估结果为天津地下水资源优化配置提供了重要参考。许多学者的研究表明[7-12],Richards模型可综合考虑区域水文地质参数,模拟的地下水位变幅和区域实际水位变化吻合度均较高,但该模型在辽宁地区还未进行相关应用,为此结合Richards地下水模拟模型,以阜新地区为研究案例,对该区域不同地下水压采方案下的水位变幅进行模拟,从而实现不同压采方案对地下水位变幅的影响评估,研究成果将为阜新乃至辽宁其他区域地下水资源规划和可持续利用提供方法参考。
1 评估方法
文章采用Richards地下水模拟模型,通过不同地下水压采方案,调整该模型的计算参数,实现不同地下水压采方案下的水位计算值,和未开采前的水位进行对比,分析其水位的动态变幅,从而分析该变幅是否对区域地下水承载能力产生影响。Richards模型首选对各控制计算节点的水量进行分析:
(1)
式中:△Hi表示为控制节点水量,m3;Bβ和Aβ表示不同计算单位的计算面积,m2以及地下水埋深,m;△Hi为计算节点的水位,m;Ss为计算节点的补给率,%。在进行数值模拟时首选需要确定地下水源汇项,即为计算节点的水量补给,其计算方程为:
(2)
式中:Qsi为地下水源汇补给流量,m3/s;Si为计算节点i的源汇补给率,%。 在此基础上对土壤垂向渗透流量进行分析:
(3)

(4)

(5)

(6)
式中:△β为不同节点控制单元的水力传导度均值;Hs为第s计算节点的水位,m;bi、bs、ci、cs表示为水力传导度计算系数。由于各控制单元流量方向不同,因此需要对控制单元进行均衡计算:
(7)
式中:Qsi和Qvi为均通过隐式方程进行求解。
2 实例应用
2.1 区域概况
以阜新地区为研究实例,为辽宁省水资源最为短缺的地区,区域属于典型的干旱气候,多年降水量平均值为492mm,蒸发量多年均值为1740.5mm。阜新地区丘陵地形占总面积比例约为68%,平原和山间河谷之间赋存大量的地下含水层,地下水单井出水量可在600-3000m3/d之间。河套冲击扇区域地下水富集程度较低,砂砾、砾石混凝土的岩性特征较为明显,地下水单井出水量<100m3/d。结合阜新地区河套冲击扇区域和山丘河谷两个地下水观测井作为模型数据,对地下水模型进行参数设置和验证分析。
2.2 模型参数设置
分别结合两个区域水文地质概况,对Richards地下水模拟模型潜水层和深水层的参数进行设置,参数设置情况见表1和表2。

表1 河套冲击扇区域参数设置结果

表2 山丘河谷区域参数设置结果
阜新地区冲击扇区域主要为砂、砾岩体,占总岩体比重为75%,其次为灰岩及其他小类地质岩。山丘河谷去主要为页岩和砂岩,占据的比重超过80%,碎屑岩占据的比重较小。采用抽水试验对模型需要的水力传导度、渗透水补给率、侧向和垂向渗透系数进行分析,从冲击扇区域参数分析结果可看出,参数设置较为合理,灰岩的水力传导度较大,这主要和其岩体特征有关,砂岩的渗透补给率系数较高,这主要和砂岩孔隙度较大,便于水量渗透有关。深水层的各项参数要高于浅水层,这主要是因为浅水层受土壤包气态的影响较大,使得其地下水流较为明显。从山丘河谷参数分析结果可看出,碎屑岩的水力传导度最大,砂岩的最低,碎屑岩由于孔隙率较大,使得其水力传导度一般较高。和河套冲击扇区域较为一致,受土壤包气带影响,深水层的各项参数要大于浅水层。
2.2 模型验证结果
在模型参数设置基础上,结合6组抽水试验对阜新河套冲击扇区域和山丘河谷区地下水模型的计算效率进行对比分析,结果见表3。
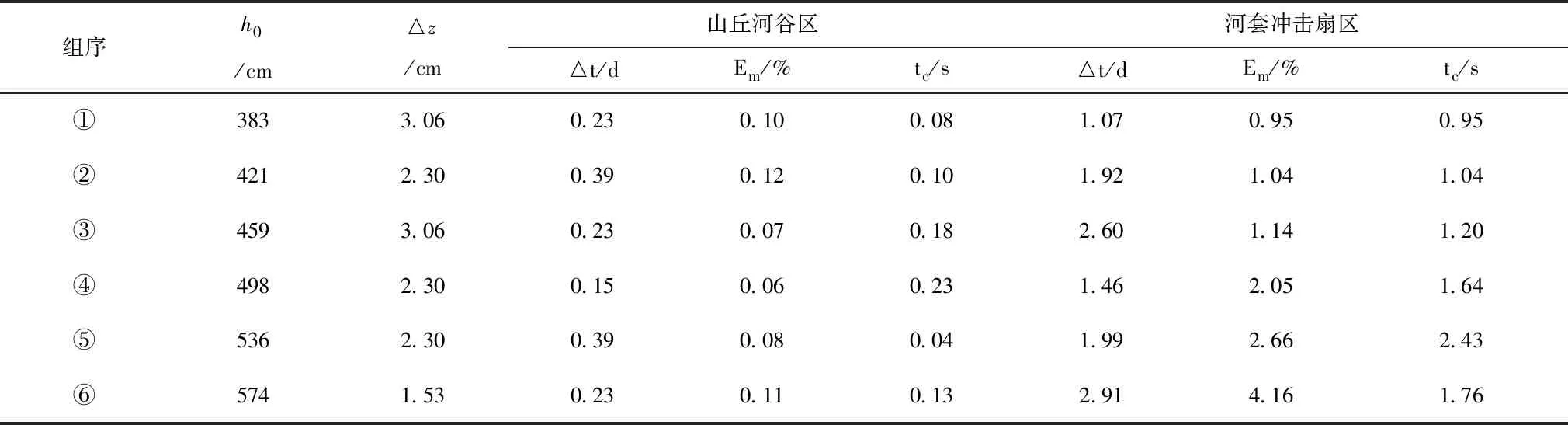
表3 不同区域地下水模拟效率验证结果
从各抽水试验的分析结果可看出,Richards地下水模拟模型在阜新地区地下水模拟具有一定的精度,基本可满足区域地下水位的预测分析。从对比恩熙结果可看出,山丘河谷区计算效率要好于河套冲击扇区,这主要是因为山丘河谷区地下水富集程度较高,地下水模拟模型受数据输入不确定性误差较小,而河套冲击扇区由于由于地下水富集程度较低,因此其模型输入的水位和参数数据不确定性程度要高于山丘河谷区,使得其计算效率系数和各控制节点单元的计算时间都要明显高于山丘河谷区,因此可表明,Richards地下水模拟模型在地下水富集较高的区域一般模拟精度要好于地下水资源富集度较低的区域。
2.3 不同开采方案下的潜水位动态变幅分析
在模型验证的基础上,通过设定阜新地区河套冲击扇及山丘河谷区域两种主要地下水开采方案(见表4和表5,)作为模型输入,主要调整模型的水力传导度和补给率两个参数,对不同地下水开采方案下的地下水位进行变幅的动态分析,水位变幅结果见表6和表7。
从河套冲击扇区域的两种地下水开采方案可看出,主要是对浅层地下水进行开采,地下水开采量每年在352万m3-505万m3,深层地下水开采量较小,主要考虑保护区域深层的地下水水量,其年均开采量<100万m3。从表6河套冲击扇区域的不同地下水开采方案的水位变幅可看出,由于河套冲击扇区域地下水富集程度较低,因此其不同试验组序下地下水动态变幅程度总体较低,不同地下水压采方案下浅层地下水变幅在-0.11--0.34m之间,且第二种开采方案下的水位变幅较大,这主要是因为第二种地下水压采率相比于第一种压采方案偏高,且压采时间较为集中,而第一种压采方案时间间隔较长,地下水补给率较好,因此对其地下水位变幅影响程度较低。在河套冲击扇区域一般建议压采时间间隔10-15d左右,山丘河谷区域压采时间间隔6-8左右,利于区域地下水的有效补给。从区域山丘河谷的水位变幅可看出,由于阜新地区山丘河谷地下水相比于冲击扇区较为充沛,使得其地下水压采率和压采量均要高于河套冲击扇区域,使得其不同地下水开采方案下的水位变幅明显增加,但由于山丘河谷地下水埋深一般较大,因此只要压采量符合区域地下水可承载的能力,其基本影响较低,从各试验组序下的水位变幅结果可看出,各开采方案下浅层地下水位变幅在-0.15--0.45m之间,深层地下水位变幅在-0.07--0.18m之间,且同样第二种压采方案下的水位变幅更大。从杨玉光[3]对阜新地区水资源承载能力的分析结果可知,设定两种地下水开采方案下的水位变幅均可满足阜新地区地下水资源承载能力需求。

表4 河套冲击扇区域地下水开采方案
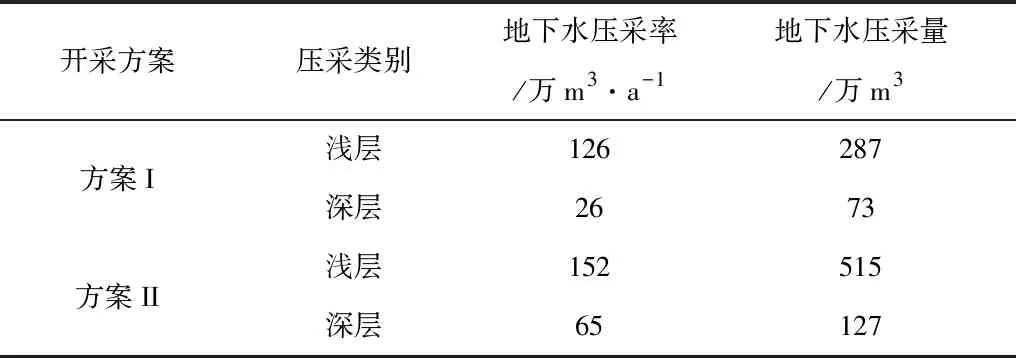
表5 山丘河谷区域不同地下水开采方案

表6 河套冲击扇区域不同地下水压采方案下的水位变幅评估结果
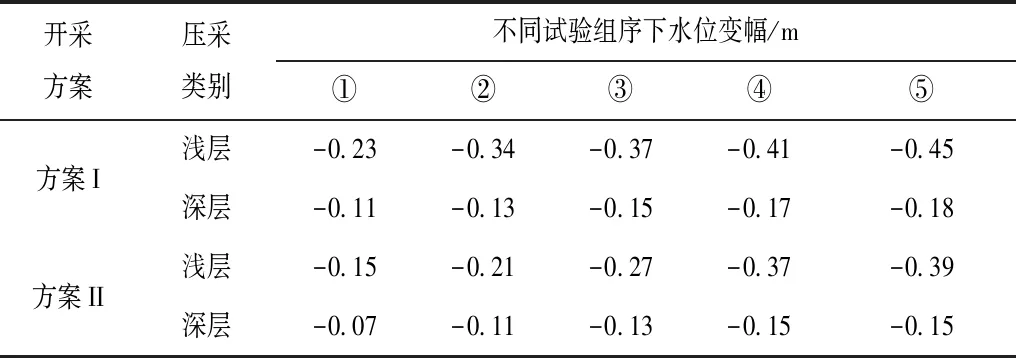
表7 山丘河谷区域不同地下水压采方案下的水位变幅评估结果
3 研究结论
1)在采用Richards地下水模拟模型进行区域地下水位变幅模拟时,需要结合区域不同水文地质分区来分别进行模型参数的设置,从而提高区域地下水位变幅模拟精度;
2)Richards地下水模拟模型在地下水富集较高的区域一般模拟精度要好于地下水资源富集度较低的区域,在具体模拟不同地下水开采方案对区域地下水位影响时,主要是调整水力传导度和渗透补给率两个参数;
3)在河套冲击扇区域一般建议压采时间间隔10-15d左右, 山丘河谷区域压采时间间隔6-8左右,利于区域地下水的有效补给;

