承中有升,合于无声
——基于“单元统整”背景下《梯形的认识》课后研讨
王 沛
(青岛市市南区基隆路小学 山东·青岛 266000)
今天探讨的主题是:“承中有升,合于无声”,是基于“单元统整”背景下《梯形的认识》一课的课后研讨。
1 本节课在教材中的位置
《图形的认识》这一单元,教材改变了过去将“角和三角形”、“图形的认识和面积”分开的编排方式,而是根据知识的逻辑联系整合安排教学内容,把三角形、平行四边形和梯形的认识集中学习。这样的新安排符合学生的认知特点,有助于学生建构知识体系。《梯形认识》这节课,是学生学习了三角形的认识、分类、三边关系、内角和,及平行四边形的认识之后学习的,是本单元认识多边形的最后一个新授内容。
应该说《教学参考》中给我们一个非常重要的信号:教师可以根据知识的逻辑顺序,整合安排教学内容。基于教材的编写意图,也基于本节课在本单元的地位。老师们前期在多次磨课中,确立了“承中有升”、“合于无声”的单元统整目标。承,即承上启下。合,就是找到内在联系,抓住本质,总结提升。
2 承中有升
无疑《梯形的认识》与《平行四边形的认识》有着密切的联系。
本节课教师在教学中,特别注意承接前一节课的两条线,一个是明线,即数学知识线;一个是暗线,即思想方法线。
2.1 知识线——认知结构线
在第一次备课中,教师设计了多次的动手操作环节,力图通过操作——学生剪一刀的这样一个推理过程认识梯形。在第二稿备课中,大家查阅了大量“单元统整”相关资料,老师们认识到:单元统整应当从已有的经验开始,经历学习过程增加新的经验,发展成为下一次学习的新经验。基于此,备课的二稿做了较大的修改,推翻了原来的设计思路,而更大的去承接平行四边形的一个认知结构:“由生活出发——抽象出图形——再研究它的特征及定义——再画高——生活应用”见图1)。
2.2 思想方法线
在本节课中,呈现了这样几条思想方法主线:(1)承接长方形、正方形和平行四边形,教师追问问:“同学们,你想从从哪些方面研究梯形?”学生回答:“边和角”。(2)在研究梯形特征时,教师引导学生回忆:“在研究平行四边形时,咱们都经历了怎样的研究过程?”猜想——验证——得出结论。
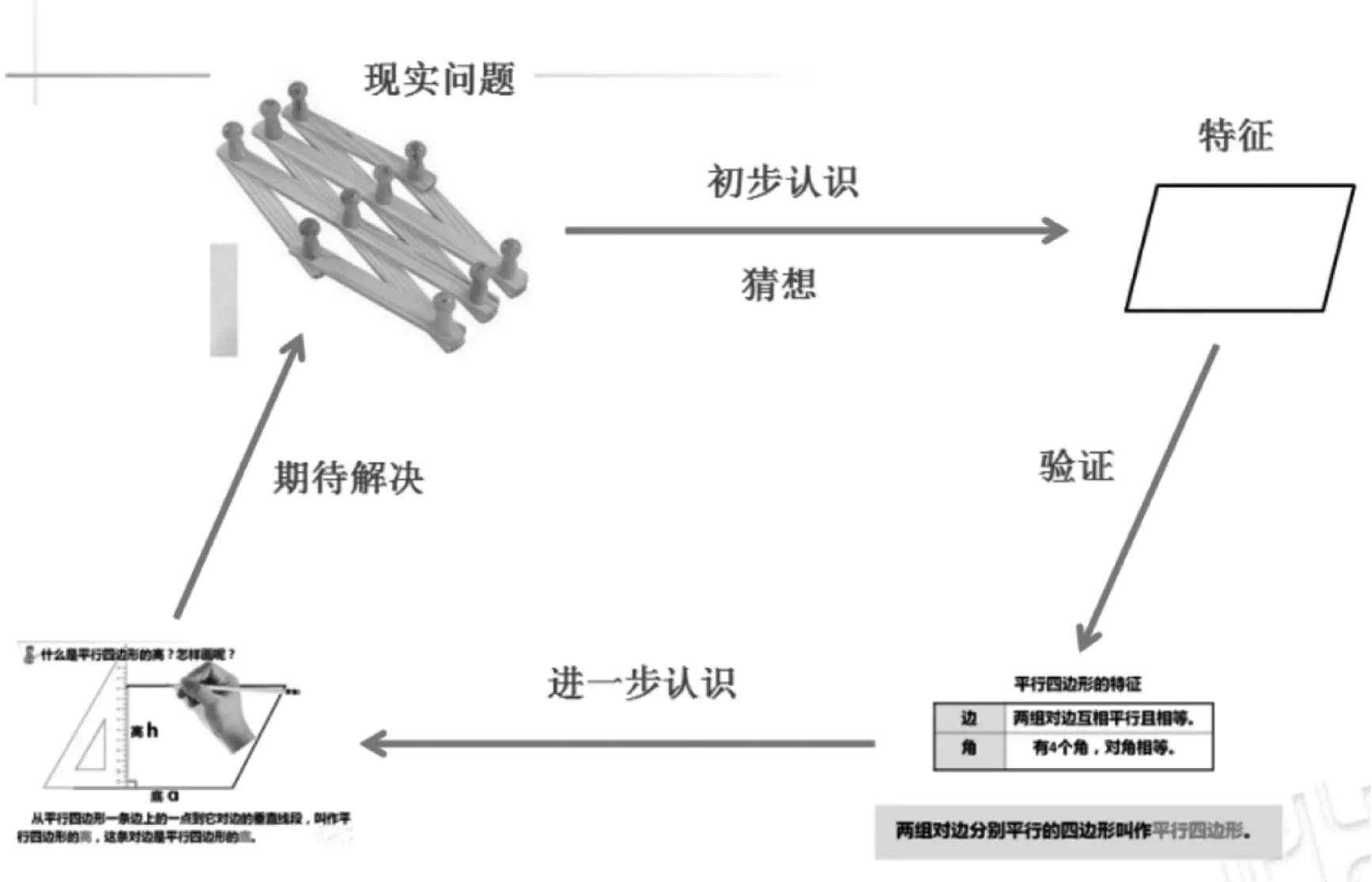
图1

《平行四边形的认识》活动要求

《梯形的认识》活动要求
另外,我们对比《梯形的认识》与《平行四边形的认识》两节课,就可以有更为深入的发现。本节课教师不仅仅是单纯的承接了平行四边形的两条主线,还在承接主线的基础上,有了明显的提升。(1)平行四边形是教师领着猜想,小组验证和得出结论。而这节课是学生完全自主进行猜想、验证、总结。(2)平行四边形教师给每个小组完全相同的平行四边形,而这节课给出了四个不一样的梯形,让学生不仅仅找到每个梯形的特征,还能在汇总时,由特殊到一般,找到共同特征。(3)在研究中为每个小组的3号同学设计了等腰梯形,4号同学设计了直角梯形,为学生自己发现一些特殊梯形的特点做好准备。
单元统整教学中,教师必须要注意的就是“承中有升”。

《平行四边形的认识》探究单
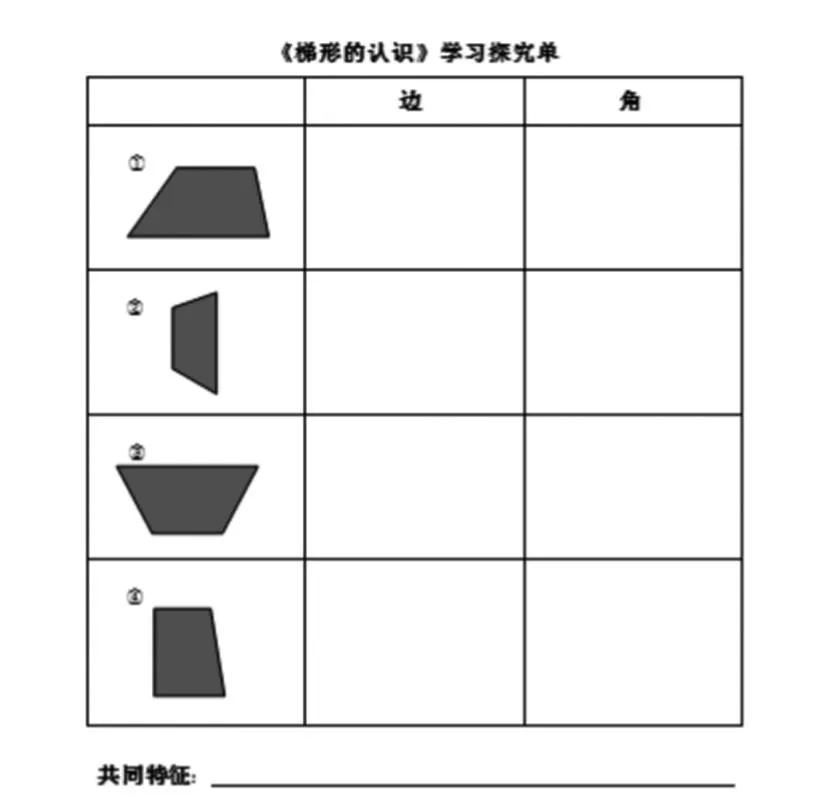
《梯形的认识》探究单
3 合于无声
在这节课的设计中,教师还有几个非常精彩的设计,以小游戏、小策略润物细无声地将一些孩子们学过的平面图形“合”到了一起。
首先,关于平面图形高的“合”。我们说单元统整里的合,就是找到内在联系,抓住本质,总结提升。本节课学生在学习高的时候,教师并没有把重点放在手把手去教孩子什么是高?怎么画高?而是不断的帮助学生建构。从三角形的高、到平行四边形的高、再到梯形的高,发现这些高都是我们四年级上学期:点到线做垂线段的知识。有效的打通了前置知识与新知识之间的联系,正如课堂上学生所说的那样把课本越学越薄。同时,我们这里所说的教学中的“合”,绝对不是简单地知识堆积、累加,而是把每堂课的知识,置身于整体知识的体系中,处理好局部知识与整体知识的关系,让学生在课堂上,积累数学活动经验,让数学变得深刻而厚实。《人民教育》中,曾有这样一段话:教学要有“长程的眼光”,应该把教学过程的每个环节看做是这节课的一个局部,把每节课看作是整个单元或者教学阶段的一个局部,把每个教学单元或者教学阶段看做是整个小学阶段的一个局部。这一点,教师在“单元统整”教学中,要格外引起重视。
其次,剪一刀这个环节,也特别精彩。这里设计了一个学生喜闻乐见的小游戏,同时达成了两个层次的教学目标。(1)回扣梯形定义,而且这里的回扣是两方面的。一方面是,正方形、长方形、平行四边形这样有两组对边平行的,打破一组平行得到梯形。另一方面,三角形从没有平行,到添加一组平行。从三边形剪出四边形。这样的设计,对学生夯实概念再好不过了!(2)学生在剪中,发现了我们所学的这些平面图形的区别和联系,非常巧妙的把这些图形串联在一起。这样的设计,将本节课推向了高潮。
这样的两个“合”,丝毫没有刻意为之,但是当学生每次回头看的时候,都会豁然开朗,都会有一种强烈的“顿悟感”,真是匠心独具。
当然,在“单元统整”的教学研究中,还有很多课型、内容都值得我们进行研究,我们只有找准目标、布好全局,才能像老师们今天研究的这样,真正做到“承中有升,合于无声”。

