线性代数教学中渗透数学建模思想的探讨

朱清芳 周慧倩

（洛阳师范学院数学科学学院 河南·洛阳 471934）

线性代数是大学数学的一门基础课，内容多，比较抽象，如果按传统的教材和教法，直接介绍定义，定理，计算，学生不清楚概念从何而来、学为何用，容易产生枯燥，难懂的想法，学习兴趣和动力不足，学习效果不好。

事实上，线性代数的很多概念如多项式、行列式、线性方程组、矩阵、线性空间等都可以找到相应的实际问题，作为概念的实例引入，反过来又可以用代数概念和方法来解决实际问题.这样，不但能提高学生的学习兴趣，使他们更好的理解代数概念，而且能体验到探索、发现和创造的过程.在实际教学过程中，无论是在数学概念的讲解中，还是在对问题的分析以及思维的拓展上，不断的、反复的强调数学建模的思想，将数学建模思想融入到每一个教学细节上，不论是对我们学生掌握好数学知识，还是培养创新思维能力，都是很好的实践手段.下面从概念引入和理论应用两个方面举例加以说明。

1 概念的引入

很多线性代数概念都具有明显的几何或者实际生活背景，如果从背景出发，通过实际问题建立数学模型来引入代数概念，将很大程度上减轻概念的抽象性，使学生更好的理解概念，激发学习兴趣。

行列式，矩阵，线性方程组，特征值，线性空间等概念都可以这样引入。

实例1：矩阵概念的引入。

问题1：某航空公司在A，B，C，D四城市之间开辟了若干航线，如图所示表示了四城市间的航班图，如果从A到B有航班，则用带箭头的线连接A与B，若两城市之间没有航班则不用连线：

则右图可以用矩阵表示为

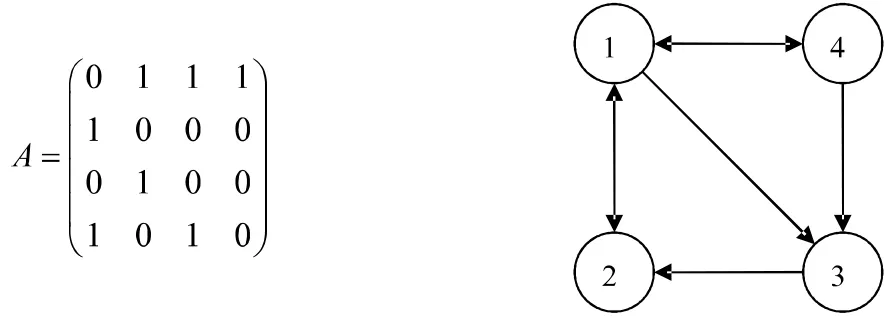
而在实际生活当中，可能会有更多的城市。通过上述矩阵，就可以高效的输入这样一个航班关系图，并且使得计算机能够识别并且快速有效处理这样的图形。

在上面的这样一个实例中，实际上已经应用了如下数学建模手段：图的概念引入；将图转化为矩阵的思想。

问题2：讨论一个两人零和对策问题.两儿童A，B玩游戏，每人只能在{石头，剪刀，布}中选择一种，当A，B各选择一种策略时，就确定了一个“局势”，也就定出了各自的输赢，规定胜者得1分，负者失1分，平手各得零分，则A的得益可用下述矩阵表示：

实例2：矩阵特征值和特征向量概念的引入。

问题：一种昆虫，第一组为幼虫（不产卵），第二组每个成虫在两周内平均产卵100个，第三组每个成虫在两周内平均产卵150个。假设每个卵的成活率为0.09，第一组和第二组的昆虫能顺利进入下一个成虫组的存活率分别为0.1和0.2.假设现有三个组的昆虫各100只，计算第2周、第4周、第6周后各个周龄的昆虫数目，并考虑下面问题：

（1）以两周为一时间段，分析这种昆虫各周龄组数目演变趋势.在两个相邻的时间段，各周龄组的昆虫数目变化的比例是否有一个稳定值？昆虫数目是无限增长还是趋于灭亡？原因是什么？

（2）如果使用一种除虫剂可以控制昆虫的数目，使得各组昆虫的成活率减半，问这种除虫剂是否有效？

对上述昆虫繁殖问题建模解答中，主要使用的是莱斯利矩阵模型以及莱斯利矩阵的特征值。

2 理论的应用和思维的拓展

实例3：动物数量的按年龄段预测问题。

问题：某农场饲养的某种动物所能达到的最大年龄为15岁，将其分成三个年龄组：第一组，0～5岁；第二组，6～10岁；第三组，11～15岁.动物从第二年龄组起开始繁殖后代，经过长期统计，第二组和第三组的繁殖率分别为4和3.第一年龄和第二年龄组的动物能顺利进入下一个年龄组的存活率分别为12和14。假设农场现有三个年龄段的动物各100头，问15年后农场三个年龄段的动物各有多少头？

问题分析与建模：因年龄分组为5岁一段，故将时间周期也取为5年，15年后就经过了3个时间周期。设表示第k个时间周期的第 i组年龄阶段动物的数量（k=1，2，3；i=1，2，3）。

因为某一时间周期第二年龄组和第三年龄组动物的数量是由上一时间周期上一年龄组存活下来动物的数量，所以有

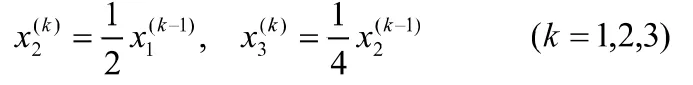
又因为某一时间周期，第一年龄组动物的数量是由于一时间周期各年龄组出生的动物的数量，所以有

结果分析：15年后，农场饲养的动物总数将达到16625头，其中0～5岁的有14375头，占86.47%，6～10岁的有1375头，占8.27%，11～15岁的有875头，占5.226%.15年间，动物总增长16625-3000=13625头，总增长率为13625/3000=454.16%。

这样一个问题是为了引入矩阵的相似对角化计算矩阵的方幂而提出，而实际生活当中还有许多类似的问题，比如人口的迁移问题、就业人员的流动问题等等。

实例4：行星轨道计算问题。

问题：一天文学家要确定一颗小行星绕太阳运行的轨道，他在轨道平面内建立以太阳为原点的直角坐标系，在两坐标轴上取天文测量单位（一天文单位为地球到太阳的平均距离：1.4959787×1011m）.在5个不同的时间对小行星作了5次观察，测得轨道上5个点的坐标数据如下表：

?

由开普勒第一定律知，小行星轨道为一椭圆.请建立小行星轨道的方程：

并确定椭圆的焦点坐标，长轴，短轴的长度。

对如上实例的求解实际上是解一个线性方程组，但我们在课堂上提出了这样的问题，就实际意义而言，观测数据总是有误差的，因此，观测的数据越多对我们计算越有利，但是若有更多的数据，则得到的方程组可能无解.然后由此引入线性回归最小二乘数学模型：在实际生活当中有些问题没有理论上的数学解，但是应用已有的数学知识，我们仍然可以通过数学方法得到需要的解。另一方面，计算椭圆的焦点坐标，长轴，短轴的长度乃是线性代数的二次型理论在解析几何进而在实际问题中的一个典型应用.通过这样一个实例让学生体会到数学建模的无处不在，高等代数在数学模型求解当中的一个又一个的应用。

数学建模方法能够使数学知识形象化、系统化和实用化，同时数学建模思想是学习数学的催化剂和认识理论规律的有力武器.在高等代数的一些概念、定理的教学中渗透数学建模思想，有助于分清各知识脉络以及它们的联系，数学建模思想能将知识向深度和广度延伸，高等代数中有许多具体问题和定理还值得深入挖掘其中的知识点；与其它学科相结合方面的问题也有待进一步探讨。