微吹气对湍流平板边界层流动特性的影响及其减阻机理

范云涛，张阳，叶志贤，邹建锋，郑耀

浙江大学 航空航天学院，杭州 310027

飞机在飞行的过程中，由于大气与机身相互作用，会产生较大的摩擦阻力，导致油耗增加及大量能量消耗。据统计，一架A340客机每减少1%的阻力，每年可以节省40万升燃油[1]。为了减小壁面摩擦阻力，许多主/被动的湍流边界层控制方法被提出，并迅速成为众多学者研究的热点，例如壁面振动器[2]、横向行波控制[3]、沟槽[4]、表面超疏水涂层[5]等。尽管如此，由于湍流的复杂性和减阻效果的适应性，这些减阻方法的内在机理还没有被完全掌握。

微吹气技术(Micro-Blowing Technology，MBT)是一种利用壁表面微小阵列气孔向流场喷入少量气体，试图达到减阻效果的主动控制手段，它由NASA格伦研究中心研究员Hwang和Biesiadny首次提出[6]，并在先进喷嘴和发动机部件的减阻评估中得到成功运用，局部摩擦阻力减小可达50%～70%[7]。区别于一般的吹气方式(如均匀或非定常吹气)[8-9]，微吹气技术最显著的特点在于吹气孔径十分微小，量级通常在0.2 mm左右(如NASA-PN3孔板直径为 0.254 mm)，因而需要的吹气量相对主流来说非常少。但与此同时，由于孔径窄小，阵列布置的多孔板制造加工也成为了一个难题，如何在零吹气情况下保证较小的表面粗糙度，这对制造工艺提出了更高的要求，一系列多孔板例如PN2、PN3、GAC2002-2005等相继被设计和推广[10]。

过去几十年间，Hwang团队针对微吹气技术作了一系列实验方面的研究，用于加深对该项技术内在机理的理解和应用推广[11]。考虑多孔板构型如开孔形状、孔径、孔隙率、长径比、表面粗糙度等结构参数[12]在不同吹气系数条件下减阻效果的差异，虽然可以通过开孔和布局优化使得减阻效果达到最佳，但需要考虑工艺和制造成本，发现PN2和PN3多孔板相比GAC板具有较小的零吹气摩擦阻力，因此可认定为较佳的微吹气孔板选择。随着吹气系数从0增加到0.007 5，多孔板表面减阻率逐渐增加，最后趋于平稳，其中PN2板在低来流马赫数Ma=0.3工况下最大减阻率达到60%，其减阻效果在相同吹气工况下优于PN3和GAC1897[10]。并且，Hwang发现微吹气技术在超声速(Ma=1.9)湍流边界层实验条件下的减阻效果优于亚声速来流工况(Ma=0.3，0.7)，局部减阻率可以达到90%[13]。

在Hwang实验研究基础上，俄罗斯科学研究院Kornilov和Boiko[1]通过较低微吹气流量下的实验，探讨了微吹气对湍流边界层属性的影响，发现速度型U+-y+曲线被微吹气上抬，边界层位移厚度和动量厚度沿着吹气区域发展而线性增加，表面局部摩擦阻力最大可减少70%,整个平板的阻力减少可达4.5～5%；他们还发现在微吹气结束区域的下游，平板表面的摩擦阻力并不能立刻恢复至未吹气之前的状态，这使得减阻效果可以向下游延续一小段距离。针对这种现象，他们研究了间隔微吹气控制对于减阻效果和能量利用率的影响，再次验证了微吹气带来的减阻效果“记忆功能”[14]，在相同吹气流量下，间歇吹气可以改善减阻效果，整个平板净阻力减小可到15%～25%[15]。事实上，关于间歇吹气方式在均匀吹气减阻研究中就有体现，Kametani等[16]研究发现间歇吹气在保证局部减阻率的情况下，可以带来整体更大的能量节省率。中国研究人员在数值模拟方面作了较多的研究工作，李舰等[17]考虑微吹气通道的影响，运用雷诺平均方法数值模拟了微吹气控制下平板边界层流动过程，重点关注了在微孔附近来流气流与微吹气流之间相互作用，并开展了不同微孔板几何和物理条件的参数化研究[18]，尽管其数值计算结果与NASA格林中心的试验数据差别较大,但所做工作对于微吹气通道设计和减阻技术应用来说也起到一定指导作用。此外，他们还建立了微孔壁吹/吸流动系统模型，并通过对数值求解器耦合计算，提高了微吹吸流动控制在数值模拟方面的计算精度[19]。

微吹气技术在实验和数值模拟中均展现出了较好的减阻效果。但到目前为止，尽管国内外关于吹气减阻控制方面研究很多[20-21]，但关于多孔阵列下微吹气技术的研究还比较少，Hwang和Kornilov等的研究成果也大都局限在对减阻率的强调上，而对减阻机理和壁湍流特性的关注比较少，特别是采用雷诺平均方法对壁湍流结构进行解析，精度往往是不够的，以至于人们对微吹气技术的认识和理解还很有限。因此，本文试图运用一种高精度有限差分求解器，更精细地对微吹气控制下空间发展湍流边界层进行直接数值模拟(DNS)，并通过与未加控制的光滑平板边界层算例进行对比，重点关注近壁区湍流边界层流动属性的变化，进一步挖掘微吹气控制下湍流结构的演化规律，这对于加深理解微吹气减阻机理具有重要的意义。

1 光滑平板湍流边界层基本算例

1.1 计算模型及方法

在数值计算中，通过求解三维直角坐标系下可压缩Navier-Stokes方程，对空间发展的平板湍流边界层进行直接数值模拟。DNS求解器采用李新亮开发的Hoam-OpenCFD有限差分数值软件，对流项离散采用七阶精度迎风差分格式，扩散项采用八阶精度中心差分格式，并在时间项处理上运用三阶TVD型龙格-库塔方法进行推进。在该算例中，除特别说明外，所有物理量均采用相应自由来流参数进行无量纲化(符号∞为自由来流)，特征长度为1 in(1 in =2.54 cm)。

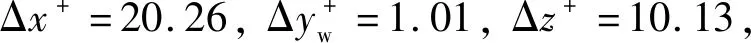
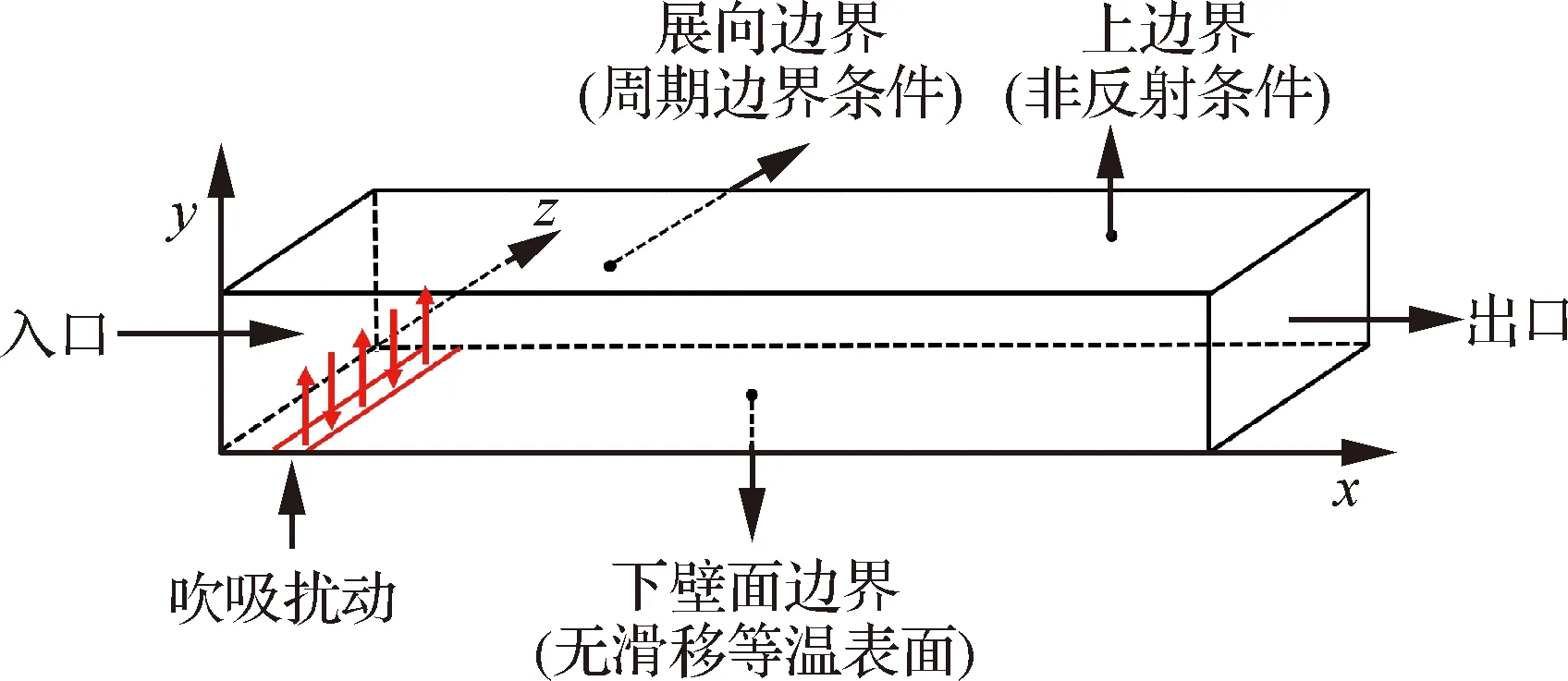
图1 计算平板示意图Fig.1 Sketch of computational flat plate

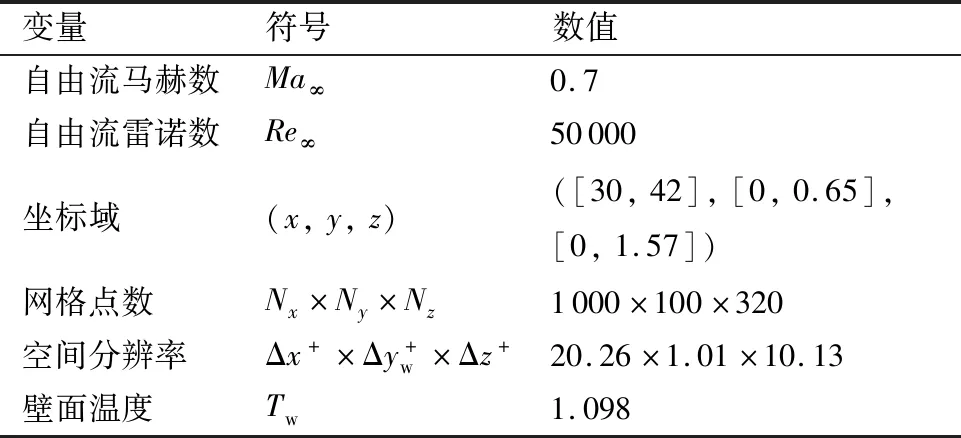
表1 计算参数Table 1 Computational parameters

为了加速层流-湍流转捩过程，在图1中靠近进口区域采用局部交替吹吸气(B/S)控制[25]，壁面法向扰动速度分量定义为

v(x,z,t)=Au∞f(x)g(z)h(t)xa≤x≤xb

(1)

式中：f(x)、g(z)、h(t)分别表示流向和展向2个方向以及时间控制的函数。

(2)

(3)

(4)

经过反复测试，以寻求成功激发湍流转捩的最小扰动。最终计算中，扰动振幅A取为0.12，坐标xa和xb分别是局部吹吸区的起点和终点，是吹吸区的展向长度，干扰频率β为75 000 Hz，随机数φl和φm的范围是0～1。

1.2 计算结果及验证

在气流达到统计平稳状态后，计算时空湍流的统计量。图2为y+=3.11的黏性底层中湍流结构的空间分布。虚线框表示带B/S的转捩控制区域。需要强调的是，这里B/S控制的目的与后面研究的微吹气控制目的不同，这里只是为了加速湍流转捩。3个时刻的法向速度分量v在B/S区域内周期性演化如图2x-z平面所示。在B/S控制下游逐渐出现一些条纹结构，猝发了流动的不稳定，预示着入口层流受到吹吸气扰动正在发生转捩。

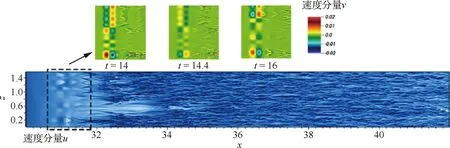
图2 y+=3.11处x-z平面的速度云图Fig.2 Velocity contours in x-z section at y+=3.11

图3显示了u′的瞬时能谱E(u′u′)沿x方向的变化。高、低波数kx分别代表小尺度和大尺度的脉动结构(波长为1/kx)。在B/S区域(x=30～32)，由于吹吸气控制(扰动最大幅值vmax=0.12)引入了许多大尺度结构，因此低波数扰动(kx=2,4)能量占主导部分;随着转捩的发展(x=32～34)，高波数的扰动被激发，小尺度运动逐渐增强;在x>34区域，各种尺度的波动结构和能量分量达到相同的量级，最终形成宽带谱。这表明该流动已发展为多尺度湍流边界层流动。

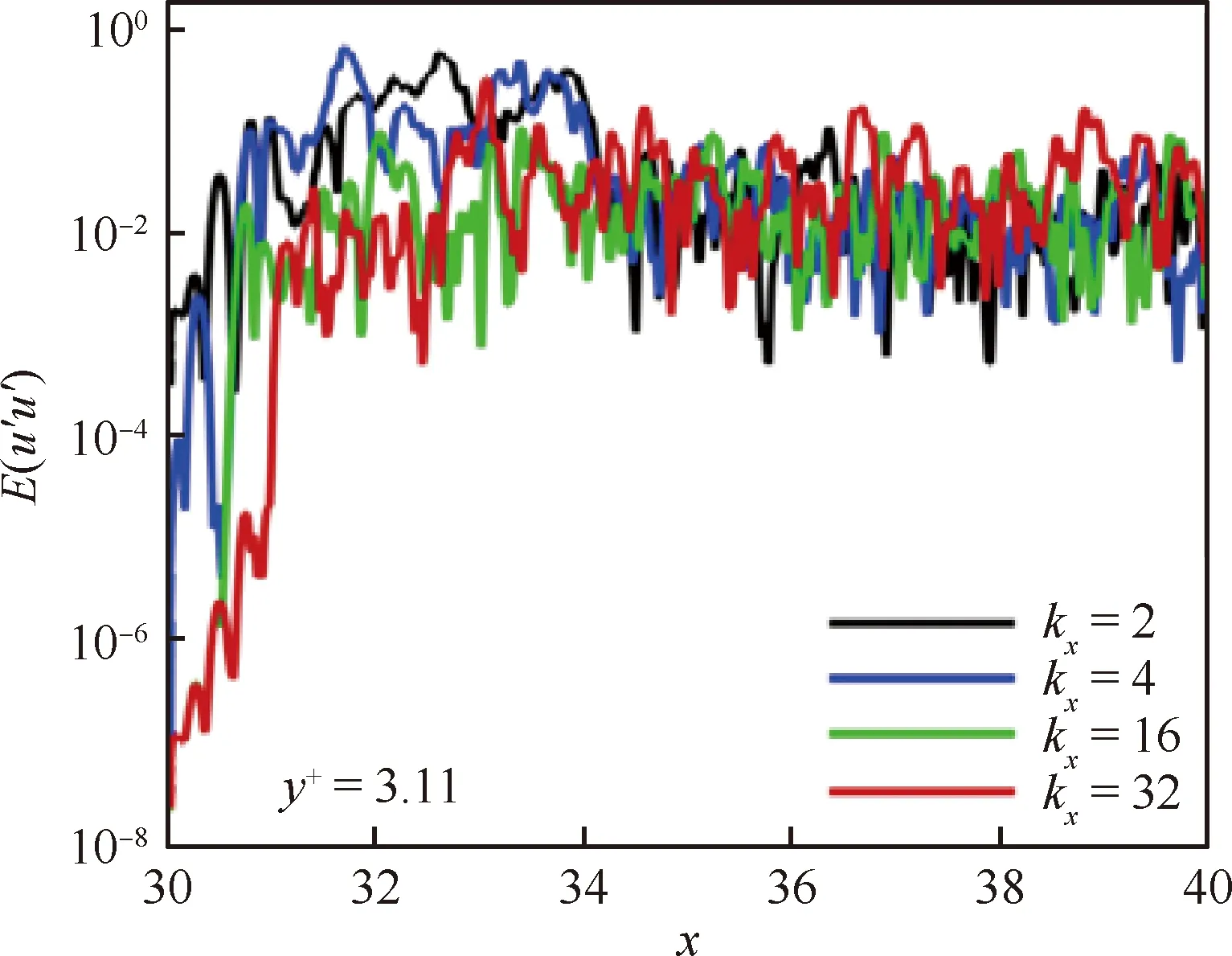
图3 沿流向脉动速度的能谱Fig.3 Energy spectrum of streamwise fluctuation velocity

湍流强度沿壁面法向方向的分布如图4所示。其中，urms(实验)、vrms(实验)、wrms(实验)分别表示文献[26]实验数据中的流向、法向和展向的速度脉动均方根，urms(DNS)、vrms(DNS)、wrms(DNS)则代表本算例的结果。在近壁区，流向湍流脉动占主导地位，法向方向的脉动最弱，突出了湍流的各向异性。逐渐远离壁面，各速度分量的均方根值趋于均匀，表明边界层外层湍流的脉动趋于各向同性。当前计算结果与实验数据符合较好[26]，这表明当前的数值方法和计算模型可以准确地预测湍流结构的脉动信息。

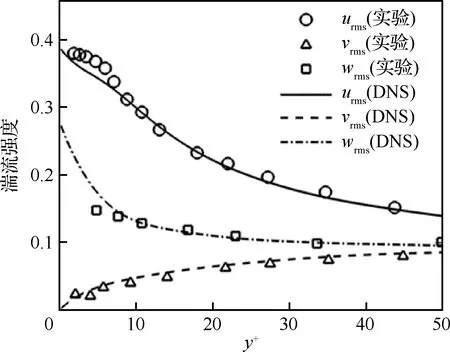
图4 速度脉动的均方根Fig.4 Root Mean Square (RMS) of velocity fluctuations

图5显示了3个时刻湍流相干结构的演化过程，其特征用速度梯度张量的二阶不变量Q2来表示。由于入口B/S扰动，下游开始形成一系列的流向涡和发夹涡结构。在初始阶段，发夹涡旋被周围层流包围，因此它们被限制在一个小的局部区域。但由于湍流脉动与周围层流的相互耦合，会使剪切层非常不稳定[27]，因而层流开始失去稳定性，并且在发夹涡流的影响下，流向和展向不稳定区域的面积也在逐渐增加，最终导致了下游区域大面积发卡湍流涡结构的形成，这与Head 和 Bandyopadhyay[28]的流动可视化结果一致。

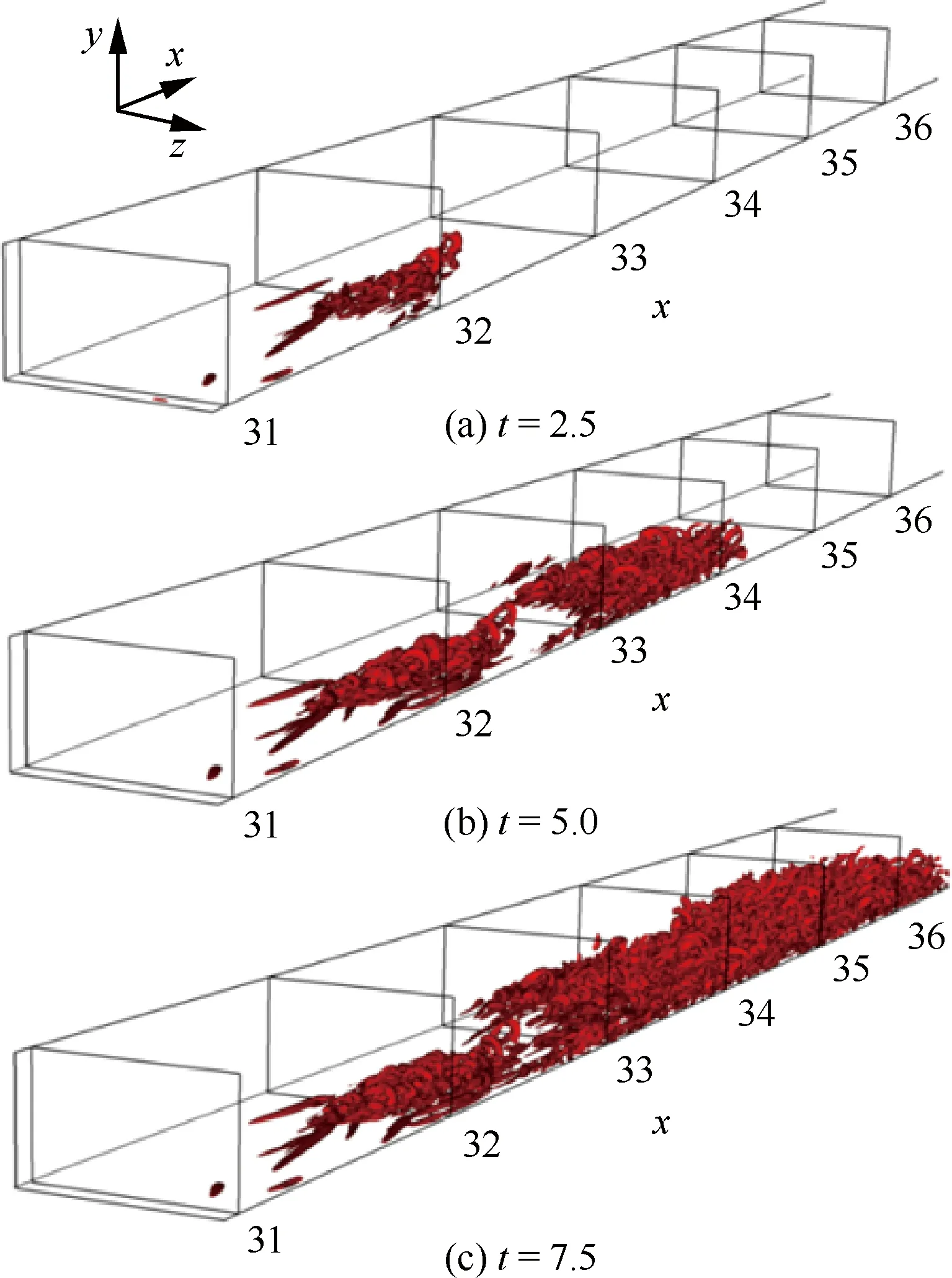
图5 在t=2.5，5.0，7.5时刻Q2=10的涡结构Fig.5 Vortex structures of Q2=10 at t=2.5,5.0,7.5

2 施加微吹气流动控制

2.1 计算模型

在上述光滑平板湍流边界层算例分析的基础上，考虑到在x≥36区域，边界层流动已经转变为空间发展湍流结构，因而在此区域施加局部微吹气控制，如图6所示。采用了无量纲直径为0.006 5的NASA-PN2多孔平板[10]。微孔的布置为16×16的交错阵列，并从左到右依次编号。相邻孔的中心间距h=0.008 5，保证了23%的孔隙率。为了直接数值模拟的方便，省去了实际微孔通道的影响，通过壁面边界条件的施加来实现微吹气控制。

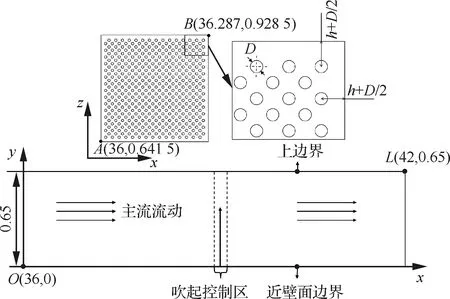
图6 微吹气示意图Fig.6 Sketch of micro-blowing model

大质量射流会带来流动分离，造成较大的表面摩擦损失，降低能量利用效率。在微吹气控制中，吹气系数F=0.001 5(F=ρjVj/ρ∞u∞，Vj是微吹气气体从壁面法向喷射的速度)，微吹气体密度ρj与来流气体密度ρ∞之比DR=1.2，吹气温度选取为Tj=0.868，略小于自由流。考虑到微吹气孔尺寸，需要细化网格来解析微吹气孔附近的小尺度湍流结构。局部网格点的布置保证在一个微孔直径范围内占据8个节点,因而微吹气阵列区域网格尺寸取为0.068Δx(Δx是基础算例中网格的大小),并且加密区域向阵列外多扩展一个h+D/2距离，以便在微孔附近获得更详细的流场特征。最终，网格节点总数达到1 232 ×100×416，约5 100万，如图7所示，具体参数如表2所示。

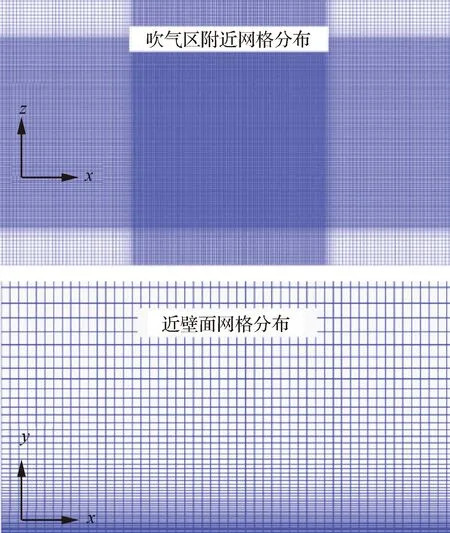
图7 不同方位的网格示意图Fig.7 Schematic diagrams of grid distributions from different perspectives

表2 微吹气算例中的计算参数Table 2 Computational parameters in micro-blowing case

2.2 流场速度分布及摩擦阻力

流体的速度特征对分析流场的性质具有很重要的意义。通过施加微吹气控制技术，流向速度在黏性底层、对数层和边界层外层都有和光滑平板湍流算例不同的特征。

图8展示了距离壁面不同距离的平面高速条带和低速条带的变化。在黏性底层(y+=6.8)，流向速度较低，低速条带呈现细长的状态，并且由于法向吹气射流对自由来流的阻隔作用，在微吹气控制区域(红色框标识)，流向流速低于周围的流体速度，从而呈现出一个明显的白色“局部斑”；在对数层(y+=14.7)，细长条纹开始脉动，并导致头部变形和弯曲，这表明湍流在远离壁面处增大，“局部斑”区域减小，但是在下游仍比较明显。在远离壁面处(y+=32.9)，细长条纹逐渐断裂消失，低速的白色斑点几乎消失。整个过程呈现了壁湍流条纹结构从产生、变形到破碎的过程。

图8 x-z平面瞬时流向速度分布Fig.8 Distribution of instantaneous streamwise velocity at x-z section

图9对比了施加微吹气控制前后光滑平板平均速度型变化，在未施加微吹气控制的光滑平板湍流边界层基本算例中(虚线表示)，x=35.9～36.5的范围内，随着法向距离的增加，不同流向位置处的无量纲速度U+表现出相近的变化趋势，4个取样流向位置处的U+-y+曲线近乎重合，在y+>200时，4个取样的流向位置U+趋于稳定(稳定值在20左右)。而采用了局部微吹气控制之后(吹气区域大小如图6所示，x=36～36.287)，在紧贴吹气控制区的上游位置(x=35.9)，其U+-y+曲线和光滑平板湍流基本算例中同一流向位置几乎重合，这说明微吹气控制对控制区域上游的流场影响很弱；而在控制区域内部以及控制区域下游很近的范围内(图中取样位置分别为x=36.1 和x=36.3)，在y+>10区域，流向平均速度有明显提升，并在外层稳定在U+=25附近，这与Park和Choi[29]得到的结果相一致；远离吹气控制区域(x=36.5)，流向平均速度型下降，略低于光滑平板算例的曲线分布。两条黑色虚线分别代表不可压缩平板湍流边界层内对数律和壁面律分布，与本文直接数值模拟结果吻合较好。

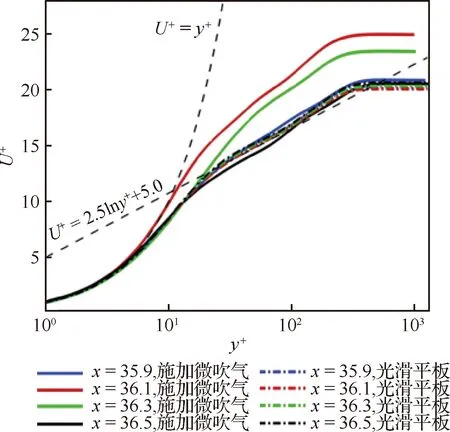
图9 不同流向位置的平均速度型Fig.9 Profiles of mean streamwise velocity at different streamwise locations

施加微吹气控制后，对应着边界层流向平均速度型的上升和低速“局部斑”形成这两种特征，图10对比了光滑平板及微吹气两个算例的壁表面局部摩擦系数分布。壁面摩擦系数Cf和局部摩擦切应力τw的定义方式为

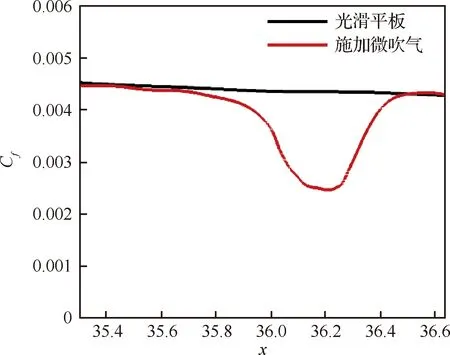
图10 壁表面局部摩擦系数Fig.10 Local friction coefficient at wall surface

(5)

式中：τw为壁面切应力；μw为壁面附近气体动力黏度。注意这里关于壁面切应力的计算均是流向速度U进行时间和展向平均处理后所得的梯度结果。从图中可以看到，在微吹气控制区域，流场的局部摩擦阻力系数有显著的下降，最大的减阻效率达到了45%左右，并且在微吹气控制下游 (x>36.287)，表面摩擦阻力持续了一小段逐渐恢复的过程，最后与基本算例阻力一致，这种减阻效果的“记忆”作用与文献[1]研究结论一致。

虽然从图10中能够明显看到微吹气技术的减阻效果，但是从实际应用的角度来评估控制效率也是很重要的。文献[20,30]介绍了一种计算吹气控制净节能效率S的方法，定义为

(6)

(7)

式中：Cf,nc和Cf,ctr分别代表未施加控制和微吹气控制两种算例下的平均摩擦阻力系数，

(8)

(9)

Lctr为流向微吹气控制区域长度。这里忽略了实际装置中微吹气体的沿程压力损失。通过计算，可以得到施加微吹气后的净节能效率S达到了11.10%，小于文献[20,30]在均匀吹气情况下的净节能效率(12%～18%)，其差异性可能与吹气方式、吹气区域长度、来流雷诺数等因素有关。

从图11(a)流向速度u分布可以看出，在y+<40，边界层速度等值面在经过微吹气区域 (x=36～36.287) 时出现了一个微小的凸起，并且在微吹气的下游位置逐渐恢复至原来状态，这也可以从图11(b)中流线的走势看出，微吹气区域的流线有“向上扬”的趋势。这表明了微吹气控制使得近壁区边界层厚度增加，从而黏性底层内速度梯度降低，壁面摩擦阻力减小。由于黏性底层厚度较小，导致这种变化可视化效果并不十分明显。由以上分析，可以得出在本算例的基础上增加吹气区域面积，能够有效增加减阻区域维持的长度，从而使得整个平板的摩擦阻力呈整体性的下降。但值得注意的是由于微吹气减阻效果的“记忆”作用，也没有必要对整个平板均施加微吹气控制，可以采用间歇控制的手段，以达到最佳最经济的减阻效果。

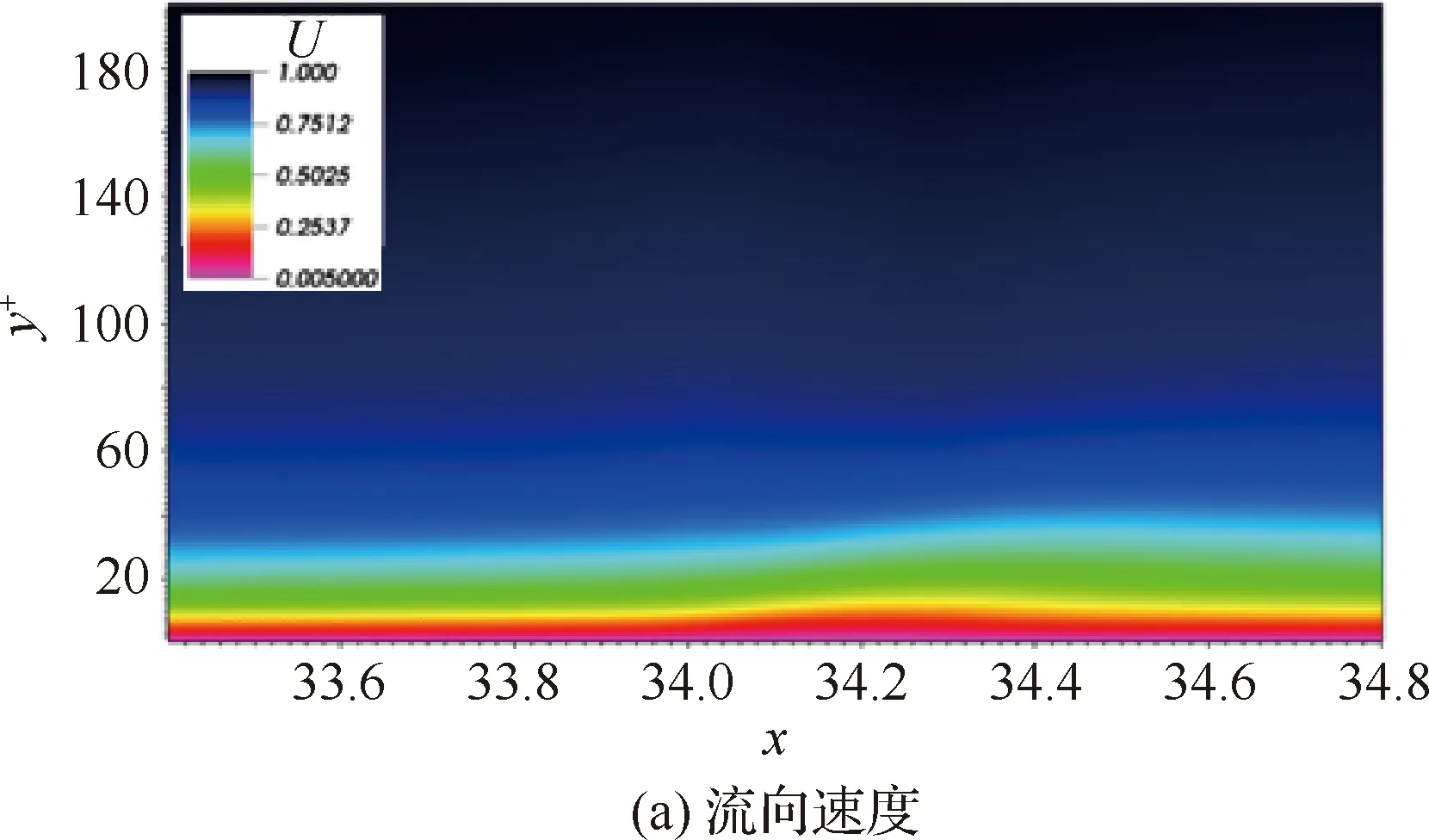
图11 流向和壁面法向速度分布云图(作展向z和时间t平均)Fig.11 Distribution of streamwise and wall normal velocities (time t and space z averaged value)

Kametani和Fukagata[20]通过对壁面摩擦阻力的分解，研究了空间发展平板湍流在均匀吹/吸气控制下的减阻效应，指出当吹气时，边界层内正向对流项(+uv)对壁面减阻起到主导作用，使得近壁区流体有一种向外层运动的趋势，因而边界层厚度增加，平均速度型向上抬升。与均匀吹气类似，本文通过微吹气技术的研究证实了这一点。在微吹气区域出现了相对较高的壁面法向速度v，其最大峰值速度为0.01，近似于微吹气前后速度的10倍，峰值点位置在y+=40左右。这说明微吹气提高了边界层内法向速度分布，使得沿着壁面法向方向产生了一个相对较高的正向对流区域(+uv)，也正是由于这个对流项对减小摩阻起到了增进效果。对于将来的研究工作来说，为了得到更强的减阻效果，可以从增加正向对流区域的角度出发，优化设计出新的微吹气控制手段。

2.3 湍流脉动强度分析

图12是3个方向湍流强度(由速度均方根表示)随法向位置变化曲线，其取样点位置如图13所示。图12(a)、图12(c)和图12(e)展示了从未控制区到控制中心区域的湍流强度演化，可以看出，湍流强度呈现逐渐增强的趋势，并且在进入吹气区域的一定位置之后，流场的湍流强度在某一个固定值附近波动。对比3个不同速度计算的湍流强度来看，在吹气区域内达到的urms峰值相比吹气区域前的湍流峰值增加了52.0%，vrms和wrms的变化相对来说较小，分别为30.6%和38.2%。但湍流强度峰值点所对应的壁面法向无量纲距离基本不变，保持在y+=15左右，这与Kametani等[30]均匀吹气得到湍流强度规律一致。超过峰值点位置，3个方向的湍流强度迅速下降，但控制区回落的速度都要比控制区域前的稍大，这一点在控制区下游也出现了类似情况。随着逐渐远离壁面(y+>160)，控制区域3个方向的速度均方根变化与控制区前后基本吻合。总的来说，微吹气控制在垂直壁面方向引入的气流虽然速度和质量流量都比较小，但是造成的湍流脉动强度增加的程度是比较大的。图12(b)、图12(d)和图12(f)展示的是从吹气区域向吹气区域下游的湍流强度变化情况。在x=36.21之后，流场的湍流强度沿着流向方向，呈现出稳定下降的趋势。本算例中，控制区域的终止线在x=36.287附近，而从图中可以看到，即使是在控制区域的下游(如x=36.37)，3个方向的速度脉动强度均未恢复到未施加控制之前的水平，这一现象说明微吹气技术不仅改变了控制区域的流场性质，而且这一控制手段还通过流场传到了控制区域的下游，并影响了下游一定范围的流场。x=36.28和x=36.37这两个取样点分别处在吹气控制区域及控制区域下游相距很近的位置，但两位置湍流强度差异特别明显，这说明流场保持在较高的湍流强度，需要有壁面吹出的气体维持，一旦离开微吹气控制区域，湍流强度相应地会大幅度减小，但减小后湍流强度仍会维持一小段距离。

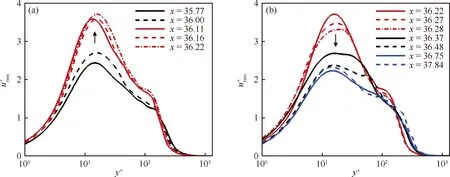
图12 不同流向位置的速度均方根分布Fig.12 Distribution of Root Mean Square (RMS) of velocity at different streamwise locations

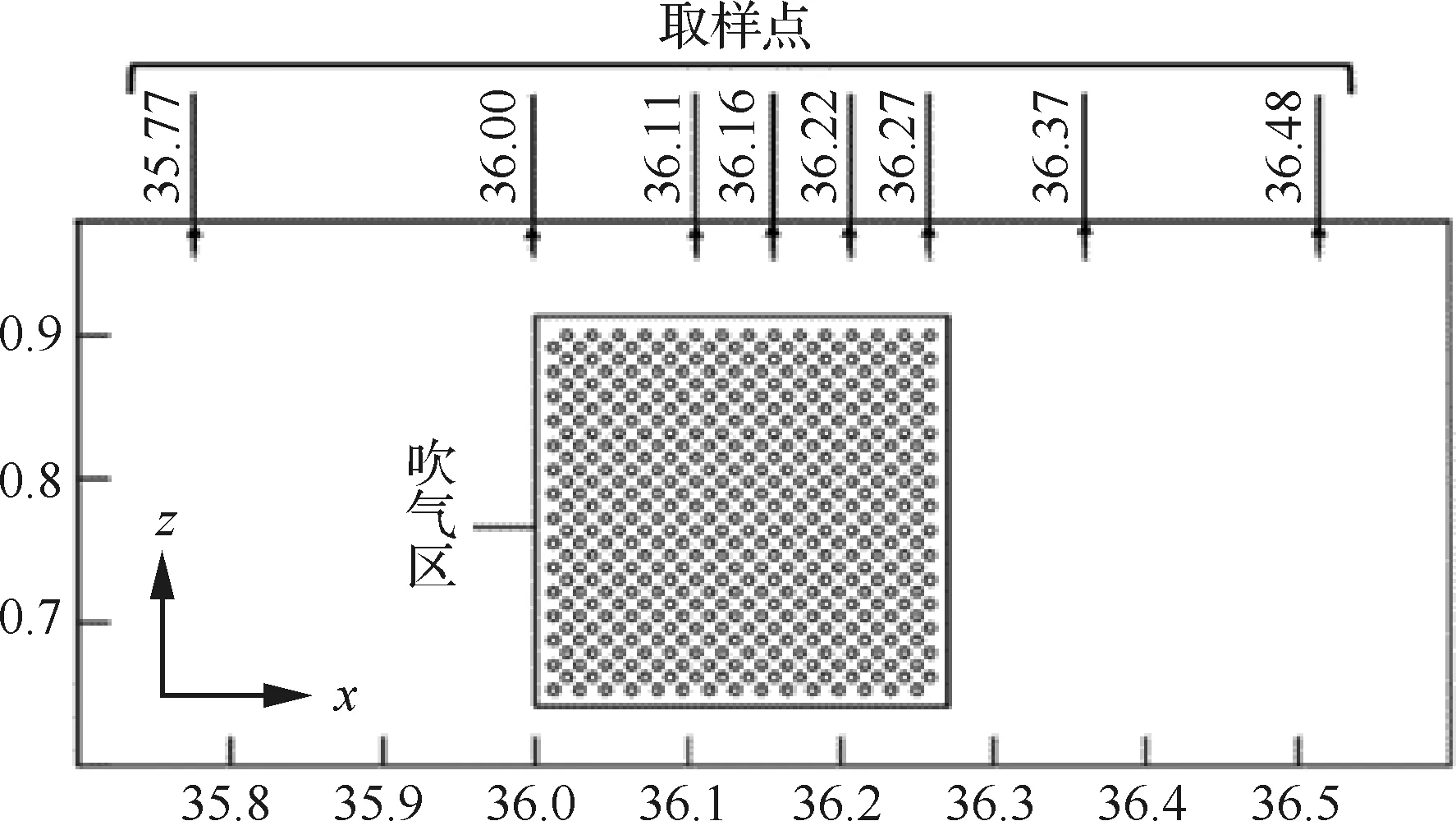
图13 流场取样点示意图Fig.13 Sketch of flow field sample

2.4 流向涡量分布及其变化

图14展示了施加微吹气控制后，湍流边界层内流向脉动涡量沿着壁面法向方向的变化曲线，其中upstream和downstream分别表示靠近吹气控制区域上下游一小段距离的统计平均，far downstream表示控制区域下游较远距离的统计平均。将微吹气控制区域均分成前后两部分，分别作统计平均并用1st 和2nd half of MBT标识。

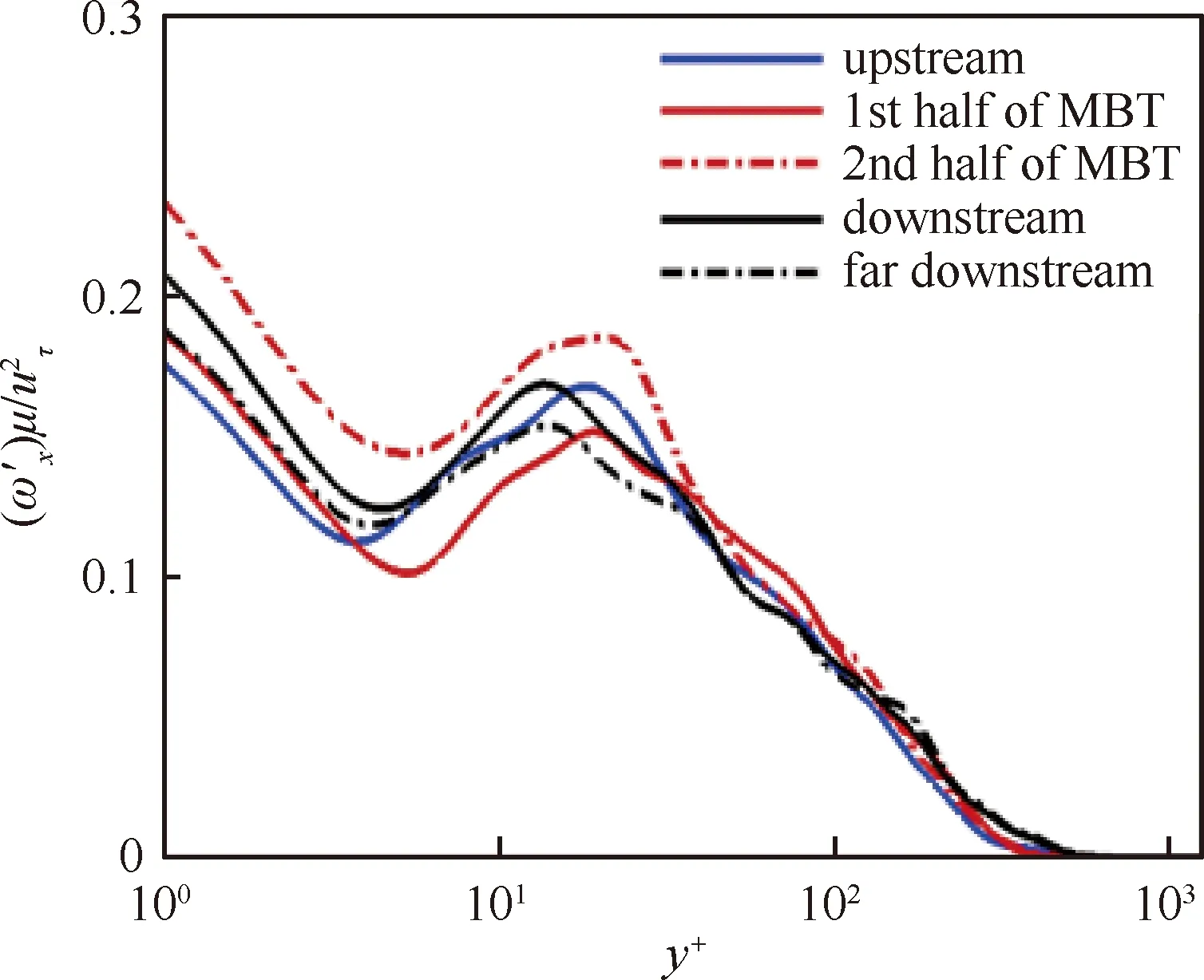
图14 不同流向位置脉动涡量变化Fig.14 Streamwise vorticity at different flow sections

此外，流向脉动涡量统一采用未吹气位置x=34.83处摩擦速度uτ进行相关无量纲化。从总体变化可以看出，流向脉动涡量沿着y+变化，呈现出先减小、再增大最后再减小的趋势。控制区域后半段(2nd)的脉动涡量比上游和下游的脉动涡量大一些，但是控制区域的前半段涡量(1st)和下游相比略小，这是因为受到微吹气影响的流场需要通过一定距离的发展，其流向脉动涡量才能够达到一个比较高的水平。而在吹气结束后，流场的脉动涡量开始逐渐下降，这是因为这些流向脉动涡的存在需要微吹气的维持，否则在流场中由于微吹气控制增加的脉动涡量会随着湍流的发展而逐渐耗散，downstream和far downstream的脉动涡量对比更加突出说明该问题。

图15为施加微吹气控制和光滑平板这两种工况下流向脉动涡量和平均涡量的对比情况。从流向脉动涡量分布可以看出，施加微吹气控制后的流场脉动涡量要有所提高，在吹气控制区域，脉动涡量在其极大峰值点处所对应的y+有所增大，即在吹气区域所达到的最大脉动涡量位置，相比基本算例有向外层移动的现象，说明了微吹气对流向脉动涡起到了抬升作用。这一点从图14中未吹气和吹气区域脉动峰值点位置对比也可以看出。图15(b)中展示了平均流向涡量的变化，流场在经过吹气控制区域的时候，近壁区平均涡量由原来较小负值转变为较大的正值，这是由于微吹射流提高了近壁面处的法向速度(ωx=(∂w/∂y-∂v/∂z)/2)，从而使得流向平均涡量增加。在远离壁面y+>40区域，流向涡量的大小与光滑平板算例大致相同，这也间接说明当前微吹气控制(吹气系数0.001 5)贯穿深度局限在y+<40范围内。

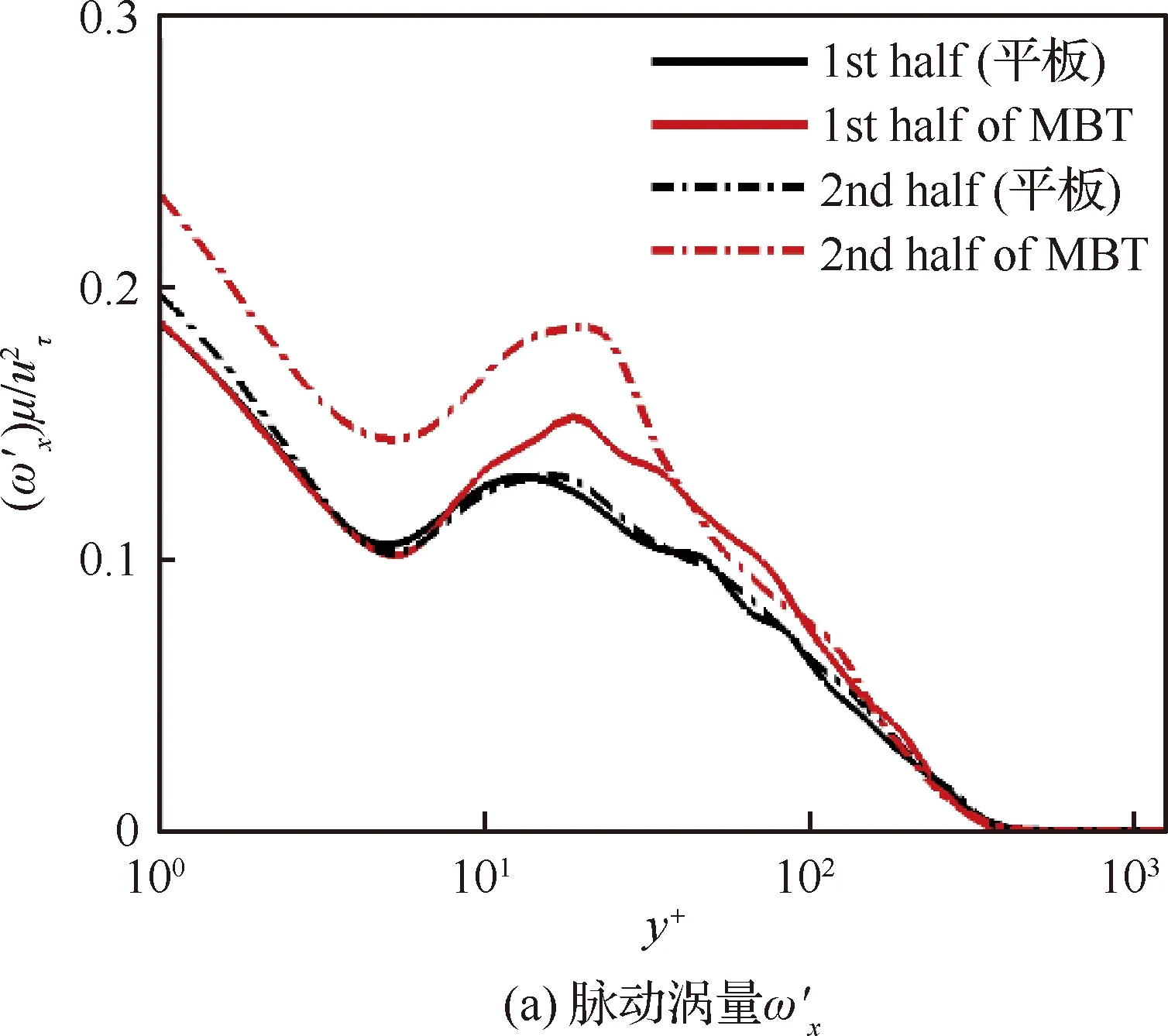
图15 不同工况下脉动涡量和平均涡量的对比Fig.15 Comparison of streamwise vorticity fluctuations and averages in different cases

图16对比了不同流向x截面的流向脉动涡量分布云图。对吹气前后展向位置(图16(a)和图16(d))而言，微吹气区域(图16(b)和图16(c)中黑色虚框)的流向脉动涡分布较为散乱，涡团结构也相对细碎，特别是在紧贴壁面y=0附近，流向涡并没有如图16(a)、图16(d)一样紧贴壁面运动，正如前面定量分析那样，涡团结构被微吹气流所抬升，这样直接减少了流向涡与壁面之间的相互作用。

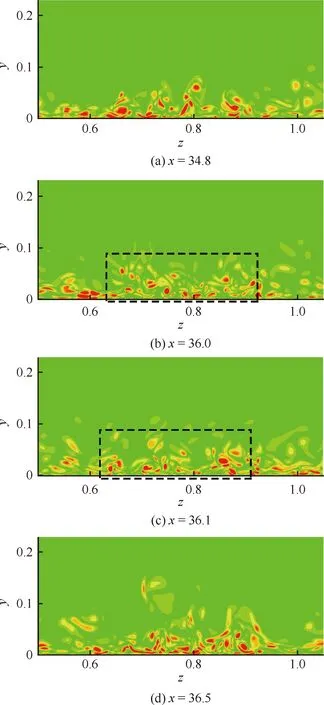
图16 不同x截面流向脉动涡量分布Fig.16 Distribution of fluctuating streamwise vorticity at different x cross-sections

图17展示了3个时刻3维流场涡结构在近壁区附近的演化过程，可以看出微吹气流在流场中呈现出多孔“圆球状”的阵列涡结构，这种结构对近壁流向涡会产生一种冲击作用，并在流向涡表面留下印记，如图中白色圆圈标识。在t=14.5，近壁流向涡(图中A标识)流过微吹气区域时，在微吹射流的冲击作用下，“长条状”涡结构会被分散成小的涡团结构(t=15.5)，并在涡表面留下一个个冲击坑痕，小的涡团结构在向下游运动过程中(t=16.5)，不断受到微射流的冲击，进而演变成更散乱、细小的涡结构，如图16所示。在远离微吹气下游，由于没有吹气的作用，流向涡结构有恢复至微吹气之前的状态。

为了研究微吹气控制在动力学层面对流向涡的影响，下面考虑流向涡量随时间演化的输运方程：

(10)

式中：d/dt=∂/∂t+uj∂/∂xj。

方程(10)等号右边第1项代表拉伸项，第2项代表倾斜项，第3项代表扩散项。将方程(10)的左右两边同时乘以ωx，得到关于流向涡能的动力学方程：

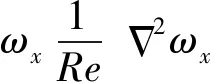
(11)

通过研究流向涡动力学方程(11)等号右边各项的大小，可以知道拉伸项、倾斜项和扩散项这 3项中对流向涡影响比较显著的因素。

图18为流向涡能动力学方程中各项大小随y+的变化而变化的曲线图，实线代表的是施加微吹气后的算例，点画线为光滑平板算例。先从微吹气算例(实线)来看，210之后，扩散项和倾斜项的贡献逐渐减少，拉伸项的贡献超过了倾斜项，并在y+=15处达到峰值。此时，拉伸项和倾斜项的贡献和大于扩散项，从而使得它们的和大于零(尽管幅值较小)，表明流向涡能量在此区域随时间演化正在累积。在对数律层(y+=15～35)区域，扩散项贡献下降的速度依然相对较快，这3项之和仍然保持在较小的正幅值。当逐渐远离壁面(y+>35)，这些项的贡献变得十分小并趋于0。从上述各项的变化规律可以看出，流向涡量的扩散项在黏性底层占据最主导地位，伴随着流向涡能的不断耗散，拉伸项在对数层起到了关键作用，导致流向涡强度随时间演化得到了增强。

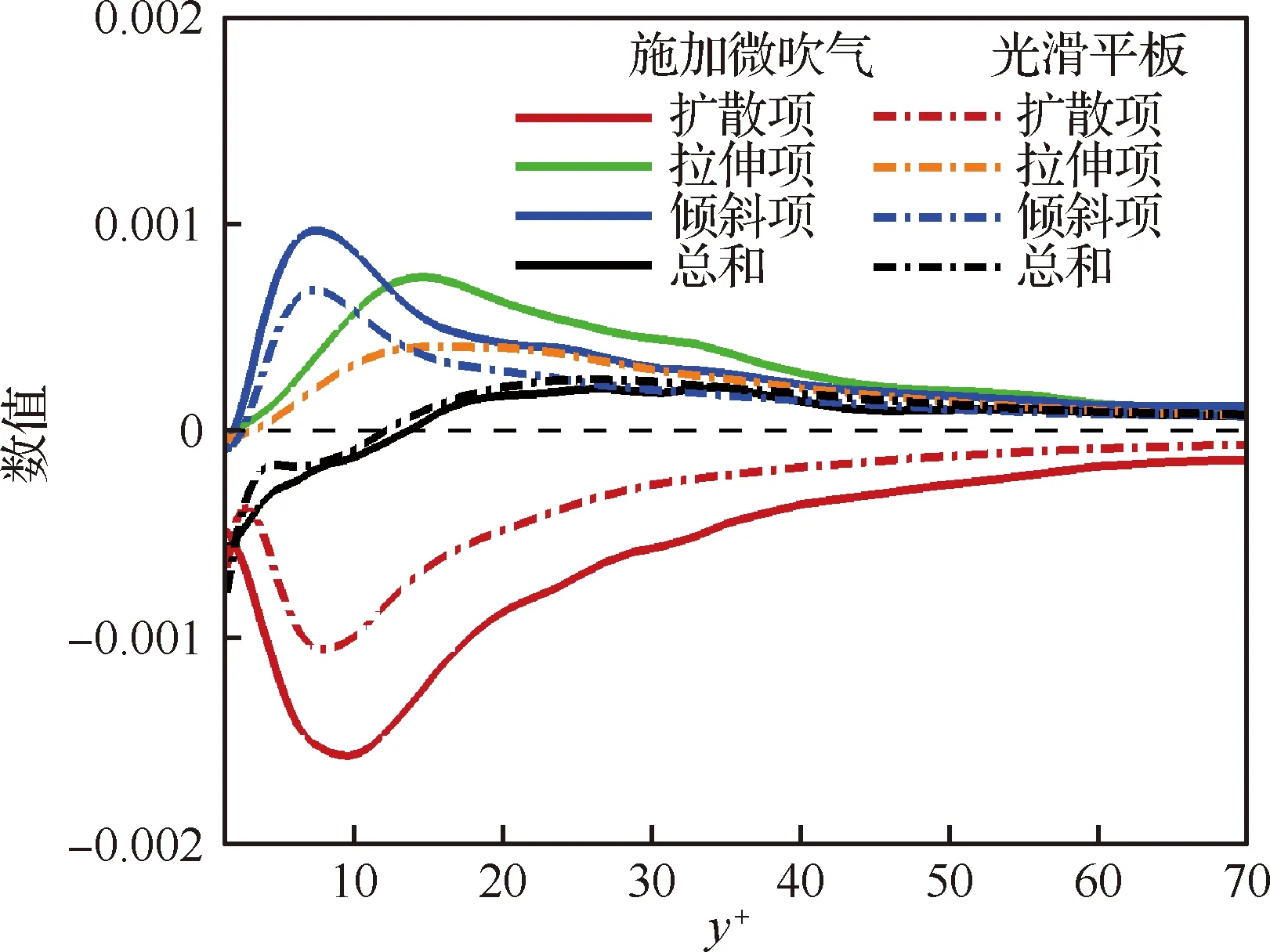
图18 涡量输运方程各项贡献Fig.18 Terms of streamwise vorticity equation

对比两个算例，微吹气工况下流向涡输运方程各项在数值上都比平板算例中各项的数值大，这说明微吹气对流体质点的拉伸和倾斜运动起到促进作用，增加了流向涡量；但与此同时，吹气带来分子扩散加剧导致流向涡的耗散也增加，因此这两种工况下各项之和几乎重合，表明微吹气对流向涡能的整体时间演化影响不大。对比各条曲线峰值点位置，可以观察到倾斜项和扩散项峰值点位置在微吹气控制的影响下均有向外层移动的趋势，这表明流向涡运动的部分属性被微吹气控制所抬升。此外，注意到在黏性底层(y+=4)附近，光滑平板算例的扩散项曲线(红色点画线)出现一个小的凸起，进而导致总和曲线同样出现了一个凸起，这是由扩散项二阶导数在壁面边界处离散处理导致的。

3 结 论

本文基于NASA-PN2多孔板几何参数，运用一种高阶精度有限差分求解器对自由来流Ma=0.7 条件下空间发展平板湍流边界层流动进行了直接数值模拟，验证了微吹气技术在湍流边界层减阻方面的有效性。并通过与不施加控制的光滑平板湍流边界层进行对比分析，进一步分析微吹气控制区上游和下游区域的湍流流场性质，可以得到以下结论：

1) 施加微吹气控制后，速度型曲线在对数律层会向上抬升，且在吹气区域下游逐渐下降并恢复至未施加控制之前的状态。这表明微吹气使得近壁区边界层厚度增加，黏性底层内速度梯度降低，因而起到降低壁面摩擦阻力的效果，其局部最大减阻率达到45%，并且微吹气控制会产生一个“记忆”功能，使得减阻效果向下游持续一小段距离，增大了有效减阻区域的流向面积。此外，局部的微吹气控制会使得近壁区产生一个低速的“局部斑”，且该斑点面积沿着壁面法向逐渐减小。

2) 微吹气使得边界层湍流强度呈现逐渐增强的趋势，并在进入吹气区域一定位置之后，流场的湍流强度在某一个固定值附近波动，其中u、v、w3个方向脉动峰值相比吹气区域前分别增加了52.0%、30.6%和38.2%。与减阻的“记忆”功能类似，一旦离开微吹气控制，湍流强度相应地会大幅度减小，但减小后湍流强度仍会维持下游一小段距离。

3) 微吹气对流向脉动涡发挥着多重作用，不仅增加了流向涡的脉动强度，而且还使得流向涡团向上抬升，这样直接减小了流向涡与壁面之间相互作用，有利于减小摩擦阻力。再者，微吹射流对流向涡产生的冲击作用，使得流向涡分散成相对小的涡团结构，并在其表面留下了凹痕。

4) 流向涡量输运方程中扩散项在黏性底层占据主导地位，伴随着流向涡能的不断耗散，拉伸项在对数层起到了关键作用，导致流向涡强度随时间演化得到了增强。

致 谢

感谢中国科学院力学研究所李新亮团队提供计算程序帮助，国家超级计算广州中心为课题开展提供运行平台。