用动态画板实现超声波反射、折射和波形转换的动态演示

徐平军

【摘  要】通过应用GeoGebra动态画板演示了超声波的反射、折射和波形转换的动态演示，设置了钢轨超声波探伤中常用的探头入射角、介质声速等参数，生动直观地展示了这些参数对反射、折射、波形转换的影响。

【关键词】钢轨超声波探伤;反射;折射;波形转换;动态画板;GeoGebra

1 简介

无损检测是钢轨探伤工的基础课，超声波的反射、折射和波形转换是其中难点之一，其原理复杂、抽象、理论性强，我们新职工在学习中往往不容易掌握，本文以超声波平面波为例，通过GeoGebra的动态演示了平面波在平面、曲面上的各种状态，将抽象的理论变得形象，将笼统的知识点变得直观，帮助学员能很好地掌握知识点。

2 超声波在平面上反射过程

2.1 反射的定义：超声波从一种介质传播到另一种介质时，在两种介质的分界面上，部分能量反射回原介质内，这种现象称为反射。界面上这种声能（声压、声强）的分配和传播方向的变化都遵循一定的规律。

2.2 操作过程

（1）如图1为一入射纵波经CO入射至AD界面上，形成OC₁的反射纵波。假设入射角为α1，纵波反射角为γ_L，第一介质纵波声速为C_L，根据折射定律sinα1/C_L=sinγ_L/C_L，γ_L=sin^-1（C_Lsin（α1）/ C_L）。

（2）在x-y坐标系中，如图2选择描点工具建立原点O，在x轴上建立A、D点，做直线AD表示界面，在y轴上建立B、C点，经B、C点做一条法线。如图3建立滑动条α1，类型为角度，最小值为0°，最大值为90°，增量为0.1°。

（3）如图4选择轴对称的旋转功能绘制一个以O为旋转中心，以C为对象旋转了α1的点C，做线段CO代表入射波，标示∠COC为入射角α。选择旋转工具，以O为旋转中心，以C为对象旋转了sin^-1（C_Lsin（α1）/ C_L）的点C₁，标示∠CO C1为反射角γ_L，做射线O C1代表反射纵波。

（3）如图5选择旋转工具，以O为旋转中心，以C为对象旋转了sin^-1（C_Ssin（α1）/ C_L）的点C₂，标示∠CO C2为反射角γ_S，做射线O C2代表反射横波。

（4）横波入射时过程类似，不再赘述。

（5）拉动滑动条α1，使入射角α在0°-90°之间变化，入射波和反射波也会随之变化。

3 超声波在平面上的折射过程

3.1 折射的定义：超声波从一种介质传播到另一种介质时，在两种介质的分界面上，有有部分能力透过界面进入另一种介质，这种现象称为折射。界面上这种声能（声压、声强）的分配和传播方向的变化都遵循一定的规律。

3.2 操作过程

（1）如图6为一入射纵波经CO入射至AD界面上，形成OC₃的反射纵波和OC₄折射横波。假设纵波折射角为β_L，横波折射角为β_S，第二介质纵波声速为C_L2，第二介质纵波声速为C_S2，根据折射定律sinα1/C_L=sinβ_L/ C_L2=sinβ_S/ C_S2，β_L=sin^-1（C_L2 sin（α1）/ C_L），β_S=sin^-1（C_S2 sin（α1）/ C_L）。

（2）前面步骤参考2.2。如图7选择轴对称的旋转功能绘制一个以O为旋转中心，以C为对象旋转了角度为β_L的点C₃，标示∠BO C₃为纵波折射角β_L，做射线O C₃代表折射纵波。

（3）如图8选择旋转工具，以O为旋转中心，以C为对象旋转了角度为β_S的点C₄，标示∠BO C₄为横波折射角β_S，做射线O C₄代表折射横波。

（4）横波入射时过程类似，要注意的是需合理设置第二介质中的声速，必须使得sin值在-1至1之间，否则将不会产生折射波，详细过程不再赘述。

（5）拉動滑动条α1，使入射角α在0°-90°之间变化，入射波和折射波也会随之变化。

4 超声波倾斜入射至异质平界面时产生的临界角

临界角是特殊的入射角，在钢轨超声波探伤中具有很重要的意义。

4.1 临界角的概念：当C_L2 > C_L1，则β_L=90°时对应的纵波入射角称为第一临界角，用α_Ⅰ表示。若C_S2 > C_L1，则β_S= 90°时对应的纵波入射角称为第二临界角，用α_Ⅱ表示。当γ_L= 90°时，对应的横波入射角称为第三临界角，用α_Ⅲ表示。表1为钢轨探伤中常用的临界角。第一介质中的纵波入射角α_L<α_Ⅰ，则第二介质中既存在折射横波，又存在折射纵波，如图9所示。若α_L=α_Ⅰ～α_Ⅱ，则第二介质中只存在折射横波，不存在折射纵波。当第一介质为固体时，横波入射时，若α_S≥α_Ⅲ才会有第三临界角，此时第一介质中只有反射横波，没有反射纵波。钢轨探伤中37?探头检测轨底横向裂纹具有非常好的检测效果，就是因为横波入射角α_S≥α_Ⅲ的缘故，此时反射横波很强，且与裂纹的长度无关。

4.2 操作过程

（1）前面步骤参考3.2。假设纵波折射角为β_L，横波折射角为β_S，第一介质为有机玻璃纵波声速为2730m/s，第二介质为钢，纵波声速为5900m/s，横波声速为3230m/s。建立3个按钮，标题分别是第一临界角、第二临界角、第三临界角。根据折射定律可得α_Ⅰ=sin^-1（2730/5900 sin（α1））=27.6°，α_Ⅱ=sin^-1（2730/3230 sin（α1））=57.7°，α_Ⅲ=sin^-1（3230/5900 sin（α1））=33.2°。

（2）調到第一临界角按钮的设置界面，在脚本里输入C_L=2730m/s，C_L2=5900m/s，CS2=3230m/s，α1=27.6°。第二临界角按钮的脚本中输入相同内容，并把α1改为57.7°。

（3）由于第三临界角是固体介质中横波入射的情况，所以需要增加新的参数设置，并增加反射路径，过程可参考3.2。调到第三临界角按钮的设置界面，在脚本里输入C_L=3230m/s，C_L=5900m/s，C_S=3230m/s，α1=33.2°。

（4）点击3个按钮就能直接观察到临界角的对折射波或反射波的影响。

5 超声波在弯曲界面上的反射和折射过程

5.1 当超声波入射到弯曲界面上时，其反射波将发生聚集或反射，如图4、5所示。波束与曲面上各入射点的法线成不同的夹角，入射角为0的声束沿原方向返回，其余声束的反射则随着距声轴距离的增大，反射角逐渐增大。曲面的凹凸按从发射方向看进行区分，当曲面为凹面时，反射波发生聚焦;曲面为凸面时，反射波向四周发散。

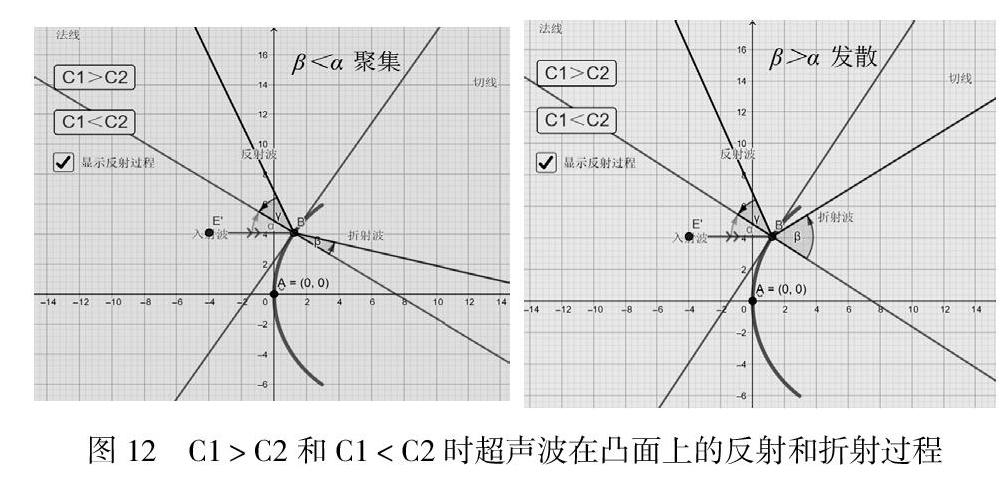
5.2 平面波入射于球面上产生球面反射波，在柱面上则产生柱面反射波，其反射声压可根据焦距f进行计算。当超声波入射至弯曲界面上使，其折射波同样会发生聚集和发散，图11、12所示是以钢/水为例说明了四种情况。

5.3 操作过程参考2.2。

6结语

本文采用GeoGebra对超声波的反射、折射和波形转换进行了动态绘图演示，同时设置了入射角、声速、临界角等参数，使学员能够直观的观察反射、折射及波形转换的过程，使得原来复杂抽象的理论知识变得生动形象，促进了他们对超声波理论知识的理解和掌握。

参考文献：

[1]铁路职工岗位培训教材编审委员会.钢轨探伤工.北京：中国铁道出版社，2014.

[2]王洪涛 石礼伟 李艳.用GeoGebra实现反射折射及双折射的惠更斯原理绘图.物理教师，2019，40（5）：75-77.