编组站作业优化研究

娄正良

（北京全路通信信号研究设计院集团有限公司，北京 100070）

0 引言

编组站主要办理货物列车的到达、解体、集结、编组、发车等技术作业，中转、装卸等货运业务以及部分客车的到达、出发等客运业务。车站行车业务主要包括接发列车作业和调车作业；在作业组织上，包括到发线运用、阶段计划编制、调车作业计划编制、进路准备等内容。

编组站作业是多工种、多单位协调合作的作业，所有作业都需要预先有计划［1］。目前编组站的计划种类有班计划、阶段计划、调车运用计划、本务机接续计划。所有这些计划都是远期的（3～4 h），对实际作业有指导作用，然而并不能直接用于实际作业，在实际作业中，还需要值班员和调度员根据站场场景灵活决定每个作业使用的进路、调车、作业次序和方式。这种作业完全依赖作业人员现场发挥的特点正是目前计划体系的不足。

娄正良［2］研究与机车走行关联的局部作业优化方式；史峰等在到发线运用方案确定的前提下，从不同角度研究进路排列优化问题［3-5］；陈彦等对列车占用到发线和道岔进行相容性约束，以减少约束条件［6-7］；其中文献[6]设计模拟退火算法在极大可行解范围内搜索，大幅缩小了求解范围；乔瑞军等针对客运专线列车运行图编制阶段的到发线运用问题，构建多目标优化模型，提出基于目标协调优化思想的求解方法，求得到发线运用方案可以使列车站内走行时间最少、到发线使用更均衡，从而使车站接发车作业效率更高，但没有考虑到接发车进路有多条选择时，如何将进路选择与到发线运用协调优化问题［8-9］；朱亮等［10］将到发线运用与进路选择作为一个多层次约束条件动态规划问题，根据运营要求约束、到发线功能约束、后效性约束和优化条件约束，逐步缩小搜索范围，得到局部最优解，但此模型基于动车组假设，不能应用于普通列车，并且不适用于上下行站场连通的情况。

在给定编组站站型结构和阶段计划确定的前提下，充分高效地利用站内设备，完成货物列车运输组织。在进路与到发线资源不相扰，并且满足到发线使用偏好的约束条件下，以车站各项作业等待时间二阶距之和最小为优化目标，建立数学模型，可以较好地解决运输组织优化问题。且通过建立数学模型，利用计算机可解决模拟运输中人工模拟的繁琐和不准确问题。

1 编组站作业

1.1 作业描述

编组站作业主要有货物列车的解体和编组，本务机换挂、出入段，货物车辆的取送等业务，可作如下划分：

（1）终到列车的列车到达、技术作业、列车解体；

（2）始发列车的集结、编组、技术作业、列车出发；

（3）通过列车的列车到达、站内通过、列车出发；

（4）本务机入段、出段、立折；

（5）专用线、车辆段、机务段等车辆取送作业；

（6）车辆重复解体、取送交流。

编组站的作业基本上都是由以上各类作业交织在一起，形成错综复杂的作业网络。假定车站在一个阶段的作业都由阶段计划确定，以下并不讨论这些作业做不做，而是讨论怎么做，即关注这些作业的次序、路径、停车点的位置等。并且主要关注这些作业对资源的独占性，据此建立模型，如技术作业，主要考察对股道的占用，而不考虑作业人员的分派和占用。

为了便于计算机处理，将上述的所有作业切分成具有逻辑意义的独立作业单元，以ψ来表示1个作业单元：

式中：Ψs为ψ开始前驱作业集合，即必须等Ψs都完成后ψ才可以开始；Ψe为ψ的结束前驱作业集合，即必须等Ψe都完成后ψ才可以结束；Γ为作业类型，名称表征该作业单元的实际意义，在系统中用于打印和输出；V为作业单元的作业序列，该作业序列中的元素称为作业节点υi，每个作业序列节点可以用1个四元组来表示。

式中：tsi为作业节点的开始时间；tei为作业节点的结束时间；ri为作业路径资源，可以认为是1 组进路的组合；ξj为需要独占的资源，在编组站内是指调车，但对于解体钩计划，并且采用双推单溜的编组站，独占资源还包括驼峰资源。

作业单元拆成1 个作业序列，该作业序列有2 个特殊的作业节点，分别是开始作业节点υ0和结束节点υn+1。υ0为该作业单元可以开始的标记，受制于Ψs，如果没有限制，那么可以取一个合适的值，如班计划开始时间，从后面的模型中看出，对于没有限制开始的节点，取值对结果影响很小。作业节点υn+1为作业单元结束的标记，受制于Ψe。这2个特殊节点的ri和ξi为空，即ri=φ。作业单元中的作业节点必须顺序执行，每个作业节点一旦开始，就必须一次性执行完，即作业节点是作业执行中的不能拆分的原子操作。1个单元作业过程示意见图1。

图1 1个单元作业过程示意图

车站的所有作业都可以使用上述作业单元所述模式来表达，那么编组站所有的作业可表示为：

式中：ΨE为编组站所有的作业，假定可以分割成m个作业单元。这些作业单元之间内在的联系是依靠每个作业单元的开始前驱作业集合Ψs和结束前驱作业集合Ψe来表达。编组站的这种内在关系主要是由现车和调车等引起的，为了降低模型的复杂性，将现车分配作为由阶段计划确定的已知因素，而不作为模型的变量。若扩展模型，将现车作为模型的变量，就可用以优化编制钩计划。

以编组站的入段、解体、编组为例来说明上述的模型描述：

（1）入段作业比较简单，可以作为1个作业单元处理，该作业单元的开始前驱作业集合是接车作业单元，入段作业通常不是一次性完成的，入段的过程中可以在某个区段停留下来，为别的作业让道，那么可以将整个入段路径上所有可以停车的地方表示出来，以这些停车点将入段路径分割成1个作业序列，形成入段作业单元的作业节点集合。入段径路不需要调车，因此其ξj为空。

（2）解体作业比较复杂，可以分为预推和推峰2个部分，因此1 个单纯的解体作业可以划分为2 个作业单元，而预推是一次性完成，中间没有停顿，因此预推作业单元的作业节点有3 个，分别是预推开始，预推，预推结束。而解体作业的钩计划比较复杂，有的解体有30 多钩，但可以将解体计划视作1 个作业单元，解体动作一旦开始，中间不能停顿，而且独占驼峰资源（双推单溜），因此同样解体作业单元也包括3 个节点，分别是解体开始、解体、解体结束3个作业节点。

（3）对于平面调车的钩计划，如编组，通常每一勾都是1个作业单元，在调车运行过程中，空程时可以随时停车，而带车则须一次性走完整条路径，因此带车的作业节点较少，而空程的作业节点较多。

1.2 决策内容

建立模型主要解决以下决策内容：

（1）作业单元的次序。

（2）作业节点的节奏。每个作业单元可能不是一次性完成的，如本务机入段，可能走走停停以避开相扰（让行其他调车作业和列车运行），或者等待关联作业完成。

（3）作业单元的独占资源。独占资源主要指驼峰（双推单溜）、调车、存车线等。若为了降低模型的复杂度和搜索规模，也可去掉其中的某些独占资源决策，而采纳阶段计划中的输入。以下假定独占资源只有调车，加入其他独占资源的处理方式与之类似。

（4）径路资源。模型中径路资源属于部分决策变量，很多作业有固定走法，如下行编组，不可能走到上行去。在作业单元中，随着独占资源、本区域前后作业确定，其径路也大体确定，选择1条干扰最小，距离最短的径路即可。模型的径路决策是指当径路必然要与其他作业造成干扰时需要对具体径路进行选择。选择不同径路，造成的干扰范围、干扰程度不同，进而模型计算出的目标值不同。

2 数学模型

2.1 作业时间

编组站多数作业是有先后次序的，但是也有很多作业是可以平行作业的，在实际工作中也会尽量创造平行作业机会以提高作业效率。数学模型建立的单元作业首先要满足时间要求。

（1）由于作业节点需要一次性执行完，因此tei是仅依赖于tsi的变量：

式中：c(ri，Γ)为常量，其值随着作业类型和径路确定，属于字典类数据，以下将其定义为受作业类型和径路等字典类数据影响的变量。

（2）在1个作业单元内部，作业序列是严格按照顺序来执行的，因此需要满足如下关系：

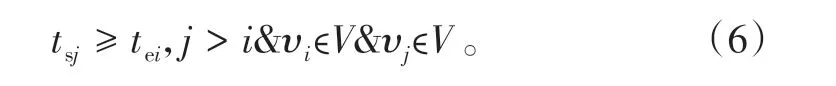
（3）任意1个作业单元ψ的开始和结束节点需要满足其前驱作业集合的限制：

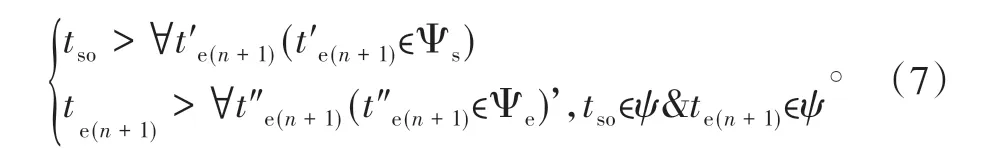
2.2 作业径路

作业径路是整个模型重要决策变量。很多作业执行次序、执行方式的改变都是因为作业径路的干扰。以下作业径路不仅指路径，还包括股道，如技术作业，其作业径路就是列车的停留股道。

作业径路是一种独占资源，因此要求所有的径路都不能相扰，否则必须通过时间错开达到不相扰。

为了不失一般性，假设任意2 个作业单元ψm和ψn的任意2个作业节点υmi和υnj为：

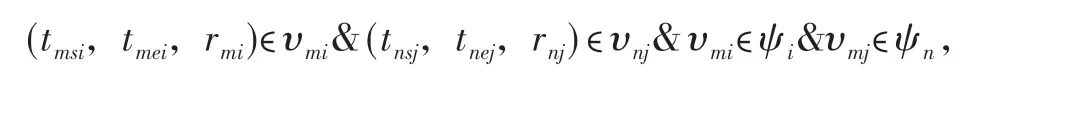
如果时间上存在重叠，即：

那么，径路上就不能相扰：

2.3 独占资源

作业单元中需要使用独占资源，调车作业的独占资源是机车，驼峰解体的独占资源还包括驼峰（双推单溜），接发列车和本务机作业单元没有独占资源。独占资源的限制和作业径路类似，其实作业径路也是一种独占资源。

为了不失一般性，假设任意2 个作业单元ψm和ψn的任意2个作业节点υmi和υnj为：

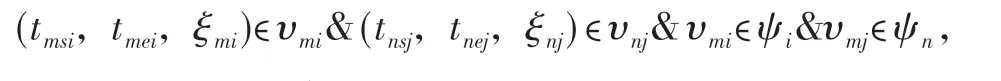
如果时间上存在重叠：

那么对于独占资源ξmi和ξnj就不能相扰：

2.4 模拟运输目标

编组站的模拟运输目标是充分高效地利用站内设备，完成车站各项作业。上述目标很难量化，也无法将上述目标作为模型的目标。因此，从作业的角度来考察模拟运输的效率，制定数学模型的目标是均衡、紧凑地完成车站各项作业。

首先以接车和发车为参照，为车站的每个作业制定1个作业时间的参照，以到解列车为例，接车作业单元的开始时间就是计划接车时间，而解体的开始时间就是接车时间加上技术作业时间，也就是解体最早可能开始的时间。然后根据作业时间与参照时间的差值来计算作业方案的优劣。

（1）对于1 个作业单元ψm，其作业节点中开始节点υ0表示这单作业可以开始的时间，实际上是最早开始时间。如果该作业从能够开始的时候就进行，并且一直到结束，中间没有延误，那么认为该作业是最理想的作业方式。

1个作业单元延误的时间就是这个作业单元每个作业节点的延误时间：

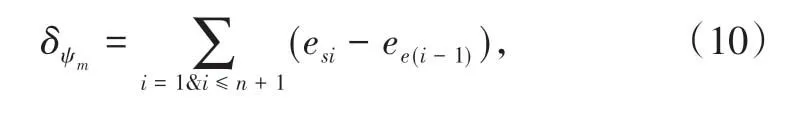
那么所有作业单元的延误时间：

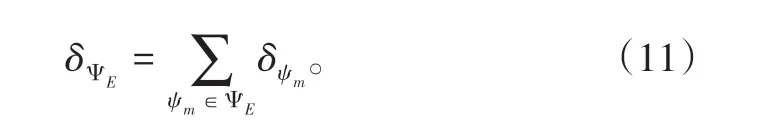
在实际作业中，每个作业由于其他作业的影响，都或多或少有些延误，而考察作业效率的高低，可以考察作业的延误时间。如果车站只进行1个作业，那么无论怎么安排计划，都不会延误，即无论如何做，效率都是最高的，而如果有很多计划交织在一起，那么组织这些作业的方式、次序对效率影响很大。

上式中，所有作业对延误时间δΨE的“贡献”都是相同的，但用户可能会认为一些作业重要，一些作业不重要，因此定义一个权值，仅和作业类型相关的常量，表示为ω(Γ)，那么上式改为：

（2）模拟运输目标是尽可能减少整个作业的延误时间，也就是紧凑目标，但这样会出现某项作业延误很长时间，而其余作业延误时间较短的情况。因此δΨE反映了整个作业的紧凑度，还不能反映整个作业的均衡度。

修改上述的作业的δΨE，改用每个作业单元的延误时间二阶距ΔΨE作为衡量整个作业的均衡、紧凑的指标。

通过对编组站的所有作业建立数学模型，将模拟运输的优化转为通过计算机的手段来寻找最优指标的ΔΨE搜索过程。

2.5 数学模型

根据以上对目标和约束的讨论，建立编组站作业组织优化运输模型为：

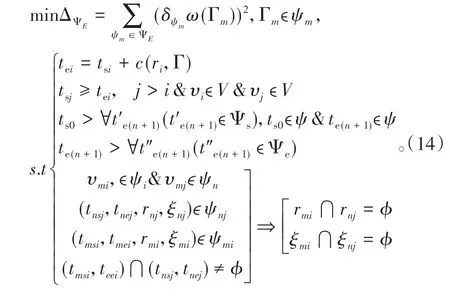
将车站作业抽象成模型描述的方式，在满足约束条件下寻找最小的ΔΨE，在最小的ΔΨE下，编组站作业方式是最小的，是最紧凑、均衡的组织方式，同时也是在既有作业量下，设备利用效率最高的方式。

2.6 模型求解讨论

2.6.1 建立模型

按照上述编组站业务描述，将阶段计划内所有即将进行的作业抽象为作业单元的集合ΨE，然后根据计划类型和现车关系，设置为每个作业单元的Ψs和Ψe。计算每个作业单元的开始节点时间和结束节点时间。

2.6.2 设定常量

模型中有2类常量需在模型求解前预先设定：

（1）作业节点执行时间c(ri，Γ)。作业节点的开始节点和结束节点只是一个标记，其执行时间为0，即ts0=te0和ts(n+1)=te(n+1)，而其余节点的执行时间主要和路径的长度有关系，所以需要对站场进行测绘。根据每个设备的长度，以及路径经由的设备，计算路径长度，由作业类型设定其运行速度曲线，并计算作业节点执行时间。

（2）延误时间权值ω(Γm)。延误时间权值用于表示作业重要程度，如编组站的非重要作业（站修线取车等）的作业权重可以小一点。延误时间权值是主观性比较强的参数，需要参考车站作业人员的意见，也可用于模型输出的调整。

对于那些没有明确开始时间的作业，延误时间权值可以定得小一点，开始时间则可定义得早一点。

2.6.3 最优解

公式（14）编组站作业模型是个典型的完全多项式非确定问题（NPC），即模型的解需要去尝试和猜测，但每个解都可以很容易地去求解其模型目标值，然后依据目标值判断解的好坏。以下仅讨论采用穷举法，将满足约束的所有可能解一一枚举出来。采用式（8）计算每个解对应的紧凑、均衡度，并选出最优解。

2.6.4 解空间

根据式（2），每个作业单元ψ的作业节点的个数记做|ψ|，而对于所有的作业单元ΨE，其含有的所有作业节点数为|ΨE|：

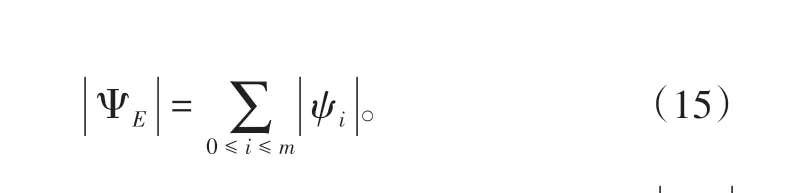
那么，作业节点的全排序的解空间为Ω 就是|ΨE|的阶乘，记做：

考虑到同一个作业单元内部的作业节点有序，则：

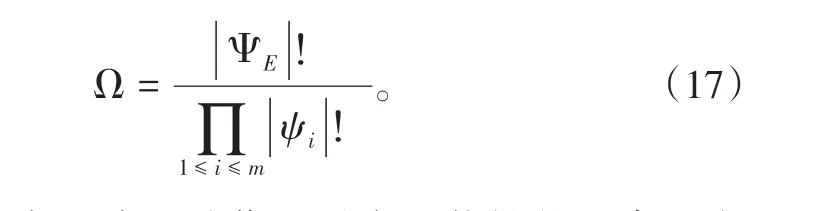
式（17）表示编组站作业最大可能性的组合，由于作业开始和作业结束约束、调车约束、站形约束等会大大降低解空间的规模。以下讨论具有代表性的机车资源对解空间的影响。

假定编组站内有u台调车，那么这些作业单元根据所使用调车分割成u+1 个集合。其中每台调车对应1 个作业单元集合ΨLi，把不需要调车的所有作业单元合并到1 个集合ΨL(u+1)。假定ΨL(u+1)单元作业的个数是m′，则解空间为：

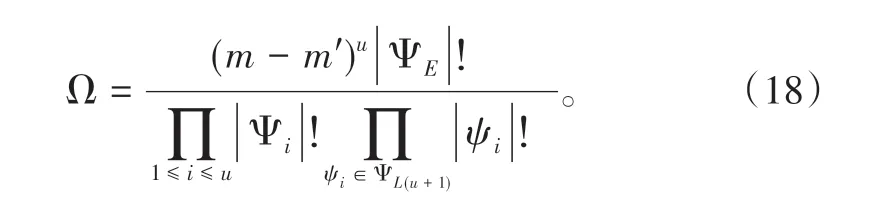
2.6.5 求解模型

采用穷举法，通过剪枝、降低问题规模等来达到快速求解的目的。

（1）划分子集。编组站很多作业单元可以根据作业区域和作业时间来划分成互不关联的作业集合，如在车站1个班内，到达列车有密集到达的，也有空闲到达的，这样有可能在时间上将ΨE分成几个集合；同时有些作业在解体区域，有些作业在编组区域，也可以划分成不同的集合。假定可以划分成μ个结合。那么可以将解空间降为：

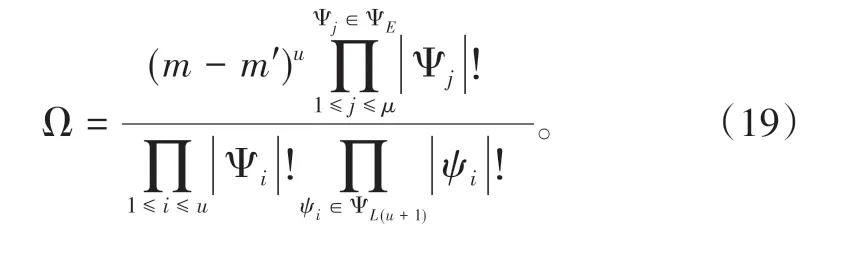
（2）剪枝。在搜索的过程中，可以随时抛弃明显不合理的解，即剪枝。在实际应用中，剪枝对搜索速度的影响极大。剪枝的权值设定可以根据经验设定，也可以估算。由于只需要搜索模型的1个最优解，如果估算权值越接近最优解的权值，则剪枝的效果就越明显。

如果估算目标值，则首先假定平均每个作业单元延时30 min，然后根据平均值计算模型的目标值ΔΨω。在搜索的过程，随时检查最优解的目标值，如果超过ΔΨω，则直接剪掉。估算的目标值对搜索范围影响很大，通常可以尝试定一个比较优的目标值，如果搜不到解，则逐步放开目标值。目标估计值设定流程见图2。

（3）缩小问题规模。模型的解空间随着作业节点的个数成指数级地增长，因此为了提高搜索最优解的速度，可以减少作业节点个数。在工程实际应用中，通过减少求解问题的时间宽度解决，即只对最近1 h 的编组站作业进行优化求解。

图2 目标估计值设定流程

整个模型求解过程见图3。

图3 模型求解过程

3 实验验证

编组站作业组织优化是一个很难定量分析的值，对于1 个车站，每天的作业都在变化，即使同样的作业，不同作业人员的作业方式也不同。主要通过兑现率和模型目标函数值（均衡紧凑度）2个指标评价模型的优劣。选择某车站4 月份3 个日班，上午、下午、晚上各1 个时间段作为验证时间。选择的标准是：3 个时间段的作业比较有普遍性，没有交班、施工等异常情况的干扰，且作业比较饱满。

兑现率是指模型决策内容与车站实际作业情况进行比较的结果。从模型中求解出来的作业，如果其作业单元次序、作业节奏、独占资源、走行径路等和实际作业一致，则认为该作业兑现了。兑现率反映模型的最优解与实际作业过程的贴合度。选择模型验证时间的兑现率见表1。

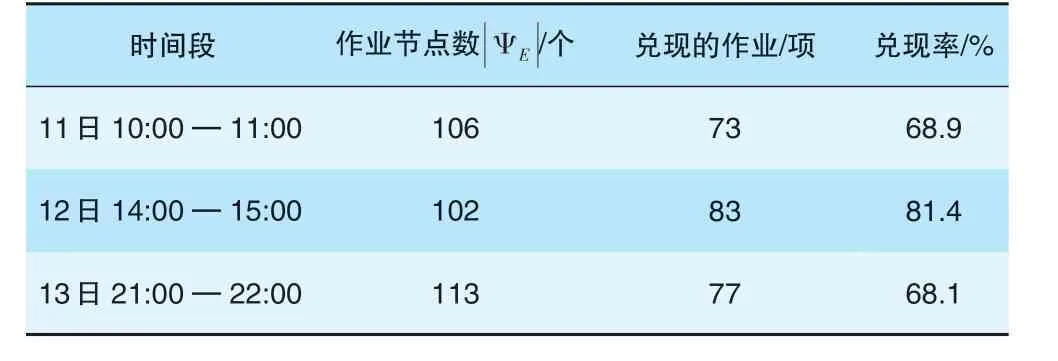
表1 验证时间的兑现率

模型计算出的这些作业节点的均衡、紧凑度之和见表2。

表2 作业节点均衡紧凑度之和

从上述的数据可以看出，模型产生的作业序列兑现率是72.6%，而从均衡、紧凑度上看，模型所安排的作业组织明显优于车站的实际作业组织。由此可见，车站的作业组织还有优化空间。

4 结束语

建立的编组站作业组织优化运输模拟推演模型综合考虑了到发线路，接发车进路，单机转移、调车、出入段、立折、转头等编组站所有的作业，并对这些作业的作业次序、作业所使用资源进行了优化。模型贴近于实际作业，具有很高的实用性。从实验结果可以看出，模型较好地拟合现场作业，其作业的均衡度和紧凑度都明显优于实际现场作业。