碳排放影响因素以及脱钩分析研究综述
王天庆 王晓辉 彭书传
(1. 合肥工业大学资源与环境工程学院,安徽合肥 230009;2. 安徽省环境科学研究院,安徽合肥 230061)
1 引言
人类不断开发运用能源和自然资源,导致二氧化碳(CO2)的排放量大幅增高,引起了温室效应等全球性环境问题,阻碍人类社会的可持续发展。作为负责任的大国,我国承诺:相较于2005 年,2020 年和2030 年我国的单位GDP 二氧化碳排放将分别下降40%~45%和60%~65%。我国目前减排压力较大,为实现减排目标,了解影响碳排放的驱动因素以及碳排放与经济发展的联系是很有必要的,本文就此对目前常用的研究方法进行了归纳概述。
2 碳排放数据来源
进行碳排放研究首先需要解决的问题就是碳排放数据的核算,但是我国目前没有进行对碳排放量的直接监测,因此需要借助碳排放量核算方法模型来得到研究所需的碳排放量。目前的研究中,CO2排放总量数据来源通常是参照2006 年IPCC(联合国政府间气候变化专门委员会)公布的国家温室气体清单指南中关于污染物的排放系数的计算方法计算得到,即与化石能源相关的CO2排放量等于活动数据乘以排放系数。计算公式为:
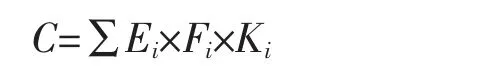
式中,C 表示碳排放总量;Ei表示第i 类能源消费量;Fi表示第i 类能源折算标准煤系数;Ki表示第i 类能源碳排放系数。
其中,能源类型一般为原煤、汽油、煤油、柴油、天然气、燃料油、电力、原油等,具体研究中也可根据研究对象的实际情况灵活选取。化石能源消费量可以通过《中国能源统计年鉴》中相应的实物量能源平衡表获得,碳排量系数和折算标准煤系数也基本来自中国本地化的碳排放参数。
3 碳排放影响因素研究
研究碳排放影响因素的方法较多,本文介绍目前使用最为广泛的2 种方法:对数平均迪氏指数法(Logarithmic Mean Divisia Index,即LMDI)和可拓展的随机性的环境影响评估模型(Stochastic Impacts by Regression on Population,Affluence,and Technology,即STIRPAT)。
3.1 LMDI 法
LMDI 法属于指数分解方法的类别,即通过将目标变量的变化分解为若干驱动因素的组合,进而根据各因素的数据判断它们的影响程度。Kaya[1]在1989 年IPCC 的一次研讨会上提出了碳排放的Kaya恒等式,将碳排放的驱动因素分解为单位能耗的CO2排放、能源强度、人均GDP 和人口。表达式如下:
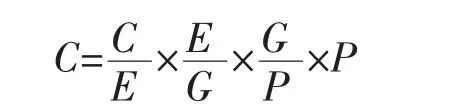
式中,C 表示碳排放量;E 表示能源消耗量;G 表示GDP;P 表示人口。LMDI 法通过扩展Kaya 恒等式将CO2排放总量按各个影响因素进行分解,进而分析各因素对CO2排放总量的驱动作用。具体的影响因素可以根据研究对象的不同进行灵活选取,采用适用于研究对象的影响因素。分解方法分为2 种:乘法分解是将基期和报告期的碳排放之比表示为各影响因素相对贡献的乘积;加法分解则是分解碳排放量在一个时期内绝对数的变化,分解出各影响因素变化导致的碳排放增量。
LMDI 分解法可以有效避免残差项和数据零值,且结果明了,易于解释,被广泛应用于各区域、各领域对碳排放因素的分解研究中。李颖[2-3]通过LMDI法研究了安徽省农村居民生活消费碳排放的影响因素、安徽省交通运输业碳排放影响因素等;安芬等[4]通过LMDI 法研究了贵州生活能源碳排放影响因素;郑颖等[5]通过LMDI 法研究比较了我国典型城市化石能源消费CO2排放及其影响因素。
3.2 STIRPAT 模型
美国生态学家Ehrlich 和Holdren[6]于20 世纪70 年代提出了IPAT 模型(即I=P×A×T),表明了环境压力(I)与人口规模(P)、富裕程度(A)、技术水平(T)的联系,但由于该模型是恒等式模型,假设没有随机因素的情况下,各个影响因素对于环境压力之间的关系都是等比例的关系,而现实中各影响因素大多非单调且不成线性关系。Dietz 等[7]为了克服这个局限性,将IPAT 重新构建为一个随机模型,对影响因素加上了随机影响,称为STIRPAT 模型。表达式如下:

式中,I 表示环境压力;a 表示模型系数;P 表示人口规模;A 表示富裕程度;T 表示技术水平;e 表示残差项;b,c,d 分别表示各影响因素的指数。后York 等[8]指出STIRPAT 模型中所有变量均为对数的形式更便于估计和假设检验。将模型进行对数化处理后变换为lnI=lna+blnP+clnA+dlnT+lne。基于此等式,结合数据就可以分析人口规模、富裕程度、技术水平对环境压力的影响程度。显然,模型中的环境压力可以是碳排放量,即此模型可以用来研究碳排放的影响因素。
同时,还可以针对研究的具体情况对STIRPAT模型中的因素进行增减或分解。例如,闫树熙等[9]在《交通碳排放影响因素分析——以西安市为例》中使用STIRPAT 模型分析西安市交通碳排放影响因素时,把富裕程度扩展为人均GDP、客运周转量和货物周转量因素,把技术水平和随机因素扩展为城市公共运营车辆、地铁客运量以及单位GDP 能耗因素。再基于扩展后的模型进行分析得到相关结论。
目前,STIRPAT 模型被广泛运用于各区域、各行业碳排放影响因素研究。孙义等[10]基于STIRPAT 模型研究了黑龙江省碳排放影响因素;钱姗姗[11]基于STIRPAT 模型研究了民族地区CO2排放的影响因素;唐晓灵等[12]基于STIRPAT 模型分析了上海市和西安市的碳排放差异性等。
4 碳排放与经济水平关系研究
在分析碳排放与经济水平关系的研究当中,脱钩理论被广泛运用。“脱钩”的概念自20 世纪60 年代被提出后逐步扩展到了环境经济学等研究领域,通常用来描述环境污染与经济增长之间的关系,具体体现为脱钩指标的度量,即通过脱钩指数来体现环境污染与经济发展联系的紧密程度。该理论主要有2 种脱钩模型:OECD 脱钩模型和Tapio 脱钩模型。其中,OECD 脱钩模型利用环境压力与GDP 比率的期末值和期初值之比表征脱钩状态,可以有效判断经济发展与环境污染的相联关系,但无法区分不同的脱钩状态。2005 年Tapio 建立了Tapio 脱钩模型[13]。该指数在基期选择上不敏感,同时还具有较强的脱钩状态识别能力。
Tapio 脱钩指数以时期为时间尺度反映变量间的脱钩关系。以碳排放为例,其脱钩指数是以研究期初和期末间碳排放与产值的变化率之比进行表征,如下式所示:
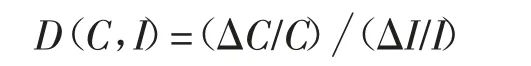
式中,D(C,I)为某一时期内碳排放的脱钩指数,C 表示基期碳排放量;I 表示基期产值;ΔC 表示目标期相比基期碳排放的变化量;ΔI 表示目标期相比基期产值的变化量;ΔC/C 表示目标期相比基期碳排放量的变化率;ΔI/I 表示目标期相比基期产值的变化率。依据D(C,I),ΔC,ΔI 的不同数值组合,可划分为强脱钩、弱脱钩、衰退脱钩、增长连结、衰退连结、强复钩、弱复钩、扩张复钩8 种不同的脱钩状态。通过不同的脱钩状态与实际情况结合可分析得出研究结果。
Tapio 脱钩模型在各地区、各行业分析碳排放与经济水平关系的研究中得到广泛运用。近期的研究中,杨庆等[14]对安徽省碳排放进行了脱钩效应分析;韩亚芬等[15]分析了安徽省工业行业碳排放的脱钩效应及驱动类型;曹庆仁等[16]对北京市居民消费支出与碳排放的脱钩关系进行了分析;王越等[17]对东北三省的碳排放脱钩效应进行了研究;胡莉娜等[18]基于脱钩理论对西藏旅游业碳排放与经济增长关系进行了研究;王杰等[19]研究了中国高耗能行业碳排放脱钩关系等。
5 综合分析研究
在碳排放的影响因素以及脱钩关系研究中,有学者将两者结合起来,研究了经济增长与碳排放脱钩关系的影响因素。如孙叶飞等[20]将Kaya 恒等式进行了扩展得到了能源消费碳排放与经济增长的脱钩模型,结合碳排放数据将每种因素对脱钩指数的影响进行了定量分析,从时间和空间的角度上对中国能源消费碳排放与经济增长脱钩特征及驱动因素进行了全面的分析;魏营等[21]基于Tapio 脱钩理论和LMDI 分解技术构建了脱钩因素分解模型,对镇江市的重点碳排放工业行业的碳排放脱钩效应进行了因素分解;刘丽娜等[22]剔除了经济因素对农业碳排放的影响,构建了农业碳排放的脱钩努力指数模型,来权衡除了经济因素以外的其他措施对碳减排的脱钩努力的影响程度等。

