RBF神经网络结合PID控制系统优化方案及应用实现

尹亚南，韩 浩

（郑州电力高等专科学校，河南 郑州 450000）

传统控制方法要求被控制对象具备更加精准的数学模型，同时该方法仅可应用于具有反馈能力的确定性线性系统中，但随着社会生产水平的不断进步，被控制的对象结构和控制条件变得更加复杂，在大多数的控制过程中会出现具备耦合特性的多输入、多输出系统，且通常情况下会受到控制系统自身参数及结构不确定性的影响，因此建立更加精准的数学模型困难程度较大，同时传统控制方法的各项性能很难满足当前社会生产的需要[1]。PID控制系统是当前工业生产中过程控制方面最常用的一类控制设备，在应对一般生产流程时，能够表现出良好的鲁棒性，且参数整定和实践具有一定丰富的经验积累，更具备结构简单，易于操作等优势。但对于控制过程中存在非线性较强，存在较多不确定因素的系统而言，PID控制系统的使用效果并不理想。基于此，本文结合RBF神经网络对PID控制系统的优化方案进行研究，并将优化后的PID控制系统应用到实际。

1 RBF神经网络结合PID控制系统优化方案

1.1 基于RBF神经网络的PID控制系统参数优化

本文结合人工智能算法中的RBF神经网络对PID控制系统的参数进行优化，通过在RBF神经网络中学习输入的数据，对PID进行学习优化，从而得到适用于PID控制系统的优化参数[2]。在RBF神经网络中共有三层结构，其中隐层为回归层。A=[a1，a2，a3，…，an]表示为神经网络中的输入集合。具体优化方法如下：

第一步：在RBF神经网络中输入特征参数。

第二步：引入神经网络优化性能指标函数：

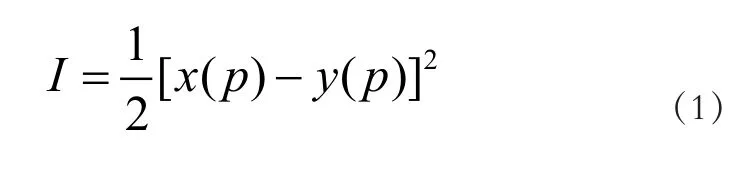
公式（1）中，I表示为神经网络优化性能指标函数；x（p）和y（p）分别表示为RBF神经网络中的输入的两个特征参数；p表示为网络的迭代步骤。

第三步：根据公式（2）进行迭代运算：

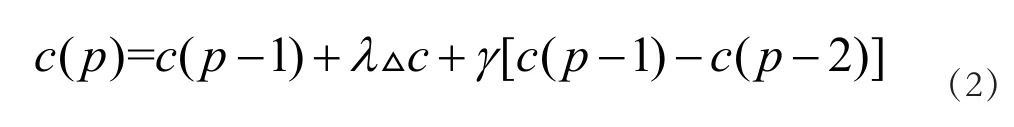
公式（2）中，c（p）表示为迭代运算结果；λ表示为惯性效应因子；γ表示为学习速率。

第四步：利用雅克比矩阵的输出结果对输入特征参数的最优线性逼近点进行优化，并推导出优化目标输出信息对变化的PID控制系统的输入信息的灵敏度。

第五步：基于RBF神经网络对数据进行分析，对PID控制系统学习的控制参数进行实时调整，从而自动实现对PID控制系统参数的调整和校正，提高控制水平[3]。

完成对PID控制系统参数优化后，利用如下公式，对其控制误差进行计算：

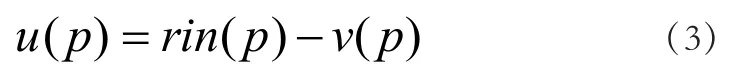
公式（3）中，u（p）表示为PID系统控制误差；v表示为PID控制系统输出数据；rin表示为输入信号。最终通过上述算法流程实现对PID控制系统参数的在线实时优化控制：

首先，设置PID控制系统控制参数到初始状态，根据RBF神经网络算法得到相应的控制参数。

其次，通过数据信息采样，计算出输入信号rin（p）和输出数据v（p），根据公式（3）计算出u（p），最后得到神经网络的输入参数。

在PID控制系统运行过程中利用RBF神经网络对网络参数进行优化，并利用相关算法得到控制系统的各项权重，并经入到第二个周期的控制中。

1.2 PID控制系统结构优化

结合RBF神经网络再对PID控制系统的整体结构进行优化，利用神经网络中的混沌寻优具备的随机性和遍历性，将处于混沌状态的参数变量引入到PID控制系统中的参数域，再利用混沌变量对全局进行粗略的搜索和采集，从而找出PID系统运行参数与RBF神经网络权系数的次优值，并将此作为基础，引入更加细致的局部搜索模式，最终找出PID控制系统的全局最优结构，图1为优化后的PID控制系统结构。

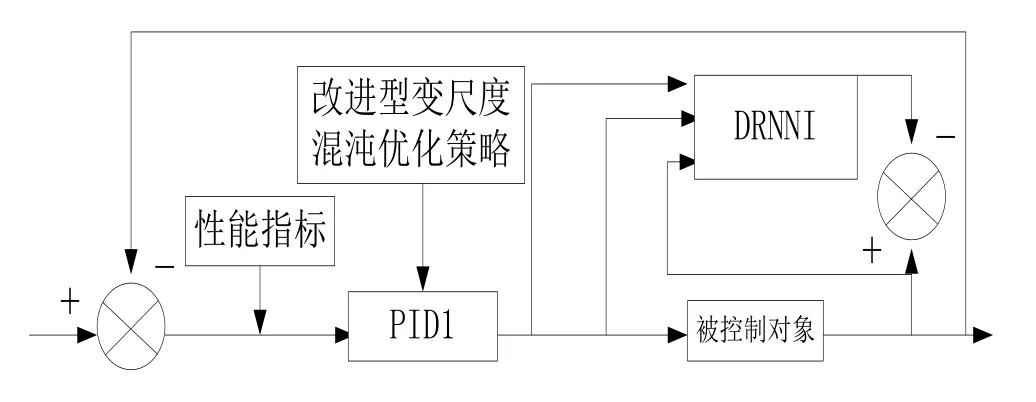
图1 优化后PID控制系统结构示意图

优化后PID控制系统结构可以在变尺度优化算法中迅速下降，并将此优势作为基础，利用并行模式搜索，提高神经网络的搜索可信度，从而将整个提供的优化效率及性能提升，进而实现对被控制对象的最优控制。

1.3 变尺度混沌策略优化

结合RBF神经网络改变原有PID控制系统的变尺度混沌策略，首先改变系统初始化参数与初始追的选择策略，假设p=0表示为混沌变量的迭代标志，B1为粗略搜索的次数，B2为细致搜索的次数，M=（p1，p2，p3，…，pn，g1，g2，g3，…，gm）表示为PID控制系统的所有控制参数集合，因此此时混沌变量的最优值变为M=（p1*，p2*，p3*…，pn*，g1*，g2*，g3*，…，gm*），则当前最优目标函数的输出值应为集合中最大的数。假设在[0，1]区间当中的任意14个相异的初值为混沌变量，则各个初始值当中选择满足pn≠10gm的关系，同时不能取作Logistic算法的不动点为0，0.15，0.85，0.5，1，（1+3）/4。

再对PID控制系统的搜索策略进行优化，利用RBF神经网络算法将混沌变量的线性关系映射到对应的变量取值区间当中，并将其视为系统搜索的初始阶段[4]。当系统多次完成搜索结果，并且结果误差满足设定的终止条件时，视为搜索结束，并将搜索结果标记为最优搜索结果。将系统搜索初始值带入到Logistic算法的映射当中，从而得到不同轨迹的混沌变量，并将其线性关系映射到设定的变量取值区间当中。利用混沌变量进行首次粗优化搜索，并计算出系统性能指标，采用ITAE目标函数准则对其记性离散处理。

最后对PID控制系统的混沌变量组成策略进行优化，利用RBF神经网络算法对系统尺度进行转换，并在当前最优点的周围进行细致搜索[5]。将神经网络混沌变量的迭代标志重新设置为0，利用全新的混沌变量在最优解的附近进行搜索。当搜索结果满足精度的要求后，完成迭代，保存当前最优值。进行并搜索，找出最多函数共同的搜索值，在集合当中选择最小的参数作为最优函数值，并提取出相应的优化变量组成混沌变量。

2 应用实现

将通过RBF神经网络结合优化后的PID控制系统应用到实际的工程当中，其主要目的是对一个具备6个加热釜的设备进行温度控制调节。该装置配备PID控制系统计算机，在上位机中安装两块板卡，其中一块作为采集卡，用于测量加热釜的温度以及加热釜的压力变化数据，另一块作为模拟输出卡，主要用于驱动可控硅，利用电热丝提供热量为各个加热釜进行加热。工程主要目的是要求加热釜在300℃～600℃之间实现线性温度控制及保温，控制精度范围在-3%～+3%。由于控制系统在补偿的过程中辨识模型是粗糙的，因此沿用传统PID控制系统很难满足工程需要，因此采用本文优化后的PID控制系统对其进行控制，表1为优化后的PID控制系统控制过程中的效果数据表。

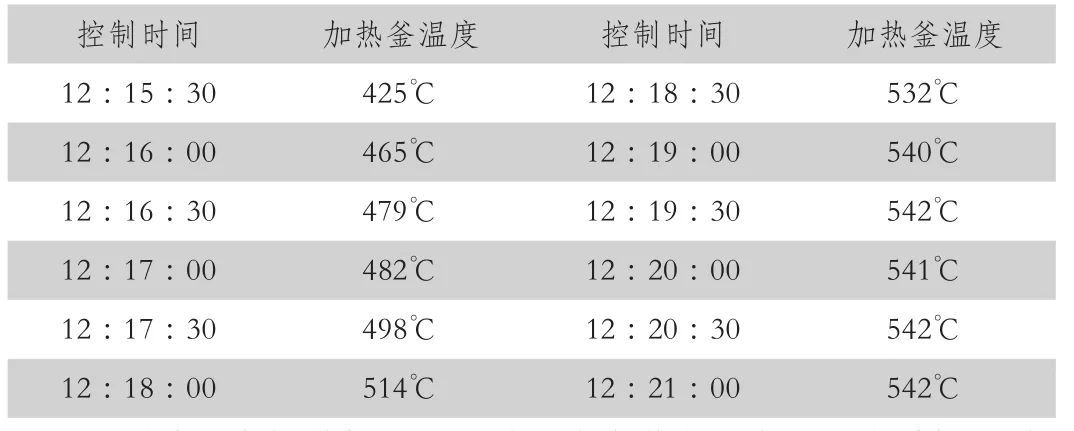
表1 优化后PID控制系统控制过程中的效果数据表

通过表1中的数据可以看出，本文优化后的PID控制系统的使用效果良好，即使是在由线性控温到保温的转化过程中，温度的偏差也得到了更好的控制，充分满足工程项目的要求。

3 结语

本文研究方向在于对RBF神经网络结合PIF控制系统优化方法的应用，目的是为了对一个未知的存在滞后时的非线性系统进行良好的控制，并从中总结出一套有效的控制策略。优化后的PID控制系统具有更高的动态响应速度和鲁棒性，且控制品质得到了大幅度的提高。