某燃气轮机压气机可转导叶IGV 流固耦合分析

罗跃飞， 吴飞， 李冠

(东方汽轮机有限公司， 四川 德阳， 618000 )

1 前言

流固耦合是研究流体与固体之间流体动力、结构弹性与惯性力之间的耦合作用, 根据作用机理分为单向流固耦合和双向流固耦合。 针对IGV流场特点, 本文采用了单向流固耦合方法, 将在流场分析中得到流体压力作为载荷加载在IGV 叶片中, 以此分析求解IGV 叶片由于流场作用所发生的形变值和应力值等。

2 IGV 流场分析

对IGV 加以流场边界条件, 气流从左侧进气,右侧出气, IGV 叶片在流场中部, 对整个流场进行网格划分, 见图1, 边界条件见图2, 这里的分析是针对60%转速工况。

图1 IGV 流场网格划分

图2 IGV 边界条件

IGV 叶片和支撑杆材料特性参数见表1, 根据《东汽金属材料手册》, 其引起0.2%残余变形的条件屈服强度在20 ℃时为760 MPa。

表1 IGV 叶片和支撑杆材料参数

流场求解后, 得到流场流线分布, 见图3～6。

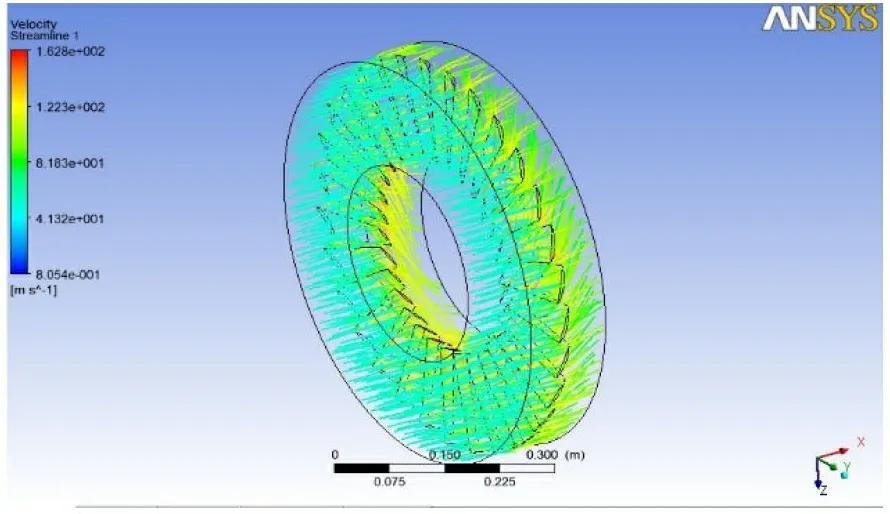
图3 流场分析结果

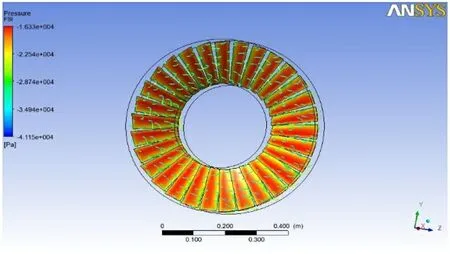
图4 IGV 叶片进气侧压力分布

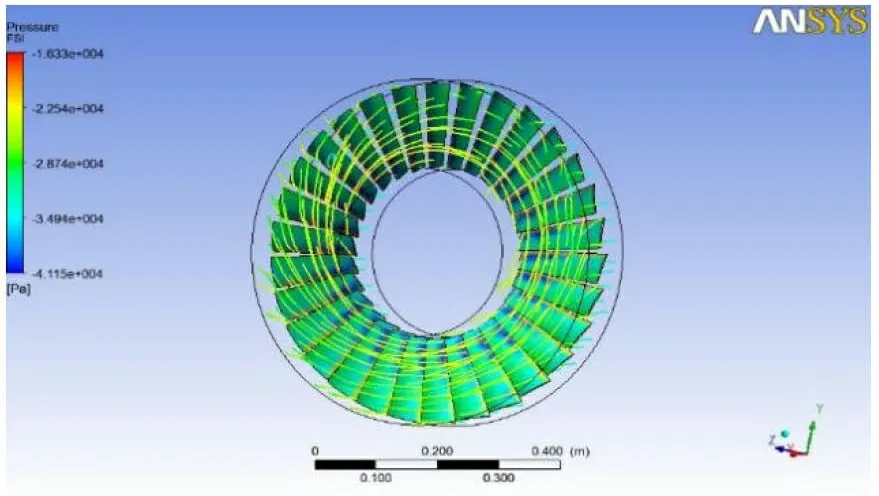
图5 IGV 叶片出气侧压力分布

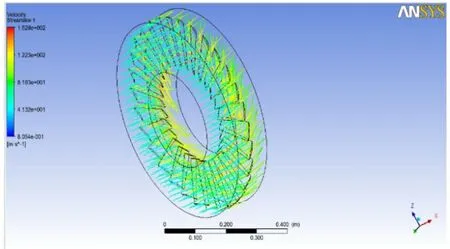
图6 IGV 流场速度分布

从图中可以看到, 流场和叶片物理分布一致,压力是呈圆周均匀分布, 此处压力是相对绝对大气压的压力, 叶片在边缘处速度大, 压力高。

3 IGV 强度分析

3.1 IGV 60%工况受力分析

将计算的流场压力导入到IGV 结构中（见图7）, 进行静力分析, 以60%工况下的转速分析计算说明IGV 结构在流场作用下形变、 应力, 支反力和支反力矩的情况, 如图8～13 和表2 所示。

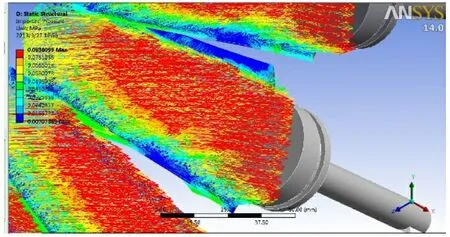
图7 流场压力导入

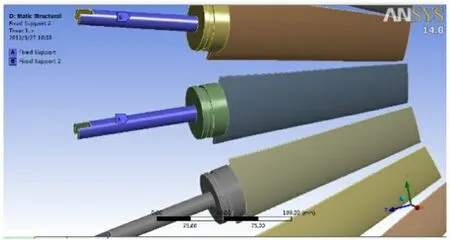
图8 IGV 叶片固定

图9 IGV 叶片整体形变

图10 IGV 叶片X 方向形变

图11 IGV 叶片Y 方向形变

图12 IGV 叶片Z 方向形变

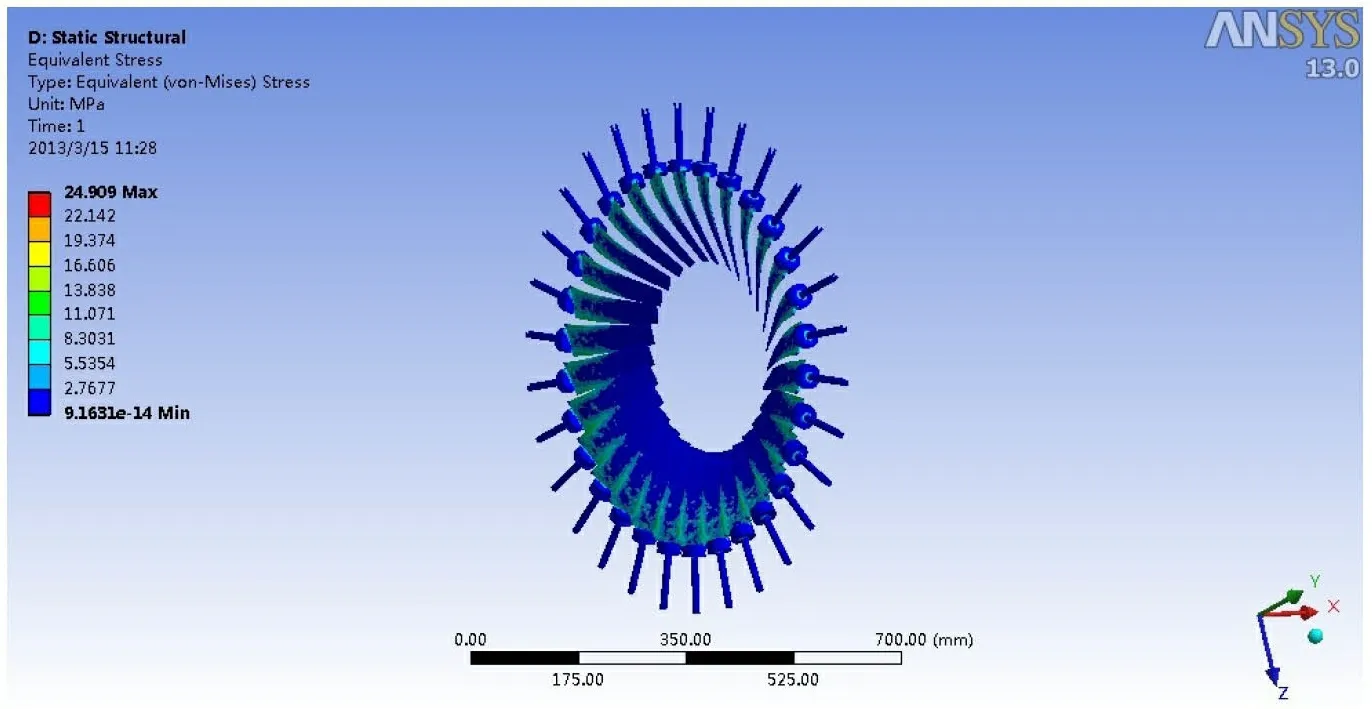
图13 IGV 叶片Mises 应力

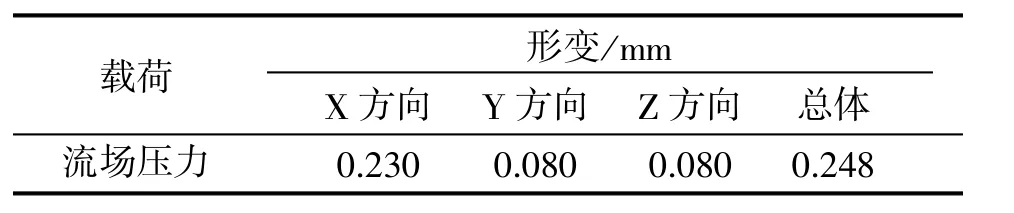
表2 IGV 结构流固耦合分析

从图9～12 和表2 可以看出, IGV 在此工况下, 叶片会发生一定形变, 最大整体形变量为0.248 mm, 在进气方向上, 即X 轴形变是其主要形变, 为0.230 mm。 在设计IGV 结构和通流设计时需要考虑IGV 叶片形变可能会产生的影响。在流场压力的作用下, 其最大等效应力为24 MPa, 远远低于引起0.2%残余变形的条件屈服强度在20 ℃时为760 MPa。 因此,叶片在强度上满足材料要求。

3.2 IGV 不同工况受力分析

为了能得到外接驱动结构的设计参数（驱动力、 行程等）, 需要计算在流场作用下各工况IGV叶片支反力和支反力矩。 对整个11 种工况的IGV结构叶片形变、 应力、 支反力和支反力矩进行计算分析, 结果见图14～17。

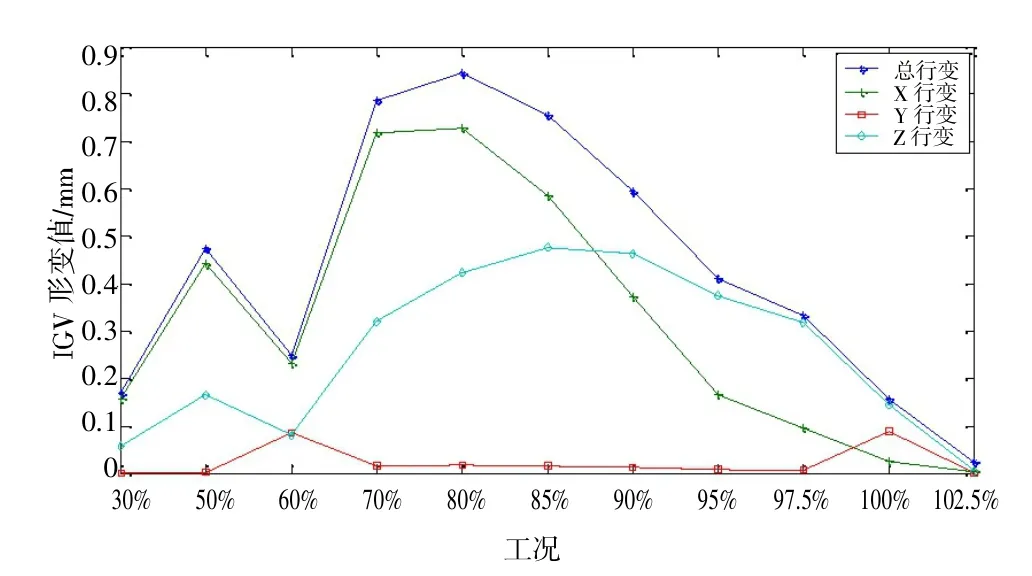
图14 IGV 叶片整体形变值

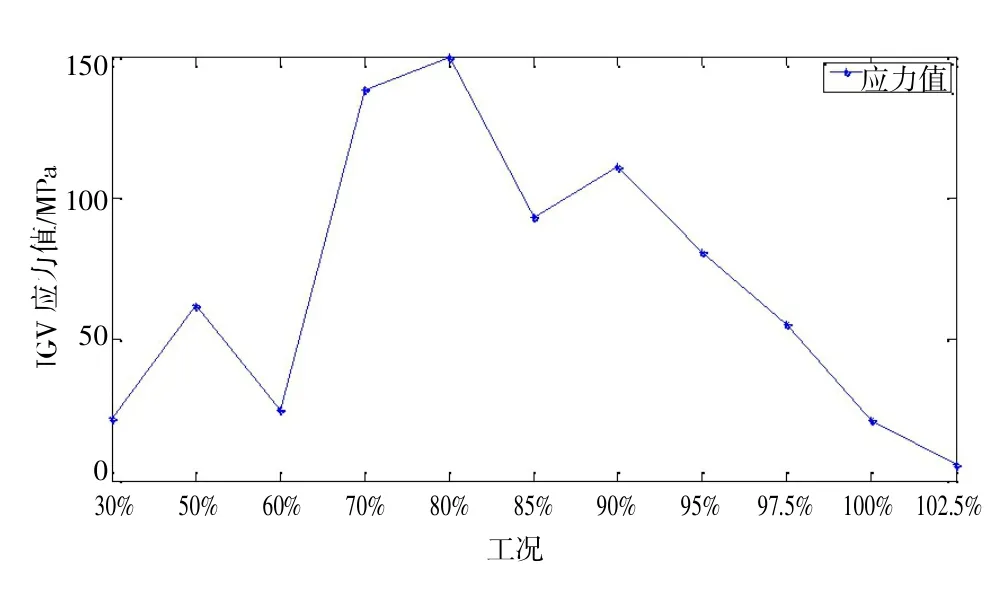
图15 IGV 叶片应力值

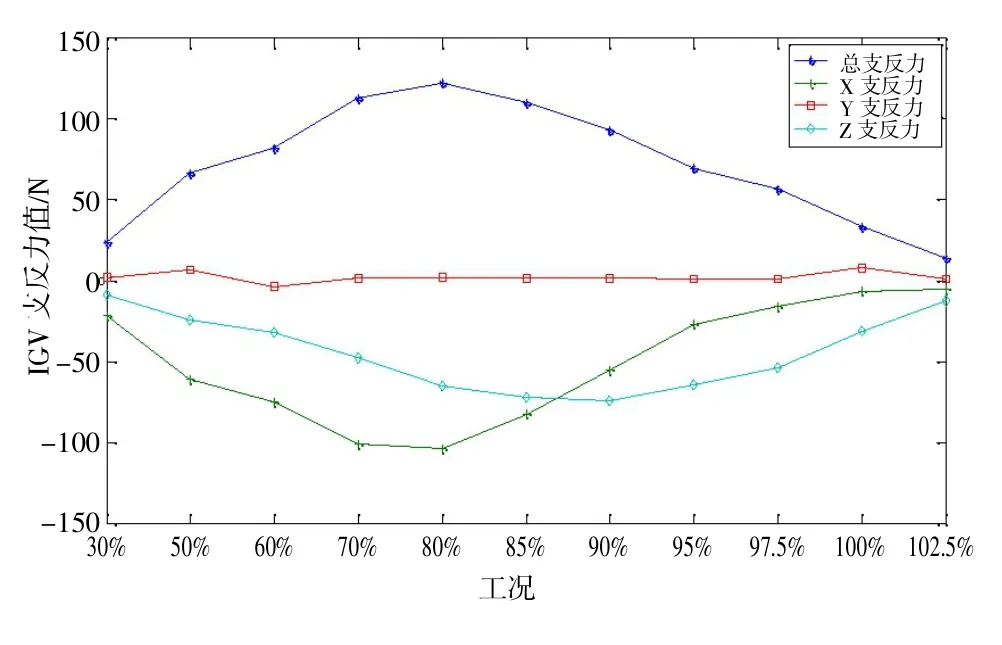
图16 IGV 叶片支反力值

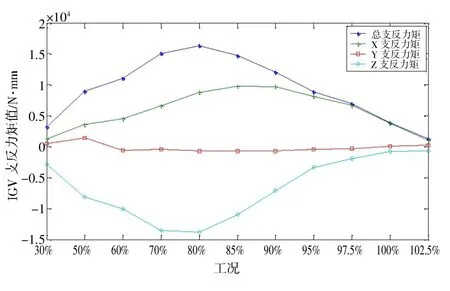
图17 IGV 结构支反力矩值

从图14～17 可以得到以下结论：

（1）IGV 整体形变和X 方向形变最大值都发生在80%转速工况时, 其最大值分别为0.844 mm 和0.730 mm；

（2）IGV 结构应力最大值发生在80%转速工况时, 其值为149.8 MPa, 远小于允许屈服强度760 MPa, 因此IGV 叶片材料满足各工况强度要求；

（3）IGV 结构最大支反合力和最大支反合力矩发生在80%转速工况时, 其值分别为122.13 N 和16 366 N·mm；

（4）考虑驱动扭矩为绕IGV 支撑杆轴线旋转动力, 通过对特定叶片选择和数据处理, 最小驱动扭矩值为1 436 N·mm, 发生在50%转速工况时。

4 IGV 驱动力矩计算

在前面得到了IGV 叶片的支反力矩为1 436 N·mm。 由IGV 叶片所处的环境可知, IGV 叶片转动起来须克服流场作用产生的支反力矩和IGV 叶片与缸体摩擦产生的摩擦力矩,由图18 计算如下：

（a）最大支反力矩（50%转速工况）

单支My=1 436 N·mm,

整圈IGV 叶片的支反力矩为M1=30×My=43 N·m

（b）最大摩擦力矩（80%转速工况）

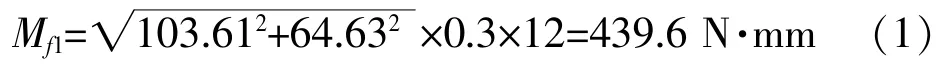
式（1）中0.3 为摩擦系数, 12 为叶片杆半径,103.61 为80%转速工况的Fx, 64.63 为80%转速工况的Fz。

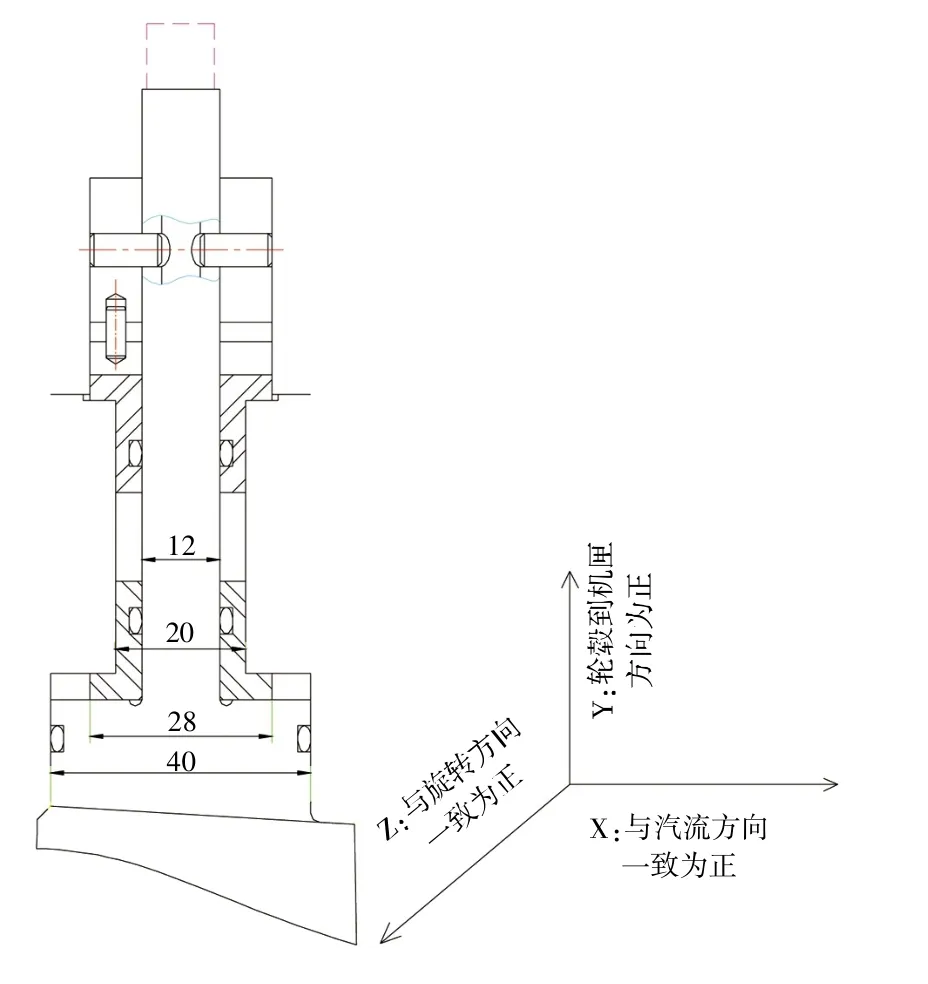
图18 IGV 叶片坐标系

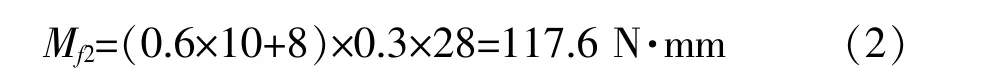
式（2）中0.6 是叶片质量, 8 为80%转速工况下的Fy。

整个IGV 的摩擦力矩为M2=30× （Mf1+Mf2）=16.7 N·m

得到驱动力矩最小为M总=M1+M2=59.7 N·m。

5 总结

本文通过对IGV 导叶做流固耦合计算, 分析认为IGV 可转导叶强度和刚度满足设计要求, 并计算出了IGV 可转导叶整圈总驱动力矩需大于59 N·m, 为驱动机构选型提供了依据。