船体形状因子的数值分析

艾子涛，徐方磊，周广利

(1.中国船级社广州分社 广州审图中心，广州 510235；2.哈尔滨工程大学 船舶工程学院，哈尔滨 150001)

船模阻力试验是长期以来预报实船阻力最常用的方法之一[1-2]。在对试验结果换算过程中会涉及到船体形状因子(1+k)，它对换算预报结果有重要影响[3-4]，一般可通过低速模型试验获得，此时兴波很小甚至趋近于零。现代船舶一般具有球艏或同时具有方艉，船模在低速试验过程中难免产生兴波，同时，受限于实验仪器设备条件，低速状态下的模型阻力不易测准。因此，通过模型试验方法获得精确可靠的船体形状因子(1+k)较为困难。

随着计算机软硬件技术的飞速发展，计算流体力学(CFD)技术在船舶水动力性能预报中发挥着越来越重要的作用[5-10]。其中的叠模方即为将水下部分船体以水线面作为对称面进行对称而形成两个船模叠扣在一起的形式，进而将此形式的船模完全置于水下进行拖曳的方法。该方法免去了兴波阻力的干扰，此时的总阻力即为黏性阻力。然而该方法在试验中实现困难，应用CFD技术计算该方法下的黏性阻力，不但可以避免在物理模型试验中普遍存在的系统误差和偶然误差，还可精确地设定和控制各方向的来流速度，并达到通过叠模数值计算获得黏性阻力、分离出摩擦阻力和黏压阻力、得到船体形状因子(1+k)的目的。

本文选取KCS等3种船型，采用CFD商用软件对其进行叠模低速阻力计算，并将获得的船体形状因子(1+k)分别与通过低速物理船模阻力试验结合普鲁哈斯卡(Prohaska)法、ITTC推荐方法计算得到的船体形状因子进行对比分析，探讨通过CFD叠模计算船体形状因子(1+k)的可靠性。

1 船体形状因子1+k

1.1 1+k原理

为了达到由一定缩尺比的船模试验来预估实船阻力的目的，通常需要选择换算方法。常用的换算方法有二因次换算法(又称弗劳德换算法)和三因次换算法(又称1+k法)。二因次法基于弗劳德假设，其内容为：①船体总阻力可以划分为摩擦阻力和剩余阻力2部分，二者是相互独立的，摩擦阻力只与雷诺数有关，剩余阻力仅与弗劳德数有关，包含黏压阻力和兴波阻力；②船体摩擦阻力可以用相同速度、相同长度、相等湿表面积的相当平板摩擦阻力代替。这样，船体总阻力可以表示为Rt(Re，Fr)=Rf(Re)+Rr(Fr)。

弗劳德假设将不同性质的黏压阻力和兴波阻力合并在一起，称为剩余阻力，并认为适用比较定律，这在理论上是不妥当的[11]。为了在一定程度上克服用相当平板湿面积的摩擦阻力系数或相关线公式的不合理性，同时考虑到船体三维形状与平板的差异所产生的对黏性阻力的影响，休斯提了三因次方法：即船体总阻力可划分为黏性阻力和兴波阻力2种成分，而黏性阻力则可以有相当平板阻力摩擦并考虑到船体三维形状加以修正得到。Ctm=(1+k)Cfm+Crm，式中引入以系数k，称为船体形状系数，并认为k是常量，将同一个k值用于各个速度下的阻力换算，以及用于实船；即在船模(m)和实船(s)总阻系数中分别加上形状阻力系数kCfm和kCfs，另再加上反映粗糙度和某些其他因素引起的阻力成分——换算补贴，连同空气阻力系数等，获得外插的实船总阻力系数。

1.2 通过模型试验获取1+k的方法

传统的基于低速船模试验结果确定船体形状因子(1+k)的方法主要有普鲁哈斯卡(Prohaska) 法和ITTC推荐方法。以上2种方法均假定Fr=0.1～0.2范围内，船体兴波阻力系数Cw与Fr的m次方成正比，其中Cw=yFrm，总阻力系数表达式为

Ct=(1+k)Cf+yFrm

(1)

将式(1)的两边同时除以Cf可得

Ct/Cf=(1+k)+yFrm/Cf

(2)

令Y=Ct/Cf，X=Frm/Cf，b=1+k即有

Y=yX+b

(3)

通过具体的模型试验点数据可以构造一组(Xi，Yi)，i=1,2,…,n，采用最小二乘法进行线性拟合即可求得对应的参数y，b。

构造误差函数:

(4)

使误差函数为最小值的y、b即为所求，令误差函数E(y,b)对y和b的偏导数为0,整理可得

(5)

若选用Prohaska方法对模型试验数据进行处理，则取m=4。根据式(1)～(3)代入试验点数据，通过线性拟合得到直线在纵坐标抽上的截距就是船体形状因子1+k。若选用ITTC推荐方法，则m的取值范围为2～6，可先假定一系列的m值进行计算，其中使误差函数值最小的一组参数即为所求。

1.3 CFD叠模计算获取1+k的方法

由休斯提出的三因次换算方法的主要观点是将黏压阻力与摩擦阻力合并为黏性阻力。这样船体总阻力可以划分为与雷诺数相关的黏性阻力和与弗劳德数相关的兴波阻力2种成分，即

Ct=Cv(Re)+Cw(Fr)

(6)

并且认为黏性阻力系数Cv与摩擦阻力系数Cf之比为一常数，即船体形状系数k。

k=Cpv/Cf或者1+k=Cv/Cf

(7)

由于在CFD叠模计算过程中没有自由液面的影响，计算获得的船体总阻力中没有兴波阻力而只有黏性阻力，这样通过数值模拟计算得到的黏性阻力和基于相当平板理论计算得到的摩擦阻力即可直接求得船体形状因子1+k。

2 CFD计算

选取KCS船、散货船、高速单体船3种比较典型的船型，建立三维曲面模型，进行网格划分和阻力计算。

网格划分对数值计算结果影响很大。根据ITTC的推荐及此前的研究[12]，对船体表面设置hull far、hull near、hull 3个加密区；将y+值选取为100～200；边界层数选取6；模型船体表面第一层网格厚度约为2 mm。最终KCS船、散货船、高速单体船生成网格数分别为340万、380万和300万。

叠模阻力计算采用的是双对称模型，以船模纵舯剖面和静水面作为对称面，求解计算域。流体计算域选用比较常用的尺寸：在船长方向上，从船艏向前延长1个船长，从船艉向后延伸3个船长；在船宽方向上，从主体中纵剖线向两侧各延伸1.5个船长；在高度方向上，从船底向下延伸1个船长。计算域设置分为速度入口边界、压力出口边界，TOP面设为对称面边界，其它边界均设为无滑移固壁边界；船体正浮并且航态固定；流域内为不可压缩流体，其运动满足连续性方程和动量守恒定律；湍流模拟方法应用Reynolds 平均法，湍流模式采用Realizablek-ε模型[13]。

3 计算方案

3.1 KCS船型

该计算模型针对的是一艘KRISO的3 600 TEU集装箱船，标准船模的相关参数、几何模型分别见表1，图1。

表1 KCS船模型参数

图1 KCS船模型

数值计算的模型速度为Vm=0.7、0.8、0.9、1、1.1、1.2、1.3 m/s，对应的量纲一的量化航速为Fr=0.107、0.122、0.138、0.153、0.168、0.183、0.199。叠模计算结果和压力云图(Fr=0.199)分别见表2，图5。Rf，Rv分别为船体的摩擦阻力和总的黏性阻力。

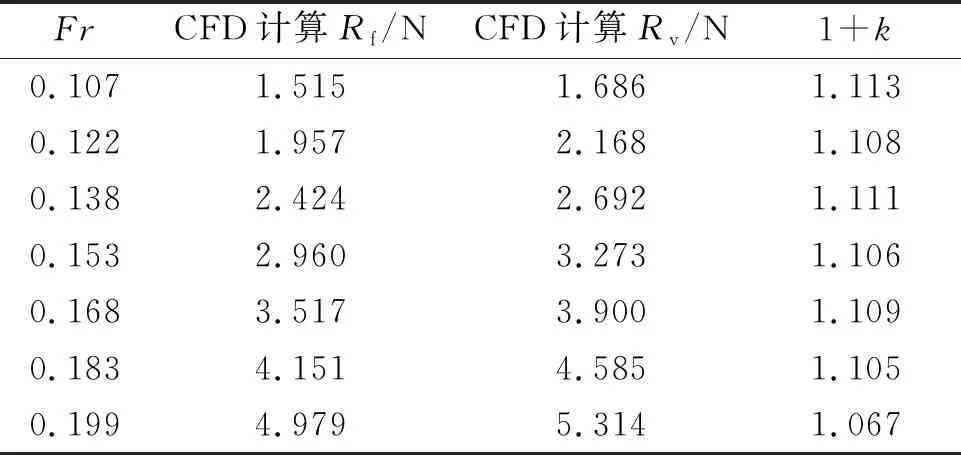
表2 KCS船体形状因子1+k计算结果

将按照式(1)～(4)计算的结果绘于图2、3。

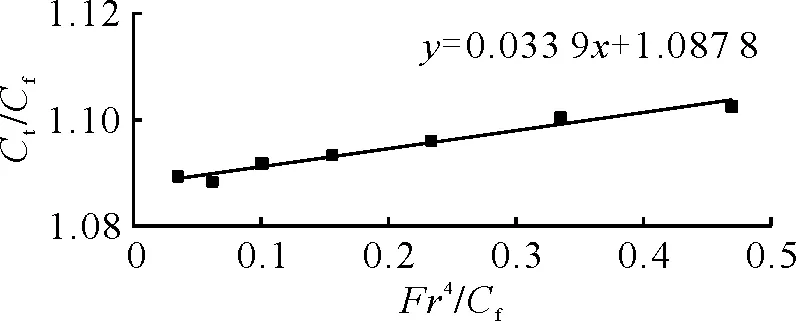
图2 KCS普鲁哈斯卡法(1+k)线性拟合结果

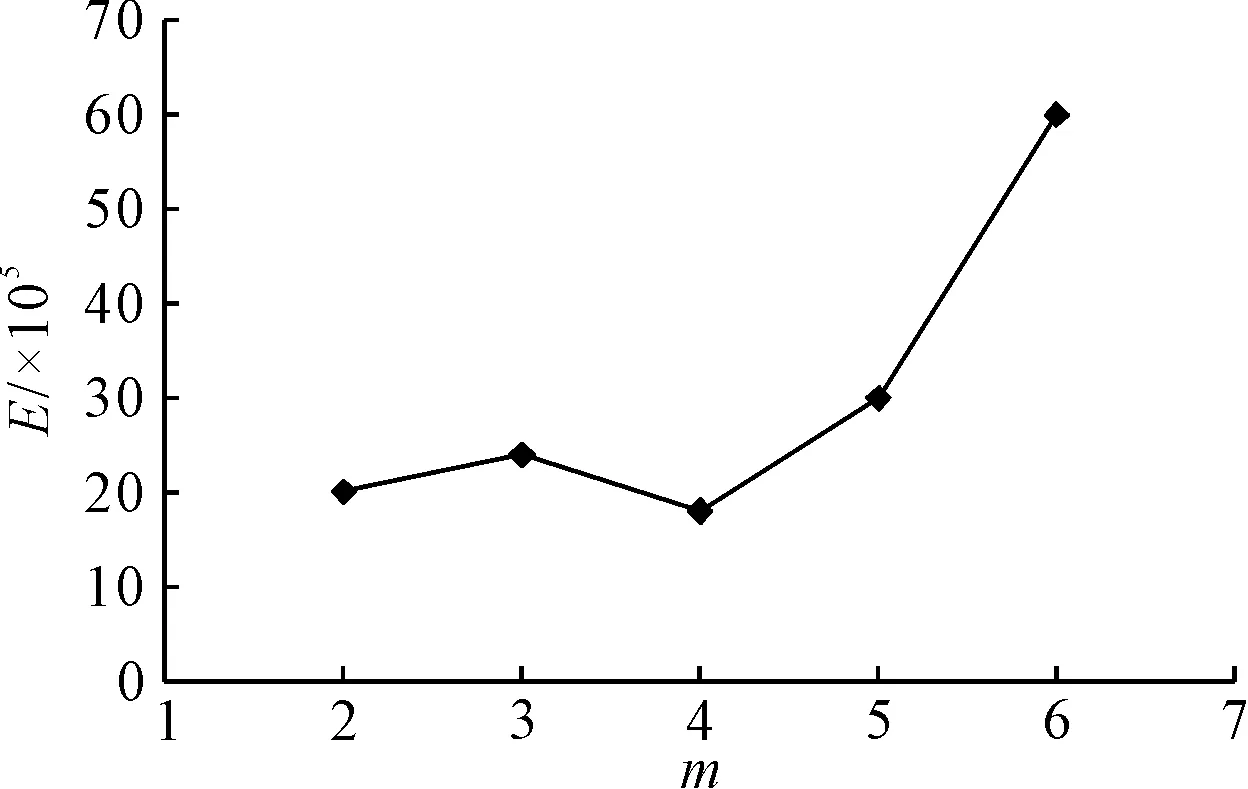
图3 KCS ITTC建议方法线性拟合误差随m的变化

表2为通过数值模拟计算得到的不同弗劳德数下的1+k值。由表2可见，在不同Fr下船体形状因子的1+k的值略有不同，但变化范围不大，上述7个Fr下1+k的平均值为1.103。由图2可知,根据模型试验数据采用Prohaska法计算得到的船体形状因子为1.088。由图3可知，当取m=4时误差函数E值最小，ITTC推荐方法求得的船体形状因子与Prohaska法相同，均为1.088。经比较可得：通过CFD叠模计算得到的船体形状因子(1+k)与Prohaska法及ITTC推荐方法得到的结果相比相差1.2%。

图4为Fr=0.199时，水线以下3 cm平面和船体表面的来流方向压力分布情况。

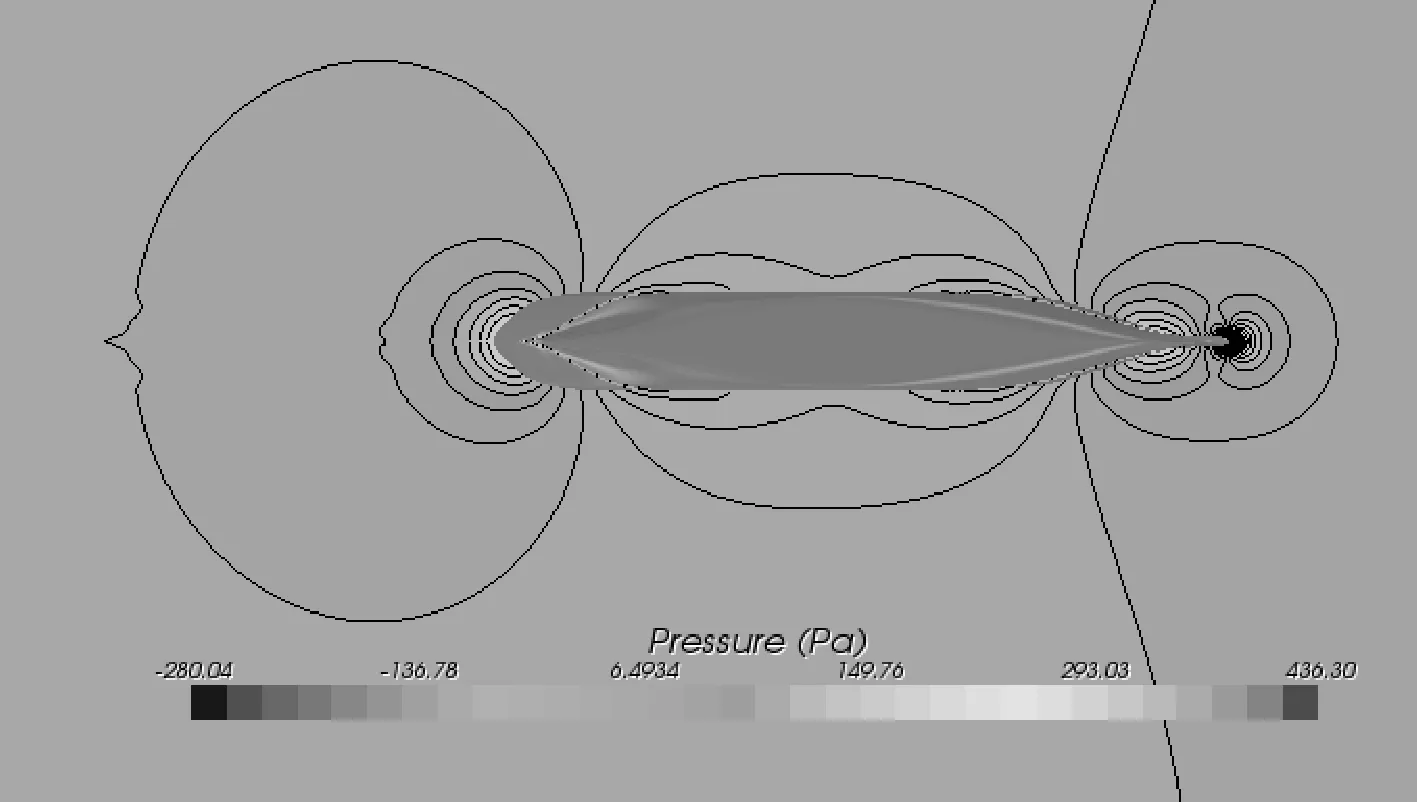
图4 KCS船压力分布云图(Fr=0.199)

由图4及数值计算得到的压力值表明，高压区域位于船艏、艉部，低压区域则位于船体舯部范围内，且分布十分规律。

3.2 散货船

该计算模型针对的是某35 000 DWT散货船，数值模拟计算采取与前述KCS船相同的网格划分及计算方式。船模的相关参数、几何模型分别见表3、图5。

表3 散货船船模型参数

图5 散货船模型

数值计算中的模型速度为Vm=0.75、0.85、1、1.15、1.3、1.45 m/s，对应的无量纲化航速为Fr=0.102、0.116、0.136、0.157、0.177、0.198。叠模计算结果和压力云图(Fr=0.198)分别见表4，图8。Rf，Rv分别为船体的摩擦阻力和总的黏性阻力。

表4 散货船船模1+k计算结果

表4中给出的通过叠合模数值模拟计算得到的6个Fr下船体形状因子1+k的平均值为1.174，利用低速船模阻力试验结果采用Prohaska法和ITTC推荐方法计算得到的船体形状因子(1+k)则分别为1.196、1.197(m=5时求得)，相差分别为1.83%、1.92%。从图8中亦可看出, 沿船长分布的高压区域位于艏、艉部，低压区域则位于船体舯部范围内，且分布较为规律,无压力突变的区域。

图6 散货船普鲁哈斯卡法(1+k)线性拟合结果

图7 散货船ITTC推荐方法线性拟合误差随m的变化

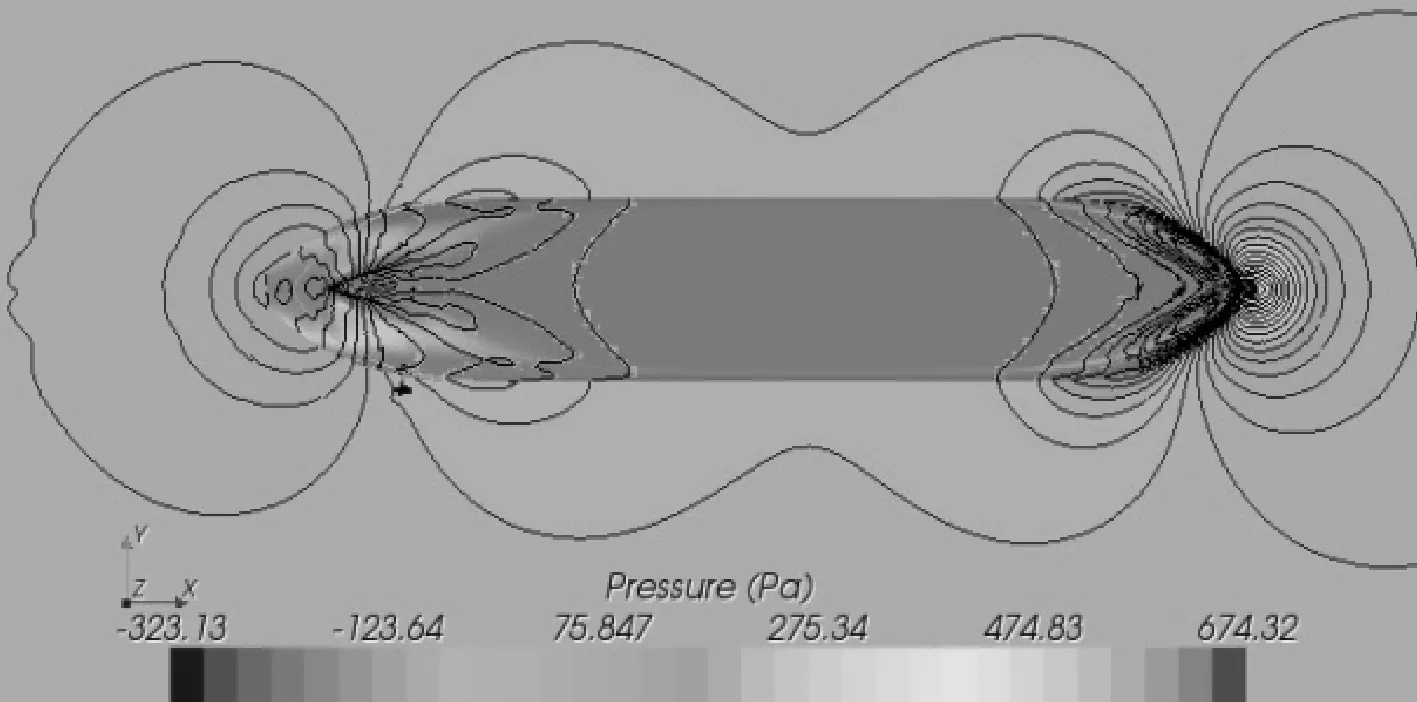
图8 散货船压力分布云图(Fr=0.198)

3.3 某高速单体船

计算模型取自某高速单体船，亦采取与KCS船相同的网格划分及计算方式。船模的相关参数、几何模型分别见表5，图9。

表5 某高速单体船模型参数

图9 高速船模型

数值计算中的模型速度为Vm=0.6、0.7、0.8、0.9、1 m/s，对应的量纲一的量化航速为Fr=0.111、0.129、0.147、0.166、0.184。叠模计算结果和压力云图(Fr=0.184)分别见表6，图12。Rf，Rv分别为船体的摩擦阻力和总的黏性阻力。

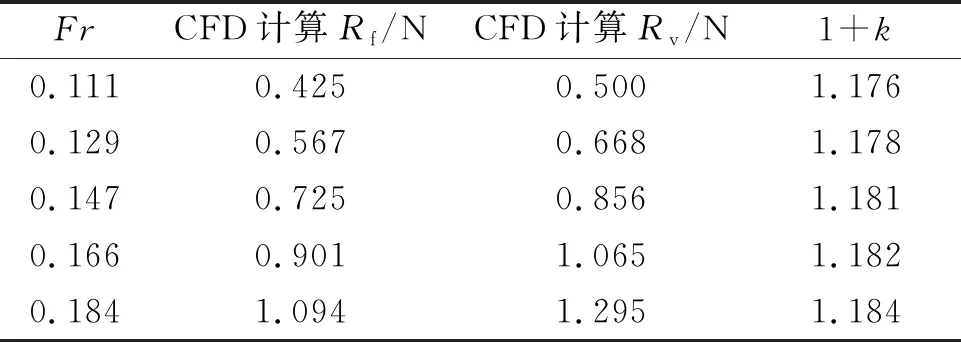
表6 高速船1+k计算结果

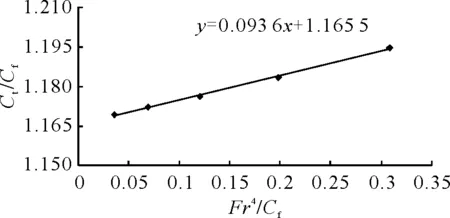
图10 高速船普鲁哈斯卡法(1+k)线性拟合结果

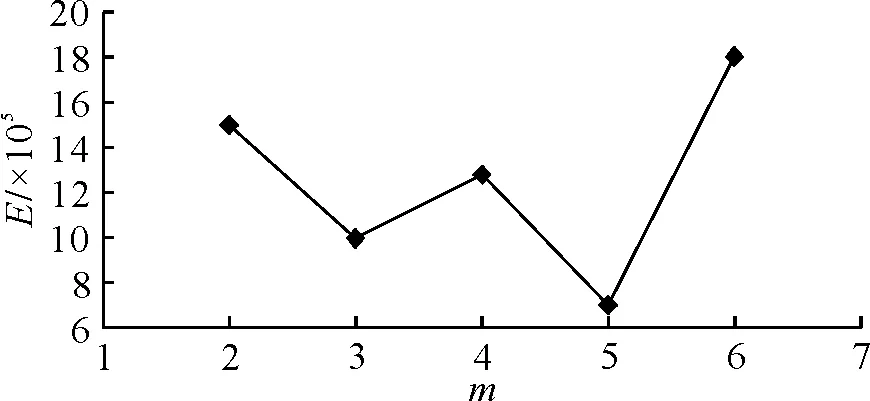
图11 高速船ITTC推荐方法线性拟合误差随m的变化

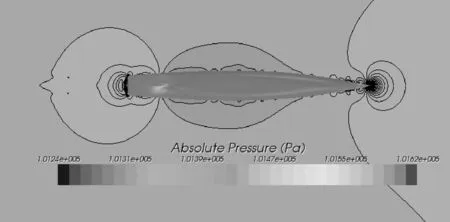
图12 高速船压力分布云图(Fr=0.184)

表6中5个Fr下1+k的平均值为1.18，采用Prohaska法和ITTC推荐方法计算可得(1+k)分别为1.166、1.168(m=5时求得)，相差分别为1.4%、1.02%。由图12可见,高压和低压区域与上述KCS和散货船类似,但沿船长压力改变区域较小且在船艏艉及舯部有若干小的突变区域,这主要是由于船体比较瘦长,长宽比较大。

4 结论

1)采用CFD叠模计算方法得到的船舶低速航行时摩擦阻力结果与理论计算值较为吻合，表明利用CFD叠模法计算摩擦阻力以及船体形状因子(1+k)具有一定的可行性，可为高速下的船体形状因子(1+k)的计算提供计算基础。

2)从压力云图可以看出，沿船长方向高压区域位于船艏、艉部，低压区域则位于船体舯部范围内，各区域压力分布的较为均匀，无较大压力突变的地方，从最终结果来看，叠模计算船体形状因子(1+k)与理论计算及物理模型试验也十分贴近。

3)针对KCS船型、散货船、高速单体船而言，基于CFD叠模计算的船体形状因子与模型试验测得形状因子十分接近，具有较高的工程应用价值。但本文进行计算和验证的船型有限，对于其他船型(比如多体船等)有待后续研究。