一种船舶组合导航系统混合误差模型及应用

庞玺斌，梁成程，张闯

(大连海事大学 航海学院，辽宁 大连 116026)

支持向量机(support vector machine，SVM)作为一种线性和非线性建模的回归算法已经得到了广泛应用，但是这种方法忽略了可能导致系统整体误差增长的误差派生滤波器。SVM能够基于较少的训练数据定义模型，具有实时性。对过度拟合问题的鲁棒性表现出优越性，并且不需要噪声模型的先验知识。基于此，考虑建立一种混合模型，利用SVM对线性误差的KF输出进行建模，并且应用FOS作为自回归(autoregressive，AR)建模算法对非线性误差进行建模。利用SVM对多个候选集进行检验，得到在GPS失效条件下可以替代KF的最优训练模型。此外，基于AR思想，将计算出的非线性方位误差传递给FOS[1-3]。当GPS失效[4-5]时，算法开始预测阶段运行这两个模型。SVM开始估计线性方位误差取代KF[6-8]，而FOS自回归估计方位角的非线性误差。

1 GPS/RISS组合导航

船舶的纵倾角(β)和横摇角(γ)表示为

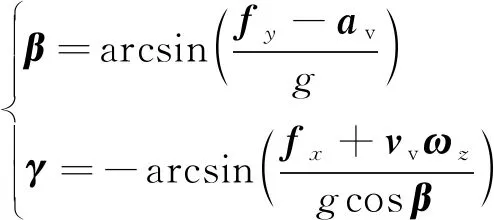
(1)

式中：av为船舶的实际加速度；fx和fy分别为横向加速度量测量和前向加速度量测量；ωz为垂直陀螺仪量测量；g为重力加速度。

为了给出方位角(Az)，需要对垂直倾角和地球角速率(ωe)的影响进行补偿，以计算船舶相对于北向的方位角。

(2)

式中：ve为东向速度分量；φ和h分别为纬度和高度，RN为地球椭球曲率半径。速度分别沿东向、北向(vn)和垂向(vu)的分量为

(3)

其中：vv为船舶速度。根据式(4)计算位置的纬度、经度和高度。

(4)

式中：RM为地球椭球曲率的子午线半径。

3D-RISS使用2个加速度计代替陀螺仪来获得纵倾角和横摇角。加速度计产生的误差比陀螺仪小，累积位置误差随时间变化与惯性误差参数之间的关系如下。

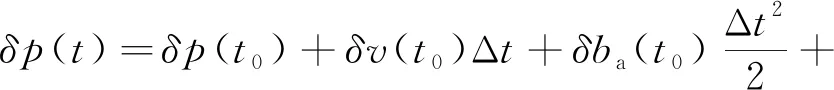
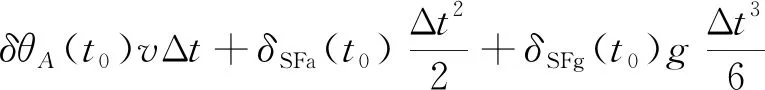
(5)

式中：δp(t)为时间t位置误差漂移；δp(t0)，δv(t0)为初始速度误差；ba(t0)和δSFa(t0)分别为初始加速度计偏移偏差和换算系数误差，δbg(t0)和δSFg(t0)分别为初始陀螺仪偏移和换算系数误差；δθr,p(t0)和δθA(t0)分别为纵倾/横摇和方位角误差引起的初始非正交误差；v为平均速度。

KF同GPS组合提供减少惯性误差所需的差值，但在GPS失效时，误差仍然存在。非线性误差的估计可以用来限制GPS失效期间误差的快速积累。

由于使用速度传感器读数代替加速度计，计算的速度对RISS有一定的改进。基于加速度计的速度计算引入了与t成比例的速度误差和与t2成比例的位置误差。另一方面，基于速度传感器的速度计算只需一次积分，最终提高位置误差。同样的关系也适用于GPS失效期间。因此，方位角误差是三维RISS中陀螺垂直对准误差的主要来源。误差非线性估计是限制GPS失效期间误差快速积累的方法之一。同时，失效期间KF辅助提供的解提高了KF的估计性能。

KF实现需要对系统误差模型进行辨识。由位置误差(δφ，δλ，δh)、速度误差(δve，δvn，δvu)、方位误差(δAz)和传感器误差(δav，δωz)组成的RISS误差状态矢量。利用RISS方程的Taylor级数近似，将这些误差表示为微分方程。误差模型可以表示为

(6)

(7)

(8)

式中：Δ(·)为相应的高阶误差。

由于所提出的系统具有GPS，因此,其测量可以用于初始化过程。如果船舶在初始化过程中是静止的，则速度矢量初始化为零。另外，在动态条件下，GPS测速量测量用于初始化速度矢量。

姿态对准分为2步。平台通过纵倾角和横摇角的初始化来调平，陀螺罗经用于初始化航向或方位角。当船舶静止时，加速度计通过纵倾和横摇来测量由于水平面倾斜而产生的重力分量。整个IMU的加速计量测量表示为

(9)

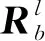
由于RISS中仅使用2个加速计，因此,定义纵倾和横摇为

(10)

纵倾和横摇需分开计算，定义方位角为

(11)

2 建模算法

2.1 支持向量机(SVM)

假设训练数据集D={(a1,b1),(a2,b2),…,(al,bl)}⊂Rn×R。其中，ai和bi分别表示输入矢量和输出矢量；下标l为训练集大小。支持向量机回归的目的是识别一个实数函数f(a)，用于估计任何输入向量(a)的输出(b)。求解算法基于非线性映射Φ的高维空间F中执行回归，以保证输入向量(a)映射到该空间。

f(a)=WTΦ(a)+c

(12)

式中:Rn→F，W∈F。

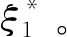
(13)

式中：i=1，2，…，l。

用非负Lagrange乘子vi，ηi构造Lagrange函数(L)作为对偶公式，则式(13)可以写为

(14)

基于Karush-Kuhn-Tucker(KKT)条件识别式(14)中的参数v和c，利用核函数K(ai,aj)，得到最终的近似解为

(15)

以处理后的数据为模型输入，采用SVM对KF估计的线性方位误差进行建模。选择高斯径向基函数(RBF)作为核函数，主要是因为其精度满足要求，而且易于实现。因此，f(a)表示线性方位误差，ai表示时刻i的模型输入数据集。

2.2 快速正交搜索(FOS)

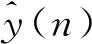
(16)

FOS通过迭代搜索N个可用的候选基函数，选择M个最显著的函数，降低均方误差(MSE)。FOS算法利用(gram schmid，GS)正交化原理识别从pm(n)函数中生成的正交候选qm(n)，并利用系数gm(n)降低量化误差。GS算法产生一个新的正交集，模型为

(17)

FOS通过GS系数的隐式确定降低了正交函数定义所需的时间，GS系数是使用平均时间而不是逐点计算得到的。通过正交展开权重和GS系数识别出原始权值km。当模型误差小于可接受值时，正交函数辨识的FOS迭代过程停止。由于FOS正交候选非直接计算，因此,模型的建立速度非常快。

本文非线性方位误差建模是FOS算法的任务。如图1所示，非线性方位角误差的自相关函数在整个测试轨迹中显示出高相关性。因此，对于非线性方位角误差的建模，采用AR概念使候选解表示先前计算的非线性方位角误差。这种方法降低了使用KF输出作为候选的不确定性。训练瞬间i的非线性方位角误差用y(n)表示，而pm表示由先前的非线性方位角误差(m=1，2，…，i-1)构造的模型候选解。

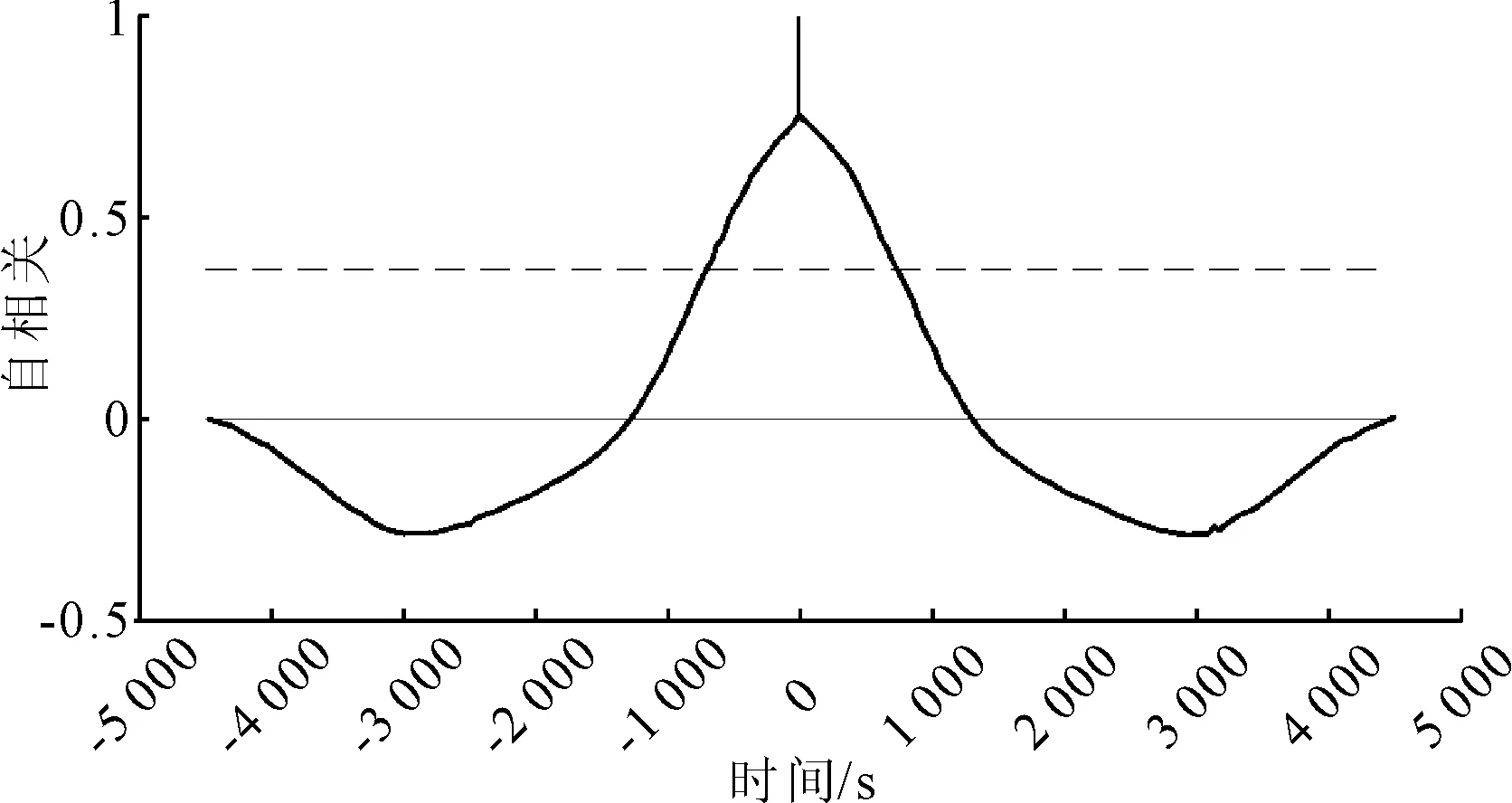
图1 非线性方位角误差自相关函数

3 混合误差模型

基于FOS的强化KF-FOS算法是对非线性方位误差进行建模，此方法使用KF估计的线性误差作为模型的候选。在模型训练过程中，将KF的输出传递给FOS来建立非线性模型。在GPS失效期间，用于估计非线性误差所需的模型线性误差在预测期间通过KF传递，但缺少GPS更新。此方法产生的模型具有影响定位精度的相关不确定性。

为了减小GPS/RISS组合系统的位置误差，提出SVM-FOS混合建模算法，分别对KF输出和方位残余非线性误差进行建模。当GPS失效期间，隔离独立KF输出对最终导航结果的影响。通过利用SVM对GPS辅助时的KF输出进行建模，并在GPS失效时替换KF而实现的。同时，在GPS失效时，基于AR概念利用FOS对非线性方位误差进行建模。考虑到KF输出为线性误差，本方法使得模型能够在GPS失效时不使用KF预测来估计线性和非线性误差。见图2。

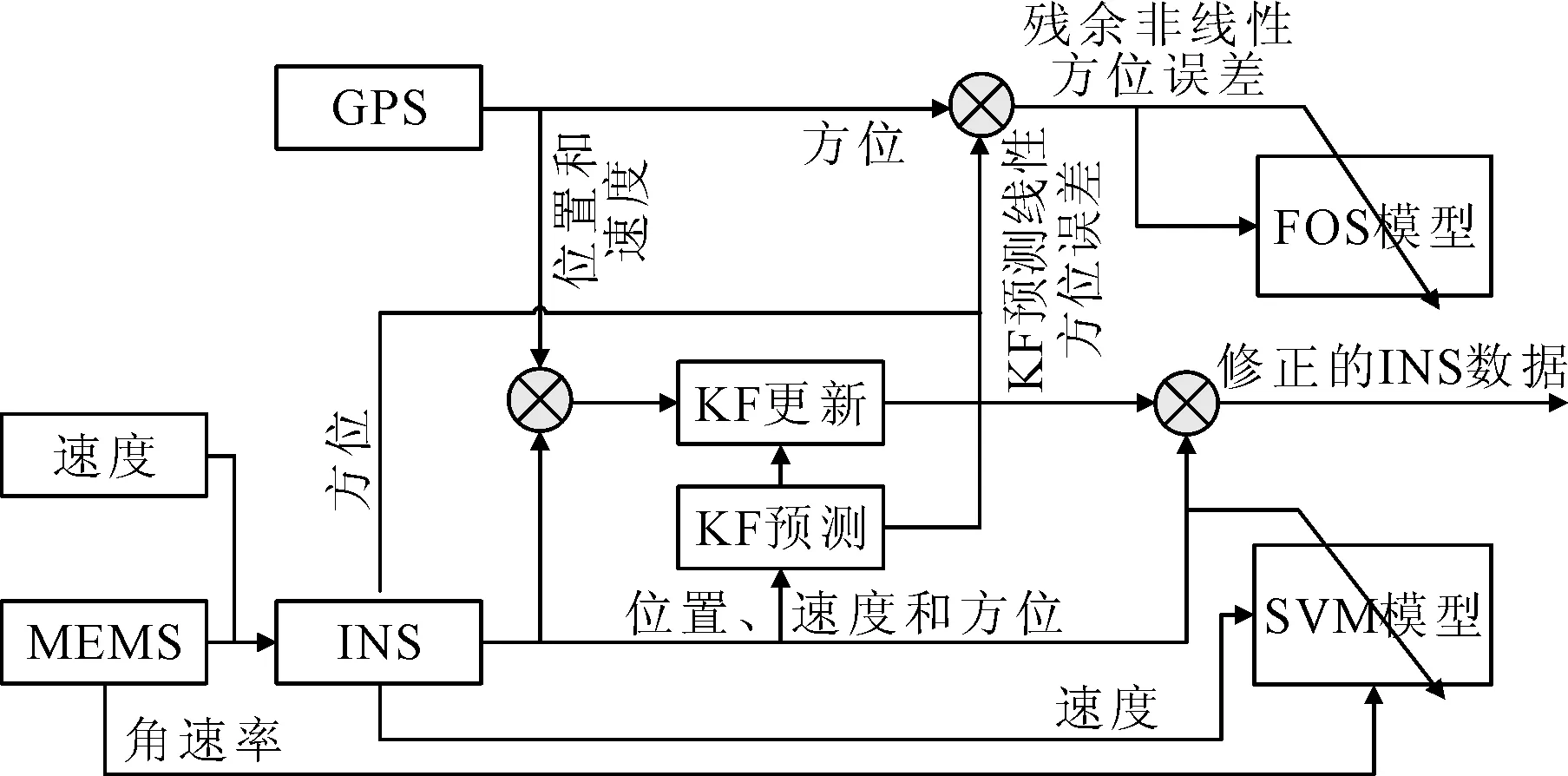
图2 SVM-FOS混合方法原理

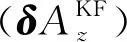
(18)

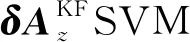
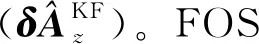
(19)

估计方位将速度传感器量测量传递到另一个解算算法中(图3中的INS解算II)以计算校正的导航数据。由于本算法不依赖于GPS失效的KF输出，因此，KF在没有任何GPS更新的情况下仍预测。在GPS更新过程中，对于传感器误差而言，KF线性化模型取决线性随机模型，并不影响系统精度。在重新捕获GPS辅助信号后，KF预测能够加速收敛。

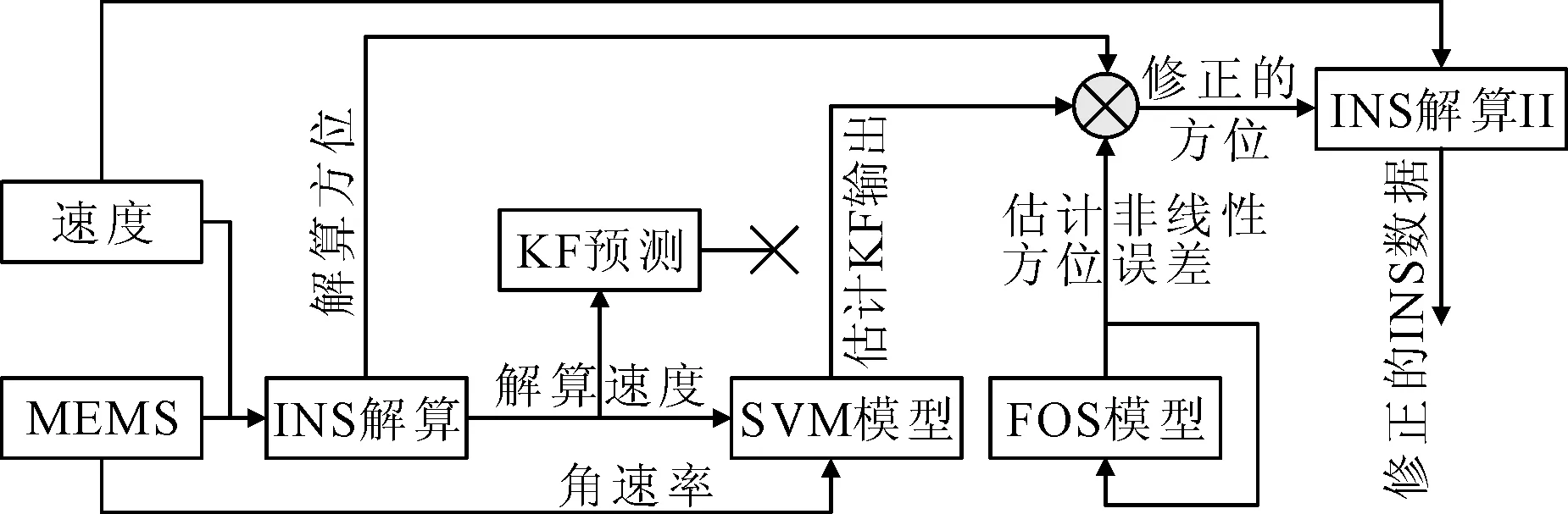
图3 GPS失效时SVM-FOS混合方法

4 仿真结果与实验分析

4.1 仿真结果

结合海试来评估所提出的导航解的性能。实验在大连港附近进行，天气晴朗，风力3级，微浪。从计程仪获取以1 Hz采样率采集的船速数据，从Crossbow MEMS级IMU 100陀螺仪(性能参数见表1)的垂直角速率得到方位量测量。

为了评估系统性能，采用NovAtel提供的G2 Pro-Pack SPAN装置提供参考导航解。通过与参考解比较，验证系统的整体性能。测试轨迹见图4a)。在后处理过程中，模拟8个300 s长的GPS数据丢失，以实现对系统定位精度的评估。模拟其中2、4、6和8号GPS失效时的轨迹,见图4b)。

表1 IMU的性能参数

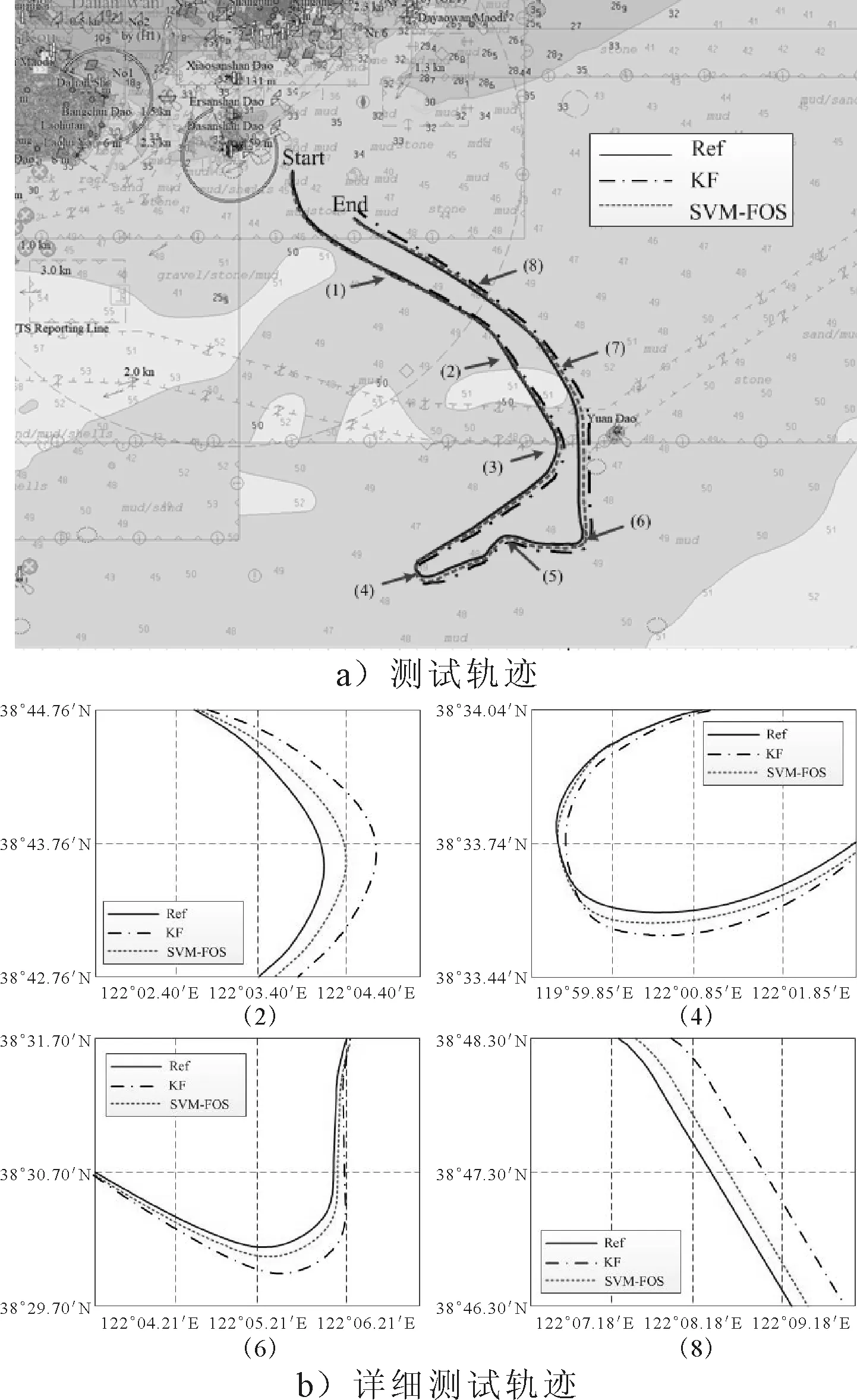
图4 测试轨迹

将提出的SVM-FOS混合方法的估计导航解与文献[16]提出的FOS方法进行比较，还包括每种方法相对于参考解的位置RMSE的比较,结果表明，增强KF-FOS方法提高了方位精度，获得了比仅使用KF更好的性能。

4.2 组合导航系统实船分析

为了在SVM训练过程中得到一个更精确的KF模型，在系统实现中对不同的候选解进行对比。由于SVM是建立在统计学习理论的基础上，因此，加入更多的候选对象目的是开发出更稳定的模型，特别是当这些候选对象描述了更多关于拟合参数的信息。整个训练期间，模拟失效以得出所需的结果。如图5所示，将不同的模型输出与KF输出作为模型数据进行比较，较好的训练结果来自第三模型SVM3。显然，SVM3模型跟踪了模型数据的变化，得到的模型与实际数据的误差最小。因此，SVM3所提供的最佳结果可用于描述线性方位误差的信息量更优的候选集。选择SVM3中的所有候选(ve，vn，wz)是因为其与线性方位角误差有直接和间接的关系。在对SVM3选项进行信任后，选择该选项以供提出的解使用。

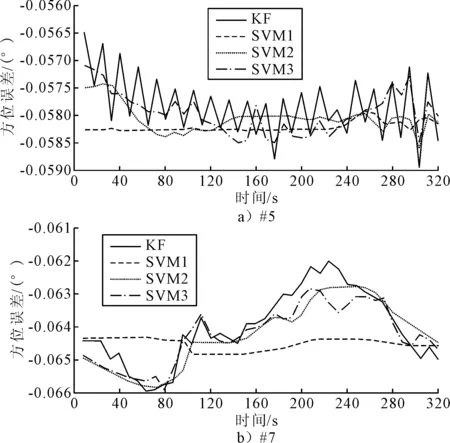
图5 SVM模型训练输出与实际KF输出的比较

将非线性方位误差的2种FOS模型与实际数据进行比较。利用基于AR思想的SVM-FOS方法构造非线性误差模型同以KF估计线性误差作为模型候选的KF-FOS增广方法进行比较。如图6所示，SVM-FOS比KF-FOS具有更好的训练性能，KF-FOS未能选择候选对象识别模型，而SVM-FOS方法成功地定义了模型。比较结果表明，在失效时，所提出的方法能够识别模型候选者，不仅有助于抑制方位误差，而且可以提高定位精度。

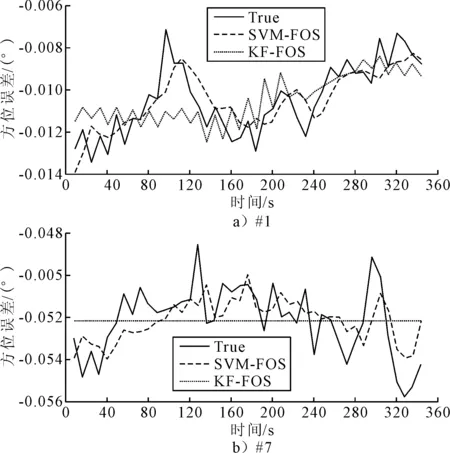
图6 FOS不同方法的培训输出

如图7所示，本文提出方法的总体性能与其他基于位置RMSE的方法进行比较。结果表明，SVM-FOS算法在定位精度上取得了较好的效果，提高了导航解性能。提出的算法RMSE可以与增广KF-FOS方法相媲美，对结果进行深入分析表明，该方法较好地抑制了一些峰值误差。

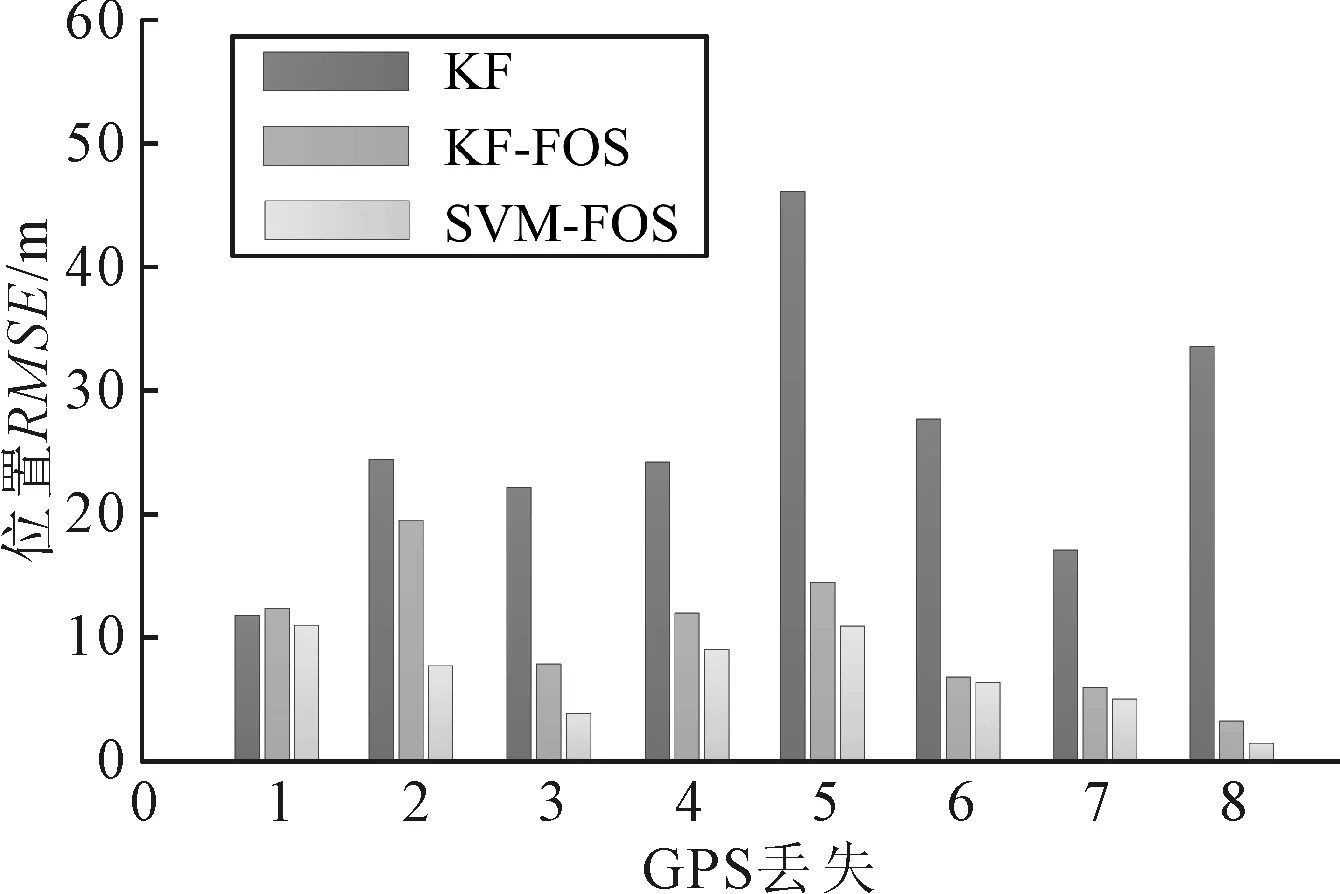
图7 FOS不同方法的培训输出

系统的总体性能表明了方位误差的重要性及其对位置误差的影响，并且在MEMS应用中，表明了非线性残余误差对位置误差的影响。利用MEMS惯性传感器处理常用的KF组合方法导致系统产生漂移。提出的混合SVM-FOS误差模型成功地替代了GPS失效时的KF模型，实现了基于SVM模型的线性误差估计。同时，基于AR思想的FOS给出了非线性方位误差的稳定模型。

混合模型在GPS失效期间获得的平均位置RMSE为6.2 m。将算法与强化KF-FOS进行比较，其平均位置RMSE降低了2.7 m。

GPS失效期间的船舶航行速度见图8。在第1次失效期间，混合建模方法在RMSE上比KF方法降低了约77%。而第6次失效期间，船舶转向，速度发生了变化，使用混合模型方法比KF算法的位置RMSE降低了约94%。此外，增强KF-FOS方法在第2、5、7和8GPS失效时不能有效选择模型的候选解。在GPS失效期间，本文算法能够识别非线性模型候选解，并且位置RMSE比增强KF-FOS方法降低约11%。

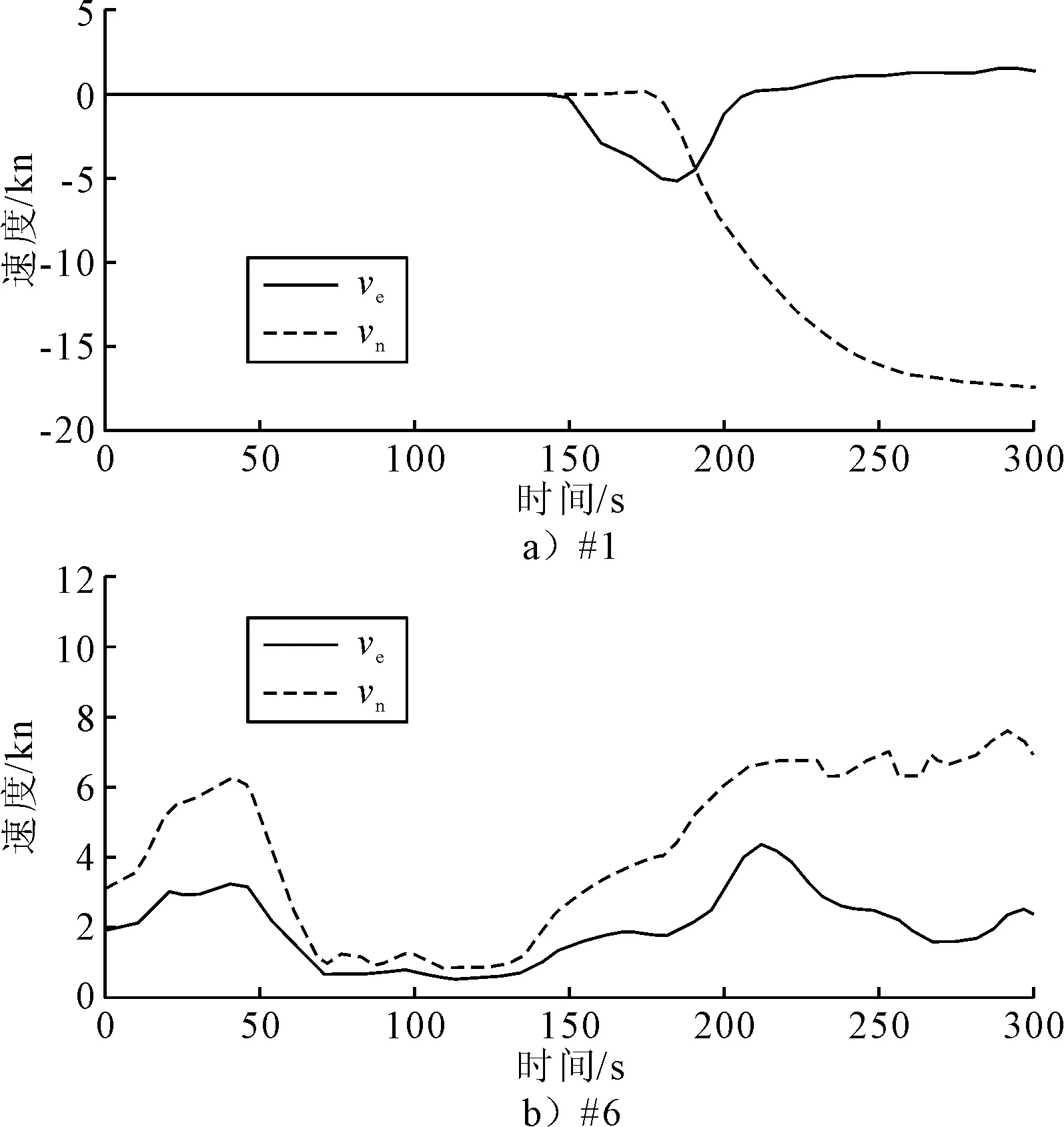
图8 北向和东向速度

5 结论

混合误差模型利用SVM和FOS两种方法来估计并消除GPS故障时MEMS陀螺仪的误差，而无需使用KF输出。成功地将GPS失效期间的位置RMSE最小化。此外，将AR方法和FOS方法结合，在候选的解选择和模型准确性方面都取得了较好的效果。

测试结果与理论预期相符，并证明了该算法在GPS失效期间的良好性能，其位置RMSE降低率约75%。此外，该算法通过获得更好的精度，显示出优于增强KF-FOS融合技术，并且位置RMSE降低了约30%。