基于支持向量机的船舶感应电机轴承故障在线诊断方法
薛征宇,郑新潮,邱翔,邱赤东
(大连海事大学 船舶电气工程学院,辽宁 大连 116026)
感应电机是船舶电力系统、动力系统的重要支撑设备,当电机出现故障时,会危及船舶营运的安全。其中,轴承故障占中小型感应电机故障的69%以上[1]。由于船舶振动源多、干扰源多的特殊工作环境,成本相对较低的振动诊断方法不太适合应用于船舶感应电机轴承的故障诊断。已有的研究中快速傅里叶变换[2]是一个非常简单快捷的频域分析方法,但是由于电机轴承故障信号通常被电力系统的基波及其谐波的强噪声背景所覆盖,因此,直接通过传统的傅里叶频谱分析方法很难在线判定电机轴承故障[3-4]。小波变换可以提供信号的时间和频率数据,具有对信号进行局部分析的能力,变大变小的窗口,可以提供更好的分辨率。但是小波和小波包[5]方法计算量大,而且小波分解子带的频率分析范围覆盖一定的频段,在处理轴承故障的弱特征信号时可能会出现较大的偏差[6]。经验模态分解(EMD)在分解过程中可能产生模态混叠现象且其去噪过程过于粗暴[7]。信号功率谱密度估计的WELCH分析法通过分段数据的重叠和加窗可以降低谱的方差,通过选择加窗的不同改变分辨率,使谱估计在满足分辨率高和方差小的一致性条件下取得良好的效果,可解决在低信噪比条件下提取轴承故障特征信号的问题,且计算量相对较小,提取轴承故障特征信息平稳。因此,为了实现电机轴承故障的低成本在线诊断的目的,考虑利用WELCH法的平稳性和计算量相对小的特点,通过试验,合理选取适合感应电机滚珠轴承故障特征提取的WELCH法中的窗函数,可有效避免由于算法导致的故障特征提取的干扰。
通常离线的检测是人工识别故障特征频率,要实现在线检测则需要采取机器学习的方式。目前,常见的机器学习算法是神经网络和支持向量机[8-10]。现有的轴承监测系统大多存在结构复杂、多设备冗余、成本昂贵、需解体安装等问题,而且某些电机拆卸和安装比较困难。这里提出一种基于周期图WELCH分析法与支持向量机相结合的方法来实现电机轴承故障的在线诊断。由于WELCH分析得到的单一频域特征易受到外部条件的干扰,且不同特征对故障的敏感度不同,在滚动轴承的电流检测中,依据单一特征量识别轴承状态,其效果往往不够理想,为保证识别方法对故障敏感且有较好的鲁棒性,从WELCH分析中提取峰度、偏度、波峰因数、间隙和形状因子为支持向量机的特征向量,通过实验优化核函数参数,实现轴承外沟道故障的识别。
1 理论分析
1.1 轴承外沟道损伤特征频率
电机的轴承在长期运行之后,会出现表面疲劳,进而形成单点损伤,该损伤将会产生周期性的脉冲振动,振动信号的幅度和周期取决于电动机的转速、轴承损伤的位置,以及轴承的尺寸等。
电机轴承的单点损伤分为外沟道损伤、内沟道损伤、钢球损伤、保持架损伤4种类型,根据不同的损伤部位,所体现出来的故障特征频率也不同。本文重点针对外沟道损伤故障。外沟道故障振动频率为
(1)
式中:n为钢球的数量;fr为转子机械频率;BD为钢球的直径;PD为轴承节圆直径;β为钢球和沟道之间的接触角。
由于轴承上的外沟道损伤缺陷,使得电动机阻力矩产生变化,从而在电流频谱中出现特征频率。轴承振动频率反映到定子电流特征频率为
fcf=|fs±mfc|
(2)
式中:fs为供电电源频率;m=1、2、3。
1.2 基于WELCH分析的轴承故障特征提取
采用WELCH方法提取轴承故障特征。该方法将信号分成K个段,针对每个分段数据进行加窗处理,求取周期图,最后求得K个周期图的平均值。选用不同的窗函数时,分辨效果不同。通过试验,选取适合感应电机滚珠轴承故障特征提取的WELCH法中的窗函数Blackman窗,旁瓣衰减速度大,频谱泄漏小,在分段数及数据点数相同的情况下可有效提取轴承故障信号。WELCH的计算公式如下。
设xi(n)为电机电流信号,
xi(n)=x(iD+n)ω(n)
0≤n≤L-1,0≤i≤K-1
(3)
式中:ω(n)为长度为L的窗函数;D为偏移量;n为时间;i为第i段。
(4)
(5)
其中:N为样本长度。
第i段的周期图为
(6)
WELCH谱分析为
(7)
从WELCH分析中提取以电流特征频率为中心频率的特定间隔频带,以构建特征矩阵。轴承的电流特征频率按式(2)计算。考虑到能量泄漏,每个特征频率以2 Hz频带表示,[fCF-1,fCF+1]。
能够用于表征故障特征的参数有限,在选取时遵循高敏感性、高可靠性、可实现的原则。选取峰度xkr,k、偏度xsk,k、波峰因数xcr,k、间隙xcl,k,形状因子xsh,k5个参数,定义如下。
(8)
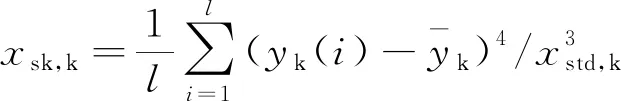
(9)
xcr,k=max(yk(i))/yrms,k
(10)
xcl,k=max(yk(i))/ysmr,k
(11)

(12)

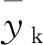
向量机输入特征矩阵X如下。
(13)
1.3 支持向量机
SVM是基于统计学习理论的二类分类方法。给定训练样本集,D={(xi,yi),i=1,2,…,l}xi∈Rd,每个样本属于y={+1,-1}中的一类,训练样本集由超平面线性可分,则分类器的超平面方程为
ωxi+b=0
(14)
式中:xi为训练向量;ω为法向量;b为超平面的偏移。此时将两类样本正确划分并使分类间隔最大化的优化问题可转化为在yi(ωxi+b)-1≥0的条件下,求解
(15)
因线性不可分,需要加入松弛变量ξi≥0,此时则约束条件为yi(ωxi+b)≥(1-ξi),为能得到区分样本并使分类间隔最大的最优分离超平面,需考虑以下优化问题。
s.t.yi(ωxi+b)≥1-ξi
(16)
式中:C为惩罚因子。
轴承故障诊断数据集是线性不可分的,引入拉格朗日乘子αi≥0和卡罗需-库恩-塔克(KKT)条件,通过在最优超平面中引用适当的核函数K(xi,xj),将低维空间非线性问题转化为某个高维空间的线性可分问题,则最大化问题变为
(17)
这里选用高斯径向基核函数。
(18)
式中:σ为核函数参数。
则分类决策函数如下。
(19)
超平面方程如下。
本文定义:故障轴承的类叫正类,正常轴承的类叫负类;TP,将正类预测为正类;FN,将正类预测为负类;FP,将负类预测为负类;TN,将负类预测为正类;模型的评价指标是准确率A、精确率P、召回率R。
(21)
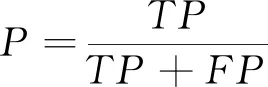
(22)
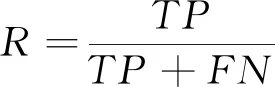
(23)
2 实验验证
2.1 实验电机及轴承参数
额定电压为380 V,额定电流为5.03 A,额定功率为2.2 kW,额定转速为1 430 r/min,其驱动端轴承型号为6206。
利用电火花机对轴承进行人为模拟损伤,在外沟道制造长度为4.32 mm、宽度与深度为1 mm的外沟道损伤故障。故障轴承损伤程度见图1。

图1 外沟道损伤轴承示意
6206型轴承钢球的个数N=9,节圆直径PD=46 mm,钢球直径BD=9.6 mm。
根据公式(1)和式(2),计算电机轴承的振动故障特征频率值为84.9 Hz,对应的电流特征频率分别为34.9、119.7、134.9、204.6、219.7和304.6 Hz。
2.2 诊断系统硬件结构与故障诊断流程
试验系统是以TMS320F28335 DSP 为核心处理器,系统原理见图2。
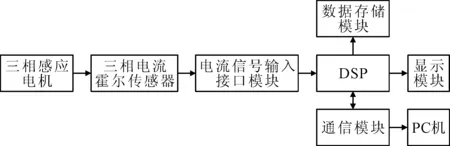
图2 在线诊断系统原理
实验中搭建的感应电机轴承故障试验平台主要由感应电动机同轴连接发电机,发电机连接三相电阻负载构成;传感器采用IT 60-S型非接触式霍尔传感器,测量范围60 A,测量精度(±3~±12)×10-6。3个霍尔电流传感器分别采集电机的三相定子电流信号,通过接口电路对采集的电流信号进行低通滤波、放大和模数转换, DSP读取数据并存储到扩展的存储器中,然后对存储的信号数据进行分析、处理,进而完成故障诊断,从液晶显示器上输出诊断结果。
系统对其中任意一相电流进行故障信息分析、处理,当发现轴承故障时,需要引入另外一相或者两相电流信号作为复核和确认,进而完成故障诊断;系统的有关参数可由PC机设定,通过通信模块传输给DSP;同时,也可将采集的数据信息直接通过通信模块将数据传送到PC机上,兼容离线的故障诊断。
DSP诊断流程:DSP读取外接的24位模数转换器对3路电流传感器采集的数据进行存储后,对采集的数据进行周期图WELCH分析,计算出采集数据的峰度、偏度、波峰因数、间隙、形状因子5个频域特征参数,作为SVM的特征向量,调用SVM诊断子程序,输出轴承故障诊断结果。
2.3 基于SVM的故障诊断
实验的采样频率为10 kHz,分别采集轴承故障定子电流数据和正常电机电流数据50组,采集数据一共100组,每组样本10 000个点。由DSP采集的数据通过通信模块传输给PC机,由PC机对这些信号进行WELCH分析得到定子电流信号的频谱图(见图3),每次分析使用8 192数据点,使用Blackman窗函数,窗长为4 096。

图3 电机WELCH分析频谱对比
由图3可见,由轴承损伤而产生的电流特征频率在故障特征频率fCF=fs±fc、fCF=fs±2fc和fCF=fs±3fc处出现,采用感应电机的定子电流检测法,利用DSP对基于研究的WELCH分析法进行编程,对采样的电流信号进行分析并对感应电机轴承故障特征进行了有效提取。由于此方法提取的故障特征需要依靠人工来识别,无法在线诊断,因此,采用SVM作为故障特征识别的方法,利用2种方法相结合的方式,实现在线诊断。
SVM的训练与参数寻优。将故障电机与正常电机采集的独立的原始数据集D(100组)划分为5个大小相等的互斥子集,将每个子集Di从D中随机分层采样得到,将其中4个子集的并集用作训练集,并将剩余的1个子集用作为测试集。首先对得到的4个训练集进行训练,另外1个子集作为测试集,然后采用上述WELCH分析方法,根据分析结果由公式(8)~(12)计算出峰度、偏度、波峰因数、间隙、形状因子5个参数作为SVM的输入,将故障类别作为SVM的输出,运用交叉验证法进行SVM参数寻优并把最优参数应用于SVM进行训练,得到SVM分类模型。利用该模型对测试集进行评估分类并将分类结果与实际分类进行对比,用准确率、精确率和召回率作为SVM参数寻优的依据。支持向量机的分类精度主要取决于误差惩罚参数C和高斯核函数参数σ的选择,σ由核函数半径γ确定,以上对于不同的C和γ值,重复所述过程,经试验调整,能避免特征数据集的欠拟合与过拟合问题。实验中不同C值和γ值对诊断结果的影响见表1、2,以此作为2个参数优化的依据。
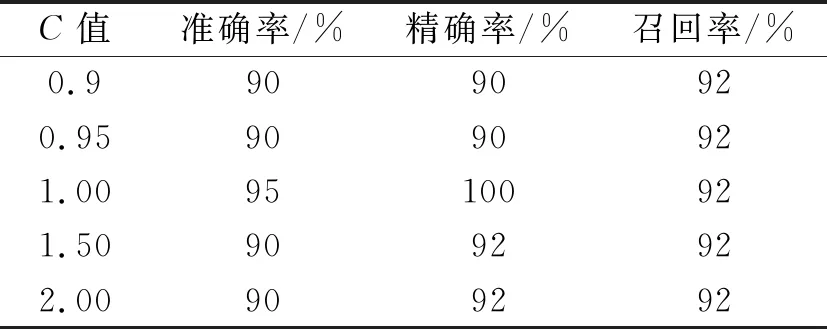
表1 不同C值的SVM诊断结果
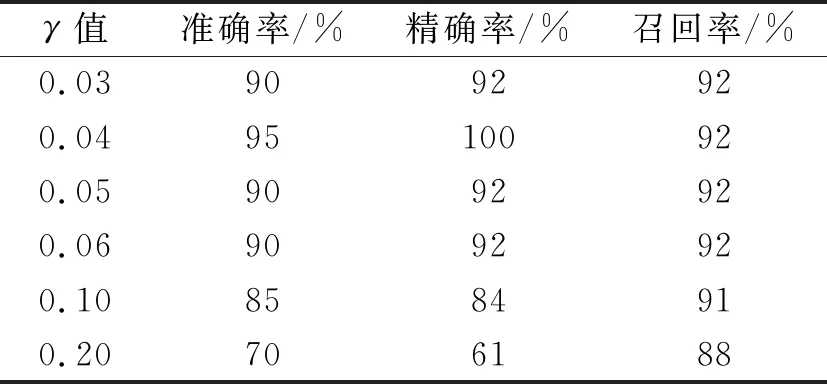
表2 不同γ值的SVM诊断结果
从表1和表2可以看出,C和γ分别采用1.00和0.04的值时,函数对于故障的检测准确率等各项指标均较高。以此对径向基核函数参数的选择和优化,可提高对电机轴承故障检测的识别率和效率。
不同训练样本量的SVM诊断结果见表3,随着样本量的增加,模型分类效果变好,当样本数据达到80组时,模型检测效果基本保持不变,也在DSP系统内存可接受范围内,表明模型在求解小样本数据有一个较好的效果,可满足故障数据不易获得的需求。
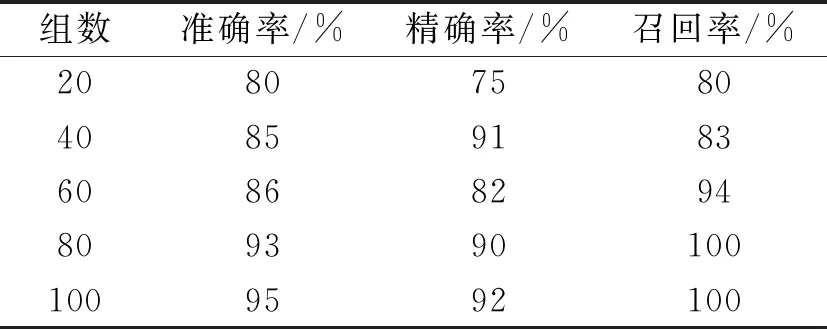
表3 不同训练样本量的SVM诊断结果
采用上述参数寻优得到的分类模型,对新采集的100组数据(轴承故障数据和正常数据各50组)中,随机从故障数据中提取出42组,正常数据提取38组作为训练数据,剩下20组数据作为测试数据,采用交叉验证法的方式进行故障识别。每组提取8 192个数据点进行分析,根据式(8)~(12),计算100 组数据的频域指标参数,形成SVM特征向量,部分计算结果见表4。
系统经优化核函数参数以及经过训练后,对新采集的100组数据的识别诊断结果见表5。
实验结果表明,平均准确率、平均精确率和平均召回率均超过92%,并且这些测试集样本独立于训练集,可满足实际诊断的需要。
3 结论
利用DSP较强的数据处理能力在实验室条件下实现了对感应电机的滚动轴承状态的在线监测。实验结果表明,所提出的方法受船舶环境干扰小,对电机轴承外沟道损伤故障诊断具有良好的识别能力,且具有训练所需故障样本量少,系统成本相对低廉,数据处理、计算相对简单等优点,适合应用于船舶电机轴承故障的在线诊断。

