基于向量式有限元的起重机桁架结构破断过程分析*

杨晓华 刘 龙 马 月 王传存

1 上海振华港机重工有限公司 2 上海海事大学上海离岸工程研究院

1 引言

桁架结构具有自重轻、布置灵活等特点，在建筑、桥梁以及海上工程装备领域得到广泛的应用，其结构安全性也日益引发关注[1,2]。

结构破坏过程中伴随大变形、大位移问题，是复杂的非线性问题。近年来出现的向量式有限元理论[3]，将连续体在空间上离散为一系列质点的集合，在时间上离散为一系列分段的途径单元的集合，并在各时间段内直接用牛顿第二定律取代连续体偏微分方程来描述这些质点的运动，为结构破坏行为研究提供有力的分析思路。该方法能够实现结构倒塌变形的全过程分析，成功应用于建筑、海洋工程等领域。喻莹[4]建立了空间钢结构构件的断裂准则和断裂模式，实现了空间钢结构构件断裂行为的模拟。段元锋等[5]应用分层纤维梁柱单元，计算斜拉桥在地震作用下的结构响应，对其倒塌破坏全过程进行了模拟。基于梁单元理论，朱明亮、郭正兴[6]对大跨度钢结构进行动力学分析。李效民等[7]采用平面弯曲杆件单元计算海洋立管在海流、波浪作用下的动力响应特性。钟杰[8]对框架结构断裂过程进行仿真计算。

针对起重机典型桁架结构应用向量式有限元梁单元理论，进行杆件破断后结构运动全过程分析，分析结构局部和整体的内力和位移变化。

2 向量式有限元梁单元理论

向量式有限元基于点值描述、逆向运动和途径单元概念，将结构的空间形态用点值描述，构成节点和单元；利用单元逆向运动获取纯变形以计算内力；将结构在一时间段内的运动变形划分为多个时间微段的途径单元，每个途径单元都会更新局部坐标系，实现结构位置形状的步步更新。

下面通过三维梁单元描述整个过程。

2.1 点值描述

根据实际结构，向量式有限元将研究对象离散为一系列空间质点，质点具有一定质量，单元不存在质量。

空间梁单元用于分析三维空间结构，节点包括3个平移量和3个转动量，单元内力包括轴力、剪力和弯矩。

由于梁单元没有质量，通过结构单元的质量计算弯曲杆件单元的等效质量和惯性矩。

控制方程是一组由牛顿运动定律得到节点平动和转动微分公式，并运用显式中心差分公式进行求解。

2.2 逆向运动

向量式有限元将质点运动分析的全过程在时间上分为一系列小时间段，每一时段为一途径单元。在途径单元内结构元变形很小，因此每一途径单元的内力增量，包括轴向力，剪力和弯矩，都可以用材料力学公式计算。

在途径单元内，向量式有限元均利用逆向运动求结构变形，逆向运动包括刚体平移与刚体转动。

如图1所示，单元1a-2a经运动变形到达1-2，令其作一个虚拟的平移转动逆向运动，则得到该单元在每一微小时间段内长度转角的纯变形。

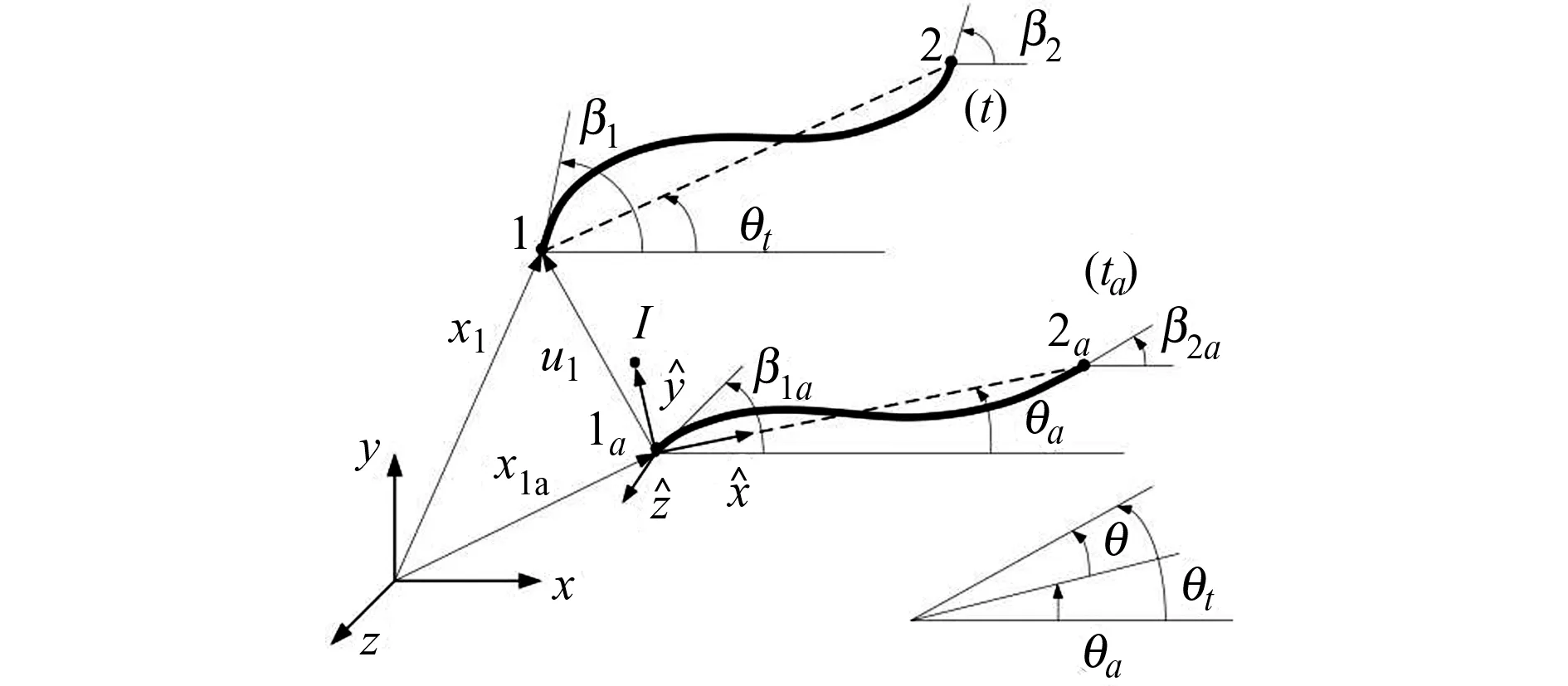
图1 梁单元的运动变形

2.3 单元内力计算

梁单元的变形和内力是根据材料力学的挠曲理论来进行主轴坐标分析，包括长度的变化、轴向的扭力弯曲以及两组弯曲变形，先各自运算，然后矢量相加。对于三维梁单元，计算时还要考虑绕单元主轴的转动。

梁单元节点内力和弯矩：

(1)

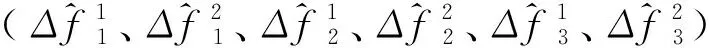
(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

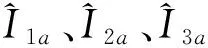
上述内力以全局坐标表示，实际计算时还需转换到构件的局部坐标系中，经过坐标转换和刚体转动后得到节点力。

2.4 计算过程

向量式有限元的计算流程如下：

(1)确定结构的材料、截面性质、阻尼、计算步长及总时长等参数。

(2)将结构划分为节点和梁单元。

(3)通过中央差分控制方程求解节点的运动。

(4)由逆向运动获得单元的纯变形，并确定内力的大小和方向。

(5)更新控制方程中的外力和内力。

(6)判断是否达到计算终止时间。若否，则重复3～5；若是，则输出分析结果。

3 岸桥桁架前大梁破断过程分析

选取某港口岸边集装箱起重机前大梁结构，尺寸见图2。材料为Q345，弹性模量为2.06×1011Pa，泊松比为0.3，密度为7 850 kg/m3，屈服应力为345 MPa。桁架截面为圆管，为简便计算，统一设置圆管外径为0.16 m、内径为0.14 m。

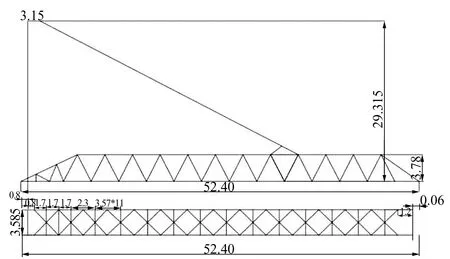
图2 起重机臂架示意图

3.1 模型创建

根据结构尺寸，建立离散化模型，共有102个节点，232个单元(见图3)。

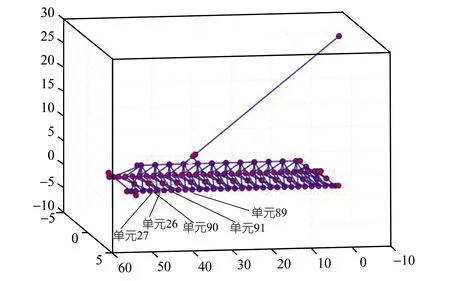
图3 起重机大梁向量式有限元模型

3.2 外载荷施加及约束

在大梁节点施加外载荷，包括起重机额定载重与吊具重量，一共389 158 N，缓慢施加于大梁海侧最远端节点28、61(见图4、5)。

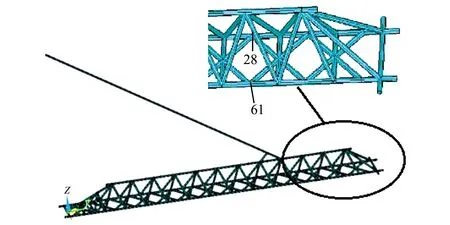
图4 外载施加节点位置

图5 外载荷时程图

根据大梁图纸，在大梁端部和斜拉杆节点处进行固定约束，位于节点2、3、35、36和102(见图6)。

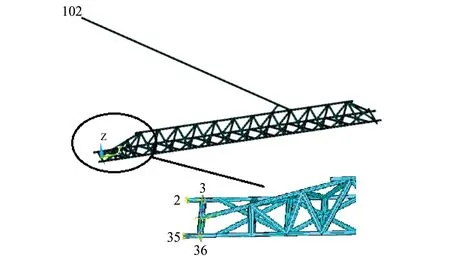
图6 约束节点位置

3.3 三维臂架结构的断裂过程分析

假设臂架在水平位置，单元90在2 s后突然发生断裂。为简化断裂分析计算，假设断裂仅发生在单元两端，同时不考虑单元断裂后的碰撞问题，断裂后脱离结构的单元节点外力只考虑重力。

由图7可以看出，单元90发生断裂后，弯矩和轴力波动较大，然后逐渐趋近于0。图中1、2分别表示单元两个节点。

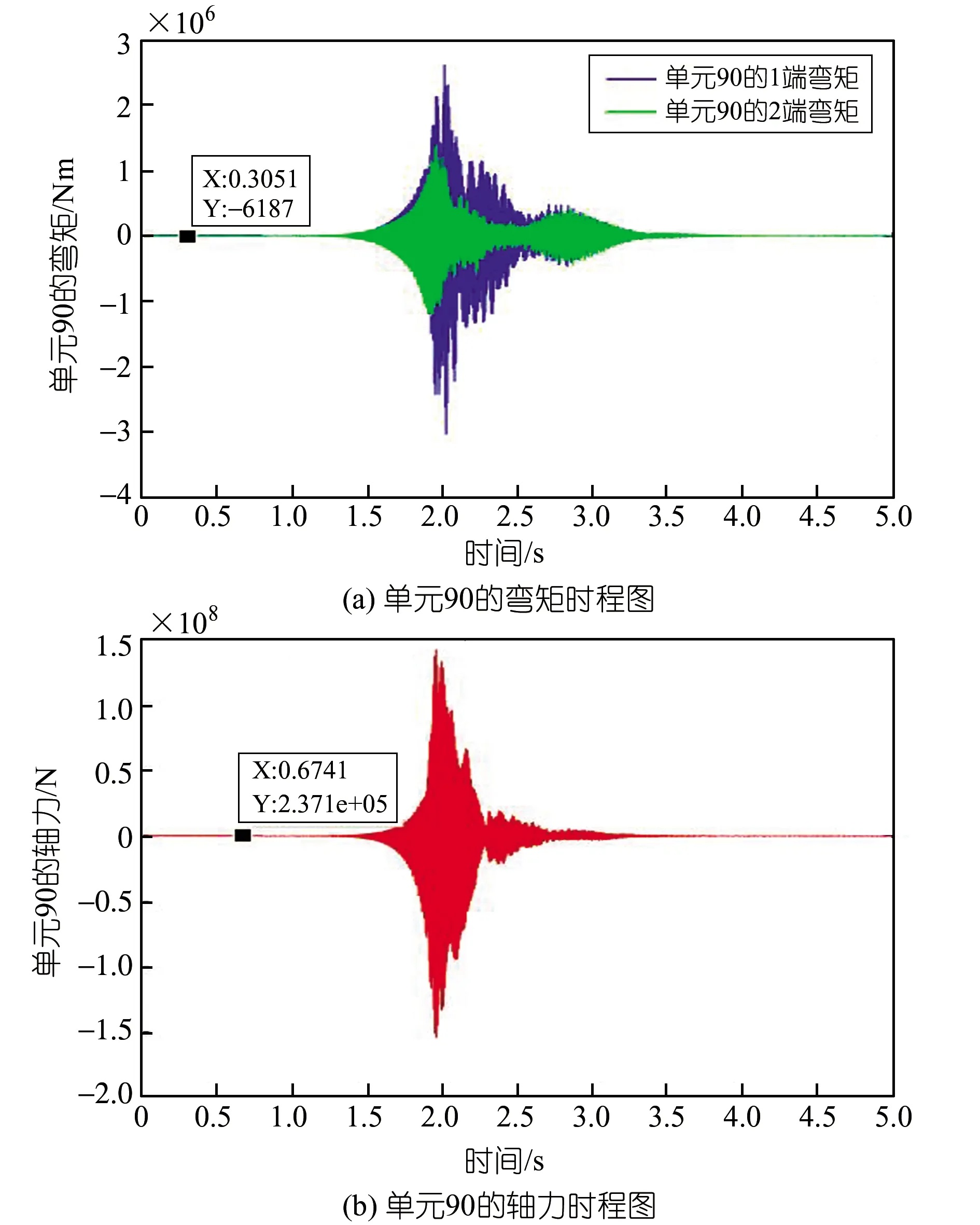
图7 单元90内力变化图

对受载节点局部的单元进行内力分析。单元89与断裂单元90相邻。在发生断裂后，各自形成自由端，弯矩大幅增加，轴力由拉变为压，较断裂前大幅减小(见图8)。

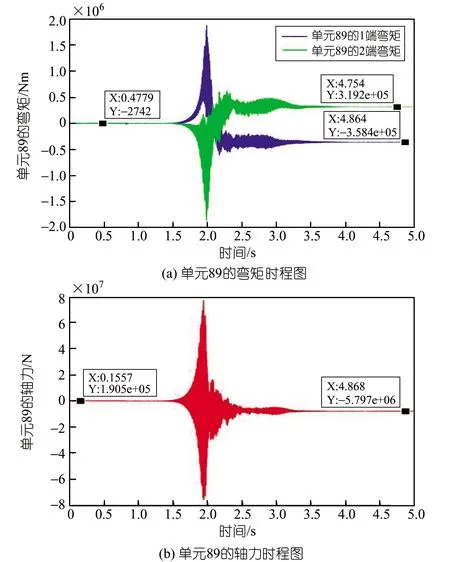
图8 单元89内力变化图

接下来选取外载节点附近的26、27单元进行分析。单元26和27由于靠近受载节点，弯矩变大，轴力增加幅度更大。断裂发生后承受更大的外载(见图9、10)。

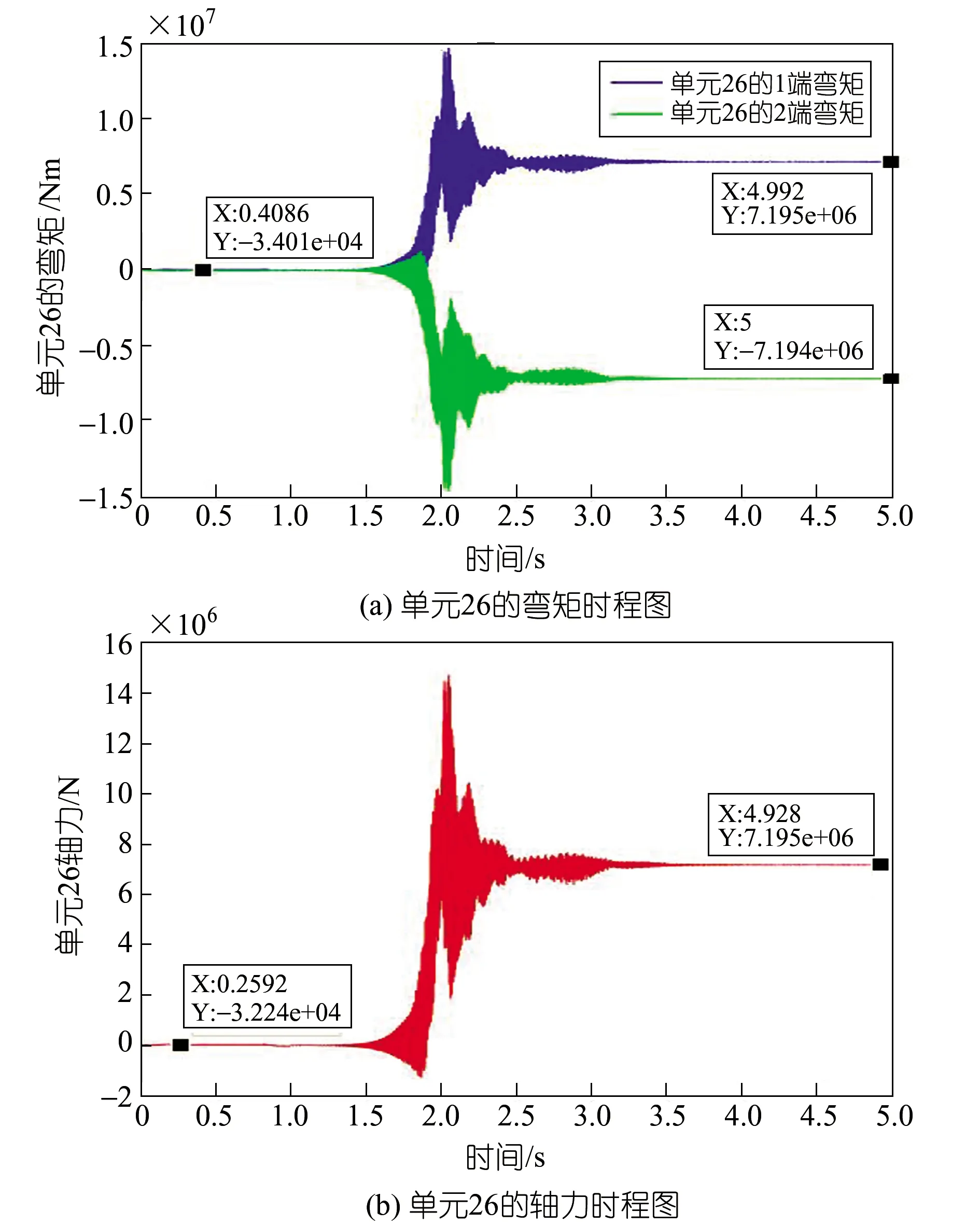
图9 单元26内力变化图

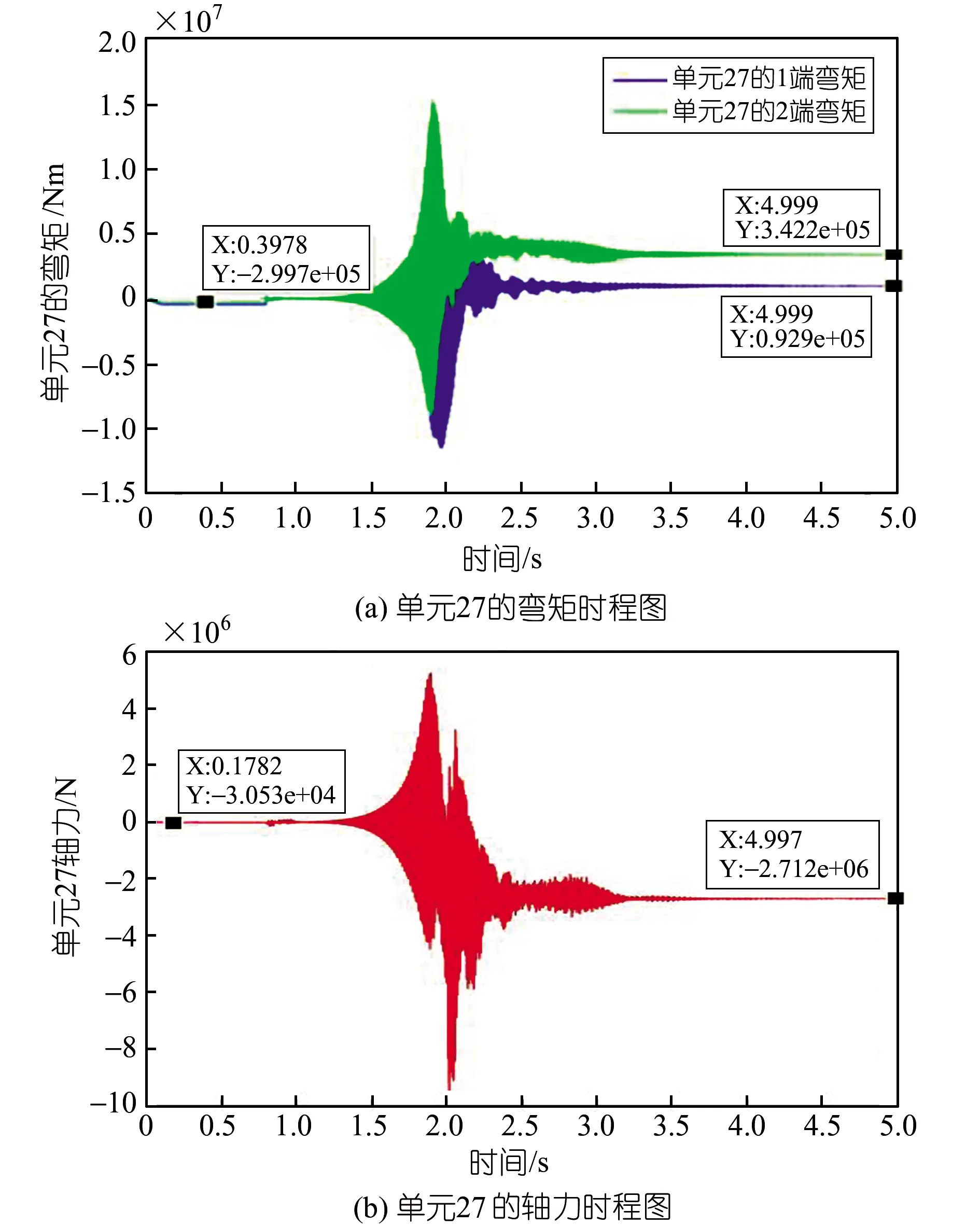
图10 单元27内力变化图

4 结语

基于向量式有限元梁单元理论对起重机臂架结构进行破断过程分析，展示了某一个单元发生断裂后局部结构到整体结构的内力变化，为研究起重机大型钢结构倒塌演变机理、探索倒塌模式控制奠定了基础，为结构倒塌分析提供了新的思路，为结构安全设计提供参考。本研究主要考虑结构强度安全，没有考虑构件失稳、碰撞等破坏形式，对此有待进一步深入研究。