全局方向模板对非结构有限体积梯度与高阶导数重构的影响1)
孔令发 董义道 刘伟
(国防科技大学空天科学学院,长沙 410073)
引言
非结构网格是CFD 数值模拟较常用的一类网格,其生成方便快捷,能够在较少的人为干预下自动生成[1-2],这大幅度缩减了网格的生成周期;同时非结构网格具备较高的灵活性,其能快速高效地处理网格运动、网格变形以及网格加密等问题,并对不同外形具有较强的适应性[3-4].因此,相比多块结构化网格,非结构网格的使用带来了极大的便利.但当前制约非结构网格在复杂外形上应用的主要原因是,其很难保证计算效率与求解精度[5-7].因此,为了充分利用非结构网格自动化的生成能力,学者们不断尝试改进离散算法来突破精度损失以及稳定性恶化的瓶颈,实现网格生成自动化和数值模拟精准化的统一.
当前常用的非结构网格算法是二阶精度有限体积方法[8-13],该方法被用于很多知名软件与程序库,如:Ansys’s Fluent(http://www.ansys.com),以及开源软件OpenFOAM (http://openfoam.org) 等[14-17].在众多不同的有限体积离散方法中,单元中心型[8-9,12]的非结构有限体积方法应用最为广泛,该方法的离散过程相比单元顶点型更加简便[18-19].但不论对于单元中心型还是单元顶点型的有限体积离散方法,梯度重构是影响求解器求解精度的重要过程[20-24].对于二阶精度有限体积方法,目前较为常见的梯度重构方法包括格林高斯与最小二乘方法两类[16].但为了提高计算效率与对流场的分辨率,一些学者尝试将非结构有限体积方法向高精度推广.关于高精度非结构有限体积算法的构造,Barth 等[25-26]基于最小二乘方法,构造了k-exact 重构算法.此后,Olliver-Gooch[27-33]基于k-exact 重构,发展了一系列高精度非结构有限体积离散方法.一般而言,随着重构精度的增加,所需要的网格单元数量,即模板个数也会随之增多,并且采用不同的模板选择方法,对梯度与高阶导数重构乃至最终流场计算结果会产生重要影响.
考虑到非结构网格不具备结构网格的笛卡尔索弓,所以在梯度重构的过程中只能依赖于一定的准则来寻找模板单元[34].目前较为常用的模板选择方法是选择与中心单元共面或共点的网格单元来构建模板集合.这两种模板的数量可控,但选择方式均依赖于固定的网格拓扑关系,无法在模板选择过程中体现出流动的变化特征.如边界层流动,该流动沿着壁面法向的变化剧烈,因此在重构过程中,我们更希望模板单元能够尽可能多地体现沿壁面法向的流动信息.考虑到这个因素,2018 年Xiong 等[35]提出了基于局部方向的模板选择方法,该方法在各向同性以及压缩比较小的三角形网格上可近似沿着壁面法向与切向来扩充网格单元,能够较为准确地反映流场变化,并且模板单元的扩充严格依赖于两个局部方向,具备类似于结构网格沿着i,j两个索弓方向求解的特点,并试图通过弓入这种结构化特性[34]来改善基于非结构网格算法的数值表现.经过分析,这种模板选择方式虽然初步考虑了流场的特征,但其单元局部方向的确定严格依赖于阵面推进过程(advancing front technique)[36-37],该过程在方向判断时较为复杂.其次,在高度各向异性的三角形网格上,基于此方法找到的模板单元与壁面法向间的偏差较大,这将对梯度重构以及流场计算过程产生不利影响.
基于局部方向模板存在的问题,在前期的工作中,针对二阶精度有限体积方法探索了一种新的模板选择方法,并将其命名为全局方向模板.该方法不再依赖于每个网格单元独立的局部方向,而是求解域的两个全局方向,即壁面法向与切向,并且模板单元严格沿着全局方向依次扩充.该方法的优势在于,找到的模板单元均沿着两个相互垂直的全局方向,其空间延展性较好,具备更加明显的结构化特征[34].更重要的是,全局方向模板选择方法不再依赖于网格拓扑约束,即使在大压缩比三角形网格上也能够较为准确地反映流动的各向异性.此外,相比局部方向模板选择方法,该方法更为简便,避免了复杂的阵面推进与方向判断过程.经算例验证,采用全局方向模板得到的计算误差相比局部方向模板更低,并且也接近甚至低于常用的共点模板.
为了进一步验证全局方向模板在高阶精度有限体积方法中应用的可行性,在此工作中,我们将初步测试采用全局方向模板对梯度以及高阶导数重构准确性的影响.文章的总体结构如下:第1 节主要介绍了高阶精度非结构有限体积离散方法以及k-exact 重构算法的基本过程;第2 节回顾了几种常用的模板选择方式,包括共点模板、共面模板,同时重述与分析了局部方向模板选择方法的基本思路,并给出全局方向模板选择方法的具体过程和在各向异性三角形网格上的表现效果;在文章的第3 节,为了验证全局方向模板在高阶精度有限体积方法上应用的可行性,我们在不同大压缩比三角形网格上设置典型数值算例,来比较几种不同模板对梯度与高阶导数重构精度及准确性的影响,并在此基础上对比了由不同模板得到的高斯点处的变量点值与导数误差; 第4 节给出了本文结论与下一步工作展望.
为验证全局方向模板在高阶精度有限体积方法上应用的可行性,本文初步测试了该模板对变量梯度以及高阶导数重构的影响,以期为高精度非结构有限体积离散提供一种更为简单有效的模板选择方式.
1 非结构有限体积方法
1.1 控制方程及其离散
针对无黏流动,积分型欧拉控制方程为
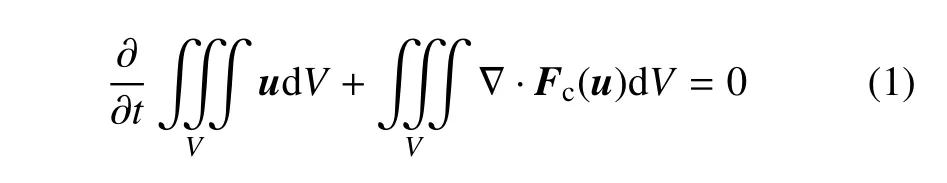
基于高斯积分公式,可将方程(1)中的散度体积分转化为环面积分

式中,u为守恒变量,Fc(u) 为对流通量,n为控制体边界面外法向矢量,V与∂V分别代表积分域与积分域边界.对于高阶有限体积方法,该控制方程可被离散为

对于控制体i,Nf代表单元面数量.由于高阶有限体积离散时,仅构造单元面中心点处的通量无法达到二阶以上精度,因此在每个单元面处随着精度要求的不同,所需要的高斯积分点的数量也不同.NG代表当前单元面处高斯积分点的数量,ωk与Φjk分别为每个高斯积分点处的权系数与数值通量,nj与S j为单元面处的单位外法矢量与单元面面积(二维时为单元边长).图1 给出了有限体积离散与通量构造的基本过程.
如图1 所示,为采用近似黎曼方法[30-31]构造单元面某高斯积分点处的数值通量,需要首先构造单元面处的左右状态矢量.

图1 非结构有限体积离散与通量构造示意图Fig.1 Unstructured finite volume discretization and flux construction

式中,与分别代表当前时间步高斯积分点处的左右状态矢量,xG,yG;xi,yi与xj,yj分别代表高斯积分点以及单元i与单元j的中心点坐标值.在得到左右状态矢量的基础上,可采用Roe 格式[38-39]构造数值通量,其基本表达式如下

1.2 k-exact 重构算法
由于本文研究全局方向模板在高阶精度非结构有限体积方法中的应用,因此采用k-exact 方法来实现梯度与高阶导数重构.此过程需要利用中心控制体单元i的模板单元来构造重构函数Ri(x-xi),其包含单元i的平均值,并且任意多项式都可被函数Ri(x-xi)在不大于k阶精度的条件下精确重构,即

但在重构过程中,为达到重构精度,始终需保证重构函数与待重构变量在控制体单元上的几何平均值相等
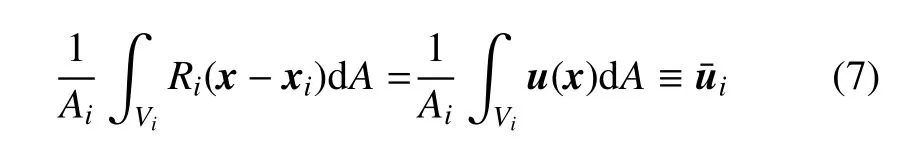
式中V代表控制体.对于k-exact 重构,其重构函数的形式为
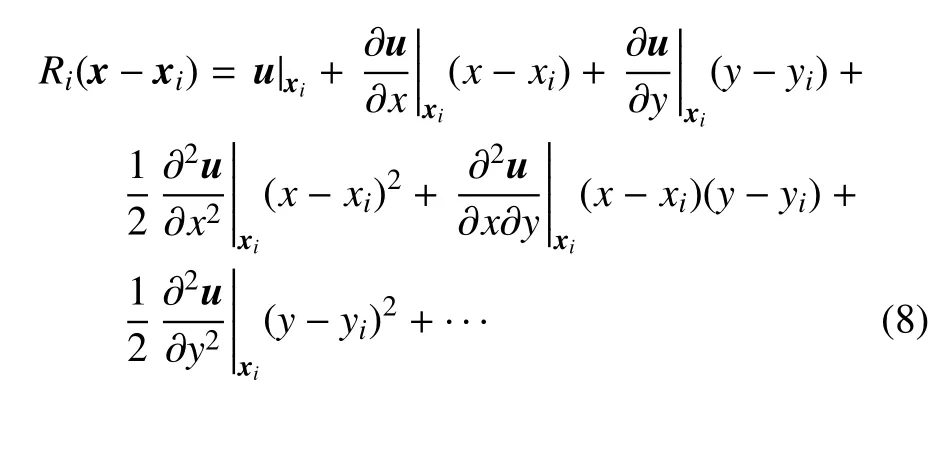
将方程(8)等式两边同时在控制体单元i上积分可得

式中,为几何量在控制体上的体积分,Ollivier-Gooch 在文献[32]中将其命名为Moments,该积分量的具体表达式为

在此基础上,将重构函数Ri(x-xi)在单元j(即中心单元i的模板单元上积分可得

经简化,方程(11)最终可表示为


参照方程(12),对于任意模板单元j,均可构造一个重构多项式,现将所有多项式整合可得到如方程(14)所示地矩阵方程组,通过求解该方程组,便可得到单元i的变量梯度及其高阶导数

式中每一个重构方程前面都乘以权系数ωij
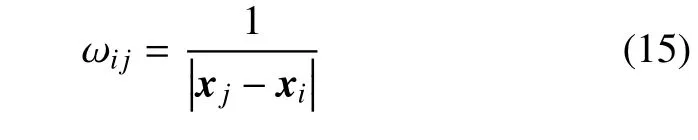
该系数采用参考点之间距离倒数的形式,用来强调距离中心单元较近的模板单元对重构结果的影响.
2 模板选择方法
首先介绍了两种常用的模板选择方法,其次讨论了基于局部方向的模板选择方法,并在大压缩比三角形网格上分析了这种模板存在的问题.最后,在局部方向模板缺陷的基础上,给出了全局方向模板在不同压缩比三角形网格上的表现效果,以进一步突显全局方向模板的优势.
2.1 两种常用的模板选择方法
较常用的模板选择方式有两种,分别为共面模板与共点模板.顾名思义,共面模板由与中心单元共单元面的网格单元组成,共点模板则由所有与中心单元共顶点的网格单元组成.如图2 所示,两种方法的模板单元数量由模板层数控制.如对于共点模板,其第一层模板是所有与中心单元共顶点的网格单元,而第二层模板则是所有与第一层模板共顶点的网格单元.
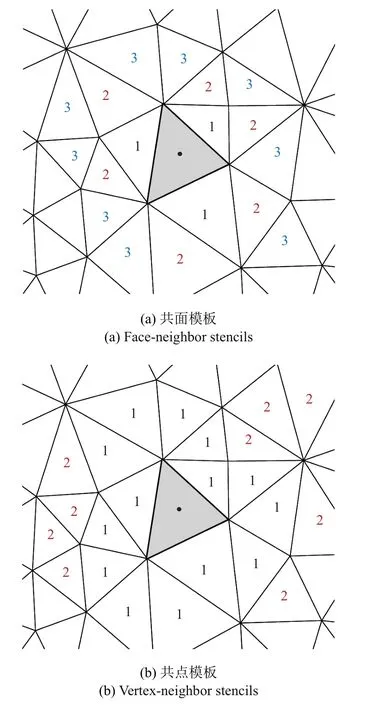
图2 共面与共点模板Fig.2 Face-neighbor and vertex-neighbor stencils
如图所示,共点与共面模板均依赖于固定的网格拓扑关系,针对不同流动,这两种模板选择方式无法较好反映流场特性,例如边界层型流动所表现出的流动各向异性.
2.2 局部方向模板选择方法
针对上述两种模板选择方式存在的问题,Xiong等[35]在2018 年提出了一种具有分维特征的结构化模板构造方法.所谓结构化[34],是指模板选择沿着两个相互垂直的方向进行.其次在确定局部方向的过程中,能够尽量保证找到的两个局部方向沿着壁面法向与流向,以此来捕捉流动的变化.

图3 三角形单元局部方向的可能组合方式Fig.3 Possible combinations of local directions on triangular cell
对于局部方向的确定,首先要将网格单元分为四边形与三角形两种情况来考虑.如图3 所示,如果网格单元是四边形,两个局部方向则为两组对边中点的连线;但三角形单元由于不存在两组对边,因此Xiong 等[35]将三角形的其中一个顶点视作由四边形的一条边退化而成,并将这个点称为三角形单元的退化点.进而三角形网格单元的局部方向由退化点与对边中点的连线(其被命名为第一局部方向),以及另外两条边中点的连线(第二局部方向)组成.从图3 可以看出,对于一个三角形单元而言,其退化点的位置有三种不同的可能性,因此三角形网格单元的局部方向也存在三种可能的组合方式.
采用阵面推进技术[36-37]可最终确定退化点的位置以及局部方向的最终组合方式,由于其过程繁琐,在此不再阐述.经过阵面推进后,可以找到所有网格单元的局部方向组合,如图4 所示.图中黑色线段代表三角形网格单元及壁面,红色线段表示单元内的局部方向.
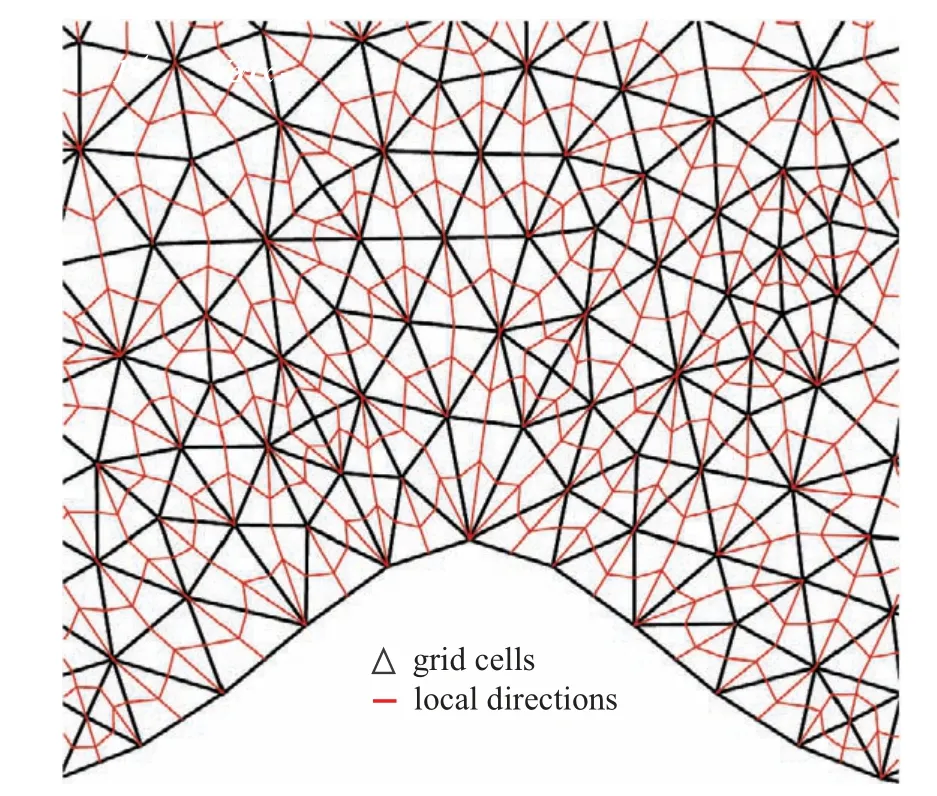
图4 三角形网格单元的局部方向Fig.4 Local directions of triangular cell
在确定所有单元局部方向的基础上,可沿着两个局部方向来扩充模板单元.但对于三角形单元,沿着局部方向确定模板单元还需要分为按点寻找与按边寻找两类,该过程涉及局部方向的传递与夹角的判断,由于较为繁琐,本文不再重述其详细判断规则,具体过程见文献[35].
图5 展示的是在不同网格压缩比的三角形网格上沿局部方向找到的模板单元效果.如图5(a)所示,当网格压缩较小时,第一局部方向接近壁面法向,沿着两个局部方向找到的模板单元体现出结构化分维特征;此外,模板的空间延展性更好,能够较为准确地反映流场变化.但该方法仍存在一些问题,如图5(b)所示,当网格压缩比较大时,模板呈现“畸形”现象.
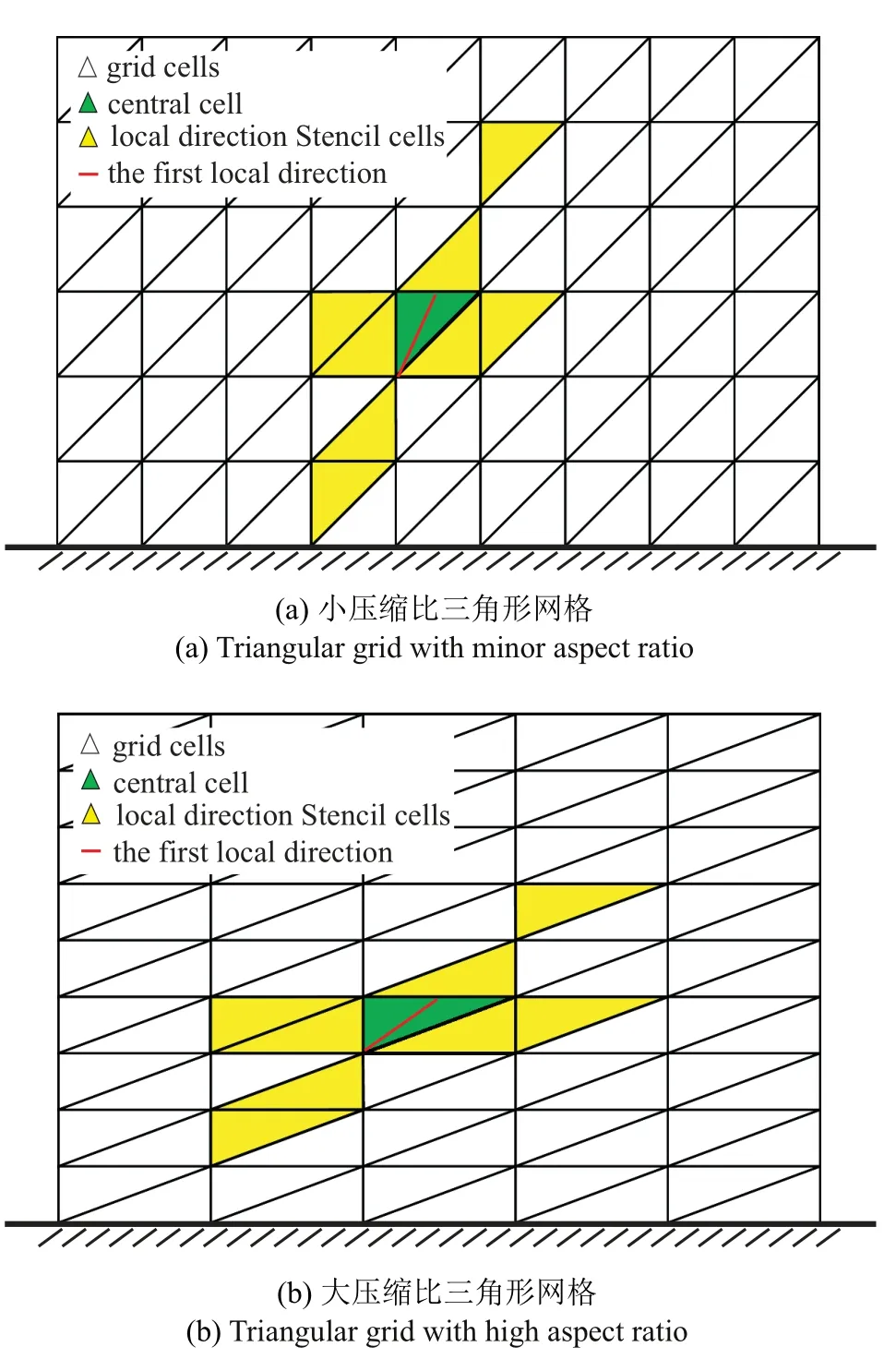
图5 在不同压缩比三角形网格上的局部方向模板Fig.5 Local-direction stencil cells on triangular grids with different aspect ratios
出现这一问题的原因在于针对高度各项异性的大压缩比三角形网格,基于“阵面推进”方法得到的局部方向严重偏离壁面法向,并且两个局部方向之间的夹角较小,导致模板在空间的延展性较差,无法正确反映局部流动变化.
鉴于上述局部方向模板存在的问题,迫切需要发展一种新的模板选择方式,并具备能脱离网格拓扑约束与准确反映流动变化特征的能力.
2.3 全局方向模板选择方法
2.1 与2.2 节回顾了两种常用的模板选择方法以及局部方向模板的基本思路,讨论了其在不同网格上的表现效果.经分析,局部方向模板虽体现了结构化特征,在压缩比较小的三角形网格上能够较为准确地反映流场变化,但随着网格压缩比的增大,其第一局部方向逐渐偏离壁面法向,导致方向性的失效.据此,在之前的工作中,我们设计了一种基于全局方向的模板选择方式,并将其应用于二阶精度非结构有限体积方法.所谓全局方向,是指对于边界层型各向异性流动,首先可以确定两个特征方向,其中一个方向沿着壁面法向,也就是流场变化剧烈的方向,通常沿该方向的网格尺度较小; 另外一个方向沿着流向,对应的网格尺度较大.所有的模板单元均沿着两个全局方向依次扩充,因此避免了局部方向模板选择方法中的阵面推进过程,并且具备准确反映流场特征的能力.
具体而言,首先对于控制体单元,过单元中心作两条平行于壁面法向与切向的直线,其次在给定的单元集合中找到与两条直线相交的网格单元来构建新的模板.通常,该单元集合由与中心单元共点的网格单元构成.图6 所反映的是全局方向模板在不同压缩比网格上的效果,图中红色与黑色虚线分别代表全局方向以及网格边界面法向,绿色、蓝色、橙色以及黄色的网格单元分别代表中心单元、第一层与第二层共点单元,以及全局方向模板单元.如图6 所示,所有的模板单元均沿着两个正交的方向,更加直观地体现出结构化分维特征;其次,不论网格是否存在大压缩比,全局方向模板始终沿着壁面法向与切向.因此,相比局部方向模板,全局方向模板可更加准确地准确捕捉到流动的各向异性特征.
根据图中所反映的现象可以看出,基于该方法确定的模板单元能够更加准确地反映流场特征,并且随着共点单元层数的增加,模板单元沿两个全局方向依次增加,因此模板数量可得到较为准确的控制.此外,经算例验证,采用全局方向模板可有效提高二阶精度非结构有限体积方法的计算准确性.为了进一步推广全局方向模板在高精度方法中的应用,在下一节我们将通过典型的数值算例来初步检验该模板对变量梯度及高阶导数重构的影响.

图6 在不同压缩比三角形网格下的全局方向模板Fig.6 Global-direction stencil cells on triangular grids with different aspect ratios
3 梯度和高阶导数重构精度测试
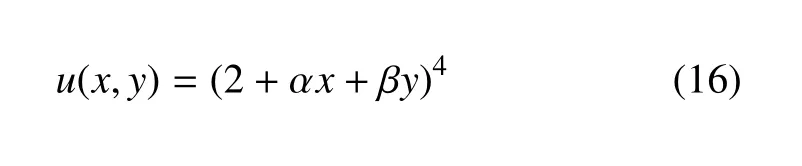
为了检验全局方向模板在高阶精度非结构有限体积方法中的数值表现,本节在不同压缩比的三角形网格上设置了一个典型的数值算例[33]来检验采用该模板得到的变量梯度与高阶导数的重构准确性,并将其与局部方向模板以及共点模板的重构效果对照,进而验证新模板选择方法的有效性,及其在高精度方法中应用并推广的可行性.待测函数的形式如下该函数连续可导,且给定的求解域范围是x,y∈[-0.5,0.5]×[-5e-AR,5e-AR],其中AR表示网格的压缩比,α 与β 为两个实数,其之间的关系为:β/α=AR.在网格压缩比较大时,此函数沿着y方向(对于直线边界网格即壁面法向)的变化剧烈,而在大压缩比情况下,沿着x方向变化较小,这种变化特征与边界层型流动所表现出的现象相似.
此外,采用的计算网格为由背景四边形剖分得到的三角形网格.为了体现非结构网格的随机特性,并降低计算对网格的要求,如图7 所示,我们分别测试了规则剖分与随机剖分两种网格拓扑,并对两种拓扑下的规则网格添加随机扰动,以充分对比不同模板的计算效果差异.
为更加直观地体现在高度各向异性网格下,不同模板对梯度与高阶导数重构的影响,文章中给出了压缩比AR=103时由4 种网格分别得到的计算结果,并在每种网格拓扑下,设置了由疏到密的5 套网格.5 套疏密程度不同的背景四边形网格在x与y方向网格量的分布如表1 所示.


图7 计算网格示意图Fig.7 Schematic diagram of computational grids

表1 背景四边形网格的网格量分布Table 1 The distribution of background quadrilateral grids
对于高阶精度非结构有限体积方法,重构过程的待求量除变量梯度外,还有其高阶导数.本算例测试了在三阶精度下的重构效果,并采用变量梯度以及高阶导数的L2误差(平均误差) 来进行误差收敛性分析.算例的解析解已知,通过对函数(16)求导可得
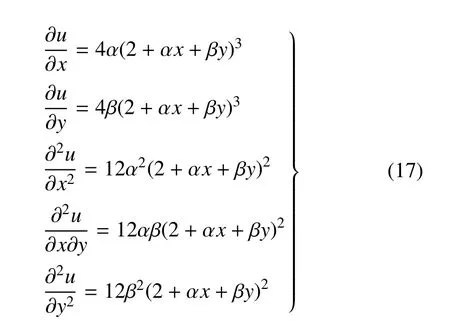
考虑到重构单元梯度与高阶导数的最终目的是计算单元面高斯积分点处的变量点值与导数值,以构造对流通量与黏性通量.因此,本节在测试单元梯度与高阶导数的基础上,为了进一步验证不同模板的重构结果对实际计算的影响,还分别统计了在不同网格上,单元面高斯积分点处的变量点值与导数误差.
计算变量点值与导数时,由单元中心插值到高斯积分点即可,如公式(18)所示

式中,下标Gk与下标i分别代表高斯点与单元中心.
3.1 规则网格下的数值计算结果
图8 和图9 给出的计算结果分别代表在规则网格上,使用3 种模板得到的两个一阶导数∂u/∂x,∂u/∂y,以及高阶导数∂2u/∂x2,∂2u/∂x∂y和∂2u/∂y2的L2误差.如果该函数的解具有三阶精度,则其一阶导数(即梯度) 应具备二阶精度,二阶导数应具有一阶精度.同时,在图表中为简化对不同模板的描述,使用V-Stencil、L-Stencil 以及G-Stencil 来分别表示共点模板、局部方向模板以及全局方向模板,Slope2 与Slope1 代表二阶与一阶精度标准线.此外,表2 所列举的数据为:在规则密网格上,由3 种模板得到的梯度以及高阶导数L2误差的具体数值.
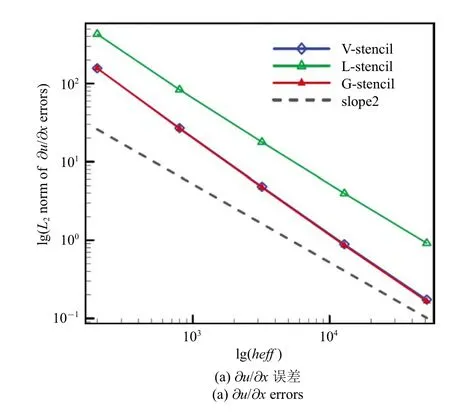

图8 规则网格梯度L2 误差Fig.8 L2 norm of gradient errors on regular grids
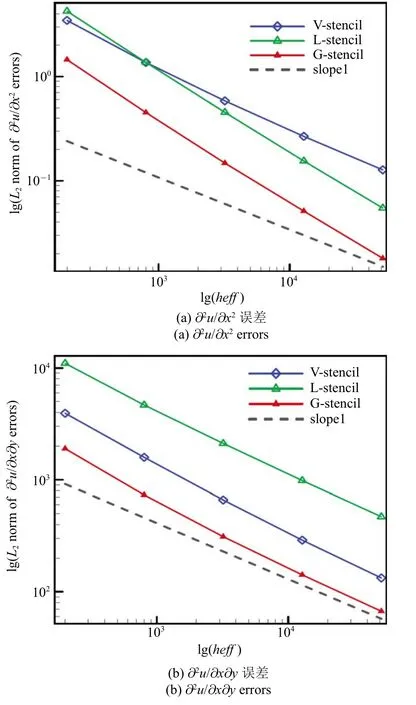
图9 规则网格上高阶导数的L2 误差Fig.9 L2 norm of high-order derivative errors on regular grids
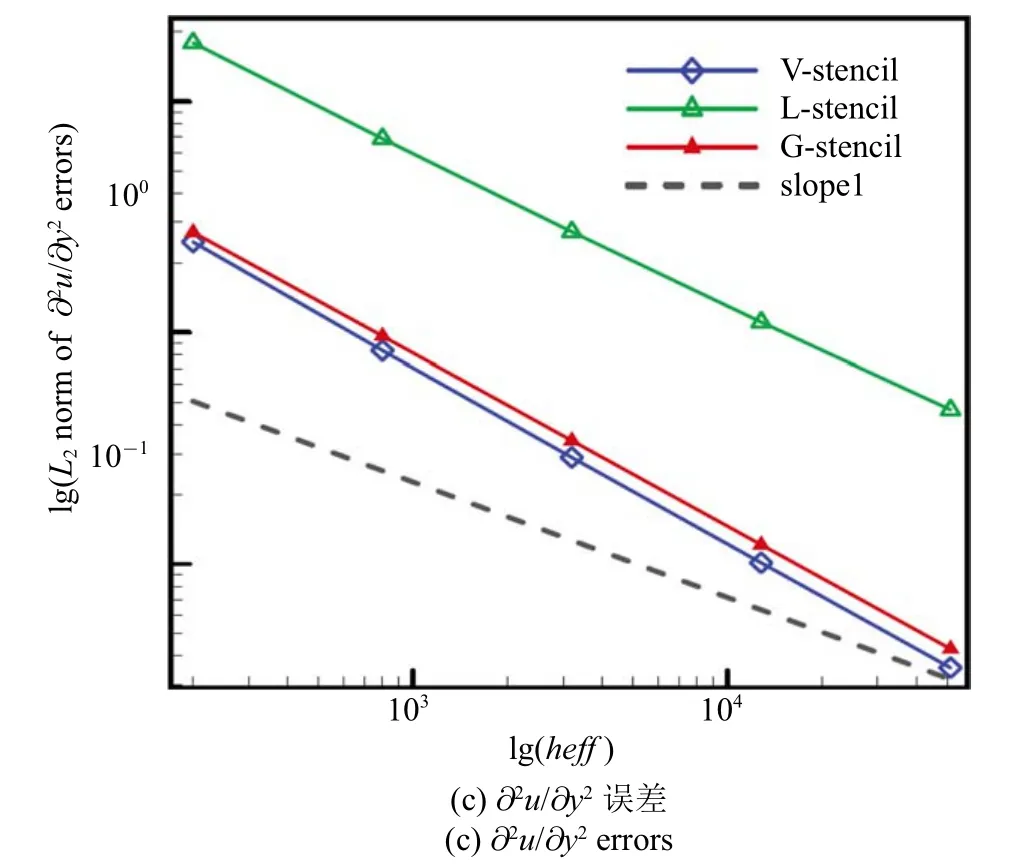
图9 规则网格上高阶导数的L2 误差(续)Fig.9 L2 norm of high-order derivative errors on regular grids(continued)

表2 密网格上梯度与高阶导数的L2 误差Table 2 L2 errors of derivatives on the vfin grid
从图8 反映的结果可以看出,3 种模板选择方法下梯度的计算结果均达到了设计精度,并且采用全局方向模板得到的∂u/∂x与∂u/∂y误差与共点模板接近.然而局部方向模板的数值表现较差,采用该模板选择方法得到的计算误差在3 种方法中最高.此外,我们统计了高阶导数的重构误差,其结果如下.
从图9 可以看出,局部方向模板的计算误差在3种方法中偏高,∂2u/∂x∂y和∂2u/∂y2两项与常用的共点模板差距较大.此外,结合表2 中的数据可以看出,全局方向模板的∂2u/∂y2误差与共点模板接近,但稍高于共点模板,而∂2u/∂x2与∂2u/∂x∂y误差在3 种模板中最低.因此,当采用规则剖分的三角形网格时,全局方向模板在梯度与高阶导数重构方面具有较好的数值表现.
此外,为了进一步检验重构结果对实际计算的影响,我们统计了高斯积分点处的变量导数与点值误差.统计结果如图10、图11 以及表3 所示.

图10 高斯积分点处梯度L2 误差Fig.10 L2 norm of gradient errors at Gauss point

图11 高斯积分点变量点值L2 误差Fig.11 L2 norm of variable errors at Gauss point

表3 密网格上高斯点处的变量点值与导数的L2 误差Table 3 L2 errors of variable and derivatives at Gauss points
从图10 与图11 以及表3 可以看出,在高斯积分点处,采用全局方向模板得到的变量导数与点值误差与共点模板接近,但均低于局部方向模板.因此,全局方向模板对单元梯度与高阶导数重构的优势,在高斯积分点处得到了较好地验证.
3.2 扰动网格下的数值计算结果
在规则三角形网格的基础上,我们对其添加随机节点扰动,以测试不同模板对随机扰动网格的适应性.图12 与图13 分别列举了梯度与高阶导数的L2误差.
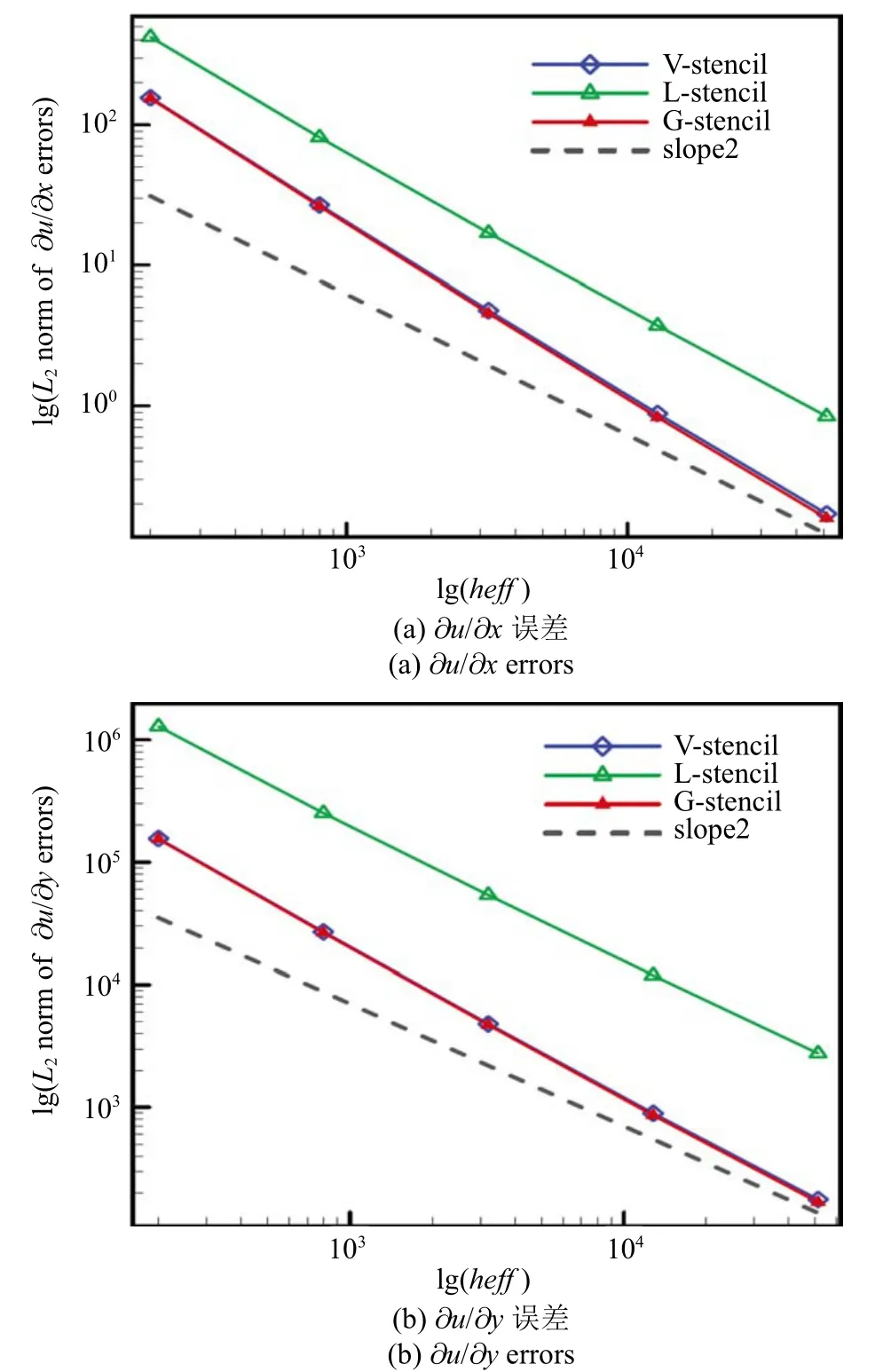
图12 扰动网格梯度L2 误差Fig.12 L2 norm of gradient errors on perturbed grids
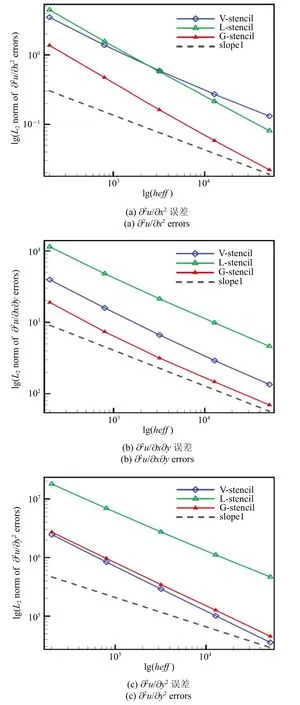
图13 扰动网格上高阶导数的L2 误差Fig.13 L2 norm of high-order derivative errors on perturbed grids
从图12 的结果可以看出,由全局方向模板得到的梯度误差明显低于局部方向模板,并且与共点模板的计算结果接近.此外,高阶导数的重构结果如下.
从图13 可以看出,在扰动网格上高阶导数的误差变化规律与规则网格相似,全局方向模板对三个高阶导数的重构均有较好的数值表现.此外,高斯积分点处的变量导数与点值误差统计结果如图14 和图15 所示.

图14 高斯积分点处梯度L2 误差Fig.14 L2 norm of gradient errors at Gauss point
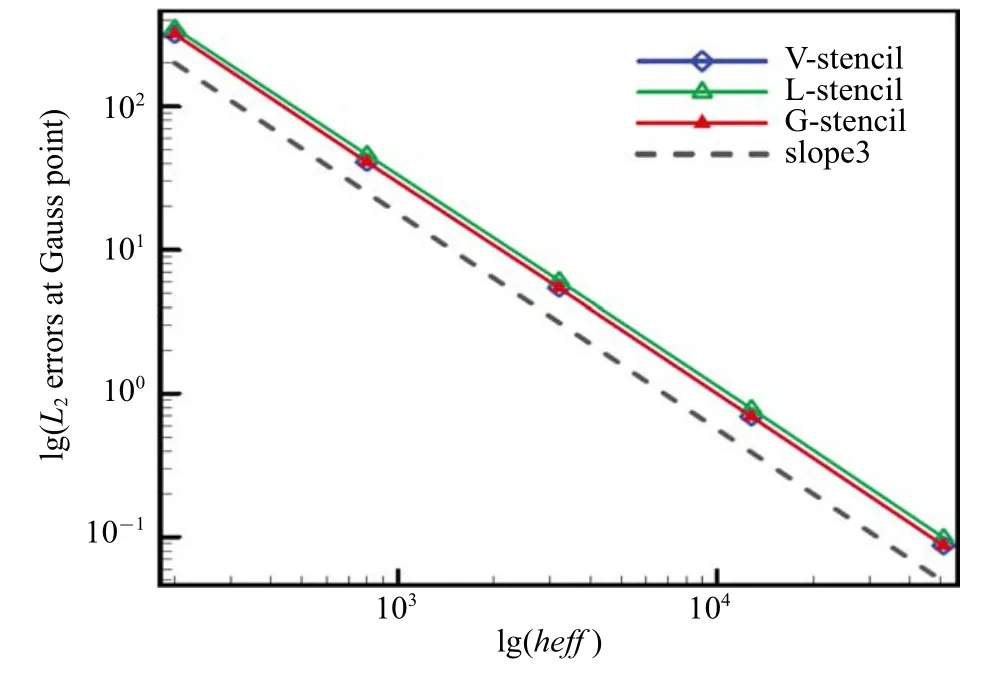
图15 高斯积分点变量点值L2 误差Fig.15 L2 norm of variable errors at Gauss point
从图中可以看出,当网格存在扰动时,高斯积分点处的误差变化规律同样与规则网格接近.此外,结合对单元梯度与高阶导数的重构结果,可以充分说明全局方向模板对扰动网格同样具有较好的适应性.
3.3 随机剖分扰动网格下的数值计算结果
从3.2 节可以看出,对网格添加随机节点扰动后,误差的变化规律与规则网格相似.为简化结果分析,本节给出了对随机剖分网格添加节点扰动后的数值结果.图16 与图17 分别给出了梯度与高阶导数的L2误差.表4 中列出的数据为密网格上,各阶导数的具体误差值.
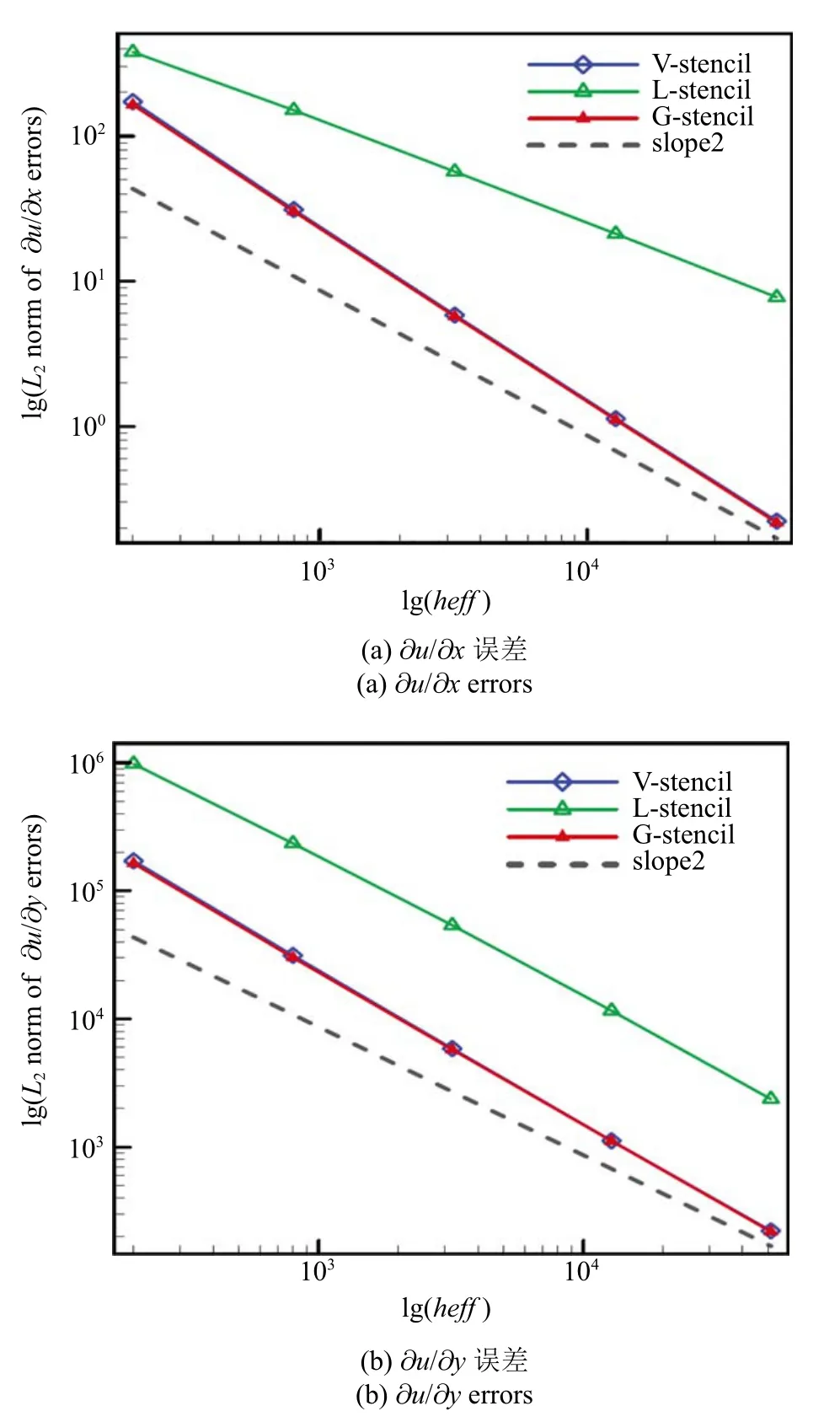
图16 随机剖分扰动网格梯度L2 误差Fig.16 L2 norm of gradient errors on randomly-diag perturbed grids

图17 随机剖分扰动网格上高阶导数的L2 误差Fig.17 L2 norm of high-order derivative errors on randomly-diag perturbed grids
从图中反映的结果可以明显看出,由全局方向模板得到的两个一阶导数均达到了二阶精度,但由局部方向模板得到的∂u/∂x项的计算精度低于上述两种模板,并且其计算误差明显偏高.在此基础上,还统计了高阶导数的重构误差.

表4 密网格上梯度与高阶导数的L2 误差Table 4 L2 errors of derivatives on the vfin grid
从图 17 可以看出,由全局方向模板得到的∂2u/∂y2与共点模板接近,并稍高于共点模板,而∂2u/∂x2与∂2u/∂x∂y误差在3 种模板中最低.此外,从2.3 节对全局方向模板的描述以及图6 中可以看出,相比共点模板,全局方向模板可有效减少用于重构过程的模板数量.因此,该模板的使用不仅显著改善了高阶精度非结构有限体积方法的计算准确性,而且可提高计算效率.
为检验在当前网格拓扑上,不同模板的单元梯度与高阶导数重构结果对实际计算的影响,我们同样统计了高斯积分点处变量导数与点值误差,统计结果如图18 和图19 所示.此外,表5 中列出的数据为3 种模板在密网格上的具体误差值.
从统计结果来看,由全局方向模板得到的高斯点处的变量导数与点值误差与共点模板接近,并稍低于共点模板.因此,全局方向模板对梯度与高阶导数重构的优势得到了较好地验证.
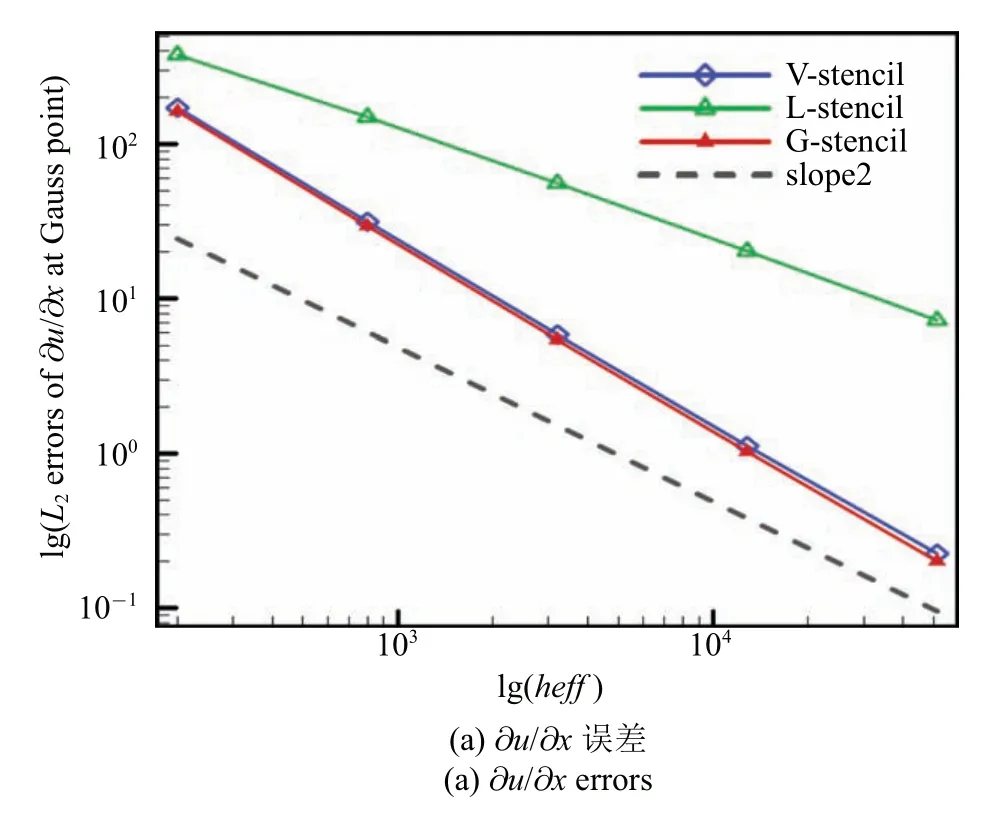
图18 高斯积分点处梯度L2 误差Fig.18 L2 norm of gradient errors at Gauss point
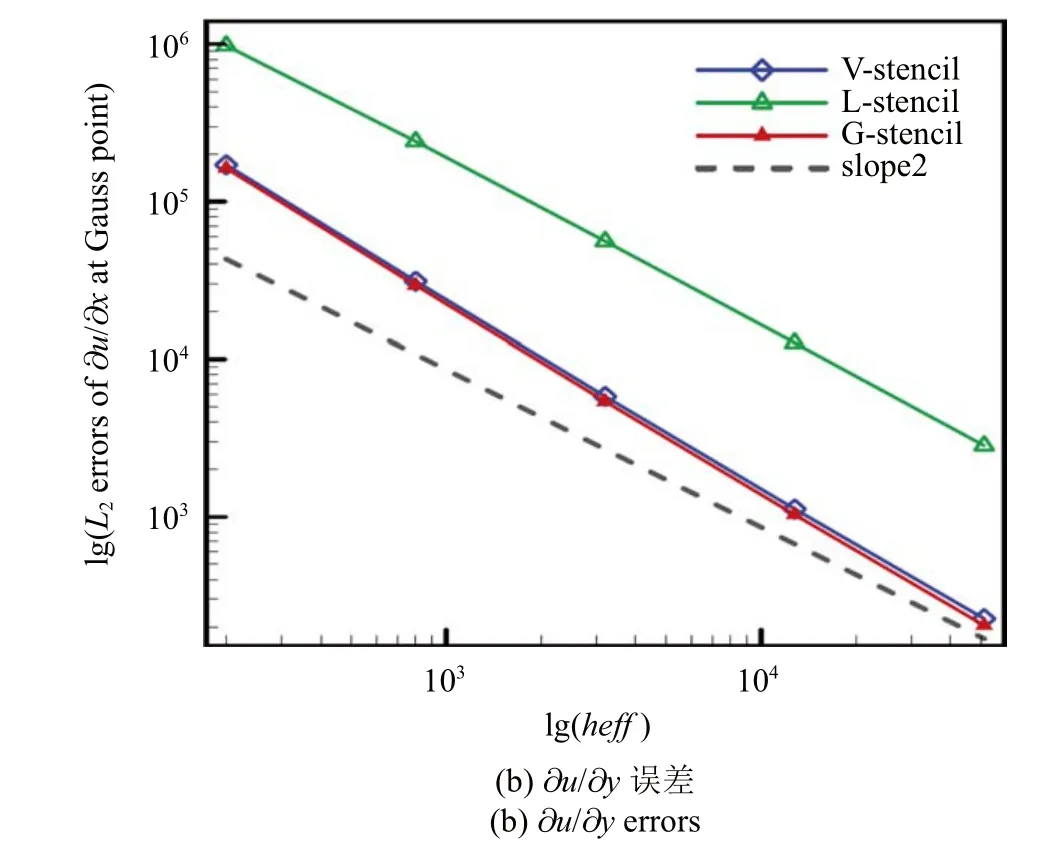
图18 高斯积分点处梯度L2 误差(续)Fig.18 L2 norm of gradient errors at Gauss point(continued)
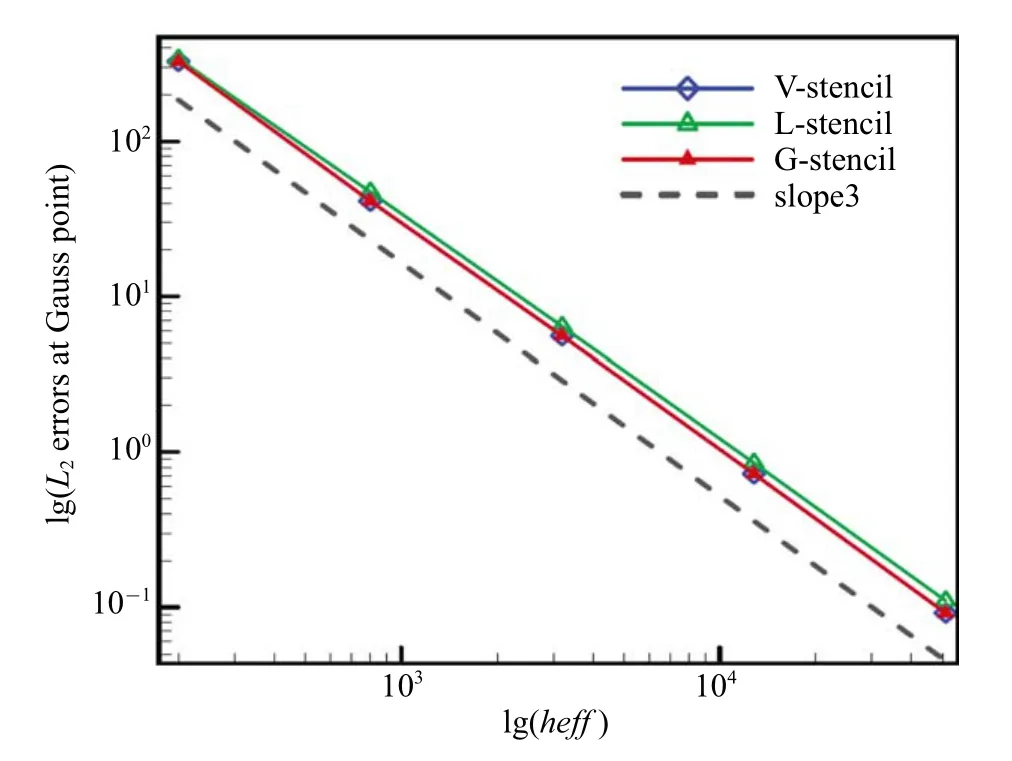
图19 高斯积分点变量点值L2 误差Fig.19 L2 norm of variable errors at Gauss point

表5 密网格上高斯点处的变量点值与导数的L2 误差Table 5 L2 errors of variable and derivatives at Gauss points
反观局部方向模板,由2.2 节的分析可知,在高度各向异性的三角形网格上,由于局部方向与壁面法向间存在较大偏差,导致模板单元无法较好地反映流动的各向异性特征.从重构结果与高斯积分点处的误差统计也可以看出,局部方向模板的计算误差较高.因此,当采用高度各向异性的三角形网格时,不宜使用这种模板选择方式.
4 结论
本文通过对比不同模板得到的变量梯度与高阶导数重构结果,验证了全局方向模板在高阶精度非结构有限体积方法中应用的可行性.首先从操作层面而言,相比局部方向模板,全局方向模选择方法的过程简便,避免了阵面推进与局部方向传递过程,显著降低了模板选择这个前处理过程的复杂程度; 相比常用的共点模板选择方法,新方法只需要在确定共点单元的基础上,找到其中与两个全局方向相交的网格单元即可,这个过程并未弓入任何复杂性.
其次从计算结果来看,不论网格拓扑是规则剖分还是随机剖分,采用全局方向模板得到的梯度与高阶导数误差明显低于局部方向模板,同时在计算高阶导数时,全局方向模板得到的(∂2u)/(∂x2) 与(∂2u)/(∂x∂y)误差值相比常用的共点模板更低.并且相比共点模板,全局方向模板的使用可有效减少重构过程所需的模板单元数量,在一定程度上可节约CPU 时间,提高计算效率.
此外,为检验不同模板的重构结果对实际计算的影响,本文还统计了高斯积分点处变量点值与一阶导数的误差.经检验,全局方向模板得到的变量点值及导数误差与共点模板接近,并稍低于共点模板,而局部方向模板的误差值相对偏高,不利于对流通量与黏性通量的构造.
综上,全局方向模板在梯度与高阶导数重构过程数值表现良好,并且重构优势在高斯积分点处得到了较好地验证,具有在高阶精度非结构有限体积求解器上应用并推广的可行性.接下来的工作将从两个方面开展,首先从应用层面,将进一步测试其在高精度非结构有限体积方法中的数值表现.其次从数值分析层面,在不同类型的网格上对重构矩阵的条件数与奇异性分析,以及相应的模板优化工作同样也是下一步研究的重点.

