认知无线电网络中基于预测的频谱感知方案

姚 阚，金子龙,2+，马廷淮

(1.南京信息工程大学 计算机与软件学院，江苏 南京 210044；2.南京信息工程大学 江苏省大气环境与装备技术协同创新中心，江苏 南京 210044)

0 引 言

与传统无线传感器网络不同，认知无线电网络允许节点机会性地使用授权频段进行通信[1]，实现这一功能的核心技术是频谱感知[2,3]。然而，由于多径衰减等负面影响，频谱感知精度不可靠。为了解决这个问题，协作频谱感知技术被提出并成为研究热点。但是，在以电池供能的无线设备中，频繁的频谱感知会减少网络的生命时间。文献[4-7]提出选取少量次级用户参与频谱感知，从而降低在频谱感知阶段的能耗。利用机器学习方法，文献[8-12]对以上方案进一步地强化，即节点对授权信道状态进行预测，决定是否进行频谱感知。但是以上的方案未考虑授权频谱可用性的时空差异性特点[13]，由于地理位置的不同，不同节点频谱可用性是矛盾的，进而导致预测的结果矛盾。因此在这种网络环境下，需要将处于不同网络环境的节点相互分离，降低对频谱感知决策的干扰。针对此问题，提出一种基于隐马尔科夫模型(hidden Markov model，HMM)预测算法的协作频谱感知方法，提高频谱感知精度和能效。

1 网络模型

假设有K个以电池供能的次级用户SU(secondary user)和一个融合中心FC(fusion center)组成进行协作频谱感知的认知无线电网络。同时网络中存在一个主要用户PU(primary user)，主要用户可任意占用授权信道。融合中心是一个信息共享、数据存储以及决策的中心，且不受能量的限制。网络以时分多址方式运行。在每个时隙开始时，次级用户会采用能量检测法对授权信道进行频谱感知，并将感知决策结果(“0”或“1”)发送至融合中心。融合中心利用次级用户的频谱感知数据建立HMM模型，并利用预测结果剔除不可靠节点(将在第2节中描述)。在剔除不可靠节点后，在剩余次级用户中根据剩余能量和全局感知精度选取少量次级用户(将在第3节中描述)参与频谱感知，并在决策后共享至其它节点。

次级用户的频谱感知可以表示为二元假设检验。H0和H1分别表示授权信道被主要用户不占用和占用。一个次级用户在对某一授权信道频谱感知时接收的信号可表示为[14]

(1)

其中，y(n)是次级用户处的接收信号，g(n)是加性高斯白噪声，α是信息增益，s(n)是主要用户发送的信号。

基于此，信道状态可通过下式进行决策

(2)

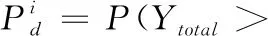
(3)

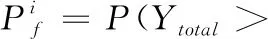
(4)

其中，γ表示主要用户信号在次级用户处的信噪比。

对于在融合中心处进行的协作频谱感知，其所有参与感知决策的全局检测概率Pgd和虚警概率Pgf采用OR融合规则获得

(5)

(6)

2 基于隐马尔科夫模型的信道状态预测

2.1 干扰域及隐马尔科夫模型参数定义

如图1所示，网络中存在3个次级用户(SU1,SU2和SU3)，一个融合中心FC，一个主要用户PU1。每个次级用户有一个受影响范围，表示主要用户出现在这个范围内，相应的次级用户将无法占用授权信道。基于此，网络可划分为8个不同的区域，被定义为干扰域(以下亦用IZ(interfered zone)表示)并用IZi表示第i个干扰域。如，当主要用户出现在干扰域3时，SU1和SU2将无法占用授权信道。基于此，隐马尔科夫模型的观测值为网络中的次级用户频谱感知结果的融合值，其在融合中心中的融合方式为

(7)

其中，Xt表示t时刻的融合观测值，n为次级用户的数量，Obi={0,1}表示第i个次级用户的观测值。

图1 干扰域网络

隐马尔科夫模型的状态转移概率、发射概率和初始状态概率分别定义如下：

状态转移概率矩阵用[A=a0,1a0,2…a0,M-1…aM-1,M-1]表示，其中ai,j表示主要用户从IZi转移到IZj的概率且

(8)

对于发射概率，用bIZi(Xt)表示t时刻真实状态为IZi且观测值为Xt的概率。在图1中，当主要用户出现在干扰域1时，SU1,SU2和SU3发送至融合中心的1-bit信息分别为“1”，“0”，“0”，融合后的观测值为“1”，真实状态为IZj，则

bIZ1(Xt=1)=P1(ot=1|qt=1)·
P2(ot=0|qt=0)·P3(ot=0|qt=0)

(9)

其中，Pi(ot|qt)表示SUi在真实状态为qt时观测值为ot的概率，且

(10)

(11)

因此由式(10)，式(11)可得

(12)

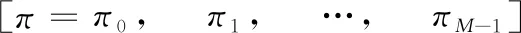
(13)

2.2 信道状态预测算法

信道状态预测过程由两个阶段构成：训练和预测。

2.2.1 Baum-Welch训练算法

在训练阶段，根据历史频谱感知数据，融合中心使用Baum-Welch算法得到隐马尔科夫模型的3个参数λ(初始状态概率π、状态转移概率A和发射概率B)。Baum-Welch算法是期望最大化算法(expectation-maximization algorithm，EM)的一种特殊情形。其过程简述为：

(1)初始化HMM模型的参数λ0;

(2)利用观测值序列X推导第k-1次的HMM参数λk-1，并将λk-1作为第k次迭代的初始参数;

(3)当P(O|λk)≤P(O|λk-1)时，迭代停止，此时获得的参数λk即为最优参数。

其伪代码见表1。

表1 Baum-Welch 算法

2.2.2 基于前向算法的预测

(1)初始化

αi(0)=a1,i·b1,i(X0)

(14)

(2)递归

αi(T-1)=P(X0,X1,…,XT-1,qT-1=IZi|λ)

(15)

(16)

(3)信道预测：在获取T-1时刻全部的前向概率后，T时刻的前向概率为

αi(T)=P(X0,X1,…,XT,qT=IZi|λ)

(17)

对XT取全集Ω={X0,X1,…,Xn-1}可得

IIZi(T)=P(X1,X2,…,Ω,qT=IZi|λ)

(18)

(19)

基于等式(19)，T时刻最有可能的信道状态为

(20)

在得到IIZi(T)后，对其值进行二进制解码，可知下一时隙会受主要用户活动干扰的次级用户，并将其加入受干扰集SIP,剩余次级用户即为不受干扰集SNIP。

3 协作频谱感知

在完成对次级用户的分组后(即SNIP和SIP)，在下一时隙开始时，为了降低频谱感知中的能耗，SIP中的次级用户将停止频谱感知，而SNIP中的次级用户将正常进行协作频谱感知。同时将选取少量可靠节点参与频谱感知进一步强化能效。

可靠节点的选择考虑其剩余能量和全局检测概率两个参数。

3.1 剩余能量定义和计算

(21)

其中，Ebit为次级用户发送1-bit信息的能耗，e为放大器功耗，di为第i个次级用户到融合中心的距离。

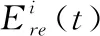
(22)

3.2 感知次级用户选择

参与协作频谱感知的次级用户应满足全局检测概率的前提下，剩余能量高。全局检测概率Pgd由式(5)可得，则感知次级用户的选择步骤为：

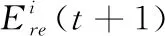
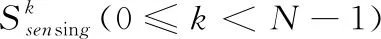
(23)

(3)若k=1时无满足条件的节点组合，则计算k+1时感知节点的组合即

根据等式(5)计算每个组合的全局检测概率，重复步骤(2)的节点组选择过程；

(4)若没用满足的节点组合，重复步骤(3)的过程，直至找到一个满足条件的感知节点组，此时参与协作频谱感知的次级用户数量为k。

3.3 信道状态最终决策

选出的k个次级用户在下一时隙进行频谱感知，并将结果发送给融合中心，融合中心使用Majority-rule进行信道状态决策，即

(24)

其中，I{Oi=1}为指示器，表示当SUi的频谱感知结果为“1”时其取值为1，否则为0。

融合中心在做出决策后，会将决策结果共享至SNIP的其它次级用户。

4 仿真分析

为了验证所提方案的有效性，本节中与两个方案进行对比实验。第一个方案为单节点频谱感知，即不进行协作频谱感知，全部节点进行独立的预测和频谱感知。第二个方案为文献[12]提出的，不剔除不可靠次级用户下进行的协作频谱感知，以下用RN(redundant nodes)代称该方案。

在MATLAB仿真平台下，网络环境中包括1个主要用户以及10个次级用户，且假设每个次级用户的干扰域与至少1个其它次级用户的干扰域重叠。同时为了探究所提方案对主要用户活动不同剧烈程度的适应能力，定义RT为主要用户占用信道的概率，即RT越大，次级用户受影响剧烈。考虑到RT取值较低时主要用户对次级用户的影响过低，取值过高时次级用户几乎无法占用授权信道，故RT取值范围为0.2到0.8。

方案性能从能耗以及频谱利用率两个方面进行对比。仿真运行12 500次，其结果如图2到图4所示。

图2给出了单节点频谱感知方案、RN方案以及文中提出的提出不可靠节点后的协作频谱感知方案在RT=0.5时的网络能耗曲线。从图2可以看出，单节点方案的能耗高于其它两种选择少量节点进行频谱感知的方案。而剩余两种中，提出的方案在能耗上低于RN方案，因此在降低能耗上，本文提出的方案更优。

图2 RT=0.5时网络能耗对比

图3给出了RT=0.5时RN方案和提出的方案在频谱利用率上的对比，在仿真中，频谱利用率被定义为授权信道为空闲且被次级用户占用的比例。从图3可以看出，总体上，本文提出的方案的频谱利用率高于RN方案。

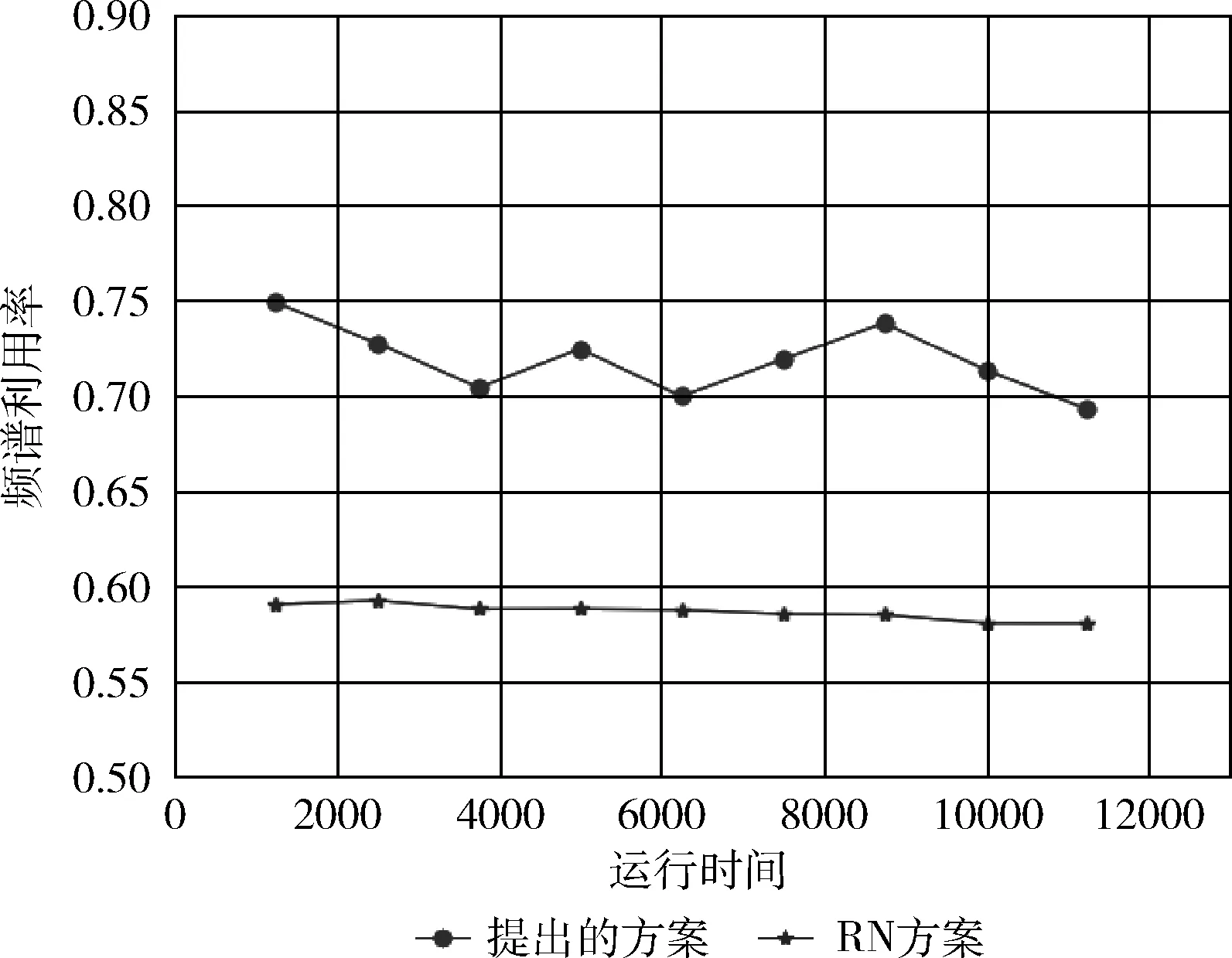
图3 RT=0.5时网络频谱利用率对比

图4给出了RT增大下的能耗折线图，可以看出两种方案的能耗均随着RT增大而降低。当RT较小时基于不可靠节点剔除的协作频谱感知方案的能耗较低，随着主要用户对授权信道的占用频率增大，RN方案的能耗低于本文提出的方案。

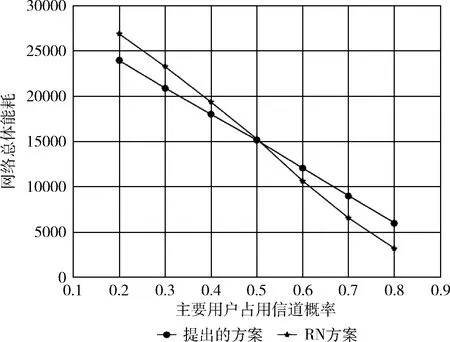
图4 不同RT时的网络能耗对比

但结合图5，随着RT的增大，RN方案的频谱利用率不断降低，而本文提出的方案的性能仍高于RN方案。

图5 不同RT时的网络频谱利用率对比

为了进一步验证这一点，定义吞吐量-能耗比

(25)

吞吐量-能耗比越高则能量利用率越高，由图6可看出，随着主要用户占用授权信道频率的增加，两种方案在吞吐量-能耗比上总体上较稳定，且本文提出的方案的性能优于RN方案。

图6 不同RT时的网络吞吐量-能耗对比

5 结束语

本文在隐马尔科夫模型的基础上，提出了基于信道状态预测的协作频谱感知算法。算法共分为两个部分，首先是利用预测结果剔除不可靠次级用户，其次在剔除不可靠次级用户后，综合全局检测概率和剩余能量，选择少量的次级用户进行频谱感知。不可靠次级用户剔除中，利用历史频谱感知数据建立隐马尔科夫模型，有效地对次级用户进行分类，避免不可靠节点对信道状态决策的干扰。在下一阶段的协作频谱感知中，综合剩余能量以及全局检测概率选择少量次级用户进行频谱感知，有效地提高了能效。仿真结果表明，在满足频谱感知精度的前提下，文中提出的方案能够降低网络能耗，优化频谱利用率。