基于有限时间命令滤波机械臂的阻抗控制

林高荣，刘加朋，于金鹏

（青岛大学 自动化学院，青岛266071）

随着机械臂在社会生活中的运用日益广泛，其工作环境也越来越复杂，仅依靠机械臂的位置控制已不能满足当今的工作需求。 人与机械臂的交互协作技术在社会生产中的运用已成为未来发展的趋势，同时为提高人/机械臂交互系统的安全性与柔顺性，对更高精度的机械臂力/位控制策略有更迫切的需求，因此对机械臂更好地进行力/位控制已成为一个重要的研究热点。

为解决这一难题，海内外专家学者进行了大量研究，提出了力/位混合控制[1]、阻抗控制[2]等力/位控制方法。 阻抗控制具有抗扰动能力强、计算量相对较少，以及易于机械臂进行力控制等特点[3]，因此受到海内外研究人员的广泛关注。

1 机械臂阻抗控制技术的相关研究

近年来，机械臂的阻抗控制技术得到了极大的发展。 文献[3]针对机械臂系统，研究了阻抗控制器的设计方法，但是未能实现对力的精准控制。 文献[4]通过力传感器测量反馈力信号来估计位置环境模型，利用力信号分析，并结合阻抗控制，从而使机械臂末端在未知接触环境表面上的力控制精度得到了提高；文献[5]研究了模糊自适应的阻抗控制方法，该方法通过模糊自适应技术，不断调整期待阻抗参数，并以滑模位置控制作为内环控制器，提高了控制系统的鲁棒性；文献[6]利用模糊自适应方法逼近未知的机械臂系统模型参数，并设计阻抗控制器，该控制器取得较好的力/位控制效果。然而，文献[6]所提机械臂反步法阻抗控制方法在跟踪期望信号上响应速度较慢，造成机械臂系统的跟踪性能相对较差。 有限时间控制[7]能够使被控系统在有限时间内系统输出信号趋于期望信号，机械臂系统的有限时间控制能够使机械臂系统在有限时间内具有较快的响应速度，同时获得更高的控制精度。

同时，文献[6]采用反步法进行控制器设计，但在使用反步法设计控制器的过程中，虚拟控制律的反复求导提高了“计算复杂性”。 为解决这个问题，在此引入了命令滤波误差补偿技术[8]，该技术通过补偿信号解决滤波误差问题，并降低控制器设计的复杂性。

基于以上讨论，文中提出多关节机械臂的有限时间命令滤波阻抗控制FTCFC（finite-time command filtered control），通过仿真结果验证了所设计的机械臂系统控制器的有效性及可行性。 所提控制方法的优点如下：

1）首次将有限时间命令滤波反步控制与阻抗控制方法相结合，实现了机械臂在有限时间内较好地进行力/位控制；

2）采用命令滤波技术，解决了文献[6]中经典反步法设计控制器过程中虚拟控制律反复求导的问题，简化了控制器的设计，有利于实际工程运用；

3）与文献[6]控制方法相比，在此所提控制方法提高了机械臂力/位跟踪的响应速度，并减小了跟踪误差。

2 机械臂数学模型及初步变换

机械臂的运动学方程[9]如下：

由方程（1）转换，可得

其中

式中：x 为机械臂末端在笛卡尔坐标系下的位置；o为机械臂运动空间的维度，o≤3；q 为机械臂各关节的角度；J（q）为从机械臂各关节到末端转换的雅可比矩阵；n 为机械臂的自由度。

机械臂动力学方程[10]如下：

其中

机械臂末端位置与末端力的阻抗控制关系[11]为

其中

式中：Fe为机械臂末端力；Fd为机械臂末端期望力；Md为机械臂期望惯性矩阵；Bd为机械臂期望阻尼矩阵；Kd为机械臂期望刚性矩阵。 在机械臂未与外部物体接触时，Fd=0；当x=xd，有Fe=0。

将式（2）代入式（3），可得

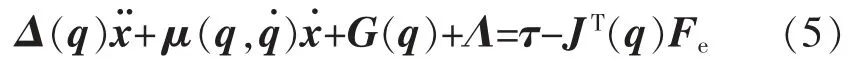
其中

由式（5）变换，有

为了便于有限时间命令滤波阻抗控制器的设计，令

引理1对于任意实数λ1>0，λ2>0，0<γ<1，则有限时间稳定的扩展Lyapunov 条件为

其中，系统的收敛时间Tr可估计[12]为

引理2有限时间命令滤波器形式[13]为

其中

式中：αr为滤波器的输入信号；φ1，φ2为滤波器的输出信号；R1，R2为滤波器参数。 选取合适的R1和R2，经过有限时间的瞬态过程后，未受到输入噪声的情况下，可得

以及该动态系统相应的解为有限时间稳定。 当给出滤波器的输入受噪声影响时，输入噪声满足不等式

然后，在有限时间内构造完全依赖于滤波器参数R1和R2的不等式，即

式中：ϑ1和ζ1均为正常数，且取决于滤波器中的设计参数；和均为正常数[14]。

3 有限时间命令滤波控制器

根据反步法原理，定义误差变量为

式中：xd为给定的期望信号；虚拟控制律α 为滤波器输入信号；x1，c为滤波器的输出信号。 定义滤波误差补偿信号为ξi=zi-vi，其中i=1，2。虚拟控制律和滤波补偿信号的具体结构设计如下：

步骤1选取Lyapunov 函数为

对其求导后，可得

设计虚拟控制律α 和补偿信号ξi，即

其中，控制增益k1>0，s1>0； 参数β，h1均为常数，0<β<1，h1>0。 将式（10）（11）代入式（9），可得

步骤2选取Lyapunov 函数为

对其求导后，可得

其中

定义非线性函数

根据万能逼近定理[15]，对于任意小的常数εi>0，存在模糊逻辑函数WiTS（Z），使得

其中

式中：δi为逼近误差。 又因为，则由杨氏不等式，可得

式中：l 为常数，且l>0。

设计真实控制律τ，补偿信号ξ2和自适应律导数，即

其中，控制增益k2>0，s2>0；参数η，m，h2均为常数，η>0，m>0，h2>0。

定义

由式（19），可将不等式（15）转换为

4 稳定性证明

为了验证所提控制方法的稳定性，可由杨氏不等式得

将其代入式（21），可得

同理，可得

综合式（25）（26），可得

由vj= [vj，1，vj，2，…，vj，n]T和文献[16]，可推导出：

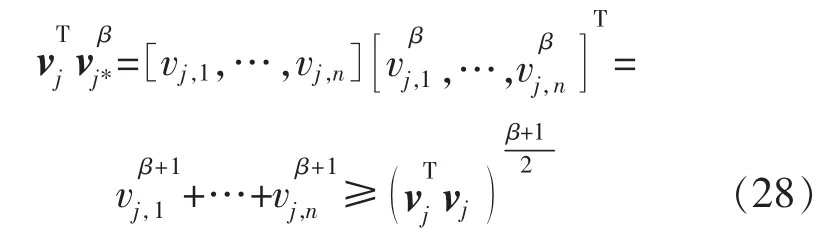
将式（24）（27）（28）代入式（23），可得

其中

将式（29）改写为

由式（30）可知，选取合适的参数，可使

由引理1 可知，vj（j=1，2，…，n）将在有限时间T1内收敛于域之内。 由于zj=vj+ξj，如果能证明ξj在有限时间内收敛于一个极小的零邻域内，就能够使跟踪误差zj在有限时间内收敛于一个极小的零邻域内。

在此选取Lyapunov 函数

证明命令滤波误差补偿ξ1和ξ2在有限时间内收敛于一个极小的零邻域内。 式（31）对时间求导，可得

式（32）利用文献[16]，可推导出：

令

且

可得

根据引理2 可知，在有限时间T2内有

且将式（33）（34）代入式（32），那么t>T2，有

将式（35）改写为

由式（36）可知，选取合适的参数，可使

由引理1 可知，ξr（r=1，2）将在有限时间T2内收敛于域内。

5 仿真试验

在垂直平面上的二自由度机械臂上对所提控制方法进行仿真试验，由此证实所提控制方法的有效性。 将所提出的有限时间命令滤波阻抗控制方法与文献[6]控制方法，进行仿真比较，由式（6）可知仿真试验的旋转关节二自由度机械臂系统模型为

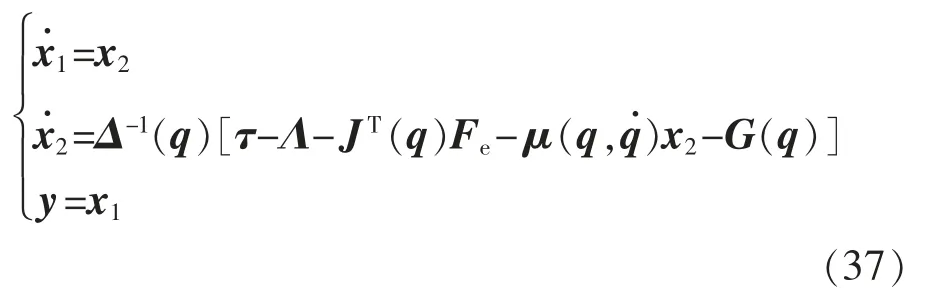
其中

式中：x1，1，x1，2分别为二自由度机械臂在笛卡尔坐标系上机械臂末端在X，Y 轴上的位置；q 为机械臂各关节角度。 二关节机械臂模型如图1所示。

图1 二关节机械臂模型Fig.1 Two-link manipulator model

二自由度机械臂的惯性矩阵D（q），科里奥利力与离心力矩阵C（q，），重力项矩阵G（q）及雅可比矩阵J（q）的定义如下：

式中：mi，li分别为机械臂的第i 节连杆的质量、长度，i=1，2；lcorei为机械臂的第i-1 关节到第i 节连杆质心的距离；Ii为垂直于X-Y 坐标系连杆i 质心的转动惯量。

表1 二关节机械臂参数Tab.1 Two-link manipulator parameters

二自由度机械臂末端的期待跟踪轨迹为

其中t∈［0，20］。 选取二自由度机械臂其它未建模动态为

对于二自由度机械臂模糊自适应阻抗控制法，其控制参数选取为k1=8，k2=6，l=0.5，η=1，m=0.25；

对于二自由度机械臂模糊自适应有限时间命令滤波阻抗控制法，其控制参数选取为k1=6，k2=8，s1=2，s2=2，β=0.6，l=0.5，η=1，m=0.25，h1=1，h2=1，R1=20，R2=0.6。

该二自由度机械臂期待阻抗参数选为Md=I，Bd=diag［15，15］，Kd=diag［60，60］。 模糊逻辑系统选择模糊集为

在此所提出的控制方法为模糊自适应FTCFC，对比控制方法为模糊自适应阻抗控制法。 本文控制方法与对比控制方法机械臂末端X 轴、Y 轴上位置跟踪曲线及跟踪误差比较分别如图2，图3所示。

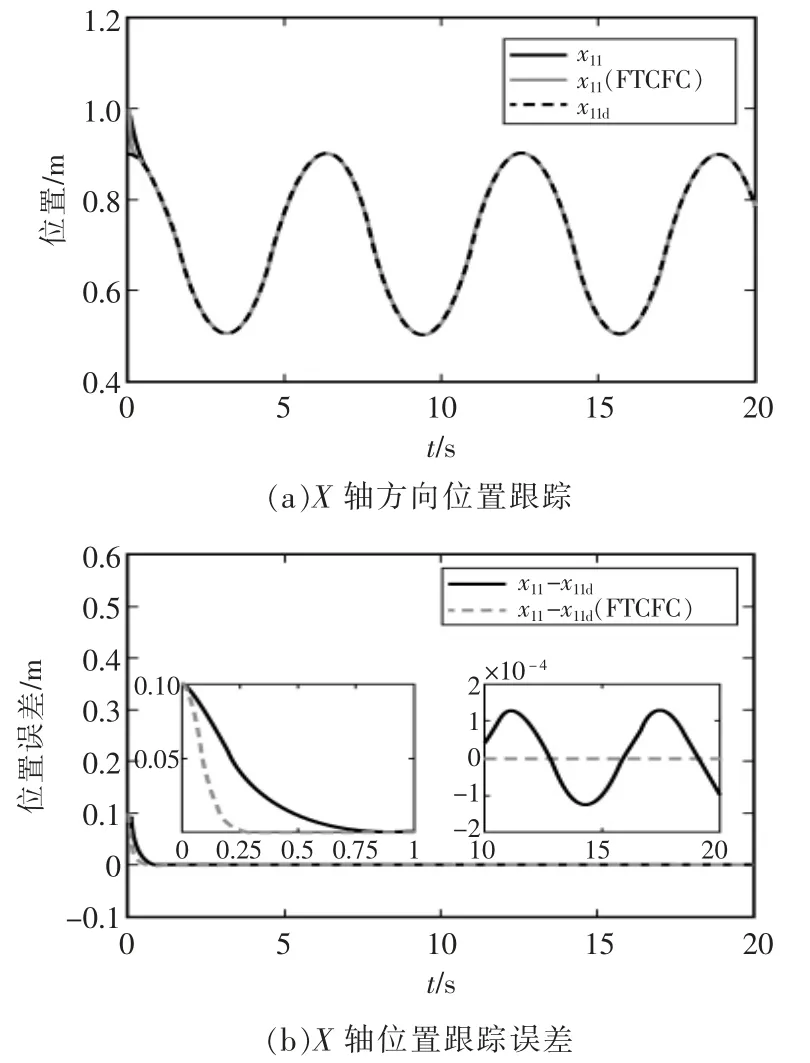
图2 X 轴方向位置跟踪与位置跟踪误差Fig.2 X-axis position tracking and position tracking error

图3 Y 轴方向位置跟踪与位置跟踪误差Fig.3 Y-axis position tracking and position tracking error

由图可见，本文控制方法能够很好地跟上期望曲线，并且与对比控制方法相比较，有着更快的响应速度、更小的跟踪误差。

本文控制方法与对比控制方法机械臂末端X轴、Y 轴上力跟踪曲线及力跟踪误差比较分别如图4，图5所示。

图4 X 轴方向力跟踪及其误差Fig.4 X-axis directional force tracking and its error

图5 Y 轴方向力跟踪及其误差Fig.5 Y-axis directional force tracking and its error

由图可见，本文控制方法能够使机械臂末端接触力很好地跟上期望接触力，其与对比控制方法相比较能更快跟上期望接触力，并且有着更小的接触力跟踪误差。 真实控制律τ 如图6所示，由图可见其均在合适的范围内。

图6 控制律的对比Fig.6 Comparison of control laws

6 结语

针对人与机械臂交互系统的安全性与柔顺性的需求，在此以模糊自适应反步法为基础，构造了机械臂的模糊自适应有限时间命令滤波阻抗控制器，实现了机械臂末端力/位在有限时间内较为快速精确地跟上期望信号。 所提出的控制方法与现有的控制方法相比，提高了机械臂系统力/位跟踪的响应速度以及减小了跟踪误差。 仿真对比试验验证了所提出控制方法的可行性。