基于优化极限学习机的基坑侧位移变形预测

王 承 敏

(上海城地岩土设计有限公司,上海 200333)

0 引言

随着城市化建设的快速发展，基坑工程日益增加；同时，受基坑开挖空间临空面影响，其施工过程会出现侧向位移变形，直接关系施工安全，使得基坑侧位移研究显得格外重要[1,2]。目前，在基坑侧位移研究方面，已有相关学者开展了相应研究，如马将[3]基于基坑变形成果，开展了基坑空间变形效应分析，其中涉及基坑侧位移变形特征分析及预测研究，为评价基坑稳定提供了理论依据；耿大新等[4]利用静力平衡微分方程构建了基坑侧位移计算模型，其结果与实测结果相符，为基坑侧位移计算提供了一种新的方法。上述研究虽取得了一定成果，但未针对基坑侧位移开展专门的预测研究，或未涉及极限学习机在基坑侧位移中的应用研究，进而仍有必要拓展基坑侧位移的变形预测思路。同时，在基坑变形预测方面，也有学者开展了相应研究，如陈家骐等[5]利用优化灰色模型构建了基坑变形预测模型，而宋楚平[6]、贾哲等[7]均利用神经网络构建了基坑变形预测模型，所得预测结果也与实测结果较为接近，但上述研究均为涉及基坑侧位移变形预测研究，也未进行极限学习机的应用探讨。因此，该文以极限学习机为理论基础，通过多种优化算法保证其参数最优性，进而构建出基坑侧位移的优化极限学习机预测模型，以期为工程施工提供一定理论指导。

1 基本原理

该文旨在以极限学习机(Extreme Learning Machine,ELM)为基础，通过模型参数的不断递进优化构建出基坑侧位移变形预测模型，进而为基坑支护结构稳定性评价提供一定的指导[8]。ELM模型是一种新型前馈神经网络，具有三层网络结构，若基坑侧位移监测成果为(xi,ti,i=1,2,…,N)，则其训练过程中的预测值yj可表示为：

(1)

其中，L为隐层节点数；βi,wi均为连接权值；g(x)为激励函数；bi为阈值；N为样本数。

由于ELM模型可实现训练过程的零误差逼近，一般具有较高的预测精度，但其激励函数和隐层节点数由使用者确定，依赖性、主观性较强，加之初始输入权值和阈值对预测过程的稳定性具有一定影响，使得ELM模型的泛化能力减弱。因此，为切实保证基坑侧位移变形预测模型的预测精度，有必要对其相应参数进行优化处理。

1)激励函数优化。

ELM模型的常用激励函数包括Sigmiod型、Sine型和Hardlim型，三者的适用性不同，为确定最优激励函数，该文提出通过三种激励函数的预测效果对比来确定最优激励函数，即对三类激励函数的预测效果均进行试算，将预测效果最优者作为该文ELM模型的最优激励函数。

2)隐层节点数优化。

在传统神经网络模型中，多是利用经验公式确定隐层节点数，即：

(2)

其中，m，n分别为输入、输出层节点数。

为保证隐层节点数的最优性，该文以式(2)经验值为中心，对其取值范围适当扩展，再进行取值范围内所有隐层节点数的预测效果对比，选取预测效果最优者即为该文ELM模型的隐层节点数。

为便于后文过程描述，将上述两参数优化后的预测结果定名为初优ELM预测结果。

3)初始权值和阈值优化。

如前所述，模型的初始权值和阈值会影响预测过程的稳定性，也有必要对其进行优化处理，且鉴于遗传算法(Genetic Algorithm，GA)在参数优化中的普遍适用性，进而利用其优化ELM模型的初始权值和阈值，具体优化过程如下：

a.对遗传种群的初始参数进行设置，如将其规模设置为300，最大迭代次数设置为250次，交叉概率设置为0.25，变异概率设置为0.35，其余参数随机设定。

b.以预测误差构建优化效果评价的适宜度函数，并计算得到初始适应度值。

c.通过交叉、变异等操作，不断迭代繁衍新种群，并计算适宜度值，并将其值与初始适应度值对比，确定出最佳的适应度值。

d.当达到优化期望或最大迭代次数时，输出最优初始权值和阈值，以达到初始权值和阈值的优化处理。

类比，为便于后续分析，将遗传算法优化后的预测结果定名为GA-ELM预测结果。

4)泛化能力及动态预测优化。

由于ELM模型是基于风险最小化原则构建的预测模型，使其泛化能力相对偏弱，因此，再利用贝叶斯估计提升其泛化能力，将优化后的预测结果定名为B-GA-ELM预测结果；同时，结合工程实例，基坑侧位移数据具持续增加特征，进而有必要在前述基础上构建动态预测模型，以实现基坑侧位移的动态预测，并将其预测结果定名为DB-GA-ELM预测结果。鉴于贝叶斯估计对ELM模型的优化处理及动态预测过程已在文献[9]中进行了详述，限于篇幅，该文不再赘述。

为准确评价前述不同预测过程的预测效果，该文将预测结果的相对误差均值及其标准差作为预测效果的评价指标，前者用于评价预测精度，而后者用于评价预测结果的稳定性，两者均是越小越好。

2 实例分析

2.1 工程概况

春申湖路站隶属苏州地铁四号线，位于春申湖南侧，基坑外包长199.6 m，宽度为19.7 m，端头开挖深度18.5 m，标准段开挖深度为16 m；站址区属冲积湖平原地貌，地势较为平坦，地面标高介于2.72 m～4.02 m，地形起伏较小，且结合钻探成果，基坑开挖范围共涉及四类土层，其中两类土层又可细分为两个亚层，各类土层的基本特征参数如表1所示。

表1 土层特征参数统计

春申湖路站基坑周边地表水及地下水均较为丰富，两者特征如下：

1)地表水。站址区周边地表水系发育，具水网化分布特征，其中，最大地表水系为文灵河，水深1.3 m～2.3 m；同时，地表水多接受降雨补给，并以蒸发或向地下水补给排泄为主。

2)地下水。按赋存条件，区内地下水主要可分为潜水、微承压水和承压水，其中，潜水主要赋存于填土层孔隙中，历史最高潜水位为2.63 m，最低潜水位为0.21 m，受降雨或地表水补给为主；微承压水主要赋存于④1粉粘夹粉土层中，水头标高约1 m，对基坑施工影响较大，需进行降水处理；承压水位于基坑坑底以下，埋深大于32.5 m，对基坑施工影响有限，主要接受地下水径流补给或越流补给。

为准确掌握基坑施工过程的变形特征，对其支护结构进行了侧位移监测，共计布设了26个监测点，监测频率按2 d/次，共计得到26期监测成果；通过统计，得26个基坑侧位移监测点的变形值如图1所示。由图1可知，CX-08监测点的侧位移值相对最大，达22.4 mm，而CX-02监测点的侧位移值相对最小，值12.64 mm，各监测点的侧位移均值为18.43 mm。

为验证该文预测思路，该文以两个侧位移最大监测点的变形成果作为该文模型效果验证的数据来源，即以CX-08监测点和CX-22监测点进行该文预测思路的有效性研究，其侧位移变形曲线如图2所示。

2.2 预测分析

限于篇幅，该文以CX-08监测点为例，详述对比不同优化阶段的预测效果，再利用CX-22监测点进行有效性验证；同时，在预测过程中，以1～21周期为训练样本，22～26周期为验证样本。

1)不同优化阶段的预测效果分析。

如前所述，以CX-08监测点为例，详述对比不同优化阶段的预测效果。

首先，对三类激励函数的预测效果进行统计，得表2。据表2，得三类激励函数的预测效果存在明显差异，说明三者在基坑侧位移中的预测效果不同，进行优化筛选的必要性显著；对比三者的预测效果，得出Sigmiod型不仅具有相对最佳的预测精度，还具有相对最好的稳定性，而Sine型的预测效果相对最差，Hardlim型间于两者之间。因此，确定该文ELM模型的激励函数为Sigmiod型。

表2 不同激励函数的优化筛选

其次，通过经验公式计算得到隐层节点数的经验值为12，将其取值范围设定为9～15，并计算得到不同隐层节点数的预测结果如表3所示。据表3，随隐层节点数增加，相对误差的均值和标准差均表现为：先减小后增加，后期增加幅度要小于前期减小幅度，当隐层节点数为13时的预测效果相对最优，说明隐层节点数对预测效果具有一定影响，且在经验值附近，宜取大值，不宜取小值。因此，通过上述，确定该文ELM模型的隐层节点数为13个。

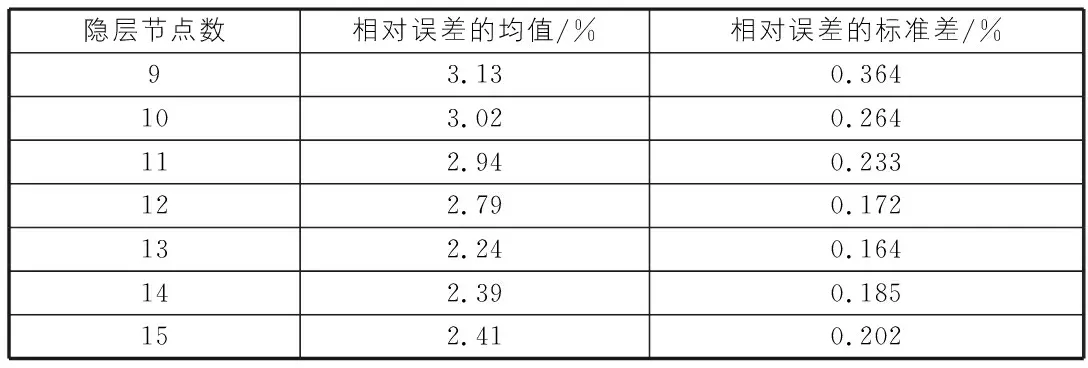
表3 不同隐层节点数的优化筛选

再利用遗传算法优化ELM模型的初始权值和阈值，并将其预测结果与前述初优ELM预测结果进行对比，得表4。据表4，在相应验证节点处，GA-ELM预测模型的相对误差值均小于初优ELM预测结果的相对误差值，加之前者较后者具有相对更小的相对误差均值和标准差，说明通过遗传算法优化能进一步提高预测精度及稳定性，验证了遗传算法优化的有效性。

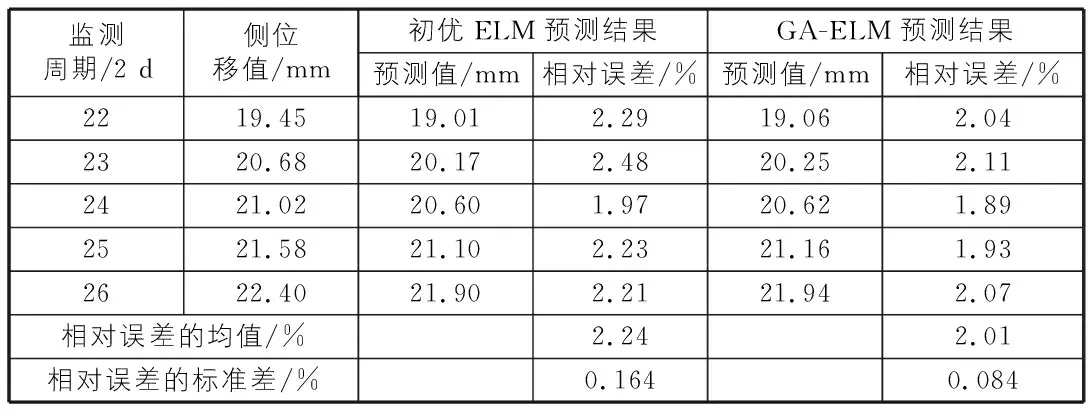
表4 连接权值和阈值的优化结果

最后，再利用贝叶斯估计和动态预测思路进行基坑侧位移优化预测，结果如表5所示。据表4，表5，通过贝叶斯估计和动态预测优化，得出预测结果的相对误差均值和标准差均呈进一步减小趋势，进而验证了两类优化方法的预测效果；同时，DB-GA-ELM预测模型的相对误差均值为1.77%，相对误差的标准值为0.096%，说明该文预测模型不仅具有较高的预测精度，还具有较强的稳定性，也验证了该文预测思路的准确性。

表5 贝叶斯估计和动态预测的优化预测结果

2)有效性验证预测分析。

为进一步验证该文预测模型的有效性，该文再利用CX-22监测点进行变形预测研究，通过预测统计，得其结果如表6所示。

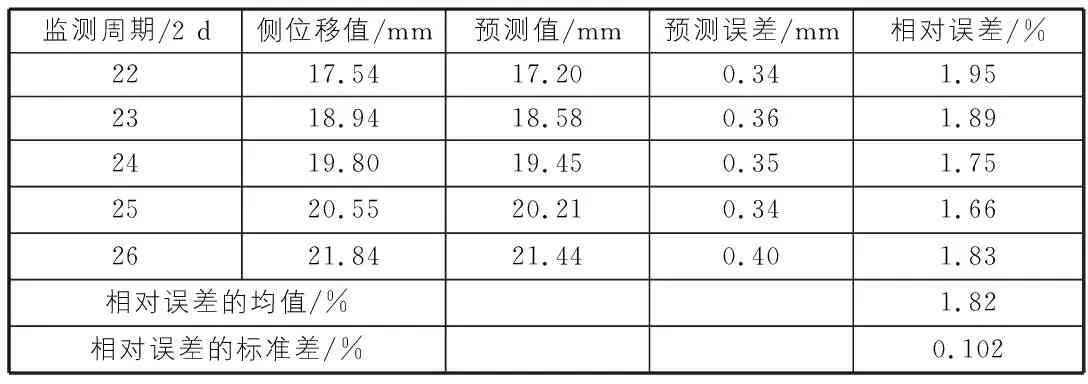
表6 CX-22监测点的预测结果

由表6可知，CX-22监测点的最大、最小相对误差分别为1.95%和1.66%，相对误差的均值为1.82%，而相对误差的标准差为0.102%，进一步说明该文预测模型具有较高预测精度和稳定性。

同时，为进一步佐证该文预测模型相对于传统预测模型的优越性，再对两监测点进行传统BP神经网络预测，其与该文预测结果的对比结果如图3所示。由图3可知，该文预测模型的预测精度要明显优于传统BP神经网络的预测精度，说明该文模型在基坑侧位移预测方面具有较强的优越性。

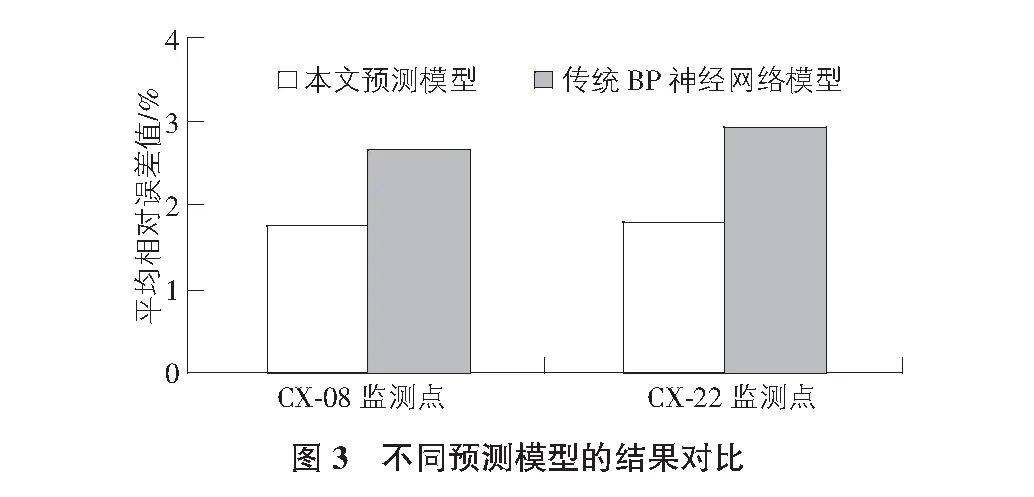
通过上述分析，充分验证了该文预测模型的预测精度及稳健性，适用于基坑侧位移变形预测，值得推广预测研究。

3 结论与讨论

通过优化ELM模型在基坑侧位移预测中的应用研究，主要得出如下结论与讨论：

1)ELM模型适用于基坑侧位移预测，且通过不断迭代递进优化，能有效提高预测精度，因此，建议在预测模型的构建过程中，应充分优化模型参数，确保参数最优性。

2)该文优化ELM模型不仅具有较高预测精度，还具有较强的稳定性，且相较于传统神经网络模型的优越性明显，值得推广应用研究。

3)限于篇幅，由于该文仅对基坑侧位移进行了预测分析，建议在条件允许前提下，可将该文预测模型推广于其他基坑监测项目的预测过程中，以验证其普遍适用性。