花坛的面积

刘艺轩

数学很奇妙，也很有挑战性。最近，我们正在学习正方形的面积，李老师带来了一道很有意思的题目：

一个正方形的花坛，如果把花坛的边长加长3米，花坛的面积就增加39平方米，那么原来正方形花坛的面积是多少？

正方形的面积计算公式是边长乘边长，需要知道边长才能求出它的面积。于是，我绞尽脑汁思考怎么先求出正方形的边长。我先尝试画了一个小正方形（空白部分），代表原来的正方形花坛，然后画了一个比它大一点的正方形，代表边长增加3米以后的正方形花坛，绿色部分就表示增加后的面积（如图1），也就是39平方米。

小正方形在大正方形的正中间，怎么求小正方形的边长呢？边长增加3米之后就有了大正方形的边长，可是，大正方形的边长又该怎么求呢？我左看看，右看看，怎么也想不到答案。之后，我随手列了一个算式，39÷3=13，但怎么也不明白其中的含义，我只好向妈妈求助。

起初，妈妈也没什么头绪。后来，妈妈想用方程来解决这个题目，可是我们还没有学到用方程解决问题，于是，她又放弃了。再读了读题目，妈妈好像有了一些想法，开始用铅笔画图，不过她跟我画的图有点儿不一样（如图2）。

“妈妈，您为什么要把这个小正方形放到大正方形的一角呢？”我疑惑地问道。

妈妈说：“我只是按照题目的要求，把边长延长了3米，就画出来了呀。”

“难道我的画法不正确吗？”我又问妈妈。

思考了一会儿之后，妈妈兴奋地说：“一样的呀。在图1中，如果我们将小正方形不断地向左下角拖拽，这个过程中，不管是大正方形还是小正方形，它们的面积都不发生变化，所以增加的面积也不会变，而且还可以很清晰地看到两个正方形的边长之间的对比，有利于我们解决问题。”

我似懂非懂地点了点头，并在图上画了两笔后，说：“图1中的绿色部分其实是由一个正方形和两个长方形组成的。”

妈妈提示我：“你觉得，我们是否可以把小正方形下方的这个长方形（黄色部分）剪下来拼到上面长方形的右侧？”

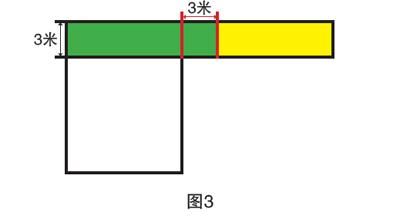
“可以呀。我明白了，现在这个阴影部分就变成了一个大的长方形。题目告诉我们这个大长方形的面积是39平方米，那么，它的长就是39÷3=13（米）。”我越讲越兴奋。

从图3中，我还发现13米是由小正方形的两条边加上3米组成的，这样我可以计算出小正方形的边长是（13-3）÷

2=5（米）了。知道了小正方形的边长，计算花壇的面积就很简单了：5×5=25（平方米）。

指导老师  李小强