局部遮挡条件下的普通工件定位检测

余振军，孙 林，贾坤昊，孙 洋

(山东科技大学 测绘科学与工程学院，山东 青岛 266590)

0 引 言

目标定位检测作为图像处理的关键技术，一直是模式识别的热点问题。目前，大致分为以下思路：一种是传统计算机视觉检测方法，一种是基于深度学习的目标定位检测方法。传统方法中，通常利用目标的轮廓信息构建形状描述子，通过形状描述子间的相似度实现目标的匹配与定位。形状上下文[1,2]是近年来目标定位识别的主流算法，能够对轮廓信息进行很好的描述，对非线性的形变具有很好的识别效果，但是，形状上下文算法是利用极坐标切线来保证旋转不变性的，容易受到噪声干扰；吴晓雨等[3]利用采样点个数最多的角度区域进行对比，找到目标的旋转角度，并采用减枝的方法加快匹配；冯祥卫等[4]利用高斯窗函数代替传统形状上下文中的Bins，增加算法的抗噪能力；张桂梅等[5]利用内距离代替欧氏距离对目标进行描述，对非刚性变化有较强的鲁棒性；另外，利用轮廓几何特征之间的相似度进行匹配也是研究的热点[6]，张桂梅等[7]利用轮廓分割点构建局部小波描述子，实现目标被局部遮挡或缺失情况下的识别；王斌[8]利用轮廓的全局和局部层次结构特征构建形状特征集，利用两个特征集实现目标识别，此外，轮廓的周长、面积、曲率、凹凸性、拱高函数也广泛应用于目标的定位识别中[9]，但是，当目标被局部遮挡时，大部分算法性能受到限制，无法准确对遮挡情况下的目标进行精确定位。

基于深度学习的目标定位检测与识别成为主流方法，此类算法比较知名的有R-CNN[10]、Fast-R-CNN[11]、Faster-R-CNN[12]、YOLOv3[13]、SSD[14]，这些算法相对于传统的方法，精度高，对遮挡、噪声、光照有较强的鲁棒性，但是训练时所需要的空间大、检测效率低、定位精度依赖于训练模型的精确度，极大限制了其应用，因此，使用传统的方法研究目标在局部遮挡条件下的定位具有十分重要的意义，所以，提出了局部遮挡条件下的普通工件定位检测算法，该算法具体步骤包括：①图像预处理；②轮廓角点检测；③构建几何哈希表；④目标匹配；⑤目标定位。

1 图像预处理

使用工业相机采集图像时，受周围生产环境的影响，图像中包含大量噪声，严重影响到算法结果，因此，采用高斯滤波算法去除图像中的噪声点，同时对图像进行直方图均衡化，增强背景和目标对比度，并采用大津法(OTSU)和形态学处理算法对图像进行二值化，对工件进行分割。基于分割图像，采用轮廓追踪算法提取图像中的轮廓信息。

2 轮廓角点检测

为了提高算法的鲁棒性，需要对轮廓进行多边形近似，使用轮廓角点特征近似描述目标轮廓。由于Douglas-Peucker算法[15]采用了一种计算点到直线的最大距离来寻找轮廓角点的方法，能对轮廓形状进行有效近似，因此采用该算法对轮廓进行多边形近似，提取轮廓角点特征。算法步骤如图1所示。

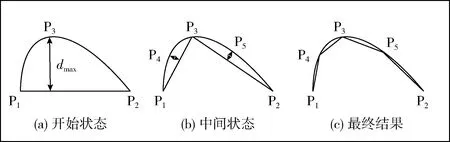
图1 Douglas-Peucker算法

对于闭合轮廓，首先选择轮廓中距离最远的两个点为起始点P1(x1,y1)和P2(x2,y2)建立一条直线，利用式(1)计算轮廓上任意一点P3(x3,y3)到该直线的距离d，找到距离直线距离最大(大于固定阈值)的轮廓点P3(x3,y3)，然后对P1P3、P2P3进行上述相同的操作，最终结果如图1(c)所示

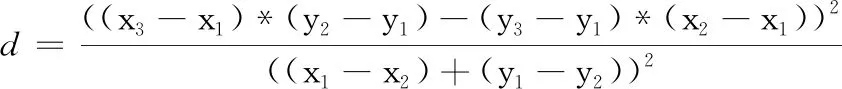
(1)

通过上述方法可有效提取出轮廓角点。

3 构建几何哈希表(hash table)

哈希表，又称作散列表，是根据关键码值可直接访问的数据结构，使用哈希表可极大提高目标查询效率。为了提高在线过程中目标的匹配效率，在离线过程中，使用轮廓角点构建关键码值，计算形状描述子构建模板信息，利用几何哈希表存储所有的模板信息。

3.1 关键码值计算

基于提取的轮廓角点特征，选择3个轮廓角点构建三角形，利用其几何元素(两边及其夹角)构建关键码值，示意图如图2所示

F=[L1,L2,∂1]

(2)

式中：L1为最大边长，L2为最小边长，∂1为两边夹角。

3.2 构建形状描述子

为了使构建的形状描述子具有平移、旋转不变性，利用轮廓角点特征建立局部坐标系，计算轮廓点在局部坐标系下的坐标构建形状描述子，原理如图2所示。

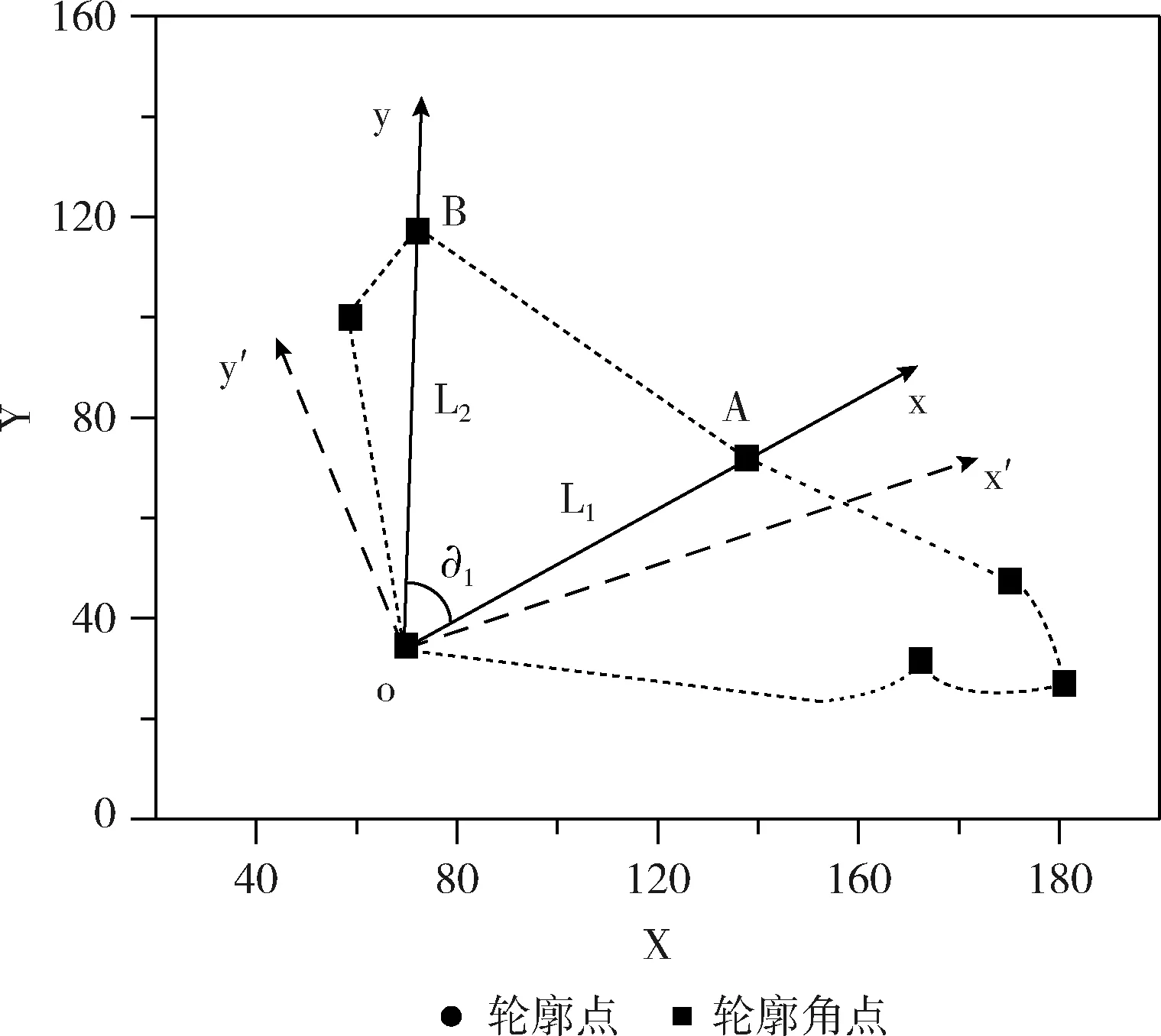
图2 构建直角坐标系

由于相邻轮廓点在局部坐标系中的坐标差异很小，且轮廓点个数多，在匹配过程中可能出现一对多的情况，为了解决该问题以及降低离线构建hash表过程的复杂度，设计以一定的步长对模板轮廓进行重采样，使用式(3)计算采样后的轮廓点坐标，构建形状描述子

(3)

式中：Xi、Yi、Xj、Yj是直角坐标系的基底信息，α、β是轮廓点Pr(Xr,Yr)在局部坐标系的坐标。

重复以上过程，记录由轮廓角点计算的所有的关键码值和形状描述子构建几何哈希表，完成离线模板模型的学习过程，结果见表1。

表1 几何哈希表

表1中，F表示关键码值，(xmN,ymN)表示第m个轮廓点在第N个局部坐标系中的坐标。

4 目标匹配

为了使算法对局部遮挡情况下的定位有较高的鲁棒性，设计在线过程中，任意选择3个实测角点特征构建实测关键码值，计算实测描述子信息，利用该码值对hash表中的模型进行地址查询，获取关键码值在hash表中的地址，利用投票机制和实测描述子对该地址下的模板描述子进行投票，若投票得分大于固定阈值，则实现匹配，否则，重新选择3个轮廓角点重复以上过程，若由实测角点构建的所有关键码值在哈希表中都不存在对应的码值，说明该目标不是待检测的目标。

4.1 地址查询

假设实测关键码值为Fj=[L1j,L2j,∂1j]，哈希表中关键码值为Fi=[L1i,L2i,∂1i]，采用式(4)计算码值间的最佳相似度，利用相似度进行地址查询

(4)

由于存在计算误差，当最佳相似度小于固定阈值(本文设置为0.5)时，说明哈希表中存在与实测码值对应的关键码值，获取该码值在哈希表中的地址索引i。

4.2 投 票

根据获取的地址索引i，对Fi对应的形状描述子进行投票。利用式(5)计算模板形状描述子中的每个元素与实测形状描述符号元素的相似度，若相似度小于固定阈值(本文设计为1)，则这两个点是匹配点。以上过程实现了模板轮廓和实测轮廓的粗匹配

(5)

式中：(xmi,ymi)是第m个轮廓点在第i个坐标系中的坐标，(Xj,Yj)是实测描述子第j个点在当前直角坐标系下的坐标。

为了有效显示投票结果，体现实测目标的遮挡情况，本文设计投票得分函数对其进行定量描述，利用得分函数显示匹配的结果，其函数如式(6)所示

(6)

式中：Num是匹配的个数，iSumNum是模板轮廓重采样后轮廓点个数。

得分函数值的大小近似地显示了实测目标被遮挡的程度以及模板轮廓和实测轮廓的匹配程度，当得分函数值大于固定阈值(本文设计为0.4)时，说明目标存在，匹配成功。

5 目标定位

为实现待检测工件的精确定位，需要根据获得的匹配点计算模板轮廓和实测轮廓之间的几何变换模型。基于得到的轮廓匹配点，利用最小二乘原理[16-18]和Turkey权重函数，通过迭代计算仿射变换参数；利用得到的模型参数对模板原始轮廓点进行仿射变换以实现目标的精确定位。

5.1 Turkey权重函数

Turkey权重函数是一种根据距离大小分配权重的函数，函数定义为

(7)

式中：δi为某点到模型的距离；τ为消波因子，表示用户所设定的距离。

由式(7)可知，差值过大的点则完全被忽略，差值越小则权重越大，由此将匹配误差较大的点对的影响降低到最低，差值过大的点是根据消波因子进行划分的，因此消波因子的选取对差值过大的点有较好的鲁棒性， 其大小设置为

τ=2*σδ

(8)

为了得到对离群值而言鲁棒的标准偏差， 一般情况下

(9)

5.2 基于Turkey权重函数求解仿射变换模型

假设模板轮廓点集为P={Pi|i=1,2,3,…,n}，实测轮廓点集为Q={Qi|i=1,2,3,…,n}；Pi和Qi为匹配的轮廓点对，这两个点集存在仿射变换，基本原理如式(10)所示

(10)

式中：a11、a12、a21、a22、Δx、Δy为模型参数。

为了计算点集Pi、Qi之间最佳的仿射变换模型参数，需要将匹配的误差平方和最小化,即

(11)

然而，由于不用轮廓点的匹配结果对模型参数的影响不同，为了提高匹配精度高的点对模型参数的贡献率，降低匹配精度低的点对模型参数的影响，引入了Turkey权重信息，根据不同匹配点的匹配误差赋予不同的权重，则模型的匹配误差平方公式和为式(12)

(12)

式(12)中

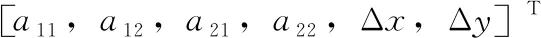
(13)

为了使得ε(X)的值最小化，获得参数X的最优解，根据极限原理，令偏导数为零

(14)

经整理和计算可得下面的等式：AX=B，其中

(15)

O3*3=C3*3=0

(16)

(17)

(18)

式(18)中,xi、yi是点集P中Pi的坐标，Xi、Yi是点集Q中Qi的坐标。

经计算，当模拟数据不全为0时，行列式|A3*3|≠0，因此

(19)

由于|A|不为零，所以矩阵A是可逆矩阵，便可获得几何变换模型参数X=A-1B的值。

在首次拟合时，并没有可利用的轮廓点对的匹配误差，因此，认为所有轮廓匹配点对模型参数的影响相同，权重均为1，从而获得近似的几何变换模型；基于该变换模型计算轮廓匹配点对的匹配误差。在每次迭代完成后，都需要根据轮廓点对的匹配误差更新权重。为了加速算法收敛速度，根据轮廓点对的权重信息和误差信息，将权重为零且误差大于固定阈值(本文设计为1)的匹配点剔除，实现精匹配，同时根据式(20)计算相邻两次迭代的均方差，给定阈值ε，当|dk+1-dk|<ε时迭代终止

(20)

通过上述原理便可获得模板轮廓和实测轮廓间最佳的几何变换模型。

基于得到的仿射变换模型，利用式(10)对原始的模板轮廓点坐标进行几何变换，实现目标精确定位。

6 实验结果

6.1 Turkey权重函数分析

为了验证Turkey权重函数可以有效地降低匹配较大的点对模型精度的影响，提高拟合结果精度。设计采用基于Turkey权重函数的最小二乘拟合算法和最小二乘拟合算法对已有的直线拟合数据和圆拟合数据进行直线和圆拟合，通过拟合结果对比，体现Turkey权重函数在模型拟合方面的优越性。结果如图3、图4所示。

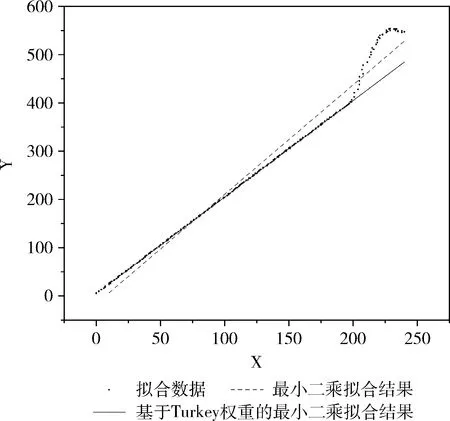
图3 直线拟合结果对比

图4 圆拟合结果对比

图3、图4结果表明，基于Turkey权重函数的最小二乘拟合结果明显优于最小二乘的拟合结果，因此，利用基于Turkey权重函数参与模型拟合，可充分考虑不同拟合数据对模型精度的影响，根据拟合数据对模型的贡献率赋予不同的权重，提高模型拟合精度。

6.2 基于Turkey权重函数求解仿射变换模型方法原理可行性分析

为了验证基于Turkey权重函求解仿射变换模型方法原理的有效性，设计模拟点集A(250个点)，对点集A中的点进行角度旋转、平移、尺度变换并加入随机误差构造点集B，利用本文算法和RANSAC[19]算法计算点集A、B之间的仿射变换模型，通过两种算法结果对比以及对参数的迭代变化进行深入分析，验证算法的可行性和有效性。其实验结果如图5所示，参数的迭代变化如图6所示。

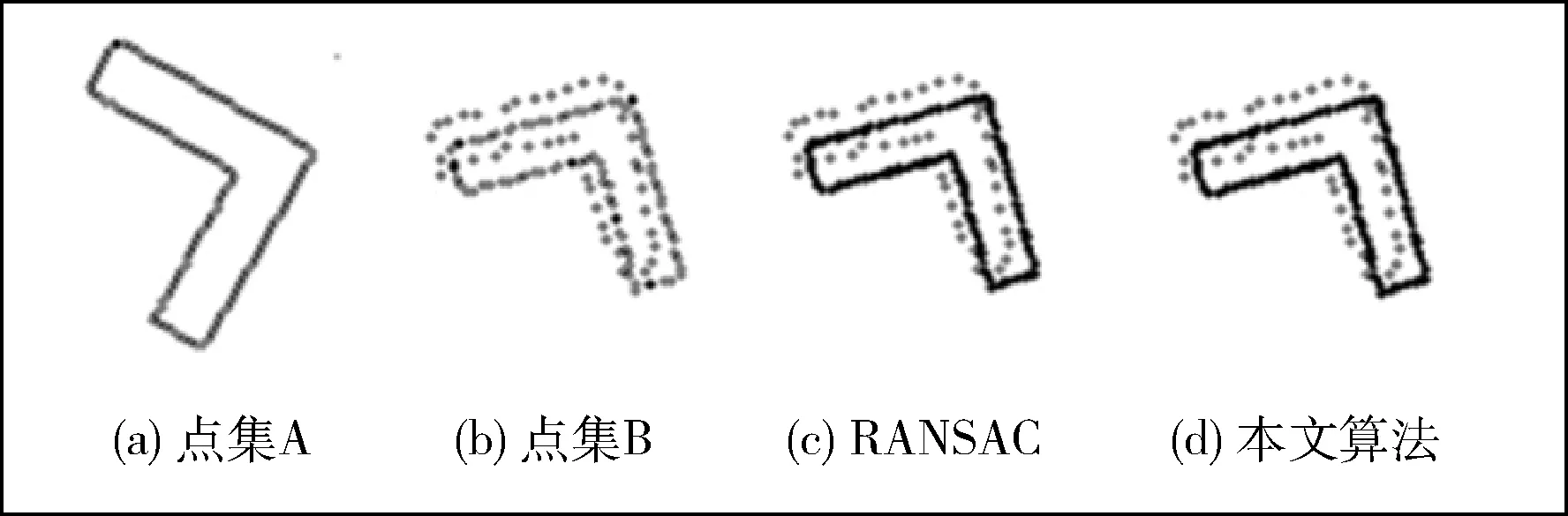
图5 仿射变换模型算法对比

图5是求解仿射变换模型算法结果对比图，从图中可以看出，两种算法均可正确的计算出点集间的仿射变换参数。图6显示了点集中匹配的轮廓点个数和均方差的迭代变化，可以看出，随着迭代次数增加，点集中适应度较差的点对被有效剔除，模型精度迅速提高，模型收敛速度加快；当点集中的匹配点不再发生变化时(迭代次数为5时)，模型精度变化幅度降低，逐渐收敛。同时，表2显示了两种算法的拟合结果，结果显示，在发生平移，旋转时，本文算法性能优于RANSAC算法。

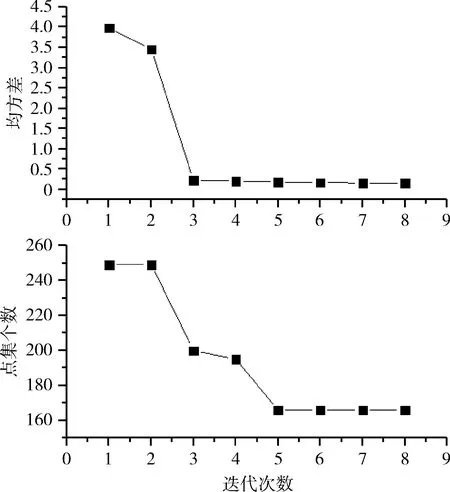
图6 参数迭代变化过程

表2 算法拟合结果对比

6.3 基于Turkey权重函数求解仿射变换模型方法时间可行性分析

为了验证基于Turkey权重函数求解仿射变换模型方法的高效性，设计当迭代次数为15且保证迭代结果收敛时，利用该方法分别对不同大小的匹配点集进行模型计算，统计计算各个点集的仿射变换模型参数所用的时间，通过统计的时间结果对比验证该方法的高效性。结果如图7所示。

结果显示，计算仿射变换模型所消耗的时间随着点集个数的增加缓慢增加、其效率受点集个数影响较小，且所用时间均在毫秒内，因此，该方法可以高效的计算仿射变换模型，满足实际需求。

6.4 目标定位检测

表3中：a11、a12、a21、a22、Δx、Δy是模型参数；Num是粗匹配的轮廓点个数;iNum是精匹配的轮廓点个数；Score是精匹配后的得分函数；ε(X)是模型精度。

为了验证算法的有效性，分别对两种普通工件进行定位识别。一种是具有规则几何形状的工件，如图8中的模板1所示，一种是具有不规则几何形状的工件，如图8中的模板2所示。通过对实测图像中的每个轮廓进行轮廓角点特征提取，构建实测关键码值和实测形状描述子，利用投票机制对hash表中的模板信息进行投票，实现目标匹配；基于匹配的轮廓点对，利用Turkey权重函数和最小二乘平方差原理计算匹配点对间的仿射变换模型，实现目标的精确定位。实验结果如图8所示，结果表明，当工件被局部遮挡且发生不同角度旋转、平移变化时，均能实现目标精确定位。同时，表3数据显示，在粗匹配过程中，可获取大量匹配正确的轮廓点，经过精匹配，剔除少量匹配误差较大的点；其匹配得分函数值可近似表达目标的遮挡程度，得分值越小，工件被遮挡越严重，实验精度表明，本文算法可获得精确的几何变换模型，实现目标的精确定位。

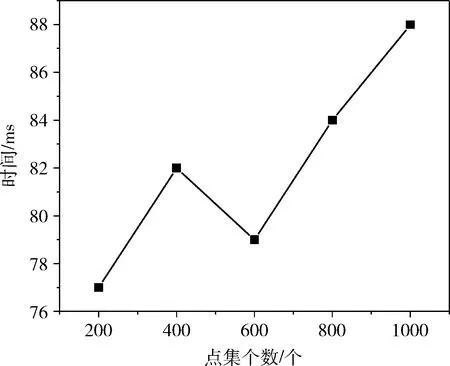
图7 时间统计结果

为了进一步说明算法的有效性，对多幅图像中不同遮挡情况下的工件进行识别，实验结果如图9、图10所示，结果表明，本文算法可实现目标在不同遮挡情况下的目标定位。

表3 实验结果统计

图8 普通工件定位结果

图9 规则工件定位结果

图10 不规则工件定位结果

7 结束语

为了有效解决普通工件在遮挡情况下，且发生任意角度旋转、平移时能精确定位，提出了局部遮挡条件下的普通工件定位检测算法，该算法在离线过程中，利用轮廓角点特征计算关键码值和形状描述子构建hash表，在线过程中，利用投票机制实现工件粗匹配，基于Turkey权重函数和最小二乘平方差原理求解模板轮廓和实测轮廓间的仿射变换模型，实现精匹配，进而实现目标精确定位。实验结果表明，本文算法在目标被局部遮挡，且发生平移、旋转时，能实现目标的精确定位，充分显示本文算法的优越性；但是该算法的时间复杂度取决于多边形拟合的结果和遮挡情况，当拟合得到的分割点越多、遮挡越严重， 则算法的执行效率越低，同时对实测轮廓进行多边形拟合时必须获取至少3个可以匹配正确的分割点才能实现目标的匹配，这是该算法的不足。