考虑新能源出力波动的火水电机组一次调频参数优化

贾庆岩，盛 举，孙建军

（1.国网湖北省电力有限公司电力科学研究院，湖北 武汉430077；2.武汉大学电气与自动化学院，湖北 武汉430072）

0 引言

一次调频指电网频率偏离额定值（50 Hz）时，负责调频的各机组自动地控制有功的出力，以稳定电网频率变化的自动控制过程。一次调频是动态的保证电网有功功率平衡的自动控制手段之一，目前主要参与电网一次调频的有火电机组、水电机组等［1-3］。在发电机组投运前，既要研究机组灵活性运行的安全性、经济性，环保性［4-5］，还需要研究一次调频系数的优化设置，确保并网机组在电网频率发生波动时能够快速准确地做出调节响应。

一次调频控制参数的合理优化设置，直接决定了一次调频控制性能的有效性和调节能力的强弱。作为最重要的一次调频控制参数，调速器转速不等率的选取和调频死区的设置直接关系着一次调频的响应速度及出力情况［6-8］。

能源互联下，风电、光伏等新能源发电出力具有较强的随机性和波动性［9-10］，这些新能源入网运行，增加了电网负荷波动规律的复杂性［11-12］，传统的一次调频试验中，往往只给出简单的阶跃负荷扰动或频率扰动［13］，没有考虑新能源出力的波动规律。

目前，对于调频死区传统的设置基本采用固定的±0.033 Hz（±2 r/min）的统一简单化设置。文献［14］通过相平面法对含有死区的电力系统一次调频模型进行了分析，但只考虑了单机系统；文献［15］通过分析单机等值系统中调速器死区对频率振荡的影响，得出无阶跃死区的设置与低频振荡的关系，但没有得出具体的死区设置范围；文献［16］基于粒子群算法，以经济型为目标一次调频，证明了死区设定方法可以有效地减少一次调频费用，但是没有给出具体的转速不等率和死区设定参考值；文献［6］以总煤耗量以及总污染排放最低为目标函数的最优化模型，找出了最佳速度不等率的设定方法，但没有考虑调频死区的设定方法；文献［17］对一次调频中的随机过程进行了分析，但没有考虑具体的负荷数据的波动情况。文献［18］将调速器死区通过描述函数法线性化，研究了考虑死区的两区域互联电力系统调频过程。上述文献集中在建立一次调频数学模型，以简单的负荷阶跃扰动过程作为一次调频的分析过程。考虑新能源出力情况下的负荷波动情况，对一次调频系数的优化选取十分重要。

本文在以电网稳定运行的条件下，考虑负荷，新能源出力波动分布特征，提出考虑经济性，环保性的发电机组一次调频优化概念。建立了一次调频的仿真模型，并采用粒子群算法对其参数进行优化，结果表明基于粒子群算法的以经济性和环保性为目标的一次调频参数优化方法是有效的。在确保电网频率安全的前提下，积极响应节能减排的政策号召，探索一次调频中的环保性、经济性和稳定性。

1 调速系统等值频率模型

1.1 用于一次调频分析的模型

一次调频过程的主要研究对象是电力系统惯性中心的频率。本文认为发电机之间严格保持同步运行，发电机间的相对摆动可以忽略不计，进而将同类型的多台发电机组等效为一台机组［19］。

对于参加一次调频的机组，主要分为凝汽机组（非再热）、再热机组两大类。本文主要考虑这两类机组还有水电机组参与电网一次调频的情况［20］。

对于凝汽式汽轮机组，其传递函数为：

式（1）中，Ts为调速器油动机时间常数，TVH为原动机容积时间常数；

对于再热机组，其传递函数为：

式（2）中，TRH为再热容积时间常数；αH为高压缸功率占整个汽轮机功率的份额；

对于水轮机组，其传递函数为：

式（3）中，KD，KP，KI分别为调速器的比例、积分以及微分系数；TW为水流惯性时间常数；TG为伺服系统的时间常数；bp为永态转差系数。

本模型认为所有机组参与电网一次调频，且电网一次调频负荷已经分配完成，凝汽式汽轮机、再热式汽轮机占整个电网的总发电份额均为40%，水轮机组的发电份额占整个电网的总发电份额为20%。

模型如图1所示，图中αN，αR，αH分别为凝汽式汽轮机组，再热式汽轮机组，水轮机组在电网中的装机容量/电力系统装机容量；δN，δR，δH为凝汽式汽轮机组，再热式汽轮机组，水轮机组的转速不等率；ΔPL为负荷扰动（标幺值）；TaΣ为整个电网的转子时间常数，βΣ为负荷频率特性系数；Δf 为整个电网的频差（标幺值）；ΔPTN，ΔPTR，ΔPTH分别为三类机组的输出功率偏差值［21-25］。

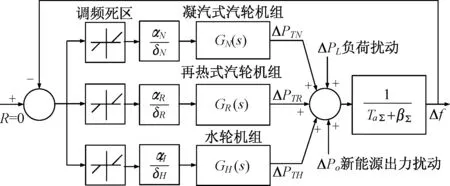
图1 分析一次调频过程的同步发电机组并行的数学模型Fig.1 Mathematical model of synchronous generators used to analyze the process of power system primary frequency control

1.2 速度不等率

《GB/T 31464 电网运行准则》给出了火电机组速度不等率设置范围为4%～5%；水轮机组不大于4%。机组并行时，速度不等率的设置不宜过小也不宜过大，如何设置各机组的速度不等率对一次调频的经济性和调频的合格率影响很大［6，26］。

1.3 调频死区

1）《Q/GD W669 火力发电机组一次调频试验导则》等标准中给出了调频死区的设置范围，一般要求火电机组不大于±0.033 Hz 或者±2 r/min。在工程实际中，发电机组的调频死区基本均设为±0.033 Hz（或2 r/min）。水电机组的调频死区基本均设为±0.05 Hz。死区环节的存在，使得系统的强非线性特征更加明显，并削弱一次调频的能力［21-23］。

一般调速器死区是一个具有滞后型的非线性问题，无阶跃死区目前应用最为广泛，又称普通型调速器死区［15］，如图2 所示，其中a 为转速死区大小，Δn 为转差。

图2 普通型调速器死区Fig.2 Dead band without step

2）死区对频率震荡的影响

图3 为考虑死区的单机等值系统，开环传递函数为调速器、原动机、发电机传递函数的乘积。

图3 含死区的单机一次调频模型Fig.3 Model of single generator primary frequency regulation with deadband

由于发电机、原动机、调速器构成的系统往往包含惯性环节，因此具有较好的低通滤波性能，满足采用描述函数法进行分析的条件。其中，3 个部分组成的开环传递函数为：

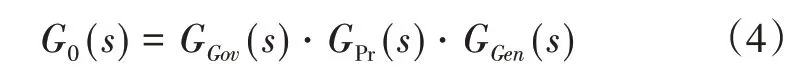
死区环节用描述函数表示：

描述函数法通过复平面上G0(jω)曲线和死区环节1/N(A)曲线之间的相对位置分析系统稳定性。

采用典型数据，分别画出3 种发电机组的单机一次调频系统对应的开环传递函数频率特性与死区环节的负倒特性的奈奎斯特图如图4。

其中图4（a）、图4（b）对应的凝汽式和再热式机组的奈奎斯特特性图中的G0(jω)没有包围-1/N(A)，则整个非线性系统是稳定的。

图4（c）对应的水轮机组原动系统出现负阻尼特性导致G0(jω)与-1/N(A)交叉，处于渐进稳定状态，根据1.1 节的具体水轮机模型和奈奎斯特稳定性判据［15］，可以确定水轮机组调速器死区在一定范围内，即：

2 负荷与新能源出力波动特征

图4 三种发电机组的单机开环频率特性和死区负倒特性Fig.4 Open loop frequency characteristics and minus reciprocal of deadband of three kinds of generators

本文选取了湖北省某区域一年中289天的测得有功负荷数据，采样周期为15 min/次，目前一次调频动作频率大约为10 min/次，通过统计该区域负荷波动特征，得到符合实际的阶跃扰动情况。

另外，本文选取了该区域365 天的风电和光伏出力的数据，采样周期也为15 min/次，统计分析新能源出力的波动特征。

2.1 负荷聚类与波动特征

将负荷数据归一化后，根据日负荷的总体特征，将289 天的日负荷数据进行聚类处理。本文采用Kmeans聚类方法［27］，将289天的数据聚类为3类，即3种典型场景。

这3类日负荷曲线对应3种典型场景，3类场景对应的数量如表1所示。针对这3类场景，研究其负荷波动情况。

表1 负荷曲线场景分类Table 1 Daily load curve scene classification

统计3 类场景的负荷波动分布情况，根据拟合度发现基本满足正态分布的规律，如图5。

图5 三种典型场景负荷波动统计Fig.5 Three typical scene load fluctuation statistics

一般的负荷扰动值分布在0.01 p.u.到0.05 p.u.之间，以0.01 p.u.为区间，在极少的情况下才会出现高于5%的负荷扰动，大多数情况下的负荷扰动都处于3%以下。由统计拟合结果得出对应3种典型场景负荷扰动的概率分布组合情况，如表2、表3所示。

表2 负荷波动统计与拟合Table 2 Load fluctuation statistics and fitting

表3 负荷阶跃扰动的概率组合Table 3 Probability combination of load step disturbances

2.2 风电波动特征

风机的出力波动统计如图6 所示，用非参数统计（non-parametric statistics）方法进行拟合。

图6 风机出力波动统计Fig.6 Wind turbine output fluctuation statistics

以0.01 p.u.为区间，统计拟合结果得出对应风机出力阶跃扰动的概率组合情况，如表4所示。

表4 风机出力阶跃扰动的概率组合Table 4 Probability combination of Wind turbine output step disturbances

2.3 光伏波动特征

光伏发电的出力波动统计如图7 所示，因为光伏出力的特殊性，去掉了出力为0的情况，用非参数统计（non-parametric statistics）方法进行拟合。

图7 光伏风机出力波动统计Fig.7 PV output fluctuation statistics

以0.01 p.u.为区间，统计拟合结果得出对应风机出力阶跃扰动的概率组合情况，如表5所示。

表5 光伏发电出力阶跃扰动的概率组合Table 5 Probability combination of PV output step disturbances

3 系数优化模型

3.1 煤耗模型

火电机组的煤耗量特性模型可拟合为：

式（7）中，i = 1，2，…，M，αi、βi、χi为机组的煤耗特性系数；Pi为第机组的实时功率（kW），Ci(Pi)为机组的实时煤耗值（t/h），为了让煤耗量最低，目标函数为［4，26］：

3.2 污染物排放量模型

火电机组的污染物排放模型可拟合为：

式（9）中，i = 1，2，…，M，ai、bi、ci、di为机组的污染物排放特性系数；Pi为第机组的实时功率（kW），Wi(Pi)为机组的实时污染物排放量（mg/h），为了让污染物排放量最低，目标函数为［6，26］：

3.3 一次调频积分电量

一次调频积分电量考核方法电网对机组一次调频的考核包括两个方面：并网机组一次调频功能是否正常投入；一次调频动作的积分电量是否满足电网要求［28］。

一次调频理论积分电量：

一次调频实际积分电量：

一次调频积分电量评价指标：

3.4 统一目标函数

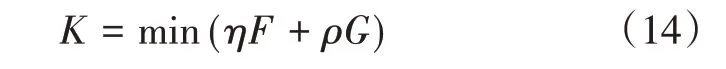
式（14）中，η 为燃煤成本（元/t），为了让两者处于同一量纲上，后者还要乘以ρ这一系数。

3.5 考虑负荷和出力扰动

式（15）中，KΔP=-0.01为负荷扰动为ΔP =-0.01时目标函数；μΔP=-0.01为负荷扰动为ΔP =-0.01 时的概率系数；Kσ为综合目标函数。

3.6 约束条件

1）发电机组一次调频容量限制

各种发电机参与频率调节只能在各自的出力范围内调整，有如下出力约束：

2）机组一次调频稳定后频差要求

电力系统中常常为了保证系统频率的稳定性要求，规定了电力系统频率的标准为50 Hz，而其频率偏差不应该超过±0.2 Hz，即：

3）一次调频积分电量评价指标

一次调频过程中，考察指标V 值必须在大于一定指标，即：

4）转速不等率范围

5）调试器死区范围

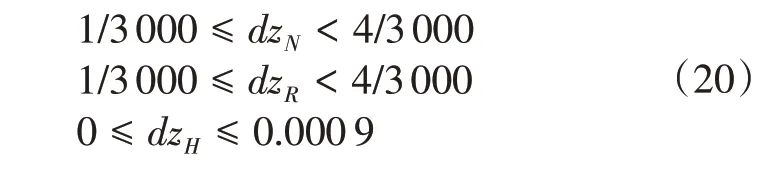
4 优化算法实现过程

4.1 粒子群优化算法

设粒子群规模为500，粒子群繁殖的代数为100，搜索空间维数为6，区域电网一次调频仿真模型如1.1节的图1所示。根据算法具体运行步骤可以得到其计算过程的流程图［29］，如图8所示。

图8 优化算法流程图Fig.8 Optimization algorithm flowchart

初始状态该区域电网的汽轮机组调频死区均设为±0.033 Hz，调差系数均设为0.05。负荷扰动为阶跃扰动，为了符合实际情况，加上了负荷随机扰动，采用了随机信号模型［30］，如图9所示。

图9 负荷随机扰动模型Fig.9 Load stochastic perturbation model

4.2 适应度函数

θ(k)为惩罚因子，其初值根据实际要求选取，此处取正无穷；ξn为第n 个场景的出现概率，Kn，σ为第n 个场景的适应度函数，K∑为最后综合的适应度函数。

4.3 仿真验证

在MATLAB/Simulink 中搭建仿真模型，系统参数为典型数据：Ts= 0.2 s，TVH= 0.2 s，TRH= 9 s，Ta= 8 s，KD= 3.33s，KP= 5.185s，KI= 0.988 s，TW= 1s，TG=0.2 s，bp= 0.04，αN= 0.4，αR= 0.4αH= 0.2，TaΣ= 12 s，βΣ= 1s，一次调频时间为20 s。

煤耗特性系数和污染物排放特性系数如表6、表7所示。

表6 煤耗特性系数Table 6 Characteristic coefficient of coal consumption

表7 污染物排放特性系数Table 7 Emission characteristic coefficient of pollutant

文献［16］指出，在负荷扰动较小（不大于0.01 p.u.）的情况下，区域电网的一次调频参数有较大的改进空间，经算法优化重新配置一次调频参数后能使系统运行时经济性得到很大的提升；而当负荷扰动较大（不小于0.05 p.u.）时，区域电网所设置的一次调频参数已经接近于最优的一次调频参数设置［16］。而本文通过概率组合的评估方式，能得到最合理的一组系数。表8为优化前的系数，表9为优化后的系数。

图10 显示了在负荷扰动为0.05 p.u.时，优化前后的电网频率，整个一次调频过程中，电网频率偏差均处于标准范围之内，优化之后，频率下降最低点从原先的49.8 Hz 改善为49.81 Hz，稳定频率值从原先的49.85 Hz改善为49.86 Hz，一定程度上改善了系统的频率响应过程。

表8 系数优化前Table 8 Initial coefficients

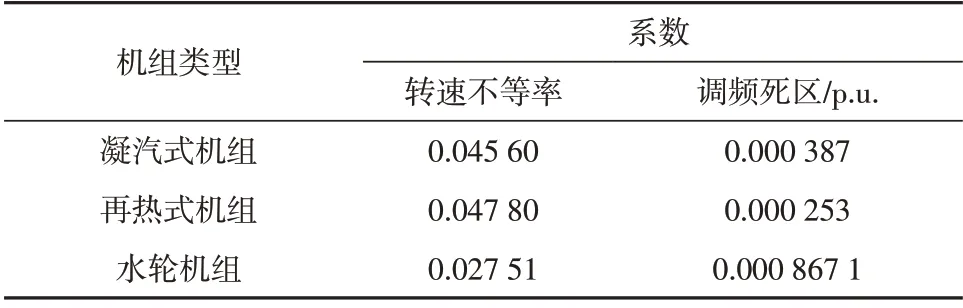
表9 系数优化结果Table 9 The result of coefficient optimization

图10 优化前后电网频率Fig.10 Frequency of grid before and after optimization

优化前后的煤耗和污物排放数据如表10所示，煤耗的优化率为1.98%，污染物排放的优化率为4.20%，符合预期目标。

表10 系数优化前后Table 10 Initial coefficients

5 结语

为了响应国家节能减排的号召，通过评估煤耗和污染物排放量来确定一次调频的系数行之有效。本文分析了系统在稳定运行下的一系列约束条件，并通过统计分析负荷波动的分布情况，提出了一种考虑负荷波动特征的一次调频系数设置方法。

1）为了确保系统的稳定正常运行，本文考虑的约束条件众多，一方面能够保证电网一次调频后稳定频率不超出电网安全范围，减少低频振荡过程；另一方面能最小化一次调频过程中的煤耗和污染物排放量，既保证绿色环保，又保证经济高效。

2）不同于以往只考虑单一简单的负荷阶跃扰动的情况，通过分析负荷波动情况，基于概率分布综合评估各种扰动情况下的一次调频过程。

3）建立电网一次调频的仿真模型进行验证，通过粒子群算法，获得一组最优的一次调频系数，为各机组系数的设置具有参考价值。

4）优化前后，一次调频的频率响应得到了一定改善，也有效地减少了煤耗与污物排放量。