电力系统新增黑启动机组优化布点研究

张永武，朱海南，张同军，王 涛，李丰硕

（国网山东省电力公司潍坊供电公司，山东 潍坊 261000）

0 引言

随着我国特高压交直流技术的快速发展，大区域电网互联逐步增强、清洁能源渗透率稳步提高，电力系统的动态特性发生了极大变化，电力系统的运行点越来越接近其稳定极限。在这种情况下，电网容易在级联故障条件下引发更大规模停电事故，不能满足社会可靠电力供应需求［1-3］。大停电事故发生后，应快速、安全、经济地恢复供电，最大限度地减小停电损失和时间、恢复控制措施，提高电网防御能力、降低失稳风险［4-5］。

系统发生停电事故后的恢复过程包括黑启动、网架恢复和负荷恢复3 个阶段，其中黑启动阶段是整个恢复过程的基础，其重要性不言而喻。在黑启动阶段，黑启动机组的数量和分布是非常重要的影响因素。合适的黑启动机组数量和分布能够极大加快系统的恢复进程，从而缩短电网恢复时间。许多学者对黑启动电源的选择和布点进行了研究。文献［6］提出并建立了电网黑启动方案评价指标体系，为电网黑启动电源布点和启动方案的评估提供参考依据。文献［7］提出了兼顾功率支持和恢复安全裕度的扩展黑启动方案多目标优化方法，综合考虑发电量、电压稳定裕度和节点电压水平，选取最优扩展黑启动优化方案。文献［8］分析了影响黑启动电源布置的因素，建立了以社会停电损失最小为目标的黑启动电源规划模型，优化黑启动电源的安装位置及容量，给新增黑启动机组的布点提供了一种思路。文献［9］提出了一种基于深度学习的机组恢复在线决策方法，该方法可获得具有较高鲁棒特性的恢复方案。文献［10］提出了机组布点方案的经济效益指标函数，利用具备快速切负荷机组的优异黑启动特性，对已有电厂进行快速切除负荷 （Fast Cut Back，FCB） 技术改造，分析了各项投资成本，计算经济性最优的FCB机组配置方案。但该方法不适用新增黑启动机组的情况。可以看出，现有研究侧重于对黑启动电源进行优选排序，简化处理系统恢复过程中各种约束条件，选择对应的求解算法，计算目标函数最优解，既最优黑启动恢复路径方案。然而，伴随着国内特高压交直流技术的快速发展，区域电网互联增强、清洁能源装机容量提高、各种特性负荷的接入，机组恢复过程受到越来越多外部不确定因素的影响，使得黑启动电源选择、恢复路径制定变得越来越难。为进一步提高系统恢复速度，有必要在系统中增设黑启动机组，新增黑启动机组的布点大多依靠运行经验来确定，缺乏定量分析手段和方法。

充分分析黑启动电源数量、分布、容量以及电网网架结构等因素对系统恢复过程的影响，提出电网坚强度的定义。以电网坚强度和新增黑启动机组投资成本为指标，量化分析最优黑启动机组布点位置，为电网黑启动电源规划布点提供量化参考，满足电网防御性和经济性实际需求。

1 电网坚强度影响因素

网络的坚强度定义为网络遭受攻击后能够快速恢复初始运行状态的能力。对于一个电力系统而言，电网坚强度则表示在电力系统发生大规模停电事故后，能够快速恢复到初始状态的一种能力。电力系统发生大规模停电之后，其恢复到初始状态的过程包括三个阶段：黑启动、网架重构和负荷恢复阶段［11-13］。

黑启动阶段： 电网利用事故后残存的发电机组或者具有自启动能力的黑启动机组，按照制定好的启动方案，给其他待恢复机组提供所需的启动功率，使其恢复发电能力并形成若干个独立子系统重新并入电力系统中。在该阶段，待恢复机组能否成功启动与多种因素密切相关，如系统中可用的黑启动电源容量、机组数量、机组分布等因素［14-16］。黑启动电源容量： 容量大的黑启动机组有利于提高系统恢复进程的速度，不仅能够满足待恢复机组启动所需的功率要求，还能为一部分重要负荷提供功率支持。黑启动机组数量：电网中具有多台黑启动机组时，可将电网划分为相互独立的若干分区，各分区内待恢复机组恢复发电能力后适时将该分区重新并入电力系统中，从而缩短整个恢复过程的耗时［17-18］。一般来说，具有黑启动能力的电厂无法满足同一电厂中多台黑启动机组同时启动的要求，因此同一电厂中各机组预先制定好启动次序，具备优异黑启动特性的机组应优先启动。

黑启动阶段完成之后，后续恢复过程分为网架重构阶段和负荷恢复阶段。网架重构阶段的任务主要是给系统中重要变电站（重要负荷）和部分输电线路进行充电，通过稳定可靠的输电线路将已经恢复的若干独立子系统进行互联，逐步恢复系统内的主干网架；负荷恢复阶段的任务是根据负荷的重要程度对负荷送电的次序优化，负荷功率增加的快慢应与机组出力相配合，保证电网频率、电压稳定。在这两个恢复阶段中，主要的恢复操作为恢复系统中的输电线路，坚强网架结构的恢复是决定恢复过程能否顺利进行的关键因素。

由此可以看出，在电力系统恢复过程中电网坚强度主要与以下因素有关：1）黑启动电源容量、机组数量、机组分布；2）黑启动机组的启动次序；3）电网拓扑关系既系统网络连接矩阵。

2 新增黑启动机组系统建模

2.1 数学模型

电网坚强度指标，反映了电力系统发生大规模停电后恢复到初始运行状态的能力，电网坚强度Str1定义为：

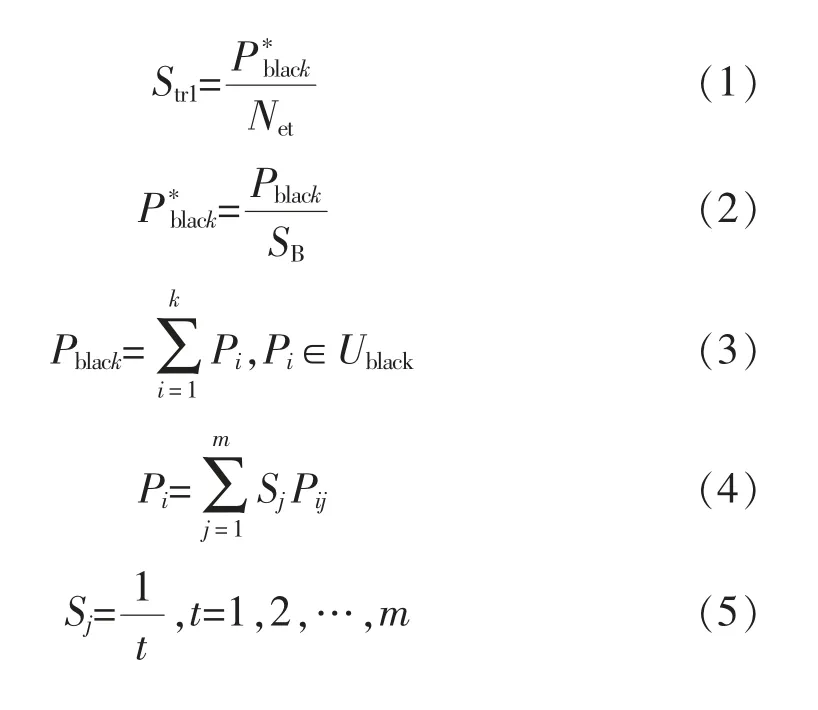
式中：Ublack为系统中含有黑启动机组的电厂集合；k 为Ublack中电厂个数；Pi为第i 个电厂中所有黑启动机组的加权容量和；m 为第i 个发电厂中黑启动机组的数量；Pij为第i 个发电厂中第j 台黑启动机组的容量；Sj为第i 个发电厂中第j 台黑启动机组的启动系数，其与黑启动机组j 的启动次序t 有关；Pblack为系统中所有黑启动机组的加权容量和；P*black为Pblack的标幺值；SB为选定的基准容量，基准值SB取为100 MVA；Net为网络中所有线路的平均长度，反映了按黑启动电厂数量将电网划分为若干分区后，黑启动机组功率输送到各个站点的难易程度，可用系统网络连接矩阵的平均值与具有黑启动能力的电厂数量的比值来表示；sum（M）为系统网络连接矩阵M中所有元素的和；L 为矩阵M 中不为0 的元素的个数。

系统网络连接矩阵M 表示黑启动机组与待恢复机组间或发电机组与系统负荷间的电气连接距离，数值上可采用输电线路的拓扑关系和对应的线路参数。系统所对应的加权网络连接矩阵M 为一方阵，并且行数与列数均等于系统中可用的厂站节点的数量。当系统中节点a 与节点b 之间存在可用的联络线lab时，记线路lab的电抗标幺值为xab，则连接矩阵M 中的元素Mab=Mba=xab；反之，若系统中节点a与节点b 之间不存在可用的联络线时，Mab=Mba=0。对于含有n 个站点的系统，其对应的连接矩阵M 为如下形式。

式中：对于任意元素Mab和Mba，存在Mab=Mba。

从电网坚强度公式可以看出： 黑启动机组的容量代表了系统恢复起始阶段的能力，黑启动机组容量越大，代表恢复能力越强，则该系统的坚强度越高；黑启动机组数量越多，系统划分为更多的独立分区，各分区内电网恢复速度越快，则该系统的坚强度越高；厂用负荷低、操作简单、爬坡率大的机组优先启动，系统恢复速度越快，稳定性越好，则该系统的坚强度越高；系统恢复过程的本质是及时将电力从黑启动机组逐步重新输送到其余站点的过程，整个系统的结构越紧密，电气距离越近，则重新恢复供电的难度越小，系统的坚强度越高。

当电网特性发生变化，预先编制的黑启动方案不满足系统快速恢复要求时，需要增加黑启动机组的数量。网络中确定可以新增黑启动机组的站点位置，组成候选集合G，设集合G 中包含g 个站点，这些站点可以是原有发电机组改造，也可以是原有变电站进行改造，或者是新建安装有黑启动能力机组的发电厂。新增黑启动机组后电网坚强度发生改变，分别为Str21，Str22，…，Str2g，对应变化量为ΔStr21，ΔStr22，…，ΔStr2g，计算公式为

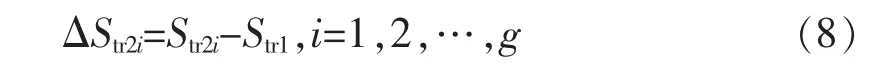
式中：Str1为新增黑启动机组前原电网的坚强度。

然而，提高电网坚强度势必会增加电网投资，在候选集合G 中的不同站点新增黑启动机组的投资成本是不同的，不合理的投入产出比也会影响电网经济效益。为统筹考虑电网安全防御性和经济性，在电网坚强度和投资成本之间作合理取舍，将机组投资成本纳入布点方案计算中，统计得到在G 中的g 个站点新增黑启动机组的投资分别为C1，C2，…，Cg。计算电网坚强度的变化量△Str2i与对应投资Ci的比值Pi为

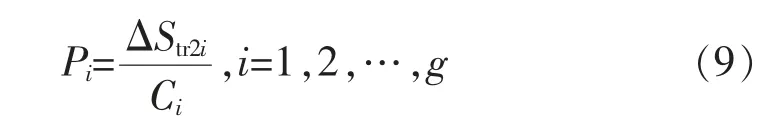
Pi值越大，表示单位投资带来的电网坚强度越大，相应机组的黑启动能力越强，网架构架和负荷恢复速度越快。

2.2 计算步骤

新增黑启动机组布点方法的计算流程如图1 所示。计算过程可分为如下步骤：

1）对电网网络结构进行分析，获取计算所用数据，并建立系统对应的加权网络连接矩阵M；

2）根据黑启动机组容量、启动次序、启动系数等条件计算新增黑启动机组前原系统的电网坚强度Str1；

3）在网络中选定新增黑启动机组的候选站点，组成候选集合G，共计g 个候选站点；

4）新增黑启动机组后电网坚强度发生改变，计算在不同站点新增黑启动机组后的电网坚强度Str21，Str22，…，Str2g。

5）根据式（8）计算电网坚强度的变化量ΔStr2i；并计算新建黑启动机组的投资成本Ci。

6）根据式（9）得出Pi，比值最大者即为最优的黑启动机组布点。至此，确定新增黑启动机组布点的计算过程结束。

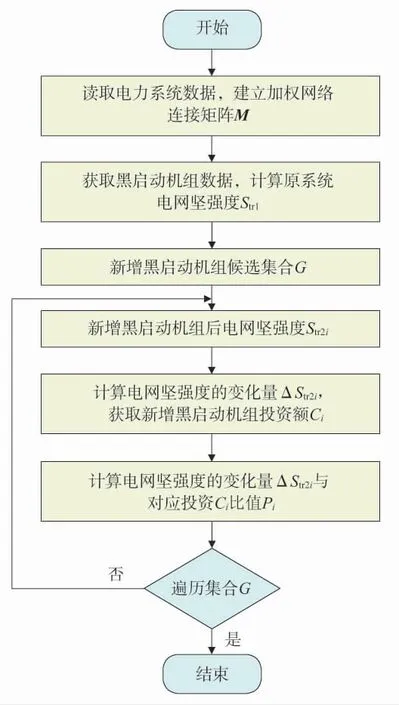
图1 计算流程

3 算例分析

以修改后的IEEE30 节点系统为例进行仿真计算，修改后的IEEE30 节点系统结构如图2 所示，设置本系统初始状态包含5 台黑启动机组，分别为节点1上的3台（1 号、2 号、3 号）发电机组和节点25 上的2 台（1 号、2 号）发电机组。黑启动机组容量和相应的启动顺序如表1 所示。节点2、13、22、23 和27 上的发电厂中机组均无黑启动能力，为待恢复机组。IEEE30 节点系统的电压等级为220 kV。

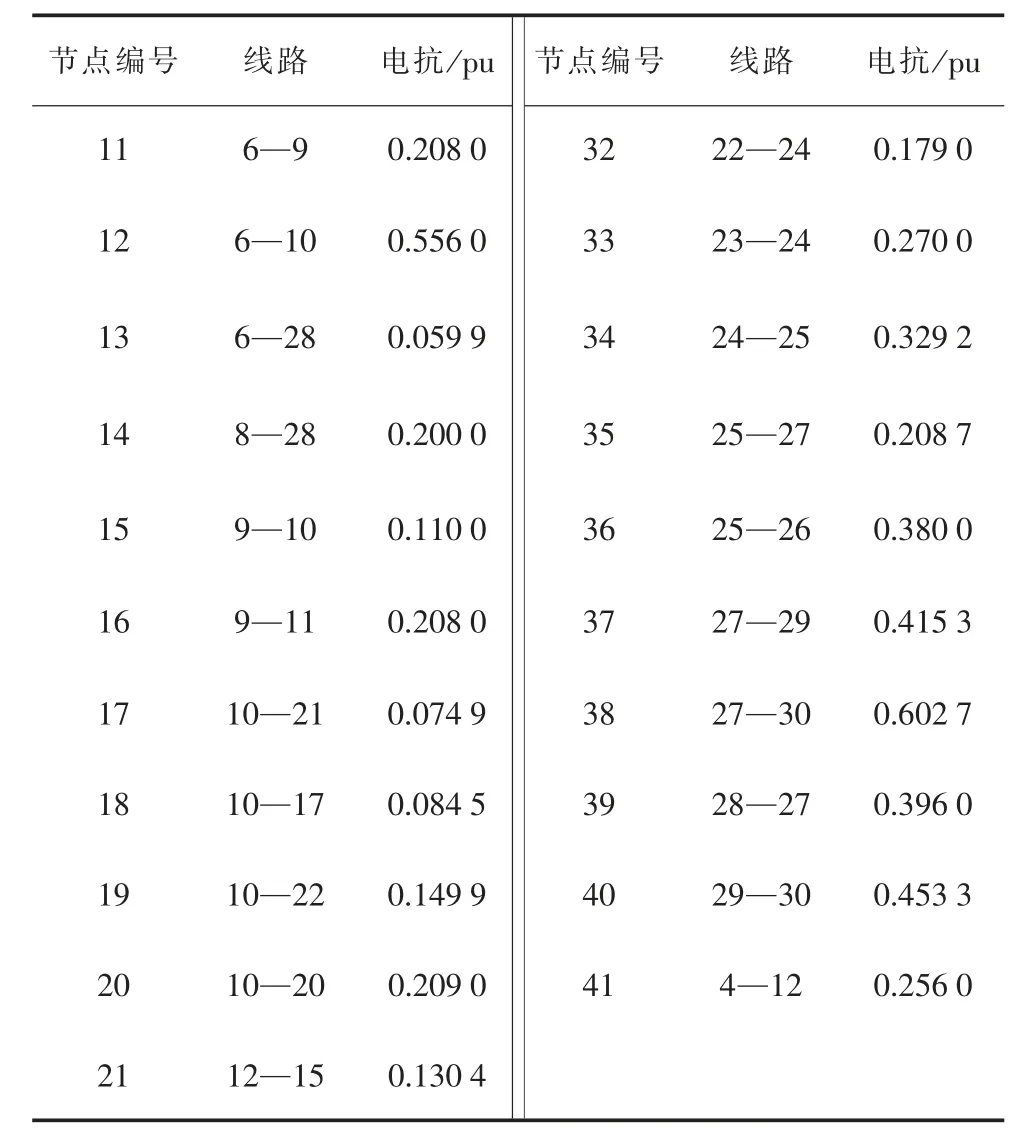
修改后的IEEE30 节点系统共包含41 条线路，根据输电线路的拓扑关系和对应的线路参数计算线路电抗值如表2 所示。

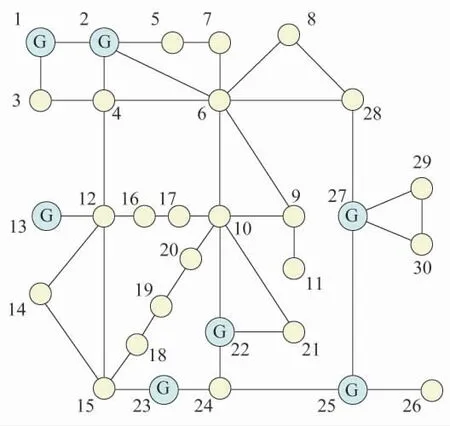
图2 IEEE30 节点系统结构

表1 黑启动机组容量和启动次序

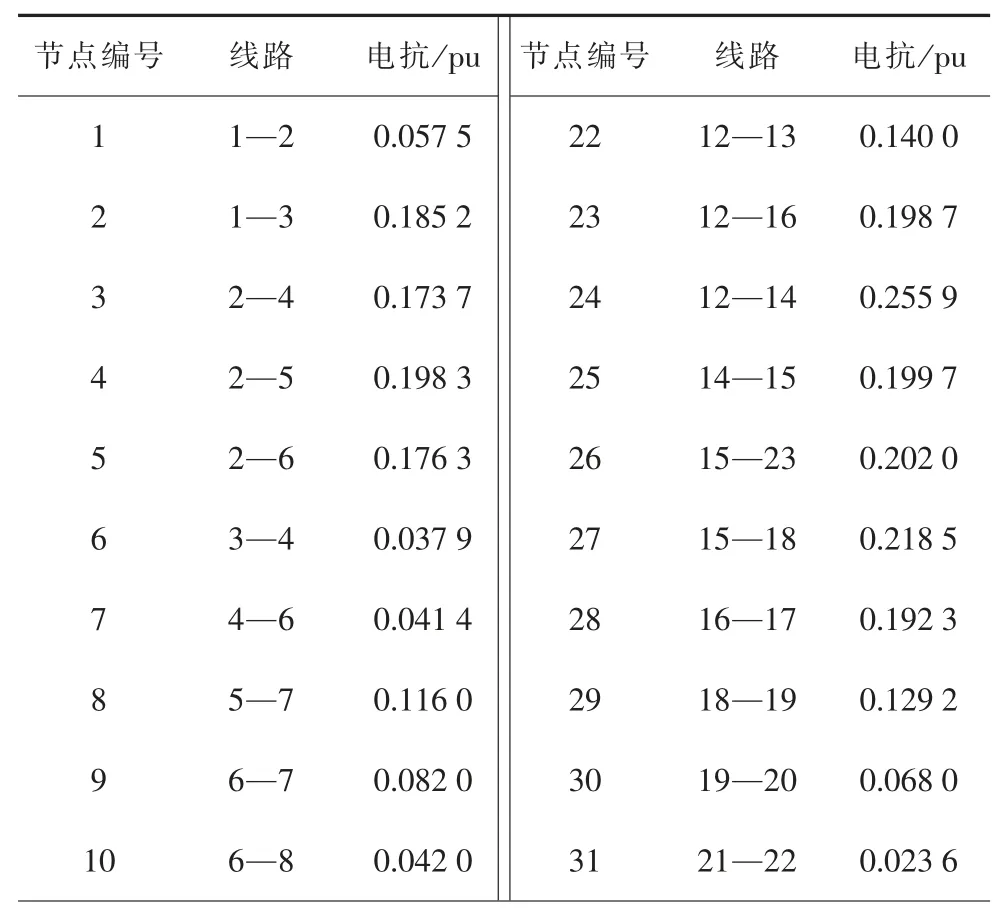
表2 IEEE30 节点系统线路参数

根据IEEE30 节点系统的拓扑结构和各条线路电抗的标幺值，建立IEEE30 节点系统对应的连接矩阵M。进一步求得新增黑启动机组前原电网的坚强度为

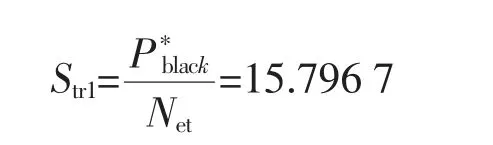
在该算例中，设定普通负荷站点无法新建黑启动机组，可以新增黑启动机组布点的站点集合G＝｛2，13，22，23，27｝。各站点新增黑启动机组的容量和相应投资成本如表3 所示。

表3 新增黑启动机组容量和投资成本

在G 中不同站点新增黑启动机组之后，电网坚强度变化量与投资额的比值P，如表4 所示。

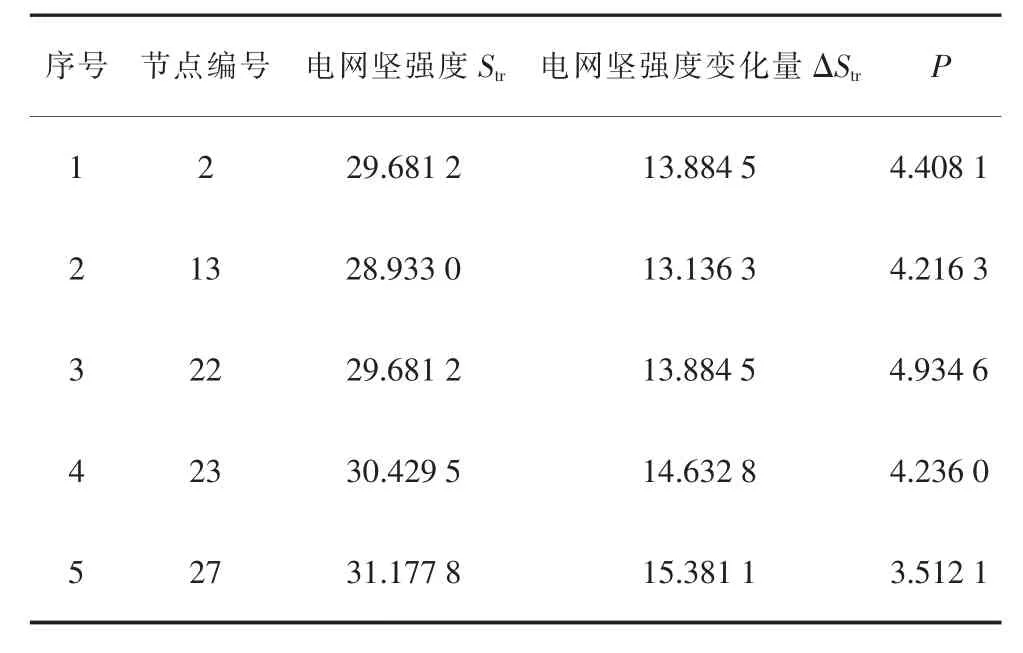
表4 新增黑启动机组后电网坚强度

从表4 可以看出，在节点22 新增黑启动机组对应的P 值最大，对整个电网坚强度的提升作用最为明显，是最优的布点位置。

4 结语

充分分析了黑启动电源的数量、分布、容量以及电网网络拓扑关系等因素对系统恢复过程的影响，提出了电网坚强度指标的定义，量化分析电网恢复能力大小，然后以电网坚强度和新增黑启动机组投资成本为限制条件，提出了新增黑启动机组最优布点的一种定量分析方法，以满足大电网风险防御性和经济性实际需求，同时也为现代电网电源规划提供了一种新的思路。以修改的IEEE30 节点系统进行验证分析，其计算结果表明本文所提方法的有效性和合理性。