黄河三角洲盐碱土微观孔隙特征的分形研究
李克升,刘传孝,李全新,耿雨晗
山东农业大学水利土木工程学院,山东 泰安 271018
土体的物理力学性质在很大程度上取决于其微观结构[1-5]。土体孔隙作为渗透的通道,其大小、分布和迂曲程度将直接影响土体渗透性[6]。因此,应用微观测试技术结合分形几何学理论来探索土体的微观孔隙特征,进而研究土体的物理力学性质是必要的。近年来,扫描电镜(SEM)、CT、压汞法(MIP)和能谱(EDS)等新技术的发展,给土体微观结构的研究提供了丰富的技术手段[7-9]。此外,国内外学者对分形几何学的进一步探索也为定量表征土体结构的复杂程度提供了理论依据。
国内外学者采用不同的微观测试手段和分形模型对不同土体的微观孔隙特征、土体结构的复杂程度和分形维数与微观参数的关系进行了深入研究,取得了大量的成果。Lu Y,et al.基于扫描电镜试验对冻融循环条件下黏性土的裂缝进行了分形几何研究,发现分形维数与表面裂缝率有良好的相关性[10]。Zhou J,et al.在分形和概率分析的基础上,建立了软粘土冻融效应综合双孔隙度计算模型,并对该模型的应用进行了探讨[11]。Atzeni C,et al.对多孔材料的孔隙结构采用Pfeifer 和Avnir 方法确定了实验数据集的分形维数,发现P 海绵模型比Menger 海绵模型更具有代表性[12]。Delage P,et al.对Champlain 黏土开展压汞试验,定量分析孔径分布随固结压力的变化,至此压汞试验已成为研究土体微观结构的重要手段[13]。孙秀丽等利用扫描电镜(SEM)和分形几何理论对疏浚淤泥固化土的孔隙结构进行了定量研究,确定了分形维数与微观结构参数、宏观力学性质以及固化材料比例之间的关系[14]。刘风华等采用CT 技术研究了渠道边坡膨胀土的微观结构,从分形几何角度研究其内部裂隙规则度,发现膨胀土内部裂隙具有明显的不规则性[15]。杨明辉等引入分形理论,对非饱和土的孔隙及通道分布的非均质性及瓶颈效应进行了模拟,探讨了非饱和土吸湿与脱湿过程中的土水特征曲线的滞后效应以及渗透规律[16]。陶高梁等通过压汞试验对武汉黏性土的孔隙特征进行研究,发现不同干密度土样均存在临界孔径现象,且临界孔径前后孔隙分布规律有显著区别[17]。陈毅等采用压汞法(MIP)和扫描电镜法(SEM)分别对定西市遗址土内外部土样的微观孔隙结构进行研究并引入分形理论对其孔隙特征进行评价,研究表明随着风化时间的增长,外部土体的孔隙总体积和表面分形维数逐渐减小[18]。
上述研究成果证明分形理论能较好地描述土体孔隙结构的复杂性和不规则性,但前人的研究主要集中于采用单一的分形模型来描述土体孔隙结构,并且忽略了不同分形模型对不同土体的适用性问题。此外,前人所采用的分形模型均假设孔隙是光滑的圆柱体,无法准确地描述土体真实的孔隙结构特征。因此本文以广饶县农田盐碱土为研究对象,压汞试验为技术手段,探索不同深度盐碱土孔隙的迂曲程度,并根据分形几何学理论优选出体积分形模型。研究结果可提高对该地区盐碱土微观孔隙特征的认识,为揭示盐碱土的渗透性和盐碱地修复提供参考。
1 材料与方法
2.1 试验材料
试验土样取自山东省东营市广饶县美奥生物有限公司(37°18′7″N,118°38′7″E)附近,如图1 所示。在取样过程中,采用环刀法取样以保证试验土样的原始结构不被破坏。试验取样深度范围为0~60 cm,分别取深度为0、10、20、30、40、50 和60 cm 处的均质土样作为微观结构分析的样品。
1.2 试验方法及原理
根据《土工试验规程》规定,采用变水头试验测试不同深度土壤的渗透系数。取不同深度的土样,将其制成5 mm×5 mm×10 mm 的长方体,试验采用真空冷冻干燥法(如图2a 所示)除去土样中的水分;并采用美国康塔仪器公司生产的全自动压汞仪PM-33-18 进行压汞试验(如图2b 所示)。
压汞法是在一定压力下将汞压入到介质中,根据压力和压入汞的体积换算出各类孔隙的大小,压汞法是分析土体微观结构最通用的方法。压汞法的原理是非浸润性液体在没有压力时不会流入固体孔隙,圆柱形孔隙注入液体所需压力大小根据Washburn 公式计算[19]:
式中:P为施加压力,Pa;σ为浸入液体的表面张力系数,N/m;θ为导入液体与固体材料的接触角,°;r为圆柱形孔隙半径,m。
根据相关的文献[20],取σ=0.485 N/m,θ=140°。从压汞结果中可以得到压力与进汞体积之间的关系,利用公式(1),通过压力P求得对应的当量直径d,以此转换得到土的孔隙分布和表面积等孔隙特征参数。
2 盐碱土孔隙分形模型
2.1 空间填充模型
Ji X,et al.根据水泥混凝土发生水化反应填充大孔隙生成小孔隙的原理构造了空间填充模型,经过大量的试验证实,空间填充模型同样适应于土体的分形研究。空间填充模型的详细推导过程可参考文献[21],计算公式为:
V为累积孔隙体积,cm3/g;t为常数;r为孔隙半径,m;DK为基于空间填充模型的分形维数。
根据压汞试验测定的累积孔隙体积V与孔隙半径r分别取对数后得到的直线斜率,即可求得分形维数DK。
2.2 Menger 海绵模型
Menger 海绵模型是研究固体材料分形维数最常用的模型之一,其具体的推导过程可参考文献[22],计算公式为:
V为累积孔隙体积,cm3/g;k为比例常数;DL为基于Menger 海绵模型的分形维数;P为进汞压力,MPa。
根据压汞试验的结果,以log(dV/dP)为纵坐标,以logP为横坐标,求得拟合直线的斜率,即可求得分形维数DL。
2.3 毛细管压力曲线法模型
根据毛细压力对数与湿润相饱和度对数的线性关系可求得孔隙的分形维数,其具体的推导过程可参考文献[23],计算公式为:
S为孔径小于r的累积孔隙体积百分比,%;DM为基于毛细管压力曲线法的分形维数;Pmin为最大孔径对应的毛管压力,MPa;P为孔径为r所对应的压力,MPa。
根据压汞试验结果,以logS为纵坐标,以lgP为横坐标,对不同深度盐碱土压汞试验中进汞过程中的数据进行线性拟合,求得拟合直线的斜率,即可求得分形维数DM。
2.4 热力学模型
热力学模型是由张玉良等人推导得出的,其具体的推导过程可参考文献[24],计算公式为:
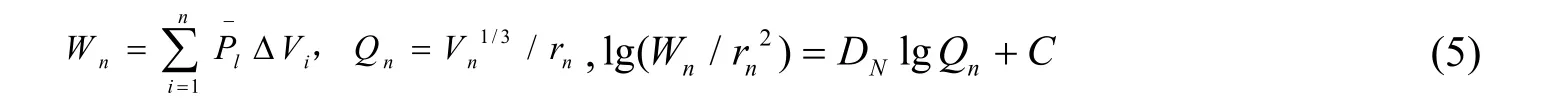
Pl为第i次进汞的平均压力,MPa;ΔVi为第i次进汞增量,cm3/g;n为施加压力的间隔次数;rn为第n次进汞时对应的孔隙半径,nm;DN为基于热力学模型的分形维数。
根据压汞试验结果,以lg()为纵坐标,以lgQn为横坐标,对不同深度盐碱土压汞试验中进汞过程中的数据进行线性拟合,求得拟合直线的斜率,即可求得分形维数DN。
2.5 孔轴线模型
孔轴线模型是由尹红宇以Von koch 曲线模型为基础所提出的,具体的推导过程可参考文献[25],计算公式为:
V为累积孔隙体积,cm3/g;DT为基于孔轴线模型的分形维数;r为孔隙半径,nm。
根据压汞试验结果,以lg(d2V/dr2)为纵坐标,以lgr为横坐标,对不同深度盐碱土压汞试验中进汞过程中的数据进行线性拟合,求得拟合直线的斜率,即可求得分形维数DT。
3 结果与分析
3.1 基于不同分形模型的分形维数计算
利用上述5 种分形模型计算公式处理不同深度盐碱土的压汞数据,并计算其分形维数。图3 为不同分形模型所计算的40 cm 深度处盐碱土孔隙的分形维数,其它深度盐碱土孔隙的分形维数计算结果见表1。由分形几何学理论可知,多孔介质的孔隙结构分形维数的合理范围为2~3,分形维数反映研究对象的复杂程度,分形维数越大,说明研究对象复杂程度越高。
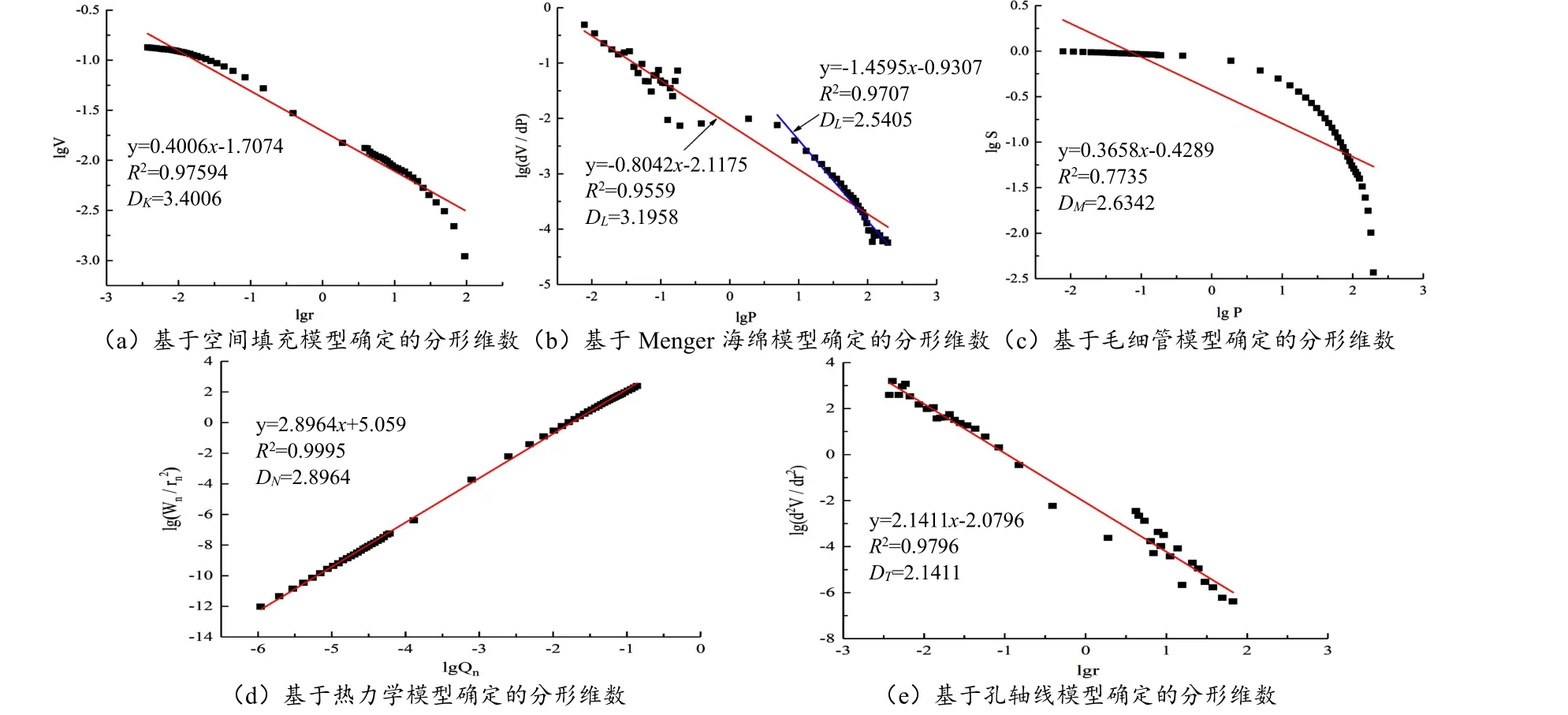
图3 40 cm 深度处土样的分形维数计算Fig.3 Fractal dimension calculation of soil sample at 40 cm depth
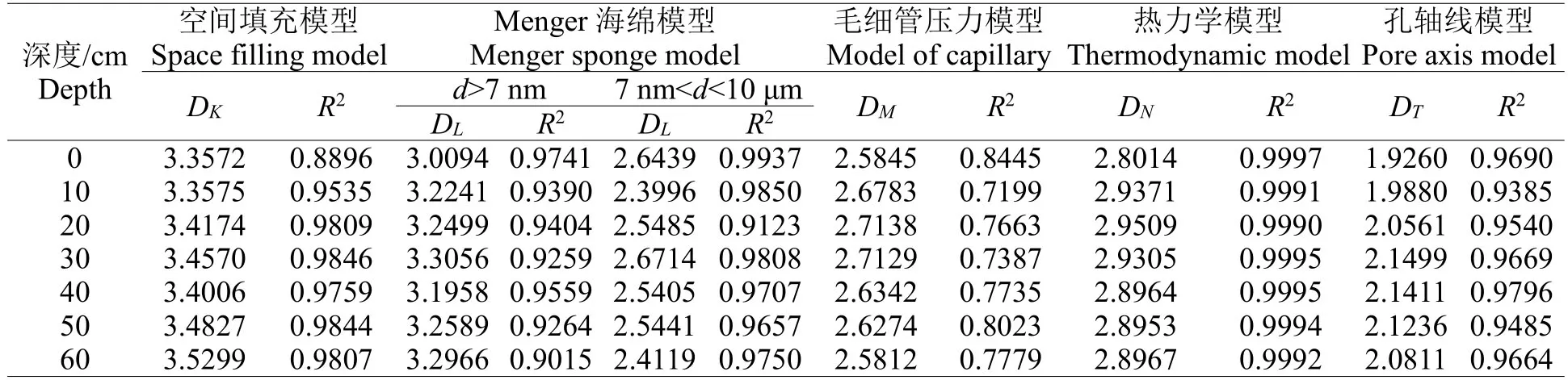
表1 不同深度土样的分形维数计算结果Table 1 Calculation results of fractal dimension of soil samples with different depths
3.2 基于孔轴线分形模型的孔隙结构特征分析
孔轴线模型是在Von koch 孔隙模型的基础上所提出来的,它被用来描述孔隙弯曲的复杂程度,因此由此模型所得分形维数的取值大于0 即可,并且分形维数越大,代表孔隙的弯曲程度越复杂,孔隙曲率越大,渗透系数越低。由图3(e)和表1 可知,lg(d2V/dr2)与lgr呈较好的线性相关,线性相关系数在0.9385~0.9796 之间。不同深度盐碱土孔隙结构拟合所得的分形维数DT在1.9260~2.1499 之间变化,且随深度的增加,孔轴线模型确定的分形维数呈现先增加后减小的趋势。由此可见,该研究区域内盐碱土孔隙弯曲程度较大,这也是其渗透性差的原因之一。
孔轴线模型所确定的分形维数与土壤渗透系数的关系如图4 所示。由图4 可以看出,孔轴线模型所确定的分形维数与土壤渗透系数之间表现出良好的负相关性,这说明随着孔轴线迂曲程度增加,土壤渗透系数逐渐减小。农田盐碱土的渗透系数在4.35~10.15 mm/h 之间,这说明农田盐碱土的渗透能力较低,这为盐碱地的治理带来了较大的阻力。
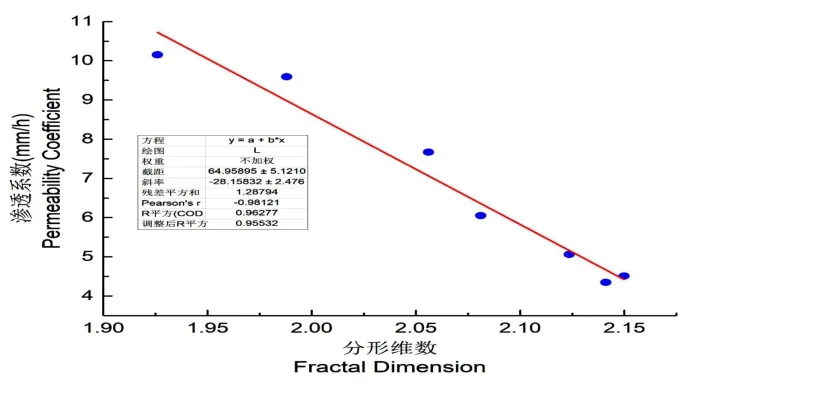
图4 土壤渗透系数与分形维数DT 的关系Fig.4 Relationship between soil permeability coefficient and fractal dimension DT
3.3 基于体积分形模型的孔隙结构特征分析
空间填充模型确定不同深度盐碱土的分形维数时,lgr与lgV呈较好的线性相关,线性相关系数在0.8896~0.9846 之间,但分形维数DK均大于3,这说明黄河三角洲盐碱土孔隙结构相当复杂且无序,已经超出欧氏三维空间理论范畴,仅能用分形维数来进行阐明。根据经典几何观点可知其明显偏离了分形维数的合理定义,因此空间填充模型不能定量表征盐碱土孔隙结构的复杂程度。
Menger 海绵模型确定不同深度盐碱土的分形维数时,lg(dV/dP)与lgP呈线性相关,线性相关系数较高,但由其确定的分形维数均大于3(如表1 所示),因此Menger 海绵模型不能在整体孔径尺度范围内定量表征盐碱土孔隙结构的复杂程度。孔隙的孔径在7 nm~10 μm 区间时,Menger 海绵模型所确定的分形维数DL在2.3996~2.6714 之间且线性相关系数在0.9 以上。由此可以看出,Menger海绵模型仅能较好表征盐碱土孔径在7 nm~10 μm 区间内的孔隙分形特征。
毛细管压力法模型确定不同深度盐碱土的分形维数时,lgS与lgP分阶段线性相关,这表明在不同孔隙直径区间范围内盐碱土孔隙具有不同的自相似度。从整体孔径尺度范围来看,不同深度盐碱土孔隙的分形维数DM在2.5812~2.7138 之间,线性相关系数在0.8 左右。尽管lgS与lgP的线性相关系数较低,但分形维数在合理范围内,因此采用毛细管压力法模型确定的分形维数在一定程度上仍可定量表征盐碱土孔隙结构的复杂程度。
以上4 种体积分形模型中,空间填充模型所确定的分形维数不能有效表征孔隙的分形特征;Menger 海绵模型仅能定量表征孔径在7 nm~10 μm 区间内的孔隙分形特征;在使用毛细管压力法模型确定分形维数时,没有充分考虑实际进汞过程中间隔施加压力所得到的数据点不够密集的情况,导致在整体孔径尺度范围内线性相关性较低;热力学模型所确定的分形维数在整体孔径尺度范围内均能有效地定量表征盐碱土孔隙的分形特征,且与lgQn的线性相关系数较高。综上所述,在评价该区域盐碱土孔隙结构的复杂程度时,应用热力学模型的效果是最好的。
4 结论
(1)孔轴线模型所得的盐碱土孔隙结构的分形维数在1.9260~2.1499 之间,且随深度的增加,其分形维数呈先增加后减少的趋势。0~30 cm 范围内,孔隙的迂曲程度逐渐变大,30~60 cm 范围内,孔隙的迂曲程度逐渐降低。盐碱土的渗透系数在4.35~10.15 mm/h 之间,孔轴线模型所确定的分形维数与土壤渗透系数之间呈现较好的负相关性。
(2)采用4 种体积分形模型计算孔隙体积分形维数,空间填充模型不能应用于定量表征盐碱土孔隙的分形特征;毛细管压力法模型在不同孔径尺度范围内存在不同的分形维数,但在整体孔径尺度范围内所体现出的分形维数在一定程度上也能定量表征孔隙的分形特征;当孔径在7 nm~10 μm 区间内时,Menger 海绵模型能定量表征盐碱土孔隙的分形特征,而当孔径d>10 μm 时,Menger 海绵模型无法得到合理的分形维数;热力学模型所确定的分形维数在整体孔径尺度范围内能有效表征孔隙的分形特征。通过比较4 种体积分形维数可知,热力学模型能较好地定量表征该区域盐碱土孔隙结构的分形特征。

