跨活动断裂带城市浅埋地铁隧道结构两阶段设计方法研究

安韶，陶连金，边金2，张宇，韩学川

(1.北京工业大学工程抗震与结构诊治北京市重点实验室，北京，100124；2.广东海洋大学海洋工程学院，广东湛江，524008)

目前，我国很多城市正在进行大规模地铁建设。但北京、乌鲁木齐、天津及太原等城市位于高烈度区且存在多条活动断裂带，由于地铁工程走向往往取决于城市交通功能的需求，避让原则[1]常常无法实现。汶川地震震害经验表明，跨活动断裂带的地下隧道结构在断层错动与地震动的共同作用下破坏非常严重，且断层错动是引起结构破坏的主要因素[2-4]。跨断层隧道结构的影响研究方法包括震后调查、模型试验及数值模拟，其中震后调查受诸多条件限制，难以大规模开展，因此，后2 种方法在近年内得到广泛应用。KONTOGIANNI等[5]通过模型试验研究了不同断层倾角的逆断层、走滑断层作用下隧道衬砌管片环向接头部位应力应变规律。LIN 等[6]通过提升底板试验模拟了逆冲断层作用下砂土中盾构隧道变形破坏特点。ZHAO 等[7]通过模型试验提出了一种新型柔性接头材料，并通过数值模拟验证了断层错动作用下该柔性接头的减灾效果。CAI 等[8]结合模型试验和数值模拟2种方法研究了隧道的变形与应变，分析了模型边界及隧道埋深对隧道结构的影响规律。刘学增等[9-10]通过模型试验研究了错动作用下山岭隧道结构的基岩剪切带分布、应变分布规律及结构破坏形态，之后又分析了铰接式隧道的抗错断效果。孙风伯等[11]推导了隧道最大节段长度并通过实验验证。王明年等[12]展开了断裂黏滑错动作用下模型试验并研究了减震缝与减震层的减震效果，为实际隧道工程的建设提供了参考依据。在数值模拟方面，SHAHIDI 等[13]针对伊朗Koohrang-III 输水隧道跨活动断裂的情况，提出断层带部分衬砌采用铰接设计方法，并计算确定了适宜的衬砌节段长度和柔性连接宽度。张维庆[14]采用数值模拟方法研究了穿越断层隧道在断层错动和地震力分别作用下的震害机理。赵颖等[15]采用数值模拟方法研究了走滑断层位错作用下城市地铁隧道衬砌结构的损伤发展，重点分析了结构损伤的开始部位、发展过程以及最终的损伤程度,并建立了能够估计结构损伤范围及破坏最严重位置的统计关系式。赵坤等[16]采用有限元法通过正交试验研究了衬砌节段长度、柔性连接宽度、柔性连接材料强度对衬砌结构内力的影响。以上成果对于穿越活动断裂带的地下隧道工程具有一定的指导意义，但在进行断层错动作用的隧道响应分析时，断层错动位移的计算均以给定地震条件下的断层破裂长度统计结果为基础，本质上属于确定性方法[17]，难以反映断层错动的随机性影响，在形式上也难以与基于概率论的地震动危险性相协调。因此，为了考虑断层错动发生的随机性和参数的不确定性，KIREMIDJIAN[18]提出了基于概率的断层错动危险性分析方法，王丽萍等[19]采用该方法计算了乌鲁木齐地铁区间隧道在不同超越概率条件下的设防错动位移。在概率分析方法的基础上，两阶段设计方法在抗震设计中得到广泛应用。两阶段设计方法是通过总结人类历史上历次地震的经验教训，考虑国民经济发展水平和工程实践，采纳最新的科学研究成果而制定，其第一阶段进行结构的弹性验算，第二阶段进行结构的弹塑性验算。但是，目前两阶段设计方法在断层错动设计分析中的研究和应用较少，因此，借鉴建筑抗震设计方法，探究一种适用于断层错动的两阶段设计方法具有重要的意义。本文作者结合乌鲁木齐轨道交通2号线工程某区间隧道工程，首先借鉴抗震设计中的“两阶段三水准”设计方法，给出断层错动作用下两阶段设计内容；其次基于包络设计原则，通过建立三维弹塑性有限元模型对比分析隧道二次衬砌的塑性应变、剪应变及拉压损伤因子等参数，确定最不利错动面的位置。最后基于两阶段设计原则，分析最不利工况下不同设计阶段采用柔性接头减灾方法的减灾效果。

1 工程概述

乌鲁木齐轨道交通2号线某区间隧道穿越西山断层北支，该分支断裂很复杂，断层破碎带主要由煤层组成，为Ⅴ级围岩，地层结构极其破碎，稳定性差。拟建区间底板埋深为17.6～26.5 m，标高为831.0～842.6 m，地质剖面简图见图1。西山断层形成于中更新世中晚期，最新活动时间为晚更新世晚期，属晚更新世活动断层，走向为N45°—75°E，倾向N，倾角为44°～83°，具逆冲性质。穿越断层段前后200 m 范围内隧道区间拟采用矿山法施工，其余地段拟采用盾构法施工。依据乌鲁木齐轨道交通2号线详勘报告，为了在断层错动分析中考虑地震发生的随机性和参数的不确定性，采用错动危险性分析方法计算得到100 a内不同超越概率的竖向位移，见表1[19]。

图1 地质剖面简图Fig.1 Sketch map of geological profile

表1 不同超越概率的错动量Table1 Fault displacement with different exceeding probability

2 模型建立及参数选取

通过多次试算直至沿轴向隧道结构几乎不受断层错动的影响为止，取断层破碎带前后各100 m范围内建立三维计算模型，模型长×宽×高为252 m×68 m×60 m，隧道埋深为12 m，断层倾角为45°，隧道直径为6.7 m，模型网格划分见图2，隧道结构采用复合式衬砌。土体假设为理想弹塑性材料，采用摩尔库仑屈服准则，各土层参数见表2，衬砌结构采用ABAQUS中的塑性损伤模型，依据混凝土结构设计规范(GB 50010—2010)的规定，定义衬砌混凝土弹塑性应力应变关系。初期支护厚为0.35 m，混凝土强度等级为C45，损伤参数见表3；二次衬砌厚为0.25 m，混凝土强度等级为C50，损伤参数见表4。考虑隧道与土体之间的摩擦，其接触面设置罚摩擦，摩擦因数取为0.4。模拟分析分为3步：初始地应力平衡—隧道开挖—施加断层位移。在前2个分析步中，模型底部及侧边界施加法向约束，上部边界为自由边界；在最后1个分析步中，由于逆断层错动为上盘相对下盘作向上运动，因此，为实现逆断层错动过程，释放上盘底部及侧边界法向约束，并对整个上盘施加位移荷载以模拟断层错动。

图2 土层-隧道模型网格Fig.2 Meshing of soil-tunnel model

3 位移加载边界条件

包络设计法是对工程可能出现的情况分别计算，取最不利值进行设计。断层错动通常出现在破碎带内，但其出现的具体位置很难预测。考虑到本工程项目破碎带较宽及底部围岩性质沿纵向变化的特点，分别假定错动面发生在上盘与破碎带交界面、破碎带中点、破碎带与下盘交界面这3个位置，对同位移错动作用下的隧道结构二次衬砌损伤进行分析，以确定最不利错动面作为后续两阶段设计的基础。逆断层错动过程中，位移荷载施加在整个上盘，3种不同位置错动面的加载示意图见图3。

表2 土层物理力学参数Table2 Physical and mechanical parameters of soil layers

表3 混凝土损伤参数(C45)Table3 Damage parameters of concrete(C45)

表4 混凝土损伤参数(C50)Table4 Damage parameters of concrete(C50)

4 两阶段设计方法

图3 不同错动面加载位置示意图Fig.3 Schematic diagrams of different locations of fault rupture plane

我国建筑抗震设计思想为“安全经济”，即建筑物抗震设防后，结构和构件能充分发挥自身的承载和变形能力，减轻结构破坏，避免人员伤亡，减少经济损失。为使工程结构“安全、经济”，需要采用三水准设防目标和两阶段设计。

GBJ 11—89“建筑抗震设计规范”明确提出三水准设防目标，见表5。

三水准设防目标需采用两阶段设计实现。两阶段的设计内容见GBJ 11—89“建筑抗震设计规范”、GB 50011—2001“建筑抗震设计规范”及GB 50011—2010“建筑抗震设计规范”。随着时间的推进及人们对地震的认识逐渐加深，抗震规范内计算内容逐步细化，但各阶段的设防目标和结构在不同阶段的受力状态始终是统一的，见表6。

总结以上抗震设计规范可知，在地震作用下，第一阶段结构应处于弹性状态或部分处于弹塑性状态，第二阶段结构处于弹塑性状态，但应防止结构的整体倒塌。参考以上抗震设计内容，在采用两阶段设计方法进行断层错动分析时，设防内容保持与抗震内容一致，其基本设计内容见表7。由表7可知：在进行100 a 内超越概率为10%的错动量分析时，应保证结构处于弹性状态或部分处于弹塑性状态；在进行100 a内超越概率为3%～2%的错动量分析时，应保证结构的破坏控制在局部区域内，防止整体倒塌。依据表1所示不同超越概率的错动量，建议采用100 a内超越概率10%的错动量0.165 m作为该段区间第一阶段竖向设防位移进行设计，按照100 a 内超越概率3%的错动量0.650 m 作为第二阶段整体坍塌极限验算。两阶段设计流程见图4。

表5 三水准设防目标解析Table5 Analysis of three-level fortification target

表6 两阶段抗震设计内容Table6 Content of two-level seismic design

表7 两阶段抗断设计内容Table7 Content of two-level anti-fault dislocation design

图4 两阶段设计流程图Fig.4 Flow chart of two-stage design

5 结果分析

5.1 纵向内力分布

通过数值模拟、理论解析及实验验证等方法[13,20]，在断层错动作用下，隧道结构在断层错动面处承受的相对位移最大，沿两侧逐渐减小，沿隧道轴向各横截面内力分布规律如下。

1)弯矩沿隧道轴向呈反对称分布，在断层错动面两侧一定范围内变化剧烈，向两端逐渐减小。

2)剪力在错动面处达到最大，向两端逐渐减小。

3)轴力在错动面处达到最大，向两端逐渐减小。

因此，在进行数值模拟分析时，可先提取隧道结构沿纵向的内力分布图以初步验证模型的正确性。施加100 a 内超越概率10%断层错动位移0.165 m，以错动面1 为例，得到隧道二次衬砌沿纵向的内力分布见图5。由图5可知：施加断层错动位移以后，沿纵向隧道结构二次衬砌内力分布符合相关内力分布规律。

5.2 最不利错动面

5.2.1 变形分析

定义模型上盘边界处为0点，往右侧指向下盘方向为正，断层错动面1～3 分别发生在纵向坐标100，126和152 m处，图6所示为二次衬砌竖向位移沿隧道纵向距离的分布曲线。由图6可知：断层错动发生后，隧道衬砌沿着纵向发生了“S”状弯曲；上盘内隧道受竖向位移的作用，二次衬砌产生向上的位移0.165 m，沿隧道纵向指向下盘逐渐减小。产生这种现象的原因是模型断层下盘固定，对整个上盘施加强制位移，因此，造成错动面处相对位移最大，沿隧道轴向两侧逐渐减小，隧道在强制位移的作用下变为“S”形。

定义沿隧道纵向每延米竖向位移变化为隧道纵向转角，其计算示意图见图7。图7中，点A和B为隧道初始位置，AB长为L。施加位移荷载以后，点A'和B'为隧道变形后的位置，其中AA'竖向位移为u1，BB'竖向位移为u2，则定义的隧道纵向转角θ为

图5 二次衬砌纵向内力分布Fig.5 Longitudinal distribution of internal force of secondary lining

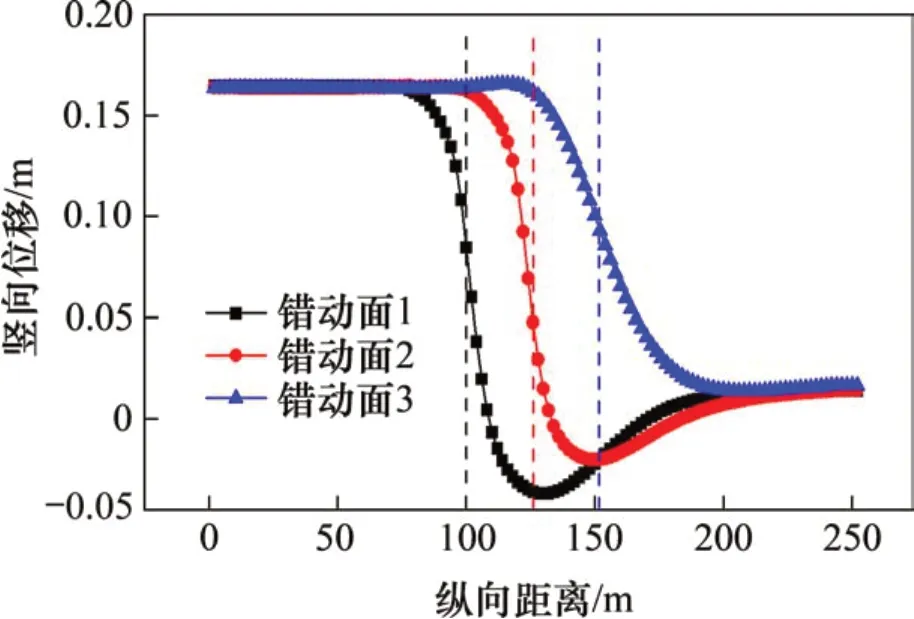
图6 竖向位移纵向分布曲线Fig.6 Longitudinal distribution curves of vertical displacement of secondary lining

图7 转角示意图Fig.7 Schematic diagram of angle

图8所示为隧道二次衬砌转角纵向分布曲线。从错动面1 到3，隧道纵向最大转角分别为0.012 18，0.011 66 及0.003 74 rad，逐渐减小，变形趋于平缓。

图8 转角纵向分布曲线图Fig.8 Longitudinal distribution curve of angle of secondary lining

5.2.2 损伤破坏分析

表8所示为不同错动面的塑性应变、剪应变、拉伸损伤因子及压缩损伤因子的分布云图，图9所示为不同错动面的各损伤指标最大值对比。由表8和图9可知：从断层错动面1 到错动面3，隧道二次衬砌各指标最大值均逐渐减小，代表结构受损越轻。产生这种现象的原因是错动面1发生在泥岩与煤层交界面处，错动面2发生在煤层与煤层交界面处，错动面3 发生在煤层与粉质黏土交界面处，其中泥岩与煤层为Ⅴ级围岩，粉质黏土为Ⅵ级围岩。从错动面1到错动面3隧道底部围岩渐软，隧道变形趋于平缓(图8)，受到的损伤也逐渐减小。因此，错动面1为最不利错动面。

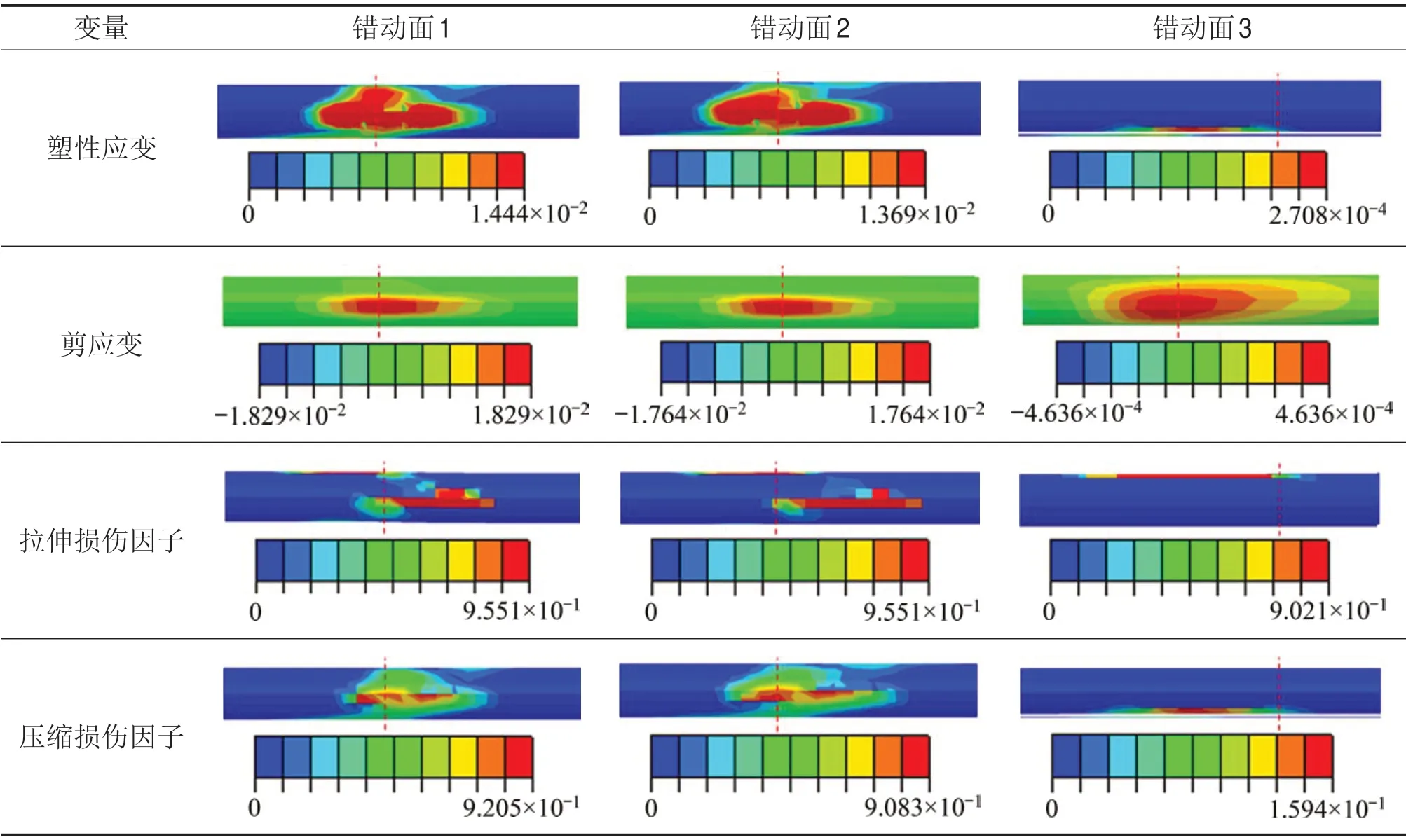
表8 不同位置错动面损伤指标分布云图Table8 Contour of damage index of different fault rupture planes

图9 不同错动面损伤因子最大值Fig.9 The maximum value of damage indexes of different fault rupture planes

断层错动作用下隧道结构受到拉压剪的共同作用发生严重破坏。以错动面1为例，隧道二次衬砌塑性应变集中分布在断层错动面处，且在横截面方向有贯通趋势，因此，未采用减灾措施以前，隧道衬砌可能发生严重破坏，隧道二次衬砌的拉压、剪切及裂缝分析陈述如下。

1)拉压损伤分析。提取错动面1隧道拱顶、拱腰及拱底处的拉压损伤因子见图10和图11。由图10和图11可知：最大受拉受压损伤因子均出现在断层拱腰处，上盘内拱顶处受拉，拱底处受压，在受损最为严重的拱腰处指向下盘方向的破碎带内拱顶处受压，拱底处受拉。由以上分析可知，二次衬砌拱腰处拉压破坏最为严重，拉压损伤因子沿纵向均呈“S”型分布，与衬砌变形一致。在ABAQUS中，拉伸损伤因子与压缩损伤因子大于0代表结构发生受拉或受压破坏，损伤因子越大，代表结构破坏越严重。由图10和图11可知：受拉损伤范围发生在纵向坐标83～129 m 处，共46 m；受压损伤范围发生在纵向坐标83～117 m 处，受压损伤范围为34 m，逆断层错动作用下，受拉损伤范围大于受压损伤范围。

图10 隧道拱顶、拱腰及拱底的受拉损伤因子纵向分布曲线Fig.10 Longitudinal distribution curve of tensile damage factor of tunnel vault,waist and invert

图11 隧道拱顶、拱腰及拱底的受压损伤因子纵向分布曲线Fig.11 Longitudinal distribution curve of compressive damage factor of tunnel vault,waist and invert

2)剪切破坏分析。由错动面1剪应变分布云图可知剪应变及最大剪应变值均分布在拱腰处。图12所示为拱腰处剪应变(绝对值)纵向分布曲线，其最大值为0.018 29。混凝土抗剪强度和抗压强度之比为0.095～0.121[21]，依据ZIA[22]的建议，混凝土的剪切模量为其弹性模量的40%。由此可求得二次衬砌(C50)允许的极限剪切应变：

式中：τ为混凝土极限抗剪强度；G为混凝土剪切模量。

由式(2)可知：混凝土极限剪切应变范围为2.210×10-4～2.841×10-4，拱腰处剪应变为1.829×10-2，远大于极限剪切应变，表示混凝土极可能发生严重的剪切破坏。

图12 拱腰处剪应变纵向分布曲线Fig.12 Longitudinal distribution curve of shear strain of tunnel waist

3)裂缝分析。CHEN等[23]提出了一种通过拉伸损伤因子dt合理计算混凝土裂缝wt的计算公式：

式中：hc为特征值长度，对于八节点积分单元而言，其等于单元边长[24]；σt为拉应力；E0为初始弹性模量。

由式(3)得到当混凝土裂缝宽度为0.2 mm 时，受拉损伤因子为0.838。

依据《水工混凝土结构设计规范》，表9给出了混凝土裂缝宽度和受拉损伤因子定义的二次衬砌(C50)开裂受损程度划分依据。

错动面1 隧道衬砌受拉损伤因子最大值为0.955 1，大于0.838，代表混凝土裂缝宽度大于0.2 mm。结合表8中错动面1 受拉损伤云图可知，最大受拉损伤因子主要分布在断层错动面及其附近，因此，该处混凝土二次衬砌裂缝发生严重的拉裂破坏。

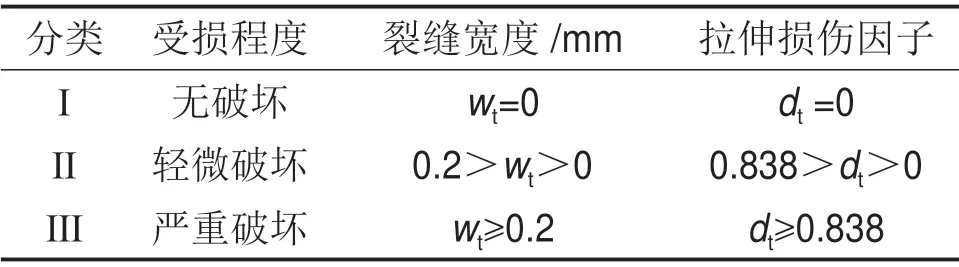
表9 二次衬砌受损程度划分Table9 Classification of damage degree of secondary lining

5.3 减灾措施

GB 50909—2014“城市轨道交通结构抗震设计规范”10.1.3节明确规定“进行隧道选线与地下车站选址时应绕避不良地质地段及地层，当无法避开时，应采取可靠的处理措施”。目前常用的抗断减灾设计方法主要包括超挖设计，铰接设计(柔性接头)及设置减震层等[25-27]，该工程采用设置柔性接头的方法。为确定衬砌节段长度，在基本设防错动位移作用下，二次衬砌的弯矩纵向分布见图5(a)，在错动面两侧32 m 处隧道二次衬砌形成反弯点，依据SHAHIDI 等[13]的研究，衬砌节段长度最大不应大于32 m，考虑到混凝土台车的宽度为6～12 m，同时考虑到防水要求，衬砌节段长度不宜设置太短，因此，节段衬砌长度最终确定为12 m，设置范围分布在断层破碎带及其附近共96 m，柔性接头长度取为1 m。按不利工况(错动面1)考虑，假定断层错动的位置发生在节段衬砌中点处，参考乌鲁木齐地铁1 号线柔性接头材料[28]，模拟中柔性接头被简化为理想弹性材料，密度为1 000 kg/m3，弹性模量为7.8 MPa，泊松比为0.47，柔性接头设置示意图见图13。

图13 柔性接头示意图Fig.13 Sketch map of flexible joints

5.4 两阶段设计分析

5.4.1 第一阶段塑性损伤分析

图14所示为塑性应变(PEEQ)、剪应变(LE23)、拉伸损伤因子(DAMAGET)及压缩损伤因子(DAMAGEC)的分布云图，与表8中错动面1 各损伤指标对比，采用柔性接头以后各损伤指标最大值及分布范围均显著减小，其中，塑性应变为7.423×10-6，降低了99.95%；剪应变为2.080×10-4，降低了98.86%，且小于允许的极限剪切应变2.210×10-4；拉伸损伤因子最大值为0.378 8，降低了60.34%，小于0.838 0。压缩损伤因子最大值为0.004 37 接近于0，降低了99.5%，塑性损伤均分布在变形缝附近局部区域内。由以上分析可知隧道二次衬砌仅在变形缝处有可能产生轻微的拉裂破坏，隧道结构整体处于弹性状态或部分处于弹塑性状态，满足第一阶段设防水准的要求。

5.4.2 第二阶段塑性损伤分析

图15所示为有无柔性接头的隧道二次衬砌塑性应变分布云图，图16所示为设置柔性接头以后的剪应变、拉伸损伤因子及压缩损伤因子分布云图。由图15可知：设置柔性接头以后，塑性应变为1.496×10-2，降低了71.91%；塑性应变分布在变形缝附近，且尚未形成贯通。由图16可知：二次衬砌剪应变为5.893×10-3，大于极限剪应变2.841×10-4，拉伸损伤因子最大值为0.954 6，压缩损伤因子最大值为0.920 5，各损伤指标均分布变形缝附近。由以上损伤分析可知设置柔性接头以后在第二阶段错动量65 cm工况下，二次衬砌依然可能发生拉压及剪切破坏，但塑性损伤范围明显降低且集中在跨断层错动面处节段隧道变形缝附近，使隧道二次衬砌的破坏发生在局部区域之内，有效防止了衬砌结构的全面倒塌，满足第二阶段设防水准要求。

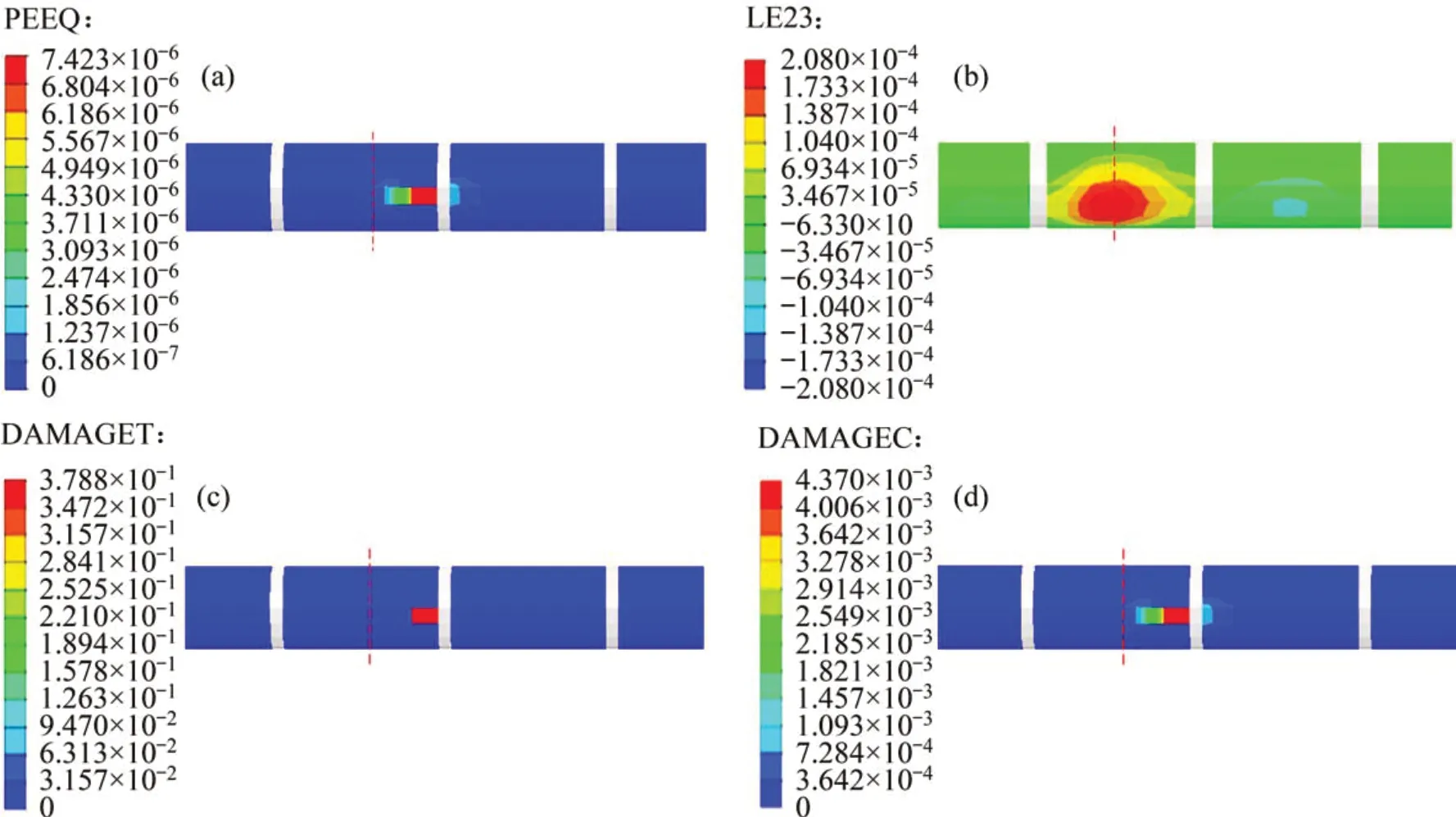
图14 塑性损伤分布云图Fig.14 Distribution contour of plastic damage

图15 有无柔性接头塑性应变分布云图Fig.15 Distribution contour of plastic strain with and without flexible joint

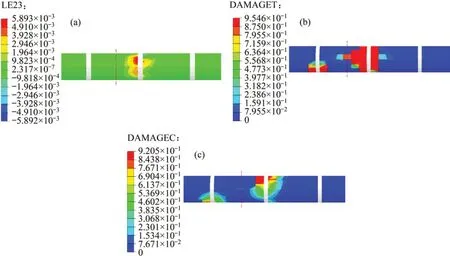
图16 塑性损伤分布云图Fig.16 Distribution contours of damage indexes

6 结论

1)借鉴抗震设计规范，考虑到断层错动的不确定性，明确了断层错动作用下两阶段设计内容，两阶段设防水准与抗震设防水准保持一致，即在进行100 a内超越概率为10%的错动量分析时，应保证结构处于弹性状态或部分处于弹塑性状态；在进行100 a 内超越概率为3%～2%的错动量分析时，应保证结构的破坏控制在局部区域内，防止整体倒塌。基于隧道混凝土结构塑性损伤模型，通过对比有无减灾措施的拉压损伤、剪应变、裂缝及塑性区分布等各损伤指标，可对是否满足以上两阶段设计设防水准要求进行初步判断。两阶段设计方法基本步骤为：整体式隧道损伤破坏分析—减灾措施—第一阶段塑性损伤分析—第二阶段塑性损伤分析。

2)错动面1发生在泥岩与煤层交界面处，错动面2发生在煤层与煤层交界面处，错动面3发生在煤层与粉质黏土交界面处。从错动面1到错动面3，错动面两侧围岩性质渐软，隧道变形趋于平缓，隧道二次衬砌损伤逐渐减小，因此，错动面1为最不利错动面。

3)乌鲁木齐地铁2号线隧道结构设置柔性接头以后，提出适用于断层错动作用下城市浅埋地铁隧道结构的两阶段设计方法。第一阶段对100 a 内超越概率为10%的0.165 m 的错动量损伤进行分析，发现隧道二次衬砌在变形缝附近有可能发生轻微的拉裂破坏，满足第一阶段设防水准要求；第二阶段对100 a内超越概率为3%的0.650 m错动量损伤进行分析，发现隧道二次衬砌虽然依然可能发生拉压及剪切的共同破坏，但设置柔性接头以后，损伤破坏主要集中在变形缝处，且二次衬砌塑性区尚未形成贯通，有效防止了结构的全面倒塌，满足第二阶段设防水准要求。