直升机低空运行飞行数据模拟
徐于松,葛红娟,薛建良,倪优扬
(南京航空航天大学民航学院,南京 211106)
近年来,随着中国通用航空业的快速发展,通用航空事故量也在增加,2010—2017年共发生通用航空事故96 起。为保障持续适航,提高直升机运行安全,需进行直升机安全监控与预警技术研究。直升机安全监控与预警技术研究的核心是通过运行数据分析超限事件的数据特征。然而,目前直升机安全监控制度尚未建立,缺乏可靠的运行数据来源,安全监控技术研究无法开展。因此,需要进行直升机飞行数据模拟技术研究,为直升机安全监控与预警技术研究提供数据支持。
航空器系统复杂,难以直接用数学模型描述,可使用计算机开展仿真和模拟。Xu 等[1]研究了基于飞行员—航空器—环境复杂系统仿真的适航验证方法。孟祥光等[2]和涂章杰等[3]使用仿真方法研究了极端条件下复飞和爬升梯度的符合性验证方法。高振兴等[4]研究了民机自动飞行模式下垂向通道的仿真验证方法。Purvis 等[5]使用PenSource 飞行模拟器作为航空器故障诊断和自我修复的验证平台,且该仿真技术还被用于航空发动机系统仿真验证[6]。文献[7-9]研究了航电传感器的故障诊断方法和系统仿真验证,同时,该仿真方法还被用于无人机故障注入和诊断[10]。以上研究主要用于固定翼航空器和无人机单一系统或功能仿真验证,直升机相关研究较少,且不能反映航空器在实际运行过程中的特定飞行场景。而直升机安全监控需要满足CCAR-27 和CCAR-29 部中规定的持续适航要求,如29.143 条规定的特定风环境下的直升机操纵性和机动性要求。飞行数据模拟平台需要提供各种直升机超限事件的全部运行数据,用于直升机安全监控与预警算法研究。因此,飞行数据模拟平台除了需要仿真特定风环境下的直升机动力学参数以外,还需要模拟其他重要系统的状态数据,以供直升机安全监控项目的研究。
针对目前直升机安全监控研究缺乏系统运行数据的情况,在直升机飞行仿真的基础上,增加了用于模拟极端大气风环境下飞行状态的大气风环境模型,建立了发动机关键数据和航电传感器模型,模拟发动机和航电系统的运行数据,最终建立直升机低空运行飞行数据模拟系统,以供直升机安全监控与预警算法研究。
1 系统架构
直升机安全监控数据模拟,不仅需要符合直升机实际运行状态,而且要考虑模型和系统的复杂度。因此,选择反映直升机实际运行状态的部分关键系统作为安全监控数据源,具体包括:控制系统模型、动力学模型、发动机关键数据模型、航电传感器模型和大气风环境模型。飞行数据模拟系统架构如图1所示。

图1 飞行数据模拟系统架构Fig.1 Flight data simulation system framework
其中,控制系统模型通过人机交互界面输入目标控制参数,输出直升机达到目标状态所需的实际控制量。动力学模型是整个飞行数据模拟系统的核心,其输入控制系统的控制量、大气风环境数据和发动机运行数据,输出直升机的运行状态数据;发动机关键数据模型用于模拟发动机扭矩等关键运行数据。航电传感器模型包括:大气数据传感器、组合导航系统、卫星导航(GPS)和无线电高度表等,这些航电传感器模型根据输入的直升机飞行状态数据,解算出航电系统运行数据,最终输出直升机安全监控所需的直升机运行数据。大气风环境模型用于模拟真实大气风环境下的直升机运行数据,通过向系统输入大气速度和方向实现模拟不同的大气风。
2 系统构成
2.1 动力学模型
使用小扰动线性方法建立直升机动力学模型。首先根据牛顿运动定律和牵连运动,将直升机在空中的运动分解为空间平动和绕直升机质心的定点转动。建立直升机动力学方程为
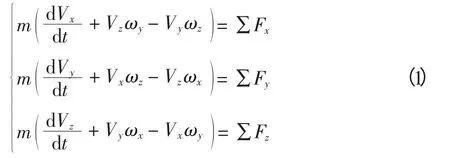
其中:m 为直升机质量;Vx,Vy,Vz为空速在机体轴x,y,z 方向上的投影;ωx,ωy,ωz为直升机在x,y,z 方向上绕机体轴转动的角速度;Fx,Fy,Fz为机体轴在x,y,z 方向上的力投影。
将各种角加速度投影到直升机3 个机体轴上,由刚体转动定律[2],可建立直升机绕三轴的力矩平衡方程式为

其中:Ix,Iy,Iz为直升机的惯量积,因为直升机对xOz 平面对称,故惯量积Ixy、Iyz等于0,因此上式中不含二者;Mx,My,Mz为三轴上的力矩。
在小扰动情况下,直升机的各运动参数可用其在基本状态下的微扰变化表示。直升机运动方程经降阶和线性化后的9 阶线性数学模型可描述为

其中:X 为飞行状态,X=[VxVyVzωxωyωzγ θ ψ]T,γ 为机体滚转角,θ 为机体俯仰角,ψ 为机体航向角;Y为模型输出量;控制向量U 为相对平衡位置的控制量,U=[δcδaδeδp]T,δc为总距,δa为横向周期变距,δe为纵向周期总距,δp为尾桨桨距。A、B 为状态系数矩阵和控制系数矩阵;C 是单位矩阵;D 为Y 对U 的系数矩阵,D=0。
由于直升机的特性参数与飞行状态密切相关,所以直升机的数学模型也不是定常状态方程,其A,B 系数矩阵随着飞行状态的变化而改变。为了避免仿真时有大量计算,可将直升机的配平状态按前飞速度分成N个系数矩阵,直升机动力学模型解算时以该飞行状态接近的系数矩阵为基准模型,可提高模型解算精度,悬停状态看作是前飞速度为0 的状态。选取具有代表性的几个常用飞行速度加以分析,分别是悬停、30 km/h、60 km/h、90 km/h、125 km/h、150 km/h。
基于直8F 直升机机重为5.8 t,重心在-0.050 5 m,垂直速度为0 时的飞行配平数据,建立直升机动力学模型,部分飞行配平数据如表1所示。

表1 直8F 飞行配平数据Tab.1 Flight data of Z-8F
2.2 大气风环境模型
大气风环境是影响直升机安全运行的重要因素。建立大气风环境模型,以模拟真实大气环境下的直升机运行数据,并实现极端大气风环境下的直升机飞行仿真。
使用数值模拟方法将大气自然风分为基本风、阵风、渐变风和噪声风4 个组成部分,最终的大气风环境可由这4 种风任意合成。
基本风速为

其中:风速量为K(m/s)。
阵风可分为梯形阵风、矩形阵风和减余弦阵风,是风切变的主要表现形式。减余弦阵风风速为

其中:Vmax为最大风速;t 为当前时间;Tr1为风起始时间;Tr为风持续时间。
渐变风速为
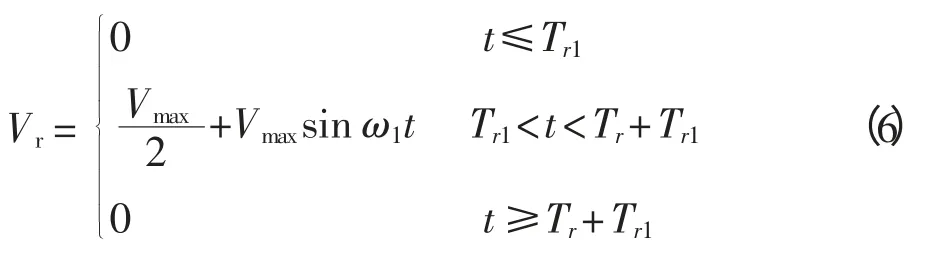
其中:ω1为变化速率。
噪声风用于模拟指定相对高度上风速变化的随机特性。其风速可表示为

其中:Sv(ωi)为第i 个随机分量的振幅;ωi为第i 个分量的角频率;Δω 为随机分量的离散间距,其取值范围为0.5~2.0 rad/s;φi为在0~2π 之间服从均匀概率分布的随机变量;m 可取50,表示50 个噪声分量的叠加。
自然风由以上4 种风重构而成,建立实际风速模型为

2.3 控制系统模型
控制模型是直升机飞行数据模拟系统中的关键模块,决定了飞行仿真的稳定性和飞行数据的有效性。控制系统通过接收手柄或界面上的输入信息,确定需要控制的目标(姿态、速度和高度等),相应的控制模型会向直升机动力学模型输出控制量(总距、纵向周期变距、横向周期变距、尾桨桨距),使飞行状态符合控制目标,保持直升机的稳定运行。
设计了3 种控制模式,包括:增稳、飞控和区域导航模式。增稳模式为手柄直接向直升机动力学模型输入控制量,包括:总距、纵向周期变距、横向周期变距和尾桨桨距;飞控模式是以航向、速度和高度等单个参数为控制目标的单通道控制模式;区域导航是以飞控模式为内回路,航线控制为主要目标的自动导航飞行模式。
具体的控制模型以航向控制为例,需要考虑转弯过程的侧偏问题。消除侧偏的协调转弯控制模型如图2所示。

图2 转弯横-航向控制Fig.2 Turning cross-heading control diagram
航向通道采用变增益PID 控制方法,当需要改变航向时,航向指令(ψd-ψ)产生滚转角指令γd,直升机通过侧向倾斜旋翼获得偏转航向所需的向心力。滚转倾斜姿态产生的航向偏转速率ωzd,需要通过尾桨机动使直升机机头与航向保持一致,同时引入ay(侧向加速度)信号以减小侧滑,从而达到协调转弯的目的。当接近航向时,滚转角逐渐恢复到平衡位置,避免滚转角复位而航向角未到所导致的机头快速改变航向及由此产生较大侧滑。
其控制律为

其中:γd为给定的滚转角;ωzd为给定的偏航角速率。
2.4 发动机关键数据模型
发动机系统是直升机安全运行的关键系统,由于发动机系统的复杂性,模型建立困难且运算复杂,难以应用到仿真中,以发动机功率、扭矩、油门和转速与直升机前飞速度的数值关系,建立发动机数值模型,以反映飞行过程中发动机的运行参数响应特征。
表2和表3为直8F 在100 m 高度,垂直速度为0,发动机在额定转速6 000 rpm 时,发动机功率和前飞速度、油门和可用功率的部分对应数据。

表2 需用功率与前飞速度关系Tab.2 Required power vs.forward speed

表3 油门与可用功率关系Tab.3 Throttle vs.available power
将表2数据绘制成数值曲线,如图3所示,可见直升机需用功率与飞行速度成马鞍形曲线,前飞速度和需用功率为非线性关系。
同时,发动机扭矩与功率需满足关系为

其中:P 为输出功率;T 为发动机扭矩;N 为转速;K 为常数。由式(10)可知,在发动机额定转速下,发动机扭矩与功率成正比,可建立发动机扭矩和功率的线性方程。

图3 直升机需用功率随飞行速度曲线Fig.3 Helicopter required power vs.flying speed
使用线性插值法在发动机额定转速的前提下建立油门—可用功率—前飞速度的数值关系,并计算对应的发动机扭矩,建立发动机数值计算模型。模拟直升机飞行时,通过油门控制直升机飞行速度的过程,达到发动机运行数据与直升机飞行状态关联的仿真目标。
2.5 航电传感器模型
直升机飞行数据模拟需要模拟多种航电传感器的运行数据。根据相应航电传感器的工作原理,建立了多种航电传感器的仿真模型,包括:大气数据传感器、组合导航系统、无线电高度表和卫星导航(GPS)等。
以三轴大气数据传感器为例,大气数据传感器的主要功能是直接测量直升机环境中的动压、静压、总温参数,并将参数传输给大气数据传感器,解算出直升机的空速、迎角和静温等关键参数。而飞行数据仿真系统是通过飞行状态参数计算大气数据传感器的运行参数,模拟大气数据计算过程。
静压为
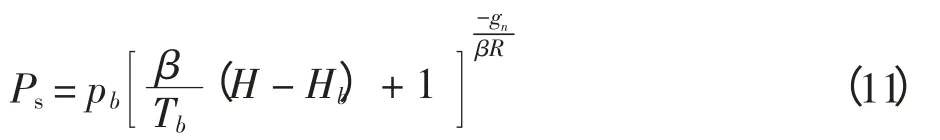
其中:pb、Tb、Hb、R、β 和gn都为常数[11],且分别等于标准大气状态下各相应层中的数值,可由直升机高度计算静压量;H 为直升机飞行高度。
马赫数方程为

其中:Vt为真空速;C 为声速;k 为空气绝热系数,k =14;ρs为对应高度的大气密度。Ts为静温,可由以下方程估算,即

其中:β 为大气垂直温度梯度。
动压为

其中:Pd为动压量。
总温为

指示空速为

其中:ρ0为海平面标准大气条件下的空气密度。
真空速为

迎角为

其中:Vtx和Vtz为真空速在机体Ox 轴和Oz 轴上的速度分量。
侧滑角为

其中:Vty为真空速在机体Oy 轴上的速度分量。
使用Matlab/Simulink 建立上述航电传感器的仿真模型。该仿真模型通过UDP 网络传输等方式实时接收仿真的飞行状态数据,得到动压、静压、总温、静温及迎角、侧滑角等航电传感器运行数据。
3 系统集成和仿真验证
使用直8F 飞行数据建立直升机动力学模型,基于MFC 和C++,在Windows 32 位系统下建立直升机飞行仿真软件,在Matlab 7.0 平台上搭建航电传感器仿真Simulink 模型,并使用UDP 方法进行数据传输,实现各个模块的功能集成。

图4 飞行仿真软件主界面Fig.4 Main interface of flight simulation software
飞行仿真软件界面如图4所示,主要分为3 个模块。界面左侧是数据实时显示模块;下方为控制模块,用于控制指令的输入;中间为各种信息的显示模块,是多个子页面的集合,其它页面还包括:位置、控制量、姿态和加速度等数据的实时曲线显示。
模拟直升机在30 km/h、60 km/h 和90 km/h 前飞速度时的稳定飞行状态,其飞行状态参数如图5所示。与表1数据对比,验证稳定前飞时直升机配平仿真数据与实际运行数据的偏差。

图5 直升机飞行状态参数Fig.5 Helicopter flight status parameter
由图5可知,直升机飞行数据模拟系统可以模拟直升机在不同速度之间转换的动态飞行过程,并保持前飞速度恒定的飞行状态。根据表1数据,比较30 km/h、60 km/h 和90 km/h 时相同的稳定前飞速度下的直升机配平数据,偏差均小于0.01°,相对误差均小于2.6%,仿真数据准确度高,可用于直升机安全监控算法研究。
直升机安全监控算法研究需模拟特定飞行场景下的直升机飞行数据,以直升机前飞状态遭遇阵风为例,验证阵风场景下飞行状态数据是否符合实际直升机飞行特点。直升机在100 m 高度,保持前飞速度36 km/h,遭遇10 m/s 风速的垂直向下的阵风。直升机在阵风情况下的动态响应曲线如图6所示。
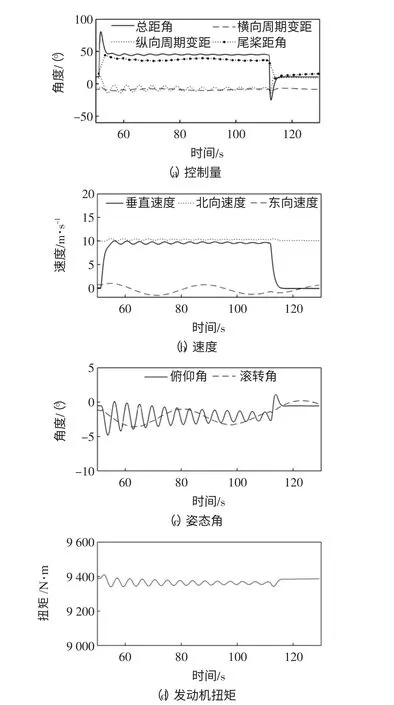
图6 直升机阵风动态响应Fig.6 Dynamic gust response of helicopter
由图6(b)可知,在52 s 时,直升机受阵风干扰垂向空速突然变为10 m/s,直升机飞行姿态受到干扰。直升机自动控制系统响应阵风干扰,控制总距、发动机扭矩等控制量,稳定直升机姿态,并保持前飞速度。稳定过程中,直升机姿态仍受到干扰,持续波动,但波动幅度逐渐减小。阵风消失后,直升机迅速回到原来的稳定飞行状态。
由此过程可知,直升机在阵风情况下的飞行仿真数据与实际直升机运行数据相符,各模块的数据响应与直升机运动过程一致,系统仿真准确度高。
直升机安全监控与预警算法研究是利用数据分析直升机运行过程是否存在安全风险。在阵风响应这一案例中,可通过调整控制系统,改变飞行员对阵风响应的操作程序,分析阵风飞行场景下不安全操作的系统运行数据特征和阈值,如最迟应在阵风发生t 时间内进行θ 角度的总距操作,否则可能发生危险。从而在实际直升机运行过程中,快速监控分析运行数据中是否发生过相应的潜在风险事件,及时采取改进措施,消除潜在安全风险。
4 结语
针对直升机安全监控研究缺乏特定飞行场景状态数据的问题,建立了直升机低空运行飞行数据模拟系统,可进行不同大气风环境下飞控、航电传感器和发动机部分数据的综合仿真。验证结果表明,该系统模拟的直升机配平数据与实际直升机运行数据相对误差小于2.6%,模型准确度高,可模拟阵风等不安全飞行场景下的系统运行数据,辅助直升机安全监控系统确定超限事件的关键运行数据和阈值特征,为快速分析和确定超限事件提供数据基础。

