热噪声试验中平板温度边界层对近壁面声压分布影响数值分析

陈雅曦，王明杰，齐江龙

（北京强度环境研究所，北京 100076）

0 引言

高超声速飞行器面临严酷的气动噪声与气动加热等复合环境问题，热、噪声、结构之间的耦合作用十分显著，因此有必要在结构设计阶段开展热噪声试验[1]。目前的热噪声试验通常使用行波管施加噪声载荷，采用石英灯加热装置进行辐射加热模拟飞行器经历的热噪声环境[2-3]。

热噪声试验中的试件表面温度常常高达八九百摄氏度，在壁面附近会形成一层薄薄的温度边界层；行波管内声波在向壁面传递时必须先通过这一温度边界层，而温度边界层密度非均匀，会使声波发生散射，导致入射方向声压的衰减。在北京强度环境研究所进行的热噪声试验研究中发现，行波管内高温壁面处测得的声压比无热辐射的常温壁面处测得的声压在高频部分有明显衰减。付文华等[4]的研究表明，声波在非均匀温度区中的传播特性主要由介质温度分布参数和声波入射角决定，当入射声波参数和非均匀介质的温度分布特性之间满足一定条件时，声波将在介质界面上发生强烈反射甚至全反射。Robins[5-6]的研究给出平面内介质密度沿传播方向变化时的解析解，得出了声波在非均匀层状介质上的透射系数与反射系数。Tarau 等[7]采用有限差分法求解一维欧拉方程组，研究了声波垂直入射非均匀温度分布区问题，探讨了利用弧光放电产生的高温空气层形成声屏障的可行性。

为了研究热噪声试验中温度边界层对近壁面声压的影响，本文提出了频域内的非均匀介质声传播方程的有限差分求解法，相比文献[7]的方法具有更高的计算效率。首先建立声波穿过温度边界层的理论模型，运用边界层积分法求解出常温气体掠过高温壁面时温度边界层内的温度分布；之后采用有限差分法对频域内的非均匀介质声传播方程进行离散，并引入固壁边界条件，通过求解差分方程得出声波垂直入射时高温平板近壁面声压分布，旨在分析平板温度边界层对近壁面声场的影响，为修正热环境影响下的噪声加载条件提供参考。

1 模型建立

在进行热噪声试验时，试件表面由于热辐射作用被加热至几百甚至上千摄氏度。而行波管中的气体可以近似为透明介质，且流速相对较快，几乎不会从热辐射中获取热量，其温度的升高主要源于对流带来的热量，故气体温度只在贴近壁面的温度边界层内发生变化，而远离壁面的气体则可近似看作常温。考虑到温度边界层厚度相对于行波管横截面尺寸是一个小量，可以将热噪声试验行波管中的气体换热问题近似为常温气体掠过高温平板的对流换热问题。

图1 所示为在北京强度环境研究所热噪声试验装置中进行的平板隔热材料热噪声试验，试件表面温度800 ℃，总声压级156 dB，行波管中气流速度约为18 m/s。

图1 平板隔热材料热噪声试验Fig.1 Thermal acoustic test for a thermal insulation flat panel

假设壁面均匀受热，平板问题可进一步简化为二维问题。为与试验状态一致，建立以下模型：平板长度l=1 m、表面温度Tw=800 ℃，气流掠过速度（主流速度）u∞=18 m/s，来流气体温度（主流温度）T∞=300 K。图2 所示为高温平板壁面附近的温度边界层，平板最左侧为坐标原点，x、y 方向定义如图所示。

图2 平板温度边界层示意Fig.2 Temperature boundary layer of a flat panel

2 温度边界层内温度分布的求解

在已知平板长度、温度以及主流速度的情况下，可采用边界层积分法得到平板温度边界层内的温度分布。对于不可压缩牛顿流体，在物性一致、无内热源、不考虑黏性耗热的条件下，二维稳态流动的冯·卡门边界层动量积分方程[8]为

式中：δ 为速度边界层厚度；τw为壁面剪切应力。

对于普朗特数Pr＞1 或≈1 的流体，对流传热边界层能量积分方程[9]为

式中：h 为对流换热系数；St 为斯坦顿数。

对于流体掠过等温平板问题，一般假定边界层内的速度分布和温度分布满足三次多项式的形式：

式中δT为温度边界层厚度。

由式(1)、式(2)可得：

另，当温度边界层和速度边界层同时从平板前缘开始形成时，

由式(4)～式(7)可以求得平板中心位置（x=0.5）处，δ=6.1 mm、δT=5.3 mm 时的边界层速度分布与温度分布，如图3 所示。

图3 近壁面速度分布与温度分布Fig.3 Near-wall velocity distribution and temperature distribution

3 非均匀介质声传播问题的有限差分法求解

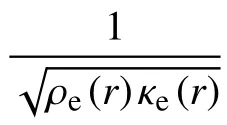
熵守恒方程为

状态方程 P=P(ρ,s)对时间求全导数有

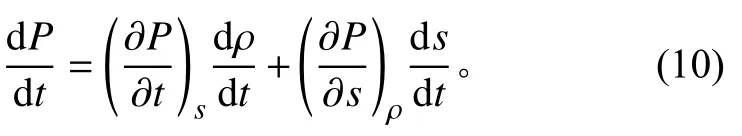
联立式(8)、式(9)并作线性化处理可得：

联立式(8)、(11)可得到非均匀介质中的声波方程[10]

通过傅里叶变换将式(12)转换为非含时方程

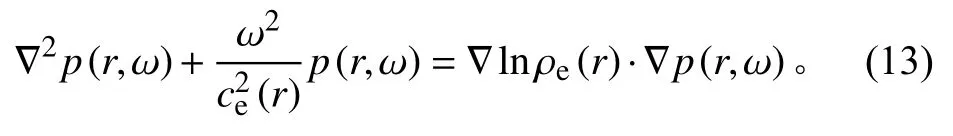
本文把穿过温度边界层的声波简化为一束垂直入射的平面波，对平板中心位置温度边界层内的声场分布进行求解，简化模型如图4 所示。

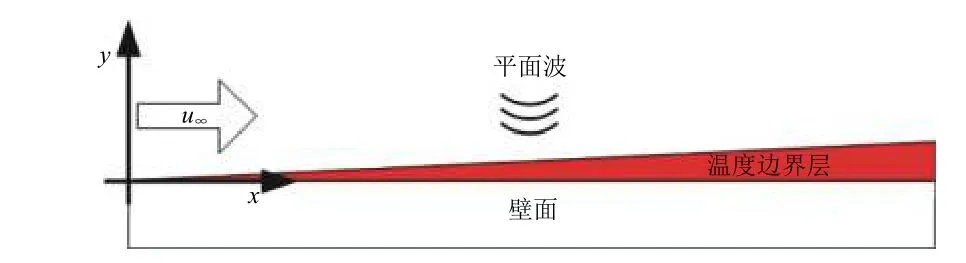
图4 平面波入射平板温度边界层简化模型Fig.4 Simplified model of soundwave skimming over temperature boundary layer of a flat panel

在声传播方向采用二阶精度的中心差分法对式(13)进行离散，得到差分方程

其中：pb1为壁面声压；pb2、pb3为紧贴壁面的两层网格处的声压。

沿声波传播方向等距划分网格，取Δx=0.1 mm，将第2 章求解得到的温度边界层内的温度分布转化为非均匀介质密度并在各层网格上进行离散，然后采用MatLab 编程求解非均匀介质声传播方程的有限差分形式，得到声压在各网格节点上的分布。

4 计算结果及分析

取温度边界层边缘处声场p0=2000 Pa 的白噪声谱，以第3 章所述有限差分法求解壁面附近声场，并与同样边界条件下均匀介质（T=300 K）壁面附近声场的有限差分法求解结果进行对比。

图5 所示为壁面中心位置的声压。由图可见，在温度边界层的影响下，壁面中心位置声压相对于均匀介质减弱了，且在高频部分更为明显，也就是说，高频声波在穿越非均匀介质时衰减更为显著。

图6 所示为声波频率f =10 000 Hz 时，有无温度边界层条件下近壁面附近的声压分布对比，横坐标(1-y/δT)表示由温度边界层边缘指向壁面方向的空间位置。由图可见，由于壁面反射，声压级随距壁面距离的减小而增大，有温度边界层时曲线斜率明显减小，显示出温度边界层对近壁面声场的削弱作用——在温度边界层影响下，壁面上的声压相对于均匀介质减小约1100 Pa（声压级减小约3 dB）。

图5 壁面中心位置声压Fig.5 Sound pressure in the center of the wall

图6 温度边界层内声压分布（f=10 000 Hz）Fig.6 Sound field distributions in the temperature boundary layer (f=10 000 Hz)

5 结束语

本文建立了声波穿过温度边界层的理论模型，采用边界层积分法求出了热噪声试验中常温气体掠过高温壁板时温度边界层内的温度分布，在此基础上采用有限差分方法对固壁边界条件下非均匀介质声传播方程进行数值求解。结果表明：

1）温度边界层影响近壁面声压分布，壁面附近声压相对于无温度边界层时有所减弱；

2）温度边界层对壁面声压的衰减作用随声波频率增大而增大，在入射声波频率为10 000 Hz 时衰减最为明显，比无温度边界层存在时声压减小约1000 Pa，声压级减小约3 dB。

以上数值计算结果与试验观测现象相符。因此，开展热噪声试验时，应考虑温度边界层对近壁面声场的削弱效应，并通过数值计算或调试试验修正热环境影响下的噪声加载条件。

本文求解时对非均匀介质声传播的理论模型进行了简化，事实上求解的是平面波穿过非均匀层状介质问题。后续将把计算域扩展到二维平面中，考虑声波透射方向，对整个平板温度边界层内的声场进行求解，并开展试验分析验证，对理论计算结果进行修正。