天宫飞行器过渡流区高超声速绕流N-S/DSMC 耦合计算
李中华,党雷宁,李志辉,2,李绪国
(1. 中国空气动力研究与发展中心超高速空气动力研究所, 绵阳621000;2. 北京航空航天大学 北京前沿创新中心国家计算流力学实验室,北京100191)
1 引言
天宫飞行器陨落再入大气层过程会经历稀薄过渡流区。 在强烈的气动力/热作用下会发生解体并产生大量碎片,其中一部分碎片在空中被完全烧毁,其余存活下来的残骸碎片会落到地面。 过渡流区的气动力、热特性的准确预测对航天器解体及其残骸碎片陨落的预报至关重要。
过渡流区的流动无论试验还是数值计算均难于处理[1-2]。 在数值仿真方面,基于连续流的CFD 技术[3-4]和广泛应用于稀薄流的DSMC 方法在过渡流区均会遇到各自的问题[5-7]。 在求解稀薄效应很重的流动非平衡问题时,连续流方程会失效,CFD 的结果可能会在流场和物面力/热参数等计算方面产生比较大的误差;DSMC 方法受网格尺寸和时间步长的限制,计算效率很低,难以实现有效模拟[8-9]。 过去在计算机不够先进的情况下,过渡流区气动特性的计算主要以当地化方法的工程计算为主。
近年来,随着高性能计算机与数值计算技术的发展,在过渡流区,基于Boltzmann 模型方程的气体动理论统一算法已研究建立[10-11],并取得了较好的效果。 但其计算量巨大,应用受到一定的限制。 另外一种途径是连续流/稀薄流的耦合算法[12]。 基于CFD 和DSMC 方法的N-S/DSMC 耦合算法,能够发挥各自的优点,扩展CFD 和DSMC方法的应用范围,提高DSMC 方法在模拟过渡区流动的计算效率[13-14]。 但是,对于耦合方法的研究,多以二维/轴对称简单外形为主,研究耦合算法的机理问题,对于三维复杂流动问题,研究文献很少[15]。
本文基于MPC(Modular Particle-Continuum)耦合处理方法[16-18],建立一种适于三维复杂外形飞行器过渡流区高超声速绕流问题的N-S/DSMC耦合算法;并利用该耦合计算方法,对天宫外形体在低密度不同克努森数(Knudsen,Kn)条件下的绕流进行数值计算研究,通过与相关风洞实验和计算结果的比较,验证所建N-S/DSMC 耦合模型算法的有效性。
2 数值模拟方法
本文采用MPC 耦合处理技术,不需要对CFD和DSMC 程序做改动,直接在2 个独立的程序模块外部加入网格和信息交换的计算模块,以实现N-S/DSMC 的耦合计算[17-18]。
把整个流场分为连续流和稀薄流区(图1)。在连续流区域,采用时间一阶、空间二阶的隐式NND 格式求解式(1)所示三维非定常可压缩N-S方程[3]:

式中, U 为守恒变量矢量;E、F、G 为无粘通量矢量;Ev、Fv、Gv为粘性通量矢量。

图1 N-S/DSMC 耦合算法分区示意图Fig.1 Sketch of N-S/DSMC hybrid method
在稀薄流区域,采用DSMC 方法求解非平衡流场[8,19-20]。 采用式(2)所示当地Kn 数判断连续流方程的失效问题[11,13]:

式中,λ 为当地流场气体分子平均自由程;Q为当地流场宏观流动参数,可以是压力、密度或温度。 取梯度最大的流动参数来计算Knl。 当Knl≥0.02 时,在耦合边界上,流动已经开始出现非平衡现象,此时速度分布函数已经不再符合Maxwell 平衡分布,认为连续流方程失效,可以采用Chapman-Enskog 分布来描述。
对于偏离Maxwell 分布的非平衡分布,其一阶展开如式(3)[21]:
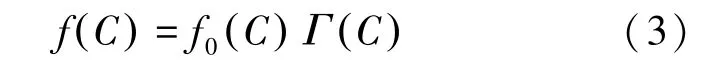
式中,C 为无量纲化的分子热运动速度, C =c/(2kT/m)1/2。 Г(C)为偏离度,满足式(4):

本文基于Maxwell 分布的速度采样方法,在边界面上给出符合Chapman-Enskog 分布的分子速度[21],根据当地的非平衡度,采用“拒绝-接受”的随机筛选准则,产生符合Chapman-Enskog 分布的分子速度。 步骤如下:

2)设置幅度参数A =1 +30B;
3)根据Maxwell 分布产生一个速度矢量Ctry;
4)产生一个随机数Rf。 如果ARf≤Γ(C),接受Ctry;否则,返回到第3 步,产生新的Ctry;
5)给出分子速度c =(2kT/m)1/2Ctry+u。
由于DSMC 方法存在较大的统计波动,这些统计波动如果传递到CFD 求解区域,可能会导致CFD 求解不稳定。 为了抑制DSMC 方法的统计波动对CFD 计算的影响,本文发展了基于亚松弛的收敛处理技术。 在每个时间点j 上,某个网格中由DSMC 方法模拟得到的宏观流动参数为Qj(包括ρ、u、v、w、T),传递给CFD 的参数与上一步的参数进行式(4)所示加权平均:
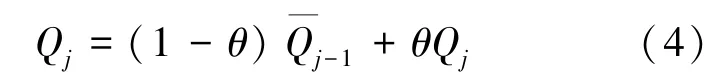
式中,θ 为网格中新参数的比较小的权重(本文取θ=0.02);相应地,(1-θ)是比较大的权重。
3 算例结果与讨论
3.1 天宫两舱体低密度风洞试验耦合计算验证
采用前述N-S/DSMC 耦合模型算法计算了天宫两舱结构体外形在稀薄过渡流区不同来流条件下的试验状态。 低密度风洞试验状态见表1。 试验气体为氮气(N2)。 每个试验状态分别计算-2°~25°迎角绕流流场。

表1 两舱体外形过渡流区试验状态Table 1 Test cases of two-module configuration
两舱体0°迎角典型流场压力分布云图如图2。 头部端面形成主激波,主激波打在舱体肩部,形成次激波,在肩部产生仅次于驻点区的高压和高热流集聚效应,因两舱体外形的巨大尺度,在背风区尾部出现较大范围的低压真空区。
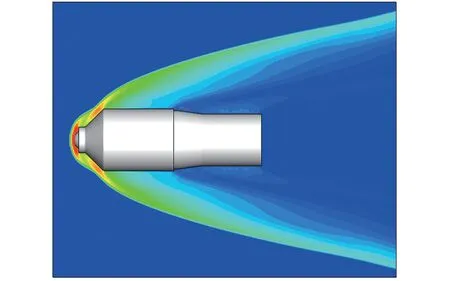
图2 N-S/DSMC 计算天宫两舱体流场压力分布(状态1)Fig.2 Pressure distribution of two-module body calculated by N-S/DSMC (case1)
气动力特性耦合计算与试验结果的比较情况如图3。 对于轴向力系数CA,两个试验状态差别比较明显。 在试验参数范围内,CA随着稀薄效应的增大而增加。 法向力系数CN和俯仰力矩系数(绝对值)Cm0随迎角增加而增加,而随稀薄度变化不大。 压心系数随稀薄度的变化也较小。 这些均符合过渡流区气动力特性变化规律。 图3 所示本文算法计算与低密度风洞实验2 种结果的对比表明,耦合算法结果与试验结果吻合很好,迎角越小,耦合算法结果与低密度风洞实验吻合越好。

图3 不同状态下两舱体气动特性计算与风洞试验比较Fig.3 Comparison of aerodynamic characteristics between the present computation and the windtunnel experiment for various cases of twomodule configuration
3.2 天宫多次解体残骸两体间干扰流场耦合计算
天宫多次解体后,会产生各种类型的残骸碎片,相互之间的流场会有干扰。 简单起见,本文计算了球(D =100 mm)和球柱(D =100 mm、L =200 mm)2 种外形在表2 所示来流条件决定的流场干扰特性。 两体的位置为头部并齐,平行放置,轴线间距离为d。

表2 两体干扰流场状态计算参数Table 2 Cases of interfere flow field
不同干扰距离条件下两个球体干扰压力场等值线云图分布如图4。 在d/D =1.25 条件下,激波在对称面上形成干扰激波,干扰激波很强,打在球体表面后形成反射激波,并在对称面上再次反射,形成复杂波系。 在d/D =1.5 条件下,反射激波与尾流区的膨胀波相互作用,在尾流区形成复杂波系。
两体干扰对气动特性的影响如图5。 从图中可以看出,随着稀薄度的增大,轴向力系数增加。在Ma =10 的条件下,当d/D =1.25 时,两体之间的干扰对气动特性有一定影响,两种稀薄度条件下,CA均有一定下降,这是因为干扰激波打在球体的下、后表面,在下、后表面产生高压区域(参见图4 所示),向前产生一定推力,使得CA下降。这个高压区域同时产生法向力和俯仰力矩,并使压心系数后移。 从CN系数随不同来流Kn 数变化来看,稀薄度越大,干扰的影响越大。 当d/D≥1.5 时,干扰对气动特性基本不产生影响。 这为空气动力融合轨道数值预报提供实时计算工程设计准则。

图4 天宫解体残骸球体绕流不同间距干扰流场(Case2)Fig.4 Interference flow field between spheres of varies distances (case2)

图5 球体干扰对气动特性的影响Fig.5 Effects of interference on aerodynamic characteristics around two side-by-side spheres
图6 是天宫多次解体残骸简化物两个并排球柱体绕流的流场结构。 d/D =1.25 时,干扰激波在对称面和柱体间进行多次反射,残骸间绕流干扰严重;d/D=1.5 时,干扰激波在对称面和柱体间只有一次反射,残骸间绕流干扰迅速减小。
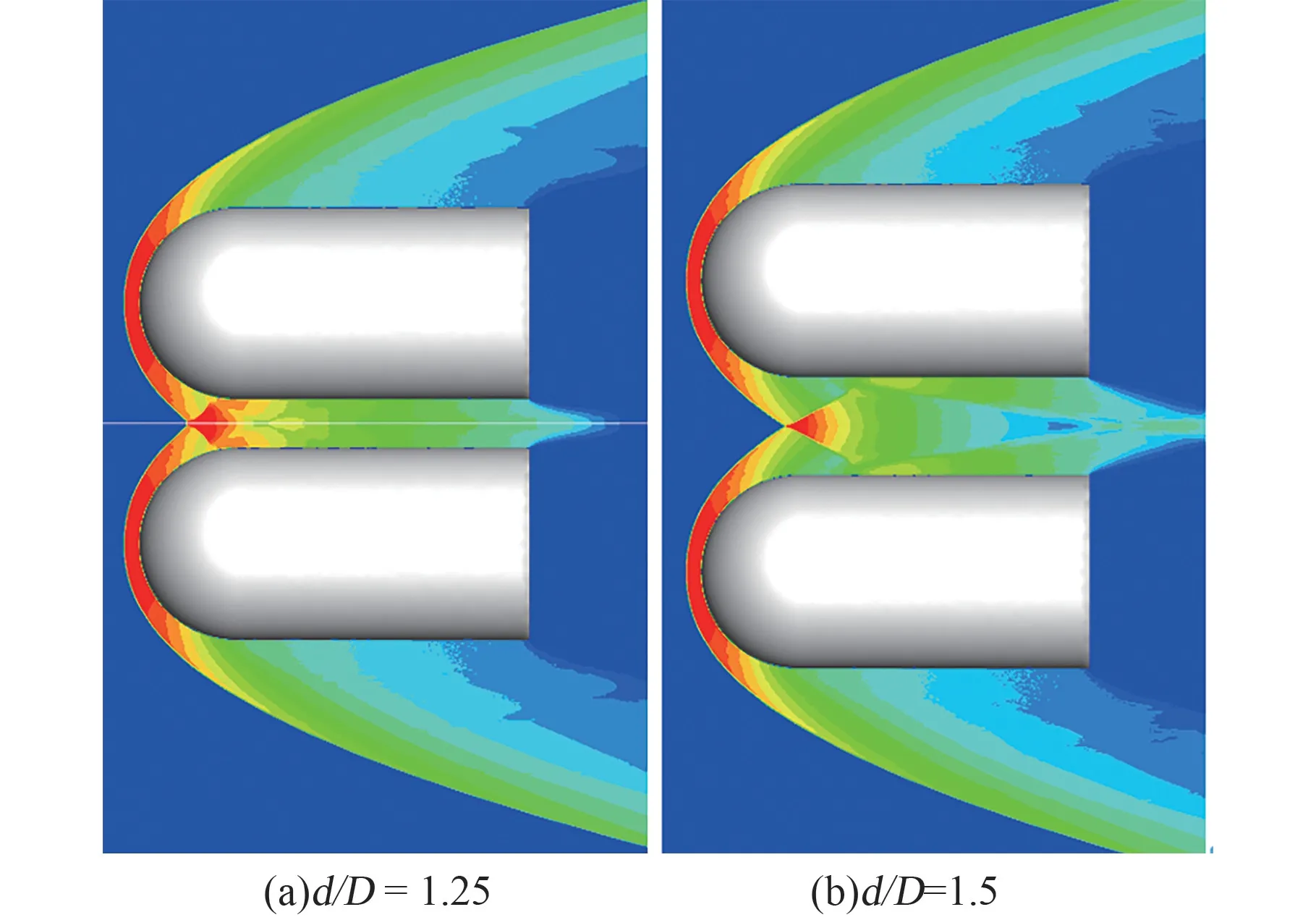
图6 球柱体绕流不同间距干扰流场(Case2)Fig.6 Interference flow field between sphere-poles of varies distances (case2)
图7 绘出干扰对气动特性的影响。 从图中可以看出,与球体类似,随着稀薄度的增大,轴向力系数增加。 在Ma =10 的来流条件下,当d/D =1.25 时,两体之间的干扰对气动特性有一定影响,两种稀薄度条件下,干扰距离越小,两体间绕流干扰越严重。 残骸间干扰使CA、CN、Cm增加,压心位置Xcp后移;当d/D=2 时,干扰基本不对气动特性产生影响。

图7 球柱体干扰对气动特性的影响Fig.7 Effects of interference on the aerodynamic characteristics of sphere-poles
对以上结果分析表明:物体的形状、残骸间距离、来流稀薄条件等因素会对残骸碎片气动特性产生不同的干扰影响,基于表2 计算条件,一般在两体相距1.5 倍之外,残骸碎片间绕流干扰在再入解体飞行航迹数值预报设计中,可以忽略不计其对气动特性的影响。
4 结论
1) 通过对CFD 和DSMC 方法计算程序进行基于网格与信息交换的双向耦合设计,发展了求解过渡流区高超声速三维绕流问题的N-S/DSMC耦合算法。
2) 采用耦合算法,对天宫飞行器两舱体在低密度风洞试验条件下的气动力特性开展了仿真,与试验结果进行对比,验证了本文所建立的耦合算法对数值求解类天宫飞行器服役期满再入解体过程所产生残骸碎片多体绕流干扰的可靠可行性。
3) 通过对天宫解体残骸碎片简化外形的两体(球体、球柱体)干扰流场进行仿真计算,结果表明,对于球、球柱这类简化外形,在一定的距离范围内,两体干扰会对气动特性产生很强的影响,随着两体间隔距离的增大,如简单球体间隔1.5倍、球柱体间隔2 倍直径,残骸碎片间绕流干扰引起的气动特性影响可以忽略不计,为天宫飞行器实际再入解体气动融合结构/轨道数值预报提供重要设计规范标准。

