基于神经网络的房地产销售额预测

赵云柯

摘  要：最近十几年里普通民众对房价的涨跌始终保持着很高的关注度，而这一关注度或许可以通过百度搜索指数得到量化。

而另一个面向，我们相信房地产销售额的波动会与多数民众某些经济行为的特性发生关联。这或许可以通过电影排片场次得到侧面的体现。

基于上述思考，我们希望利用神经网络，通过以某一周“上海房价”的百度搜索指数、上海电影排片场次和上海房地产平均单位面积销售价格为自变量建立模型，来拟合计算得出该周上海房地产销售额。

关键词：神经网络;机器学习;多元回归;房地产

一、具体问题及分析

1）收集并整理从2016年到2019年每周“上海房价”百度搜索指数、每周上海电影排片场次、每周上海房地产单位面积平均售价，每周上海房地产销售额的数据，并制作样本与测试集。

2）搭建并使用1）中的数据训练基于深度学习的神经网络模型，利用均方差损失函数和梯度下降法拟合求解回归模型。

3）在2）所得出的回归模型当中，解释结果模型的各自变量对上海房地产销售额的影响，解释其在现实生活中的含义并进行相关探讨。

二、模型的假设

本文所要研究的是百度搜索指数、电影排片场次及平均銷售价格对于房地产销售总额的影响。对于本文所考虑的问题，基础的线性回归问题不足以拟合出贴合度较好的函数，因此我们将线性关系转为高次的函数。考虑到三个自变量之间关联度并不高，我们将模型定义为：

对应索引i，即：

同线性回归问题一致，我们采用平方误差函数作为损失函数，小批量随机梯度下降法作为优化算法。可以得出索引i的损失函数为：

因此同线性回归问题，一次迭代中的平均损失函数为：

即：

显然，每次迭代对于参数调整的优化方法为：

对于超参数的设置，我将迭代次数定为100000次，初始学习率定为0.1。随着迭代的进行，我使用了类似于离散下降的方式来动态调整学习率：当该次迭代损失函数优于上次时，学习率增长上次的5%;当该次迭代损失函数劣于上次时，学习率减少上次的50%，且保证学习率的波动范围一直处在0.01与0.8之间。如此设置，既保证了迭代的效率，使得模型能够在有限次内高效地得出较优解，也确保了准确度，使得函数不会波动过于动荡。

将所有数据进行整合后，我们令2016年1月4日到1月10日为第1周，将第1周至第200周的数据作为样本，其余数据作为测试集。

三、模型拟合结果

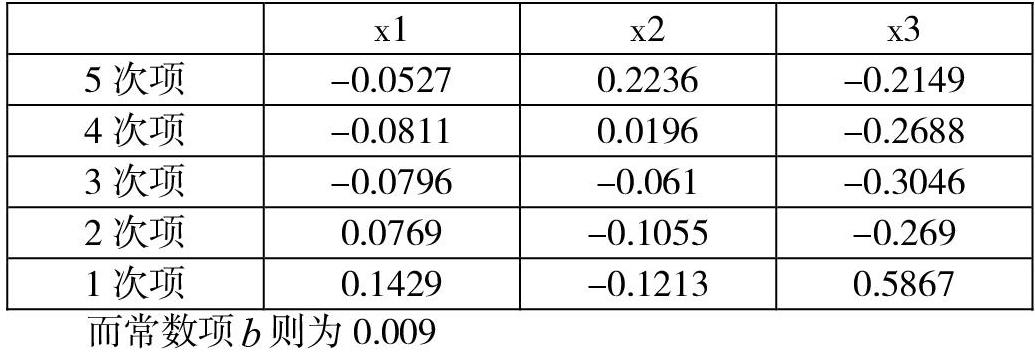
我们设百度搜索指数为x1，电影排片场次为x2，单位面积平均售价为x3。通过python编程，可知w参数对应不同自变量不同次项分别为：

四、回归模型拟合结果分析

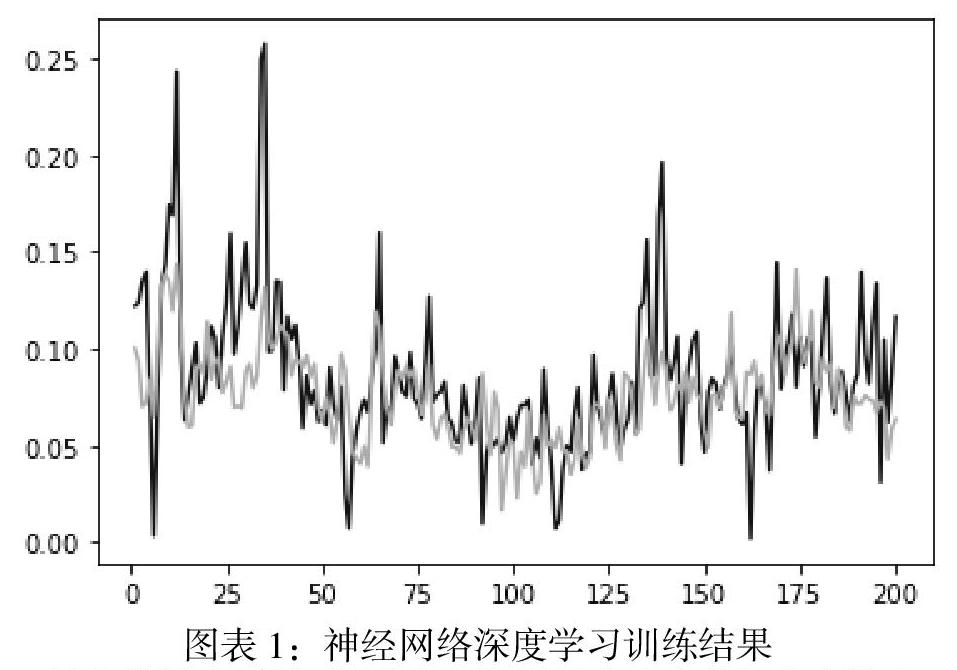
机器学习所得到的回归模型平均损失函数值为0.000476。相比之下，没有经历过任何优化的初始模型损失函数值约为0.001，可以发现精确度得到了显著的提升。对于样本而言，我们的模型剔除了样本中的极端值，预测结果的平均值与样本因变量接近，而方差比样本更小，相较于样本更为平滑连贯，两者的比对图形如下图1：

其中横轴为周数，纵轴为上海每周房地产总销售额除以10，000后的商。蓝色为实际值的函数，黄色为预测值的函数。蓝色几个异常的极低点，都是发生在春节期间。由于在春节放假期间几乎不会有任何房屋交易，所以在这一非经济和关注度条件的影响下，蓝色曲线的值会异常的低。社会文化因素也导致蓝色实际值出现了个别因变量极高的数据，这些都无法被我们基于经济水平和大众关注的模型预测出来。但依然，我们可以看出两者的趋势大致吻合，总体来说依旧具有一定的适用性。

而对于测试集所计算出的预测值与实际值，即使测试集中包含了2020年春节时期的数据，具有显著社会文化因素的影响，但两者差距在5%显著性对应的z分数1.64个标准差之内的占比依旧超过了80%。可以看出，即使对于在样本时间段之外的测试集，我们的模型依旧拥有客观的正确率。

五、结论与展望

本文针对百度搜索指数、电影排片场次及平均销售价格对于房地产销售总额的影响，提出了基于神经网络利用机器学习对各参数进行高次函数建模拟合的方法，并通过对百度搜索指数、电影排片场次、平均销售价格与房地产销售总额建立函数关系进行了应用，为未来利用不同自变量对因变量的预测提供了指导。本文获得的主要结论如下：

（1）基于单层神经网络，采用平方误差函数作为损失函数，小批量随机梯度下降法作为优化算法，近似离散下降的方式动态调整学习率，进而建立了以百度搜索指数、电影排片场次及平均销售价格为自变量，房地产销售总额为因变量的5次函数。所建模型适用于与处理后单位相同，且位于上海的数据。

（2）以房地产销售总额为对象，基于神经网络实践了机器学习模型在互相之间关系较浅的多特征拟合问题的应用。本文所建模型的预测值与实际值虽然有一定的误差，但函数更为平缓，有利于对于样本时期之外的数据进行预测。同时小批量随机梯度下降法与动态调整学习率的使用使得模型效率较高，100000次迭代在普通的家用笔记本电脑上可以在约30分钟内完成。

当然，本文的模型由于仅仅考虑了经济水平与大众购买意愿这两个因素，在实际使用时出于社会文化因素等原因的影响会出现一定的偏差。若要完全了解并构建出能够精准预测房地产销售额的多特征模型，我们仍需在未来投入大量的工作，考虑更多的因素，并展开更深入的研究。

参考文献

[1]  基于MATLAB的房价预测与调控模型研究[J]. 成鸿飞，王江鹏，余琴.科协论坛（下半月）. 2010（06）

[2]  基于BP神经网络的房价预测[D]. 崔庆都.西南石油大学 2011

[3]  动手学深度学习[M]. 阿斯顿·张.人民邮电出版社.2019