基于CFD-DEM 耦合的条缝出流自由下落流场特性研究

伍吉富 孙宏发 张静

西安建筑科技大学建筑设备科学与工程学院

在工业生产过程中，散料在重力作用下自由下落至料堆或传送带时，会散发大量的粉尘，使得地下环境受到污染，不仅会影响设备的运行，更会危及工作人员的健康。上世纪60 年代以来，各国学者对散料颗粒自由下落过程进行了大量的研究，Hemeon[1]基于单颗粒在静止空气中下落最先提出了预测自由下落微粒流的卷吸空气量模型。Cooper[2]对卷吸空气量进行了更深一步的研究，从理论分析提出了不同颗粒粒径的卷吸空气量模型。Ogata[3]通过实验研究了颗粒流的速度分布特性，发现颗粒流轴心速度大于单颗粒的沉降速度，并给出了不同颗粒雷诺数下的卷吸空气量模型。随着计算能力及求解精度的快速提升，采用CFD模拟进行颗粒下落的研究已较为普遍[4-6]。现有研究主要针对圆孔出流的点状尘源，鲜有对条缝出流线状尘源的研究，且相关模拟研究大都忽略了颗粒碰撞的影响，文献[7]指出颗粒体积分数即便只有0.04%，颗粒碰撞的影响依旧不能被忽略。基于计算流体力学（CFD）与离散元素法[8]（DEM）的CFD-DEM 耦合模型[9]能更好地考虑颗粒之间的碰撞，因此本文采用CFD-DEM耦合模型对线状尘源的条缝出流不同出口长度及粒径的自由下落过程进行了研究，从微观尺度分析微粒羽流运动及卷吸空气的流场特性，以期为通风除尘设计提供相关指导。

1 CFD-DEM 耦合模型

近年来，CFD-DEM 耦合模型作为一种全新的仿真方法已经得到广泛应用。该模型能够更好的模拟颗粒与颗粒，颗粒与壁面之间的碰撞，获得颗粒和流场的微观信息，保证对颗粒运动的精确模拟，被誉为最有前途的气固两相流模拟方法之一[10]。

1.1 流体相控制方程

流体相基于连续介质模型，考虑颗粒相作用的流体运动连续性方程和动量方程分别为：

式中：ρf，uf，P，τ 分别代表颗粒的密度，速度，压力以及应力张量；g 为重力加速度；ε 为空隙度，是网格单元中流体所占的体积分数；S 为动量汇，是作用在网格单元内流体阻力的总和。

1.2 颗粒相控制方程

颗粒相的运动基于离散元素法，根据牛顿第二定律求解颗粒运动方程：

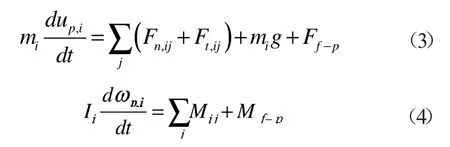
式中：mi，Ii，up,i，ωp,i分别为颗粒i 的质量，转动惯量，平移和旋转速度；Fn,ij，Ft,ij是颗粒i，j 之间的法向和切向接触阻力；Mij是颗粒之间的接触扭矩；Ff-p，Mf-p分别是流体对颗粒的作用力和作用力矩。文献[4]指出在自由下落的过程中Saffman 升力对颗粒流的扩散有着重要的影响，因此在本文研究中，流体对颗粒的作用力主要考虑阻力和Saffman 升力。

2 模型建立及验证

2.1 物理模型建立

在实际工程中，条缝出流更为普遍。建立如图1 所示颗粒条缝出流自由下落的物理模型和三维坐标系。计算区域为一个长方体，模型尺寸为600 mm×600 mm×1000 mm（长×宽×高）。在模型顶部设置颗粒流出口，高为5 mm，宽度b 为2 mm，长度l 随模拟工况变化。采用ICEM 软件对模型进行计结构化网格划分，并对颗粒流出口及下落部分进行局部网格加密。

图1 颗粒条缝出流自由下落物理模型

2.2 边界条件及模拟工况设置

对流体相，颗粒流出口设为速度入口边界（Velocity inlet），取值0.001 m/s[6]，出流口侧面以及底面为墙边界（Wall），计算区域其他部分设置为自由出流边界（Outflow）。对颗粒相，设置颗粒初速为0 m/s，颗粒的材料力学性质详见表1[3，11-13]，接触参数详见表2[14-15]。

表1 材料力学性质

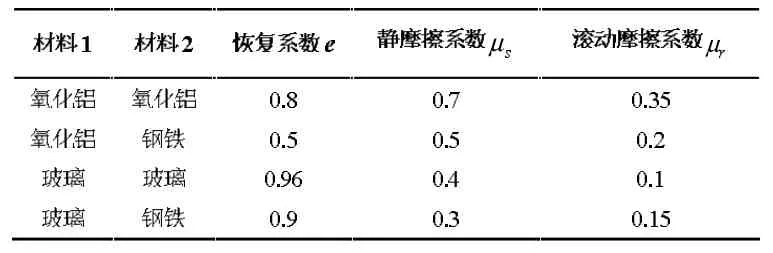
表2 接触参数

为研究不同出口尺寸和粒径对颗粒流场特性的影响，进行了多工况模拟，不同工况质量流量的计算公式[16]如下：

式中：mp是颗粒流的质量流量；ρb是颗粒的堆积密度；A0是孔口面积；b 是颗粒出流宽度；dp则是颗粒的平均粒径。

选取工业散料氧化铝颗粒进行分析，设置不同的条缝出流口尺寸，并参照文献[5]设置颗粒粒径分别为300 μm，400 μm，500 μm，具体模拟工况见表3。

表3 模拟计算工况

2.3 湍流模型选择及验证

前人对圆孔出流自由下落过程进行了许多研究，为了验证CFD-DEM 耦合模型的在自由下落研究的可行性，对圆孔出流过程进行验证。

在颗粒流下落研究中常用的湍流模型[17]有：标准k-ε 模型（SKE）、重整化k-ε 模型（RNG）、可实现的k-ε 模型（RKE），雷诺应力模型（RSM）以及剪切应力输运模型(SST)。Ogata 等人通过实验研究了不同孔径自由下落颗粒流的速度分布[3-4]，参照实验设置出流圆孔直径D 为4 mm，采用平均粒径为454 μm（几何标准差为0.116）玻璃微珠进行模拟，玻璃微珠的初速度为0.77 m/s，堆积密度ρb为1460 kg/m3，质量流量为0.002 kg/s。为选择合适的湍流模型，采用这五种湍流模型与Ogata 的实验数据进行对比，如图2（a）所示。从图中可以看出，不同湍流模型与实验值的变化规律基本一致，其平均预测偏差分别为6.7%、5.7%、5.8%、4.6%、7.2%，RSM 雷诺应力湍流模型的偏差最小，因此后续数值模拟选用RSM 湍流模型进行分析。

针对圆孔出流自由下落过程Hemeon[1]，Cooper[2]及Ogata[3，5]等先后提出了不同的卷吸空气量模型。采用氧化铝颗粒进行分析，粒径取为300 μm，质量流量取为0.0015 kg/s[18]，以对流体相卷吸空气进行验证。在某一高度截面上，对颗粒流卷吸直径内的气流速度进行积分计算模拟所得的卷吸空气量，并将其与理论计算值进行对比，详见图2（b）。可以看出，Ogata 提出的卷吸空气模型计算值相比于Hemeon 和Cooper 的计算值要大，这可能是因为Hemeon 低估了颗粒群中单颗粒的速度，模拟值与Ogata 提出的卷吸空气模型拟合的较好，为CFD-DEM 耦合模型对自由下落流体相的模拟提供了理论支持。

图2 模型验证

3 模拟结果及分析

3.1 不同下落高度流场特性分析

图3 和图4 分别给出了工况1 不同下落高度颗粒流的速度分布图。图3 所示，由于颗粒流核心区大，在z=100 mm 处Y 方向核心区颗粒速度大小基本一致，随着下落高度的增加，颗粒流逸散宽度增大且短边方向增长更为明显，速度也逐渐增大，但增长趋缓。相同高度不同方向上颗粒的速度分布见图4，在z=500 mm处不同方向上的颗粒速度分布差异很大，而在z=900 mm 处不同方向上速度分布趋于一致，这和三维射流在轴对称衰减区空气速度剖面相似的结论相仿[19]。

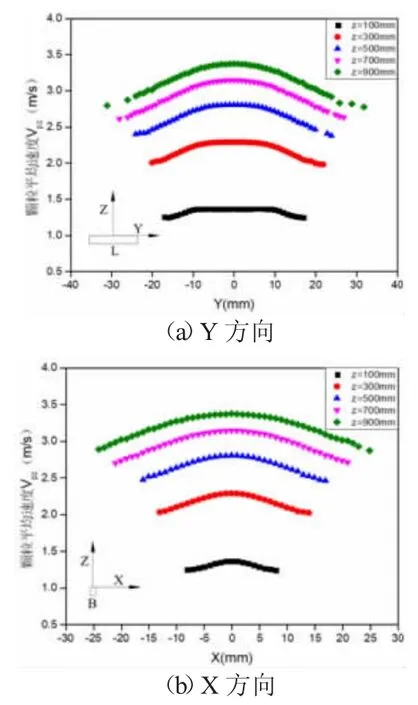
图3 不同高度颗粒速度

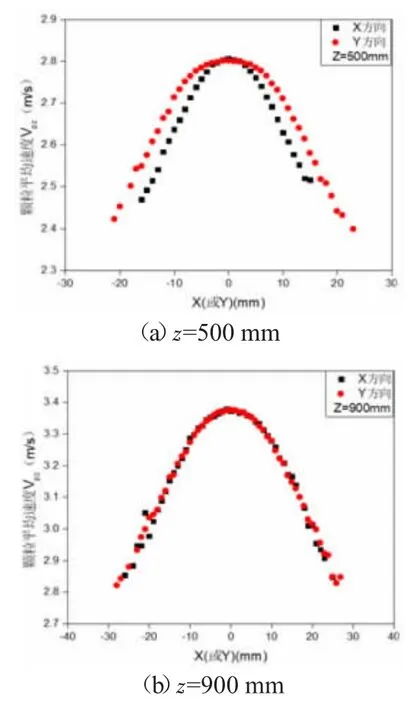
图4 不同方向颗粒速度

图5 和图6 分别给出了工况1 不同下落高度颗粒流卷吸空气速度分布图。由图5 可知，卷吸空气宽度远大于颗粒流逸散宽度，且随着下落高度增加而增大，但卷吸空气轴心速度先增大后减小。这是因为在下落初始阶段，颗粒流向两侧的逸散宽度相对较小，颗粒对单位流体的动量汇随着颗粒速度的增大而增大，而随着颗粒逸散宽度的增大，颗粒速度增长趋缓，作用在单位流体上的动量汇S 逐渐减少，因此卷吸空气速度减小。图6 所示，在远离出口的z=500 mm 和z=900 mm 处不同方向上卷吸空气速度分布基本趋于一致。

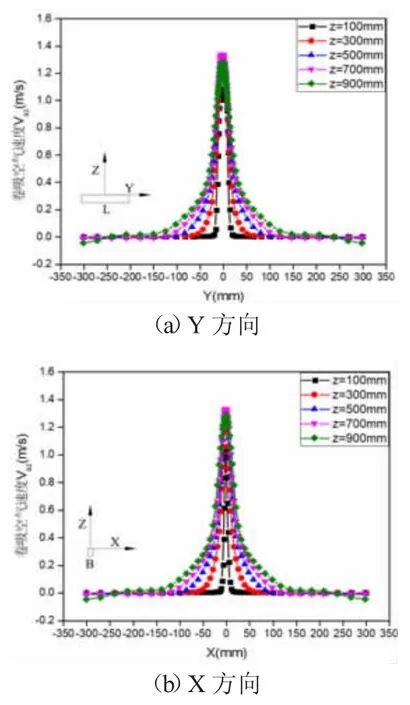
图5 不同高度卷吸空气速度分布

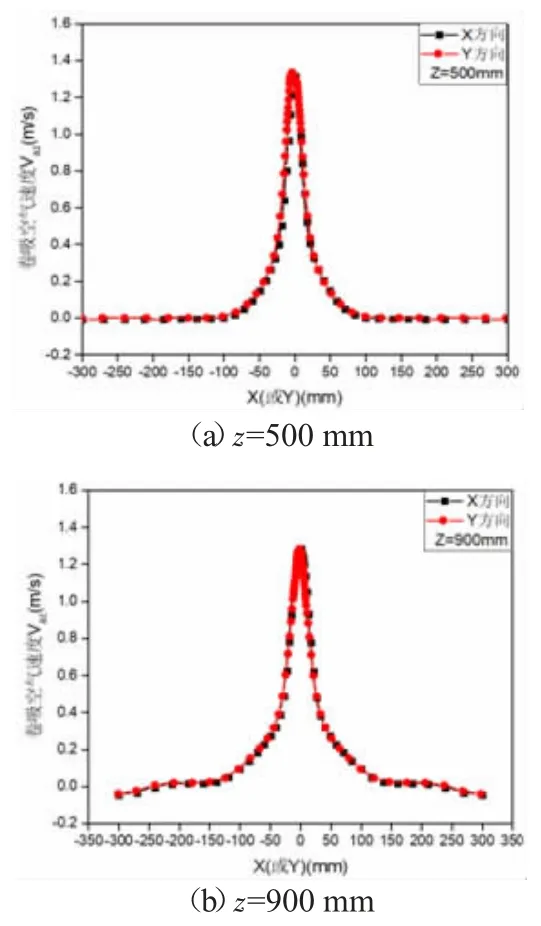
图6 不同方向卷吸空气速度分布

3.2 不同出口长度流场特性分析

对于不同出口长度20 mm，30 mm，40 mm，图7给出了核心区颗粒流和卷吸空气速度的对比。考虑到不同方向颗粒和卷吸空气轴心速度一致，后续对比只从X 方向进行分析。由图7 可知，出口长度越大颗粒和卷吸空气速度越大，并在l＞30 mm 后趋于定值。其原因是，出口长度越大颗粒流核心区越大，更不易向外扩散，受空气阻力的影响越小，但随着出口长度不断增大，颗粒流核心区受空气影响不明显因而颗粒和卷吸空气速度逐渐趋于定值。

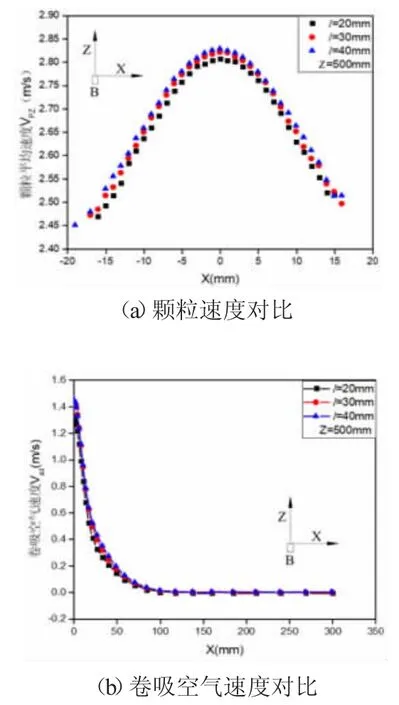
图7 不同出口长度颗粒和卷吸空气速度对比

参考Wypych 等人[20]提出的方法，结合单位质量流量的卷吸空气量进行分析。由图8 可知卷吸空气量随出口长度增加而增大，但单位质量流量卷吸空气量随出口长度增加而减小。这可能是因为颗粒流核心区越大，孔隙度越小，颗粒与空气接触面积越小，所以单位质量流量卷吸空气量越少。

图8 不同出流长度卷吸空气量对比

3.3 不同颗粒直径流场特性分析

针对粒径分别为300 μm，400 μm，500 μm 的氧化铝颗粒，核心区颗粒和卷吸空气速度的对比分析见图9。由图9 可知，颗粒粒径越大颗粒速度越大，卷吸空气速度越小。这是由于颗粒粒径越大质量流量越小，颗粒数越少，所受空气阻力越小，因此颗粒速度越大，同时流体内颗粒数越少，卷吸空气速度越小。

不同粒径卷吸空气量对比如图10 所示，可以看出相同高度处粒径越小颗粒的卷吸空气量越大，且单位质量流量卷吸空气量也随粒径减小而增大。这是因为在单位质量流量下，粒径越小颗粒数越多，颗粒传递给单位体积流体的动量汇S 越多，所以单位质量流量卷吸空气量也越大。

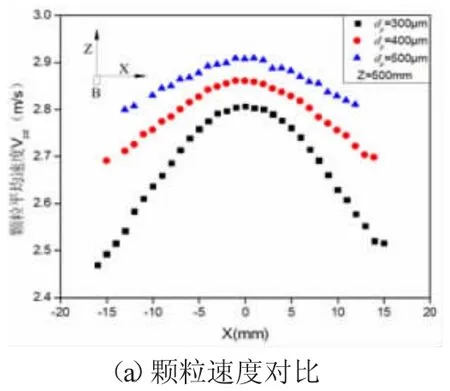
图9 不同粒径颗粒和卷吸空气速度对比

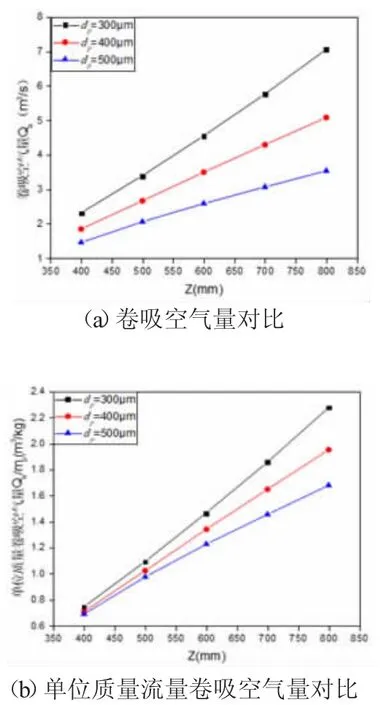
图10 不同粒径卷吸空气量对比

4 结论

本文采用基于计算流体力学和离散元素法的CFD-DEM 耦合方法，研究了条缝出流不同下落高度，出口长度及粒径对流场的影响，得到了以下结论：

1）条缝出流的逸散宽度在短边方向增长速度相比长边更快。在z=500 mm 处不同方向上颗粒速度分布差异较大，而在z=900 mm 处不同方向的速度分布基本趋于一致。远离出口处相同高度不同方向上的卷吸空气速度分布趋于一致。

2）随着出口长度度的增加，颗粒和卷吸空气的速度逐渐增大并在l＞30 mm 后趋于定值。粒径越大，颗粒速度越大，而卷吸空气速度越小。

3）对于实际工程设计，卷吸空气量随出口长度的增大而增大，但单位质量流量的卷吸空气量随之减小。粒径越小，卷吸空气量和单位质量流量的卷吸空气量越大。