基于大数据挖掘技术不停机间抽工作制度优化 ——以大庆油田为例

高 翔，王云峰，刘海波

（1.中国石油大庆油田有限责任公司采油工程研究院，黑龙江大庆 163453；2.中国石油大庆油田有限责任公司第九采油厂工程技术大队，黑龙江大庆 163511）

随着大庆油田开发进入中后期，低产液、低泵 效、低流压井逐年上升，这部分井存在着系统效率 低、能耗大、设备磨损严重等问题[1-3]。为提高低效井的系统效率，达到节能降耗的目的，通常采用间抽采油技术[4-5]。但在实际生产过程中，采用常规间抽技术往往因为停井时间长导致卡泵故障、井底流压上升，从而影响油井产量。相关研究表明，常规间抽技术平均影响油井产量0.1 m3/d，部分井潜力未得到充分发挥[6]。在综合考虑常规间抽技术缺点的基础上，相关工程技术人员提出一种抽油机不停机间抽技术。目前，大庆油田累计应用不停机间抽技术千余口井，与常规间抽技术相比，吨液百米耗电降低明显，系统效率显著提高，应用前景广阔[7]。

不停机间抽技术应用过程中，工作制度的确定是最关键的部分[8]。一般情况下，主要参考单井地质特征和供液能力，以油井产能为最大目标，结合IPR（流入动态生产曲线）确定合理流压，通过持续观察动液面变化，最终确定最优的不停机间抽采油工作制度。但是该种方法需要对每口井工作制度进行多次试验和反复验证，实际操作性不强，生产单位通常依据沉没度和产液情况，将运行工作制度定为若干种（表1），从而大大降低了单井个性化设计强度，也减弱了不停机间抽技术的应用效果。

近几年来，数字化、智能化、智慧化油田的建设将油田带到了“大数据、人工智能”时代[9]，大数据挖掘技术作为机器学习、人工智能的基础，同样也开始应用到油气田勘探开发的各个领域[10-13]。2012年，石广仁教授介绍了八大类数据挖掘算法，并通过34 个应用实例对算法的应用范围及条件、基本原理和完整计算方法进行了适用性比较[14]；2015 年，檀朝东等人系统总结了大数据挖掘技术在石油工程的应用前景[15]；2016 年，孙敬等人采用大数据挖掘技术建立的产能评价方程所预测的气井产量与实际产量相比，精度可以达到90%[16]；2018 年，李大伟等人开展了油气勘探开发常用数据挖掘算法优选工作，认为最优的回归算法是反向传播神经网络（BPNN），最优的分类算法是支持向量机分类（C-SVM）[17]。本文则针对不停机间抽技术工作制度确定时出现的问题，通过对相关采油数据进行有效分析，明确影响工作制度确定因素的主次关系，并在对相关数据挖掘常用算法进行优选的基础上，构建单井个性化工作制度优化方法。

表1 生产单位制定不停机间抽工作制度（运行周期30 min）

1 常用数据挖掘方法与模型建立

机器学习数据挖掘常用的算法可分为分类、回归、聚类等，其中分类和回归是最成熟、应用最广泛的算法。对具体的研究问题、研究对象和数据源，不同的分类和回归算法具有不同的适用性。常用的回归算法包括反向传播神经网络（BPNN）、多元回归分析（MRA）和支持向量机回归（R-SVM）等，常用的分类算法包括决策树（DTR）、支持向量机分类（C-SVM）、贝叶斯判别分析（BAYD）、朴素贝叶斯（NBAY）和贝叶斯逐步判别分析（BAYSD）等[17]。由于DTR 算法建立与应用非常复杂[18]，BAYD 算法适应性弱于BAYSD 算法，因此只针对其他几类常用的数据挖掘的回归和分类算法进行不停机间抽工作制度预测，并通过对比预测过程中产生的总平均相对误差绝对值来确定最佳的数据挖掘算法。

研究结果对于低产低效井应用不停机间抽技术确定最优工作制度，从而达到节能最大化，具有较大的应用价值，也可以推广到其他数据挖掘案例，用于指导油气勘探开发、采油工作方案设计等数据挖掘工作。

1.1 模型与方法建立

检验该算法拟合度；③回归（分类）预测:将k 个预测样本代入拟合方程 y = f ( x0)，得到预测值

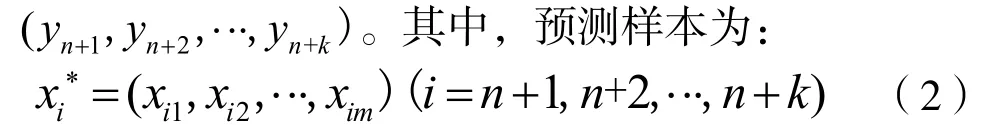
1.2 误差分析

为了表示预测样本和学习样本的预测变量y 的结果精度，通常采用相对误差绝对值Ri、平均相对误差绝对值和总平均相对误差绝对值来判断[14]。

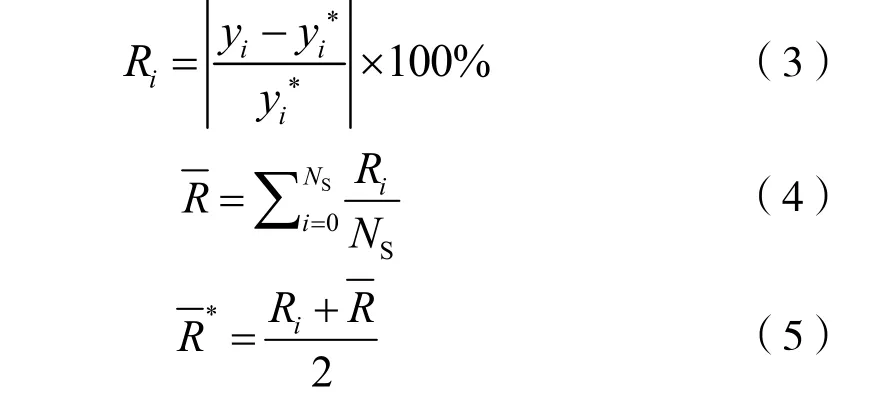
2 数据挖掘算法优选

2.1 学习样本获取

低产低效井产能的影响因素除了常规的地质特征，还应包括油压、动液面以及生产制度等多方面的因素。通过对实际油井基础数据[16]进行系统分析，将影响因素归纳为9 个独立变量（地层系数、日产液量、孔隙度、含水率、油压、冲程、冲次、泵径和泵效）。

取大庆油田A 采油厂的15 个样本数据[19-20]，其中，14 个样本作为学习样本，1 个样本作为预测样本，每个样本都有9 个独立变量数据[21]（表2），其中，因变量y*为工作制度运行时间。为了进一步准确获取15口样本井不停机间抽工作制度，对样本井进行不同不停机间抽工作制度条件下动液面恢复试验。图1 为A1 井不同不停机间抽工作制度条件下动液面恢复情况，从图中可以看出，当该井的工作制度为正常运行时间30 min，摆动运行时间30 min 时，动液面稳定在850 m 附近，可以实现油井产能最大化，所以认为该井不停机间抽最优工作制度为正常运行时间30 min，摆动运行时间30 min。按照同样方法，可以获得其他14 个样本的最优工作制度（表2）。

2.2 算法优选

2.2.1 输入参数

输入参数包括14 个学习样本和1 个预测样本的各个已知变量值 xi( i= 1,2,⋅ ⋅⋅,9)，以及14 个学习样本的预测变量y*值。另外，根据现场应用现状，一般情况下，不停机间抽运行周期可分为30，60，90，120 min，所以对于回归计算，y*值为运行时间，则摆动时间为运行周期时间减去运行时间；而对于分类计算，y*值为运行周期，表3 为不同运行周期时间对应的运行周期类别。

2.2.2 学习过程

使用回归、分类算法对表2 中14 个学习样本进行学习计算，分别建立9 个独立变量 xi( i= 1,2,⋅ ⋅⋅,9)与运行时间（回归）或运行周期（分类）的工作制度的预测拟合方程 y = f ( x0)，然后将表2 中的14 个学习样本和1 个预测样本的 xi( i= 1,2,⋅ ⋅⋅,9)值分别代入预测拟合方程 y = f ( x0)，从而得到每个学习样本的运行时间T（图2）和运行周期分类（图3），并计算每种算法所得结果的误差（表4、表5）。

表2 不停机间抽工作制度分析预测基本数据

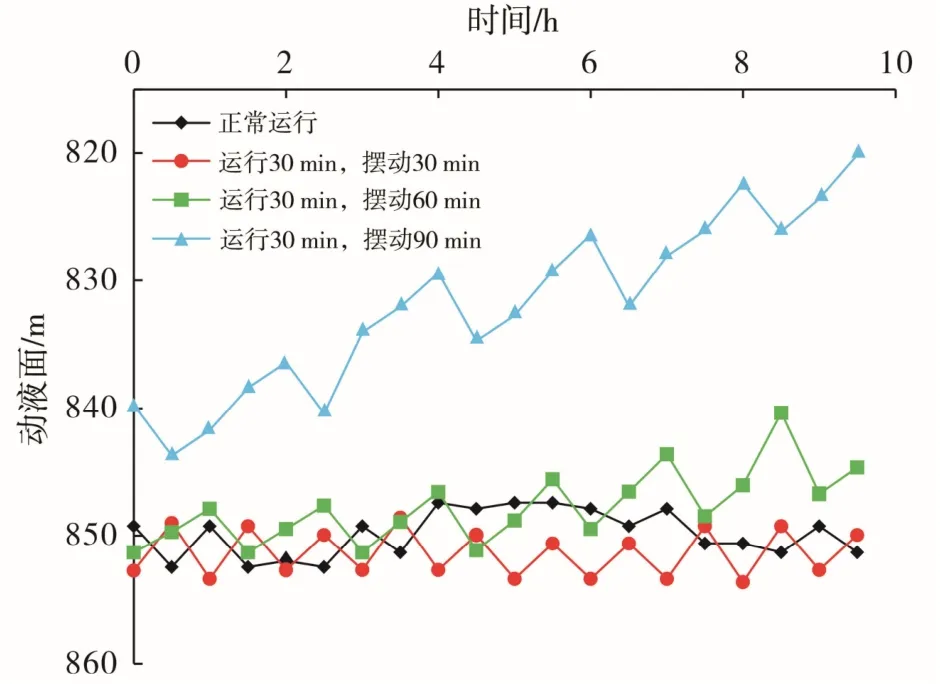
图1 A1 井不同不停机间抽工作制度条件下动液面恢复

表3 不停机间抽工作制度运行周期分类

2.2.3 回归结果分析

由图2 可知，BPNN、R-SVM 和MRA 三种回归算法最终预测的运行时间，只有BPNN 算法预测的结果与实际运行时间拟合度较高；从表4 也可以看出，用R-SVM 和MRA 算法所得的结果精度较低，而BPNN 得到的结果精度则较高。虽然不停机间抽工作制度优化过程非线性关系很强，但BPNN算法较适用。另外，MRA 算法的= 53.27%，所以预测得到的y 值与相关的9 个独立变量之间具有较强的非线性关系，MRA 算法计算出的各独立变量的相关性由大到小排序为:xi( i=5,7,6,9,8,2,1,3,4)。由于用R-SVM 和BPNN 算法所得回归方程为非线性方程，所以不能计算出预测运行时间T 与各独立变量的相关性。

2.2.4 分类结果分析

图3 为C-SVM、BAYSD 和NBAY 三种分类算法的最终预测运行周期分类，从图中可以看出，CSVM 算法结果拟合度达到100%，从表5 也可以看出，C-SVM 算法所得结果的精度非常高，Ri、和均为0，BAYSD 和NBAY 两种算法的预测精度都很低。

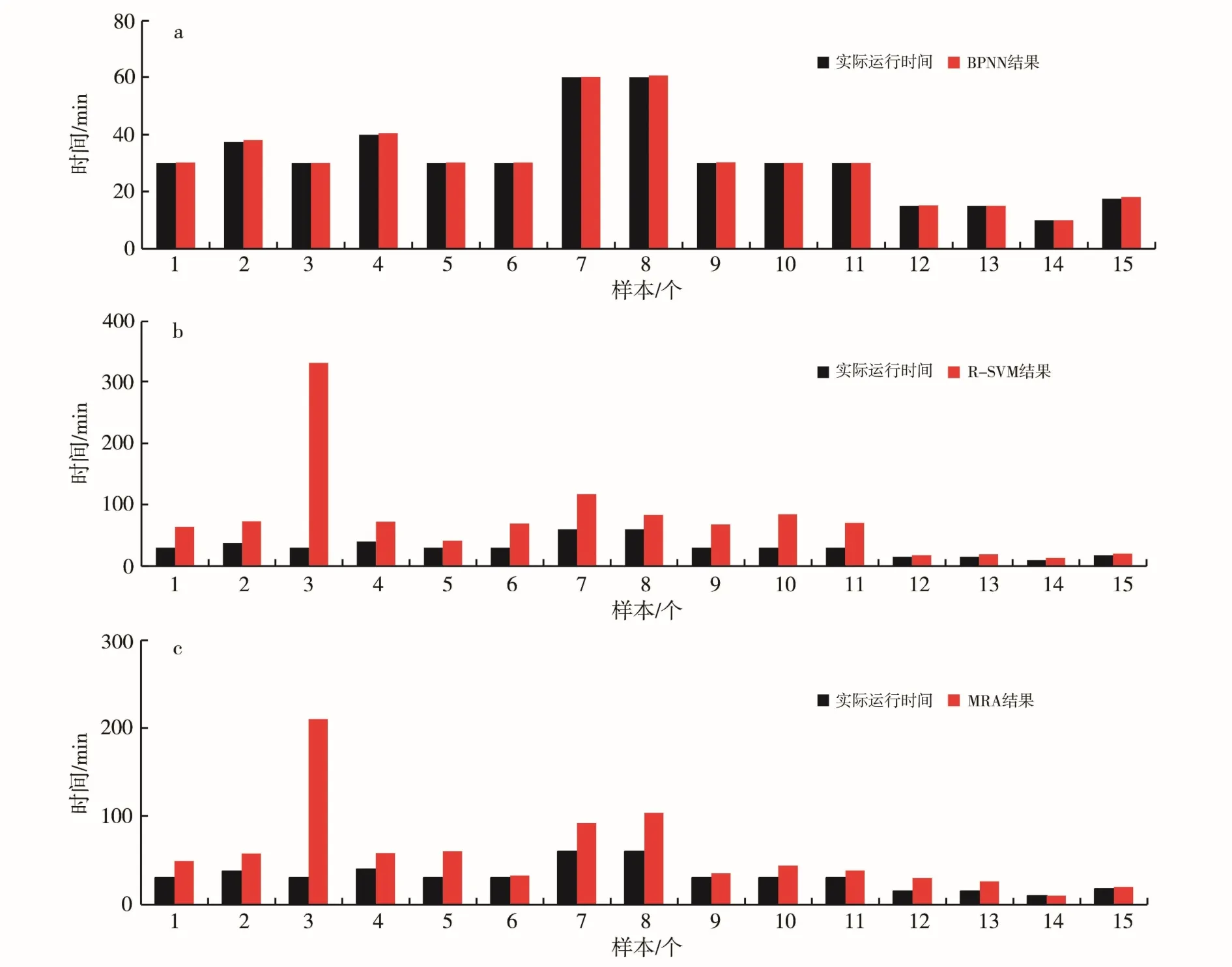
图2 不停机间抽运行时间预测结果

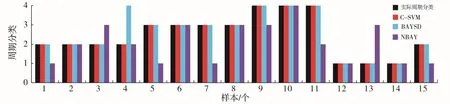
图3 不停机间抽运行周期分类结果

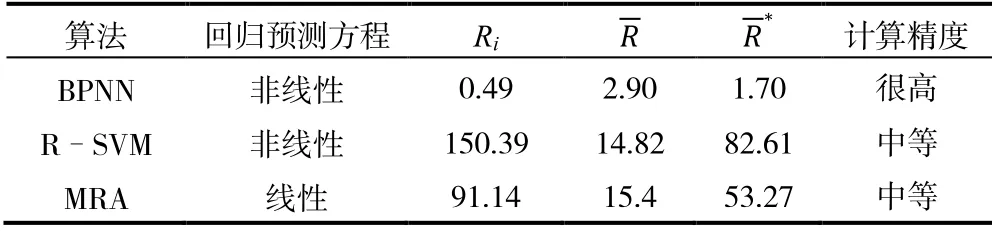
表4 三种回归算法计算不停机间抽运行时间结果误差 %

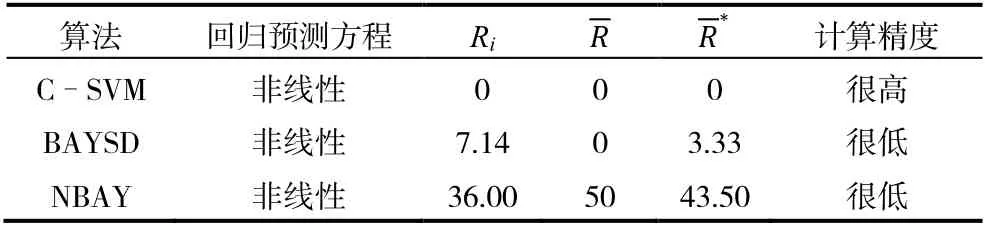
表5 三种分类算法计算不停机间抽运行时间结果误差 %

综合数据挖掘的回归和分类算法，优选得到C-SVM—BPNN 算法。

3 C-SVM—BPNN 应用实例分析

通过C-SVM—BPNN 算法对A 采油厂所应用的不停机间抽技术进行工作制度优化，由表6 可知，在产液量变化不大的情况下，优化后泵效提高2%～8%，系统效率提高3%～5%。

4 结论

（1）常用数据挖掘算法用于优化不停机间抽工作制度，最优的回归算法是BPNN，其次是MRA 和R-SVM；最优的分类算法是C-SVM，其次为NBAY和BAYSD。机器学习数据挖掘应用研究过程中，对于具体的研究对象、研究问题和数据源，不同的回归和分类算法具有不同的适用性，所以针对不同问题要进行算法的优化选择。

（2）利用C-SVM—BPNN 算法对不停机间抽工作制度进行优化的实例表明，优化后的不停机间抽井系统效率和泵效均有明显的提升，说明CSVM—BPNN 算法具有较好的应用效果。

表6 部分井不停机间抽工作制度优化前后运行情况对比