算术计算Petri网模型及实现

摘 要：为便捷证明算术计算Petri网模型的计算能力，分析其具体计算过程.结合面向对象编程语言Java开发插件Arithmetic Petri Net Simulation（APNS），对网中的库所、变迁、弧元素进行实例化，重写Fire方法生成自定义格式的模型运行日志;利用轻量级控件Swing实现交互界面，在模拟运行时对可触发变迁的发生进行选择，利于模型计算过程是否唯一的分析;提出（A+B）*（C-D）与A*B-C*D两个计算模型.实验对幂次方运算、（A+B）*（A-B）以及A^2-B^2模型进行模拟，对插件的可交互性、模型的可行性、幂次方模型运算过程的唯一性以及（A+B）*（A-B）与A^2-B^2模型的等价进行了分析与证明.

关键词：算术计算Petri网;面向对象;Java;Swing;日志

中图分类号：TP391.9  文献标识码：A  文章编号：1673-260X（2020）08-0021-04

0 引言

算术运算Petri网是带抑制弧的増广Petri网的一类模型举例，通过对带抑制弧的Petri网模型的理解辅助解决实际建模中的问题[1，2].文献[3]提出了一个增广Petri网模型实现乘法运算和除法运算;文献[4]提出了一个增广Petri网模型模拟乘方和开方运算的方法;以上运算模型均从理论方面证明了模型的可行性.在计算机高速发展的今天，通过编程可以辅助科研人员进行许多数据的处理与可视化、算法的证明等繁杂工作.文献[5]利用Cpntools及分析代码对SAMG问题的验证进行辅助及补充，弥补人类专业知识对SAMG工作流程验证的不足;文献[6]使用PIPE对具有多个控制器攻击的SDN问题进行建模，以分析攻击者的不确定性;文献[7]使用Tina对具有时间因素的无线传感器网络丢包问题进行建模，并分析模型的有界性、可逆性等，以证明协议的正确性;以上工具均为科研工作提供了很多便捷之处以及助力，但验证的模型结构是静态的.综上所述，由于计算模型大多仅有理论证明，且如幂次方计算模型的动态性，一般仿真软件不可对其证明.文章在此开发出一个对算术计算Petri网模型的正确性、可行性进行编程化验证分析的插件.

1 算数计算的增广Petri网模型

本节首先展示幂次方运算的Petri网模型[4]，随后基于对网模型的理解提出计算模型（A+B）*（C-D）与A*B-C*D.出于篇幅限制，本文密切相关的Petri网知识见文献[2].

1.1 幂次方运算Petri网模型

正此小节给出了计算xm的増广Petri网模型如图1所示，主要思路是xm=x*x*x*…*x，将多个乘法运算模型通过变迁t4n+i和库所P5n+1+i（i=1，2，3…m-1）进行关联，其中t4n+i相关联的抑制弧保证了完成当前乘法运算模型的运行后在继续下一个乘法模型的计算;通过P6n+2输入幂次方运算的底数x，限制第一个x2的计算;并利用t5n，对每个乘法模型输入乘数x;最后使用P6n+1中m-2个Token个数限制乘法模型的关联个数为m-1，自此完成计算xm的増广Petri网模型，其中P5n+1输出计算结果.

1.2 复合算术运算Petri网模型

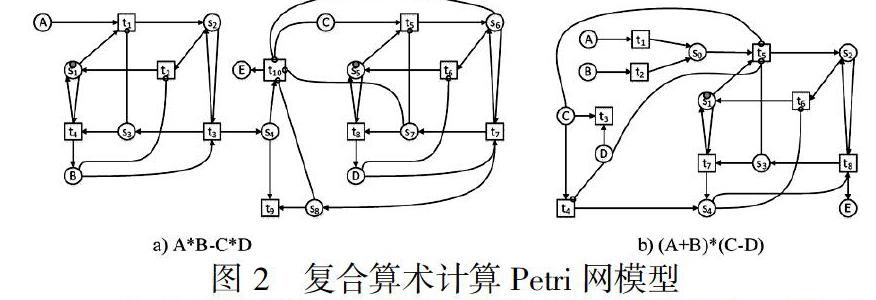
此小节给出了计算A*B-C*D=E与（A+B）*（C-D）=E的増广Petri网模型如图2所示，主要思路利用加减法模型与乘法模型[8]的复合生成新的计算模型，通过抑制弧的加入限制复合后模型的分块执行顺序.

通过乘法模型实现A*B与C*D的计算，用减法模型对乘法模型模型连接，加入抑制弧（C，t10）， （s6，t10），（s7，t10）生成A*B-C*D算术计算模型.抑制弧的加入是为了确保C*D计算在s4-s8的运算开始之前完成，避免抑制弧（s8，t10）因减数的缺失而失去应有抑制效果，导致复合模型中减法运算结果异常.

通过加法模型与减法模型实现（A+B）、（C-D）的运算，再利用乘法模型对加减法模型连接，加入抑制弧（C，t5），（D，t5）生成最终的（A+B）*（C-D）算术计算模型.抑制弧的加入是为了（C-D）的计算在t5触发之前完成，避免因乘数的异常，导致复合模型中乘法运算结果异常.

2 APNS插件的开发以及计算模型的分析

2.1 APNS插件的开发以及计算模型的分析

在此利用Java编码实现带抑制弧的増广Petri网的运行逻辑，Eclipse插件WindowBuilder实现可交互图形界面.利用面向对象的思想，创建Arc.java，InhibitorArc.java，Petrinet.java，Petrinet-Obj.java，Place.java，Transition.java共六個类，对库所、变迁、流弧、抑制弧和网结构进行实例化，且对变迁是否可触发及触发规则进行了代码化（类图如图3所示）;并在主界面定义多个触发事件，利用java.io.File包实现变迁触发日志的导出;创建Operation.java将算术运算Petri网的模型代码抽象化;创建Gui_Main.java和PetrinetGUI.java利用WindowBuilder Editor实现插件主控、交互以及文件导出界面如图4所示.

交互界面可以观察可触发变迁，通过点击进行触发，并在主界面生成对应触发记录;同样可以点击autoRun按钮，对Petri网中的变迁进行遍历，对当前可触发变迁利用ArrayList进行缓存，然后随机触发，直到当前无变迁可触发即停止运行.对应代码如Code-1：

从插件大小、模型设定、交互运行、日志导出共4个方面，用此插件与PIPE、CPNTools、Tina3个Petri网仿真软件进行对比，结果如表1所示.插件APNS在实现算术Petri网模型仿真方面，具有体积小、可交互以及自定义日志导出的优势.由于幂次方计算模型的动态性，将在2.2节详细介绍其模型构建方式.

2.2 幂次方运算的实现

此小节介绍了将xm对应算术运算Petri网模型输入至插件的过程.在此増广Petri中，当网处于初始状态M0时，库所P6n+2输入x个Token用作乘法结构的乘数、库所P6n+1输入m-2个Token用作限制乘法结构个数为m-1.此时可计算出图中变迁总数为5*（m-1）、库所总数为6*（m-1）+2.

对于图1中流弧个数可分为9个部分来求取：顶部P6n+1直接关联的所有流弧共（m-1）条;乘法増广Petri网结构内的所有流弧共15*（m-1）条;底部输入弧，t5n的所有输出弧共m条;顶部关联抑制弧乘法结构抑制t4n+h的3条抑制弧共3*（m-2）条;连接乘法结构的流弧共2*（m-2）条;顶部输入弧，对t4n+h输入的流弧共（m-2）条;顶部输出流弧共（m-3）条;初始化弧共3条;输出流弧共1条，库所与变迁之前的关系弧共24*m-28条.

对于模型的输入代码，首先初始化库所集、变迁集以及弧集，其中重要的部分为弧集的初始化问题，部分代码如Code-2：

3 实验部分

本节对（A+B）*（A-B）、A^2-B^2以及xm三个计算模型进行模拟运行，通过调整输入参数获得不同计算结果，以及输出日志.所有的测试均在配有I5-7300HQ 2.5Ghz四核处理器和16GB运存的机器上进行的，使用的Java SE 1.7开发环境.

首先就模型执行过程的唯一性，由于存在加、减法运算的复合，假设（A+B）*（A-B）与A^2-B^2运算过程不为一.设A=3，B=2.（A+B）*（A-B）模拟运行两次获得两条长度为28的变迁触发日志：

L1=（t2，t1，t1，t2，t1，t3，t3，t4，t5，t8，t6，t7，t5，t8，t6，t7，t5，t8，t6，t7，t5，t8，t6，t7，t5，t8，t6，t7）

L2=（t1，t3，t3，t4，t2，t5，t1，t1，t2，t8，t6，t7，t5，t8，t6，t7，t5，t8，t6，t7，t5，t8，t6，t7，t5，t8，t6，t7）

A^2-B^2模拟运行两次获得长度为45的变迁触发日志：

L3=（t5，t1，t3，t7，t7，t3，t3，t2，t9，t9，t6，t8，t4，t4，t8，t5，t4，t1，t3，t7，t3，t7，t3，t2，t4，t9，t6，t8，t9，t8，t4，t4，t1，t10，t10，t3，t10，t3，t10，t3，t10，t2，t4，t4，t4）;

L4=（t1，t3，t5，t3，t7，t3，t7，t6，t8，t2，t4，t9，t9，t4，t4，t1，t3，t3，t8，t3，t5，t2，t7，t9，t4，t4，t4，t7，t6，t9，t8，t1，t8，t10，t10，t3，t10，t3，t3，t10，t2，t4，t4，t4，t10）;

其次取A=i+1，B=i（其中i=1，2，3，4，5，6），两个计算模型均能正确计算出结果且模型结构不随参数变化，但执行效率随着i的增大差异愈发明显，如图5所示.

取底数为x（x=2，3，4），次数为i（i=3，4，5，6，7），对应计算的流程有且唯一，幂次方计算模型复杂度（变迁个数如图6a所示），以及对应变迁触发次数如图6b所示所示.随着次数i的的增加，模型中变迁个数呈线性增加;随着次数或底数的增加，模型计算变迁触发次数呈指数增长如图6c所示.

4 总结

文章通过带抑制弧Petri网的强模拟能力引出算术计算Petri网模型的构建.使用Java语言开发出插件APNS模拟带抑制弧Petri网的运行，且可导出变迁触发日志用以分析运行过程;通过对现有网模型的复合，提出平方差公式的计算模型;将模型嵌入APNS中，模拟计算证明模型的正确性，导出变迁触发日志分析随自变量i的增加A^2-B^2计算效率高于（A+B）*（A-B）;幂次方运算过程有且唯一，随次数i的增加模型中变迁数量线性增加，变迁触发次数呈指数增长.

已开发的插件APNS可有效模拟带抑制弧Petri网的运行，但模型的代码化输入不够常规.在未来的工作中主要是利用复合网模型的方法生成更多常用模型嵌入插件中并验证，以及增加界面化的模型输入.

参考文献：

〔1〕吴哲辉.Petri网导论[M].北京：机械工业出版社，2006.

〔2〕邵叱风.基于流程挖掘的并行优化算法[J].赤峰学院学报（自然科学版），2019，35（10）：66-70.

〔3〕吴哲辉.实现乘法计算的增广Petri网模型[J].山东矿业学院学报，1986，96（02）：12-16.

〔4〕许安国.实现自然数m次乘方和开m次方的增广Petri网模型[J].山东矿業学院学报，2017，34（04）：81-89.

〔5〕Lee Y S， No Y G， Seong P H. Validation of severe accident management guidelines （SAMGs） for advanced power reactor 1400 （APR1400） using colored Petri net （CPN） Tools[J]. Annals of Nuclear Energy， 2019， 126： 186-193.

〔6〕Almutairi L， Hong L， Shetty S. Security analysis of multiple SDN controllers based on stochastic Petri nets[C]//2019 Spring Simulation Conference （SpringSim）. IEEE， 2019： 1-12.

〔7〕Louazani A， Sekhri L. Time Petri Nets based model for CL-MAC protocol with packet loss[J]. Journal of King Saud University-Computer and Information Sciences， 2019.