基于应力传递系数的分析模型优化与土壤压实应力预测

贺亭峰 丁启朔 张 伟 姜春霞 刘恩科

(1.山西农业大学山西有机旱作农业研究院， 太原 030000； 2.有机旱作山西省重点实验室， 太原 030000；3.南京农业大学工学院， 南京 210031； 4.黄土高原东部旱作节水技术国家地方联合工程实验室， 太原 030000)

0 引言

田间行走机械不可避免地造成了土壤压实[1-3]，而土壤应力是压实过程中导致土壤结构及其功能失效的主要原因[4-8]。因此，对土壤应力传递过程的定量描述是科学控制机械压实的重要前提。分析模型与仿真模型是研究土壤应力最常用的方法[9-11]。

与仿真法建立的土壤模型相比[12-15]，土壤压实分析模型在使用时因所需参数少、操作简单而被广泛运用[16-21]。该模型基于BOUSSINESQ方程，经集中系数修正后[22-23]，假设土壤在受压过程中表现为弹塑性变形，模型准确预测土壤应力的关键是选择合适的集中系数[24-25]。HORN等[26]与SMITH等[25]的研究表明，集中系数是关于轮胎-土壤接触面当量半径、土壤厚度、接触面表面应力与土壤应力的函数，通过实测表面应力σ0与土壤应力σz可对该参数随加载和土壤环境的变化规律进行研究[25-27]。SÖHNE[23]研究发现，集中系数随含水率的增大而增大，提出土壤在坚硬、中度、松软3种条件下分别取值为4、5、6。HORN等[26]试验表明，集中系数与先期固结压力相关，集中系数取值范围为6～9，且与轮胎-土壤接触面当量半径间呈负相关变化趋势。RAM[28]利用重塑土试验控制土壤含水率和容重，探究集中系数的影响因素，发现容重从1.24 g/cm3变化到1.63 g/cm3的过程中，对应的集中系数从5.4减小到1.5。在其他同类型的研究中[27,29-31]，集中系数取值范围是2.0～14.3。

鉴于集中系数取值的不一致性，HE等[24]通过定义表征应力在土壤中传递效率的无量纲参数——应力传递系数(Stress transmission coefficient，STC)，研究了土壤环境因素对集中系数的影响。贺亭峰等[32]基于30种状态的重塑土壤试验发现，应力传递系数随土壤含水率的增大而增大，与土壤初始干密度、先期固结压力之间呈明显的负相关性，即高含水率的土壤条件更有利于应力往土壤底层传递，初始干密度与先期固结压力较大的土壤不易被压实，故而明确了土壤环境因素对集中系数的影响。

集中系数受土壤环境和加载环境双重影响[33]，系统定量加载环境(轮胎-土壤接触面当量半径、土壤厚度)对集中系数的影响未知。轮胎-土壤接触面面积受轮胎尺寸、胎压及轴重等加载环境因素的直接影响[25-27]，轮胎-土壤接触面当量半径即代表加载环境对集中系数的影响。从严格意义上讲，土层厚度并不属于加载环境，仅作为影响集中系数的一个重要参数[32]，其变化必然引起土壤应力传递过程的改变。然而，基于有限尺度环刀(Φ50×50 mm)的土壤应力传递系数取值方法[24,32]无法满足不同深度土壤条件下集中系数随加载环境变化的研究。

本文对分析模型及应力传递系数进行研究，推导ΠSTC公式，以多层土壤应力传递系数连乘方式实现田间指定厚度土壤应力传递系数的计算；同时，基于土压力传感器技术进行田间原位试验和室内非扰动土试验，以期验证田间土壤应力传递系数是否稳定可测，分析应力传递系数与加载环境因素间的相关性，评价ΠSTC公式的可靠性，研究集中系数随加载环境的变化规律。

1 理论分析

使用分析模型预测土壤应力，假设加载力均匀地分布在当量半径为R的圆形接触面，此时接触面正下方z处垂直方向的应力可表示为

(1)

其中

σ0=W/(2πR2)

式中σ0——轮胎-土壤接触面表面应力，kPa

W——轮胎-土壤接触面范围内的总载荷，kg

σz——轮胎-土壤接触面正下方z位置处垂直方向的应力，kPa

ν——集中系数

HE等[24]通过公式推导，将集中系数转换为关于应力传递系数、土壤-轮胎接触面当量半径、轮胎-土壤接触面与正下方应力预测点间的垂直距离的函数，由此定量了集中系数随土壤环境的变化规律

(2)

其中

S=σz/σ0

式中S——土壤应力传递系数

本研究按照TRAUTNER[20]的方法，在固定的土壤环境中，将土壤剖面进行分割，如图1所示，各土层厚度分别为z1，z2，…，zn，假设应力在向下传递过程中每一土层垂直向下的土壤应力均匀分布，且把任一土层下表面的土壤应力作为模型输入，计算下一土层的土壤应力，同时假设理想状态下轮胎-土壤接触面形状为圆形。因此，在载荷为W，半径为R0的圆形压板作用下，压板-土壤接触面应力为σ0，各土层下表面垂直方向的应力分别为σ1，σ2，…，σn(kPa)，相应的应力传递系数分别为S1，S2，…，Sn。

图1 田间原位土壤应力传递系数计算原理图Fig.1 Diagram of field in-situ stress transmission coefficient calculation

因此，各土层下表面的土壤应力可表示为

(3)

式中σi——第i层土层上表面应力

Ri——第i层土层上表面压实应力σi分布区域的当量半径,m

zi+1——第i+1层土层的厚度

νi+1——第i+1层土层对应的集中系数

按照TRAUTNER[20]的方法，第n层的土壤应力可表示为

(4)

简化后为

(5)

式中Ssum——整个土层的应力传递系数

Ssum是关于Ri、zi+1和νi+1的函数，应力在土壤中传递时，除zi+1是可测常数，Ri和νi+1均随土层深度发生变化[19]，可知各土层的应力传递系数为

(6)

式中Si——第i层土层的应力传递系数

根据文献[24]研究，假设各土层的应力传递系数S1，S2，…，Sn的数值可通过田间分层取样并结合室内单轴压缩试验测量，将所得数值代入式(5)可得

(7)

通过推导，指定厚度土壤的应力传递系数取值转换为对分割后各土层应力传递系数的测量。这种通过多层土壤应力传递系数连乘方式求解田间土壤应力传递系数的公式称为ΠSTC公式。

2 材料与方法

上述理论假设轮胎-土壤接触面形状为圆形，本试验选择不同尺度的圆形压板，基于土压力传感器技术，分别进行田间原位和室内非扰动土试验，土压力传感器被用于量化土壤内部应力和表面应力间的关系[11,16,25,29-31,34-35]。

2.1 田间原位试验

试验地点位于南京市六合区八百桥农场(118°93′E，32°42′N)，农场为长期稻麦轮作区，试验时间2018年11月，试验地土壤为粘性水稻土，土壤液限47%，塑限26%，砂粒、壤粒、粘粒和有机质质量分数分别为22%、39%、38%和0.32%。试验时选择一块未被扰动的地块，采用张维强等[36]的方法，测量该地块的贯入阻力，结果如表1所示(表中同列数据不同字母表示数据差异显著)；参照柏建彩等[35]的研究，以倾斜角30°钻孔方法将土压力传感器(Φ17×7 mm，量程1 MPa)埋设于指定土壤深度的土层(土壤深度100、150、200 mm)，使用标准沙回填孔洞，如图2a所示；搭建台架如图2b所示，通过勾股定理定位加载位置；选用不同直径的压板(压板直径80、100、150 mm)开始加载，并通过测控系统记录加载载荷信号及随之变化的土压力传感器应力信号，同时记录压板相应的下陷位移ε。为防止相邻加载点之间的应力干扰，加载位置间隔不小于1 m，每组参数试验重复3次。

图2 田间原位测控系统Fig.2 In situ instrumentation system1.压板 2.标准砂 3.土压力传感器 4.导轨 5.配重块 6.龙门导向 7.液压缸 8.台架 9.电缆 10.测控系统 11.压板导向装置 12.称量传感器 13.位移传感器

区别于传统通过土壤剖面并水平钻孔放置传感器的操作，本研究采用的土压力传感器埋设的方式省时省力，在保证土压力传感器安放深度的同时，最大限度减少原位土壤的扰动[37-38]，经研究[38-39]此方法亦可达到预期测试效果，尤其能够满足短时间内进行多点测量的要求。

2.2 室内非扰动土试验

在进行田间原位试验的同时，于每个加载位置附近选择一块较为平整的未扰动区域，清茬后，使用内壁抹上一层凡士林的环刀(Φ50×50 mm)[40]，按如图3a所示方法进行取样，密封并贴好标签后继续取样至深度200 mm。土样带回实验室并按照HE等[24]的操作，使用土壤固结仪对土壤样品进行加载，同时运用土压力传感器监测因逐次加载(σ0)而变化的土壤应力(σz)(图3b)，同时记录加载板下陷位移ε(mm)[41]，进而获取各土层土壤的应力传递系数，测量得土壤含水率、容重如表1所示。

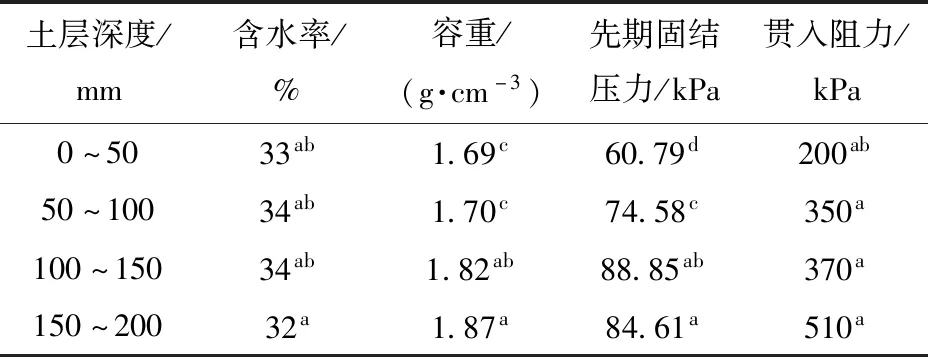
表1 田间土壤物理参数Tab.1 Soil physical parameters in field

图3 有限尺度取样与固结仪试验Fig.3 Sampled in finite-size and oedometer test1.土壤样品 2.标尺 3.固结仪 4.土压力传感器 5.测控系统

2.3 数据分析

标定称量传感器、位移传感器与土压力传感器[40]。根据CASSAGTANDE方法[41]计算各参数土壤样品的先期固结压力，结果见表1。采用HE等[24]的方法通过建立土壤应力-表面应力线性关系，获取田间不同厚度土壤的应力传递系数和室内非扰动土各土层(0～50 mm、50～100 mm、100～150 mm、150～200 mm)的土壤应力传递系数[24]。基于室内非扰动土壤试验结果，运用ΠSTC公式计算不同厚度土壤的应力传递系数。利用SPSS-Statistics 20.0统计软件[24]进行双因素(压板尺度、土层厚度)方差分析，采用DUNCAN方法进行多重比较(α=0.05)。

运用ΠSTC公式，首先获得土壤剖面各土层的应力传递系数，采用连乘的方式计算不同厚度土壤应力传递系数。

3 结果与分析

3.1 田间土壤应力传递系数

图4为田间原位土壤与室内非扰动土壤在承压过程中，土壤应力随压板-土壤接触面表面应力变化曲线。由图4可知，表面应力与土壤应力间线性关系显著，与贺亭峰等[32]的重塑土试验结果相同。因此，田间原位土壤和室内非扰动土壤均存在与重塑土同样的属性，即对于给定的土壤，在其一次性加载过程中，应力传递系数(σz/σ0)始终保持恒定，且数值等于σz-σ0拟合曲线的斜率。由此获得各土层(0～50 mm、50～100 mm、100～150 mm、150～200 mm)的土壤应力传递系数均值分别为0.63、0.48、0.55、0.44。应力传递系数为表征土壤自身应力传递性能的独立物理参数，其受土壤特性的综合影响，结合表1可得各土层土壤含水率并无显著性差异，相应应力传递系数的变化规律亦不明显，而随着容重和先期固结压力的增大，应力传递系数基本呈减小趋势，与贺亭峰等[32]的试验结果一致。

图4 一次加载过程中压板-土壤接触应力与土壤应力关系Fig.4 Relationships between soil stress σz and surface stress σ0 in a loading process

3.2 加载环境对应力传递系数的影响

基于ΠSTC公式计算得3种厚度(100、150、200 mm)土壤应力传递系数分别为0.30、0.17、0.07，如图5所示，随着压板直径的改变，实测与计算所得同等厚度土壤的应力传递系数间并无显著差异，表明对于给定的土壤，其应力传递系数并不受测量试验中压板直径的影响，可以忽略压板直径对测量结果的影响，也意味着运用ΠSTC公式计算田间土壤应力传递系数方法可行；同时验证了应力传递系数是与土壤综合特性相关的独立物理参数，其取值不受外界环境的影响[24]。由于应力传递系数是小于1的无量纲参数[32]，根据ΠSTC公式推断，随着土层厚度的增加，应力传递系数呈下降趋势，田间试验结果表明，随着土层厚度的增加，应力传递系数均随之减小，即土壤的应力传递性能随土层厚度增加而减弱，与基于公式的推断完全一致。

图5 压板直径、土层厚度对应力传递系数的影响Fig.5 Effect of plate diameter and soil thickness on STCs

3.3 ΠSTC公式计算土壤集中系数

文献[26-27,32]研究表明，集中系数受加载环境和土壤环境的双重影响，是关于应力传递系数、轮胎-土壤接触面当量半径和土层厚度的函数，通过计算所得不同加载环境(压板直径、土层厚度)中田间原位土壤集中系数如表2所示。由表2可得，随着土层厚度的增加，集中系数总体呈下降趋势，且随压板直径的增加而减小，这与HORN等[26]给出的结果一致。区别于传统基于土壤硬度的集中系数取值方法，ΠSTC公式通过应力传递系数直接与加载环境参数建立关系。同样硬度的土壤，不同轮胎-土壤接触面当量半径R、土层厚度z，集中系数间存在较大差别。为了简化分析模型研究，采用圆形压板代替轮胎进行试验。

表2 基于应力传递系数计算的集中系数Tab.2 Calculated concentration factors from STC

3.4 模型预测土壤应力分析

由表2可知，压板直径R=100 mm，土层厚度z=200 mm时集中系数为2.38。图6为压板直径100 mm，加载面正下方土层深度200 mm处垂直方向土壤应力的实测值与预测值的变化曲线。由图6可知，3次重复试验中，土壤应力的预测和实测值变化趋势基本一致，随着加载力的增大而逐渐升高。如图6a所示，压板下陷使表面应力达到峰值137.0 kPa，此时土壤应力预测值和实测值分别为19.0、16.0 kPa。如图6b所示，预测曲线和实测曲线重合度较高，当压板分别下陷至10、20、30、40 mm位置时，实测土壤应力为3.5、7.0、12.0、16.0 kPa，而相应预测值为4.0、7.5、13.6、14.0 kPa。如图6c两条曲线几乎重合，当表面应力最大为103 kPa时，土壤应力的预测和实测值分别为13、17 kPa。所有的实测土壤应力均在预测值上下浮动变化。由于试验期内雨水过多，田间土壤平均含水率较高(表1)，土壤极易被压实，3次重复中，当下陷位移达40 mm时，加载力刚超过100 kPa。

图6 压实过程中土壤压实应力的实测值与预测值Fig.6 Measured and predicted stress state during soil compaction process

4 讨论

压实会影响土壤自身的物理、化学、生物特性，进而产生诸多农艺问题(如限制根系生长、作物减产等)和环境问题(侵蚀、养分丢失等)[27]。利用模型研究土壤压实过程可分为3个阶段[27, 32]：表面应力分布模型描述轮胎-土壤接触面应力分布；分析模型定量土壤应力；土壤失效模型研究应力引起土壤结构的变化。模型通过分析土壤应力传递等压实过程，为科学控制机械压实提供了可视化的数据。经FRÖHLICH等[22]和SÖHNE[23]修正后，分析模型广泛地应用于土壤机械压实领域，然而传统的集中系数取值方法限制了该模型的准确性。由于对加载环境与土壤环境等因素影响土壤应力传递过程认识的不足[24,27]，尽管基于田间实测的轮胎-土壤接触面表面应力与土壤应力的集中系数研究众多，分析模型预测土壤应力的准确性仍受制于集中系数取值[24]。本文基于ΠSTC公式，建立加载环境与集中系数关系的基础上，提供了集中系数取值的方法，并较为准确地预测了压实过程中的土壤应力变化，为下阶段开展土壤应力引起土壤形变的力学过程研究提供了技术基础。

5 结论

(1)在田间原位土壤条件下，应力传递系数仍稳定可测，其数值等于压板-土壤接触面表面应力σz与土壤应力σ0拟合曲线的斜率，且应力传递系数与压板-土壤接触面当量半径无关，并随土层厚度的增加而减小。

(2)基于分析模型推导了ΠSTC公式，以多层土壤应力传递系数连乘方式求解田间土壤应力传递系数，验证了田间原位不同深度土壤应力传递系数计算的可行性。

(3)集中系数受轮胎-土壤接触面当量半径与土层厚度的综合影响，可由应力传递系数计算获取。

(4)基于ΠSTC公式，分析模型较为准确地预测了压实过程中的土壤应力变化。