基于离散元的稻板田旋耕功耗预测模型研究

祝英豪 夏俊芳 曾 荣 郑 侃 杜 俊 刘政源

(1.华中农业大学工学院， 武汉 430070； 2.农业农村部长江中下游农业装备重点实验室， 武汉 430070)

0 引言

长江中下游多熟制稻作区主要实施稻油、稻麦水旱轮作种植模式。稻板田栽播冬油菜、冬小麦前的耕整不同于北方的以松代犁，水旱轮作制的土壤耕整不仅需要符合旱作物栽培根系生长环境要求，同时也应避免犁底层过度破坏导致蓄水困难，影响下茬水稻种植。由于北方模式不适用，为解决南方稻板田土壤粘结严重、茬口农时矛盾、前茬稻秆量大株高等耕作难点，以旋代犁的土壤旋耕秸秆旋埋技术及装备为其提供了新的解决方案[1-2]。其核心部件旋埋刀辊通过在传统旋耕刀辊内加装切幅较宽的螺旋横刀，起到防缠绕、秸秆旋埋以及提升碎土率的作用，但由此导致的高功耗问题尤为突出。因此研究旋埋刀辊的减阻降耗对于稻板田耕整及后续油麦栽培具有重要应用价值[3]。由于旋埋刀辊结构复杂、各因素存在交互作用、优化项目主次不明确、刀辊试制成本高，以及稻板田耕作时节限制等因素影响，仅通过田间试验途径研究刀辊减阻降耗比较困难，所以研究初期亟需构建稻板田旋耕功耗预测模型，以指导刀辊优化设计。

离散元法(Discrete element method，DEM)是一种用于分析与求解复杂离散系统动力学问题的数值方法，广泛应用于散粒结构的模拟研究[4-5]。土壤是农业工程领域中最常见的颗粒状物料之一，普遍存在的各向异性、非均匀及不连续等特征使土壤耕作系统更加复杂[6]。离散元法能有效解决耕作部件与土壤相互作用的非线性问题，获取田间试验无法测量的数据信息，对耕作部件的性能进行预测及参数优化，是当前农机具研究的重要辅助手段。国内外学者基于离散元耕作模型开展了大量研究，主要涉及耕后力学指标评估和土壤形态及细观位移分析，其中深松铲与土壤的接触模型相对成熟，土壤无滑移摩擦接触模型[7]、延迟弹性接触模型[8-9]和粘结接触模型[10-12]应用广泛。为增加深松行为的模拟精度，根茬[13]以及土层差异情况[14-15]也被考虑在模型构建中。深松为土壤小扰动耕作行为，其耕作模型不适用于旋耕。而针对旋耕作业的离散元模型研究报道较少，根据文献[16-17]，目前模型应用局限于单回转面旋耕(1～3把旋耕刀)及土槽试验，无法推演旋耕刀辊的田间真实作业情况。

本文根据稻板田土壤性质及旋埋刀辊旋耕作业特点，构建刀辊-土壤相互作用模型，旨在预估旋埋刀辊作业功耗，为后续旋埋刀辊减阻降耗的优化设计提供理论依据，同时获取的功耗数据可为刀辊扭力分析提供参考。

1 稻板田旋耕模型构建

土壤接触模型通过微观层面描述土壤颗粒间的动力学行为以表达宏观土壤在载荷下复杂的应力应变特性。农具作用于土壤，土壤不断形变直至破坏失效，同时土壤将产生的反作用力以耕作阻力的形式反馈给农具。耕作过程由土壤和农具共同参与，因此为确保仿真正确度，构建离散元模型时在考虑土壤性质的同时也需要关注农具结构及耕作方式的特殊性。

1.1 土壤颗粒接触模型选取

长江中下游稻作区土壤普遍为粘性质地，稻油、稻麦水旱轮作导致土壤常年干湿交替，对于粘土而言，土壤性质受含水率影响较大。在工程应用中，粘土因含水率表现出的软硬稀稠程度通常由液塑限指标衡量，该指标将土壤分为固态、塑态和液态[18]。土壤的固塑液状态关系到耕作时土壤破坏形式，固态土壤强度大，受载后易产生裂纹并扩散破碎；塑态土壤可塑性强，能承受较大塑性形变而不离散；液态土壤呈泥浆状，几乎不具备抵抗外力和维持原有形状的能力。在夏秋水稻收获季节，由于气候和地表裸露等因素，土壤含水率处于一年中最低水平，此时粘土湿胀干缩特性导致的田面土壤裂缝是稻板田最显著的特征。根据2017年至2019年在华中农业大学现代农业科技试验基地中稻收获后所得试验检测结果显示，稻板田耕层土壤含水率在20.38%～28.24%之间。为进一步评估稻板田土壤破坏特征，使用五点法取田间土壤，利用LP-100D型数显式土壤液塑限联合测定仪(上海路达实验仪器有限公司)，依据SL 237—1999《土工试验规程》要求，对土壤塑限进行测量，结果如图1所示，其中塑限均值为24.45%，液限均值为43.28%。

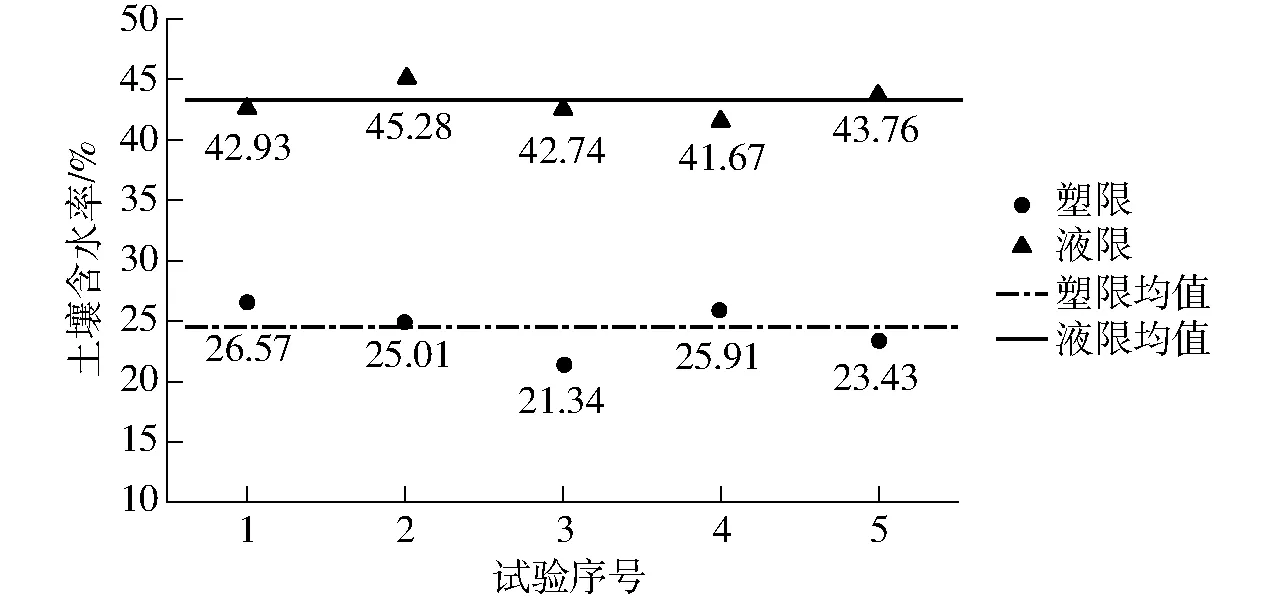
图1 液塑限试验结果Fig.1 Result of liquid plastic limit test

由图1可知，稻板田含水率区间(20.38%～28.24%)与塑限区间(21.34%～26.57%)十分接近，与液限区间(41.67%～45.28%)差距明显，此时土壤仅可承受较小的形变并很快破碎，因此在进行离散元建模时可将稻板田土壤作固态处理。

HertzMindlin with Bonding颗粒接触模型[19]能够同时反映土壤的不连续性与团聚特点，有效解决农具与土壤相互作用的非线性问题，该模型不仅继承了HertzMindlin(no slip)的算法，而且通过在土壤颗粒间设置粘结键的方式，添加额外的力与力矩以约束颗粒运动，粘结键受载断裂后，不能再次生成，符合稻板田土壤破碎后保持松散状态的力学行为特征。该模型共有5个参数，其中法向、切向刚度以单位步长为间隔不断迭代并更新粘结键所受的载荷(力与力矩)；法向、切向临界应力为判断粘结键是否断裂的阈值；粘结半径为颗粒间产生粘结键所需要的最大间距。在离散元软件中，稻板田土壤颗粒由粘结状态到失效破坏的过程模型为：

粘结键受载迭代原理

(1)

式中Fn、Ft——粘结键法向、切向受力，N

Tn、Tt——粘结键法向、切向扭矩，N·m

vn、vt——法向、切向速度，m/s

ωn、ωt——法向、切向角速度，rad/s

Sn、St——法向、切向刚度，N/m3

A——接触面积，m2

J——惯性矩，m4

RB——粘结变径，m

δt——单位时间步长，s

粘结键断裂条件

(2)

式中σmax——法向临界应力，Pa

τmax——切向临界应力，Pa

1.2 旋耕模型参数类型及标定方案

离散元仿真参数由本征参数(土壤颗粒与旋埋刀辊材料的密度、泊松比、剪切模量)、材料接触参数(土壤颗粒间以及土壤颗粒与旋埋刀辊间的恢复系数、静摩擦因数、滚动摩擦因数)和接触模型参数(HertzMindlin with Bonding颗粒接触模型的5个参数)组成，通过借鉴文献成果、实际试验以及虚拟标定的方法获取。

本征参数仅与物料的材料属性相关，而其他仿真参数受物料尺寸、结构和接触关系等因素影响。对于土壤而言，尺寸小而尺度范围大，且外部轮廓多样，粒径配比[20]和刚性重叠球体簇[21-22]的方法虽可缩小土壤实物与模型的差距，但在离散元建模时仍不可避免忽略土壤大部分真实的微观结构，采用放大尺寸的圆球模拟土壤逐渐成为业界普遍共识，与接触相关的实测值对于简化后的圆球状土壤模型反而失去了适用性。参数虚拟标定是将仿真试验和真实试验相结合，通过数学方法得到仿真参数与试验指标之间的关系，最终以仿真值逼近试验值的形式获取与研究物料相匹配的参数。该方法完全适用于土壤这种复杂的研究对象，并已实现沙土[23]、沙壤土[24]、粘壤土[20,25]等多种土壤模型的构建。但一种土壤模型往往侧重于一种或一类土壤性质的表达，并不能包含该类土壤的所有特性，其模型参数应根据应用情况不同而有所改变，同时仅靠土壤模型无法描述土壤与应用设备间的接触情况，因此土壤模型区别于土壤应用模型。通过文献研究发现，现有土壤模型的构建均基于堆积角试验，堆积角往往是由松散颗粒物料在堆积过程中受重力影响形成。测量稻板田土壤堆积角的前提需对土壤进行破碎，且破碎程度影响测量结果，获取的接触参数仅能表征土壤在某一破碎程度下的堆积特征。稻板田土壤被农具扰动前应被视为土粒群相互粘结的紧实整体，耕后破碎情况复杂，显然堆积角试验不适用于稻板田旋耕研究。

选用何种方案标定接触参数，关系到模型的适用性。旋耕作业是由直线牵引运动与旋转运动复合而成，刀辊刀具由入土至出土过程土壤相互接触形式和作用形式十分复杂，大致分为入土、出土和回程3个过程，如图2所示，刀具在入土区间与实土接触，对土壤有剪切撕裂、挤压和滑移摩擦作用；出土区间与松土接触，对土壤提升抛撒并二次切削破碎土块；回程区间刀具与抛起的土壤发生冲击与碰撞。旋耕过程土壤力学行为的特殊性，也说明了接触情况的复杂性，这也是深松作业离散元模型无法直接应用于旋耕作业的原因，因此除旋耕试验本身，很难找出能直接表征旋耕过程中土壤破碎情况及土壤与刀辊接触情况的替代方案。

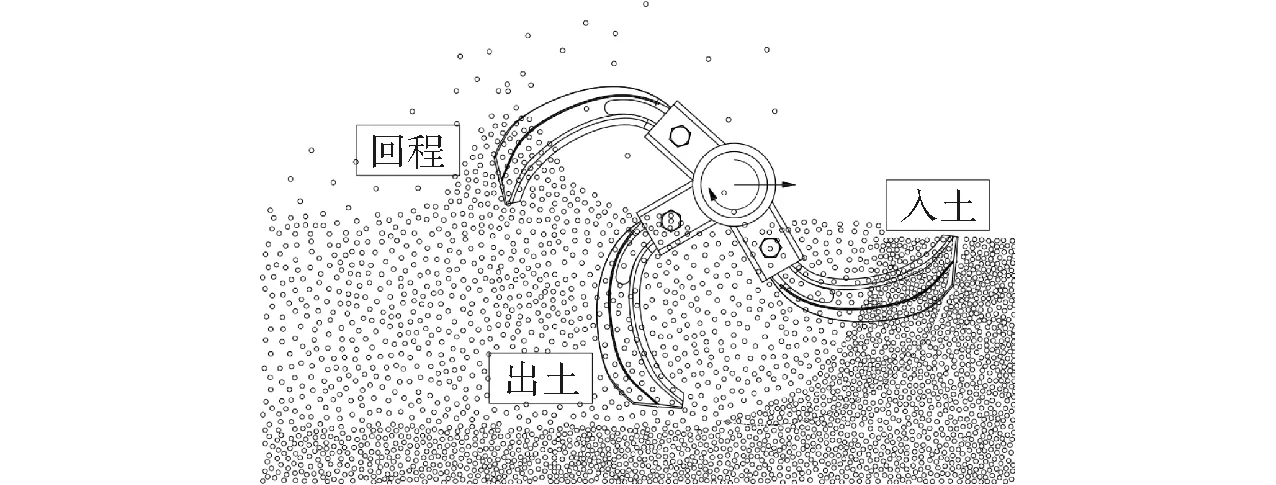
图2 旋耕作业过程示意图Fig.2 Schematic of rotary tillage process

根据图3可知，旋埋刀辊由6段组成，每段刀辊结构一致，沿幅宽方向缩小刀辊尺度，以1∶6缩比试制刀辊，并安装于旋耕测试平台内，将平台放置在稻板田土壤试验土槽上，其中土壤含水率23.37%，容重1 521 kg/m3。以前进速度0.6 m/s、刀辊转速280 r/min、耕深15 cm为工况，旋耕功耗为指标进行模型接触参数标定参照试验，试验过程如图4，每次试验后由测试平台的镇压装置将土面恢复至原有高度以确保土壤状态的一致性，试验共重复3次，结果见表1。

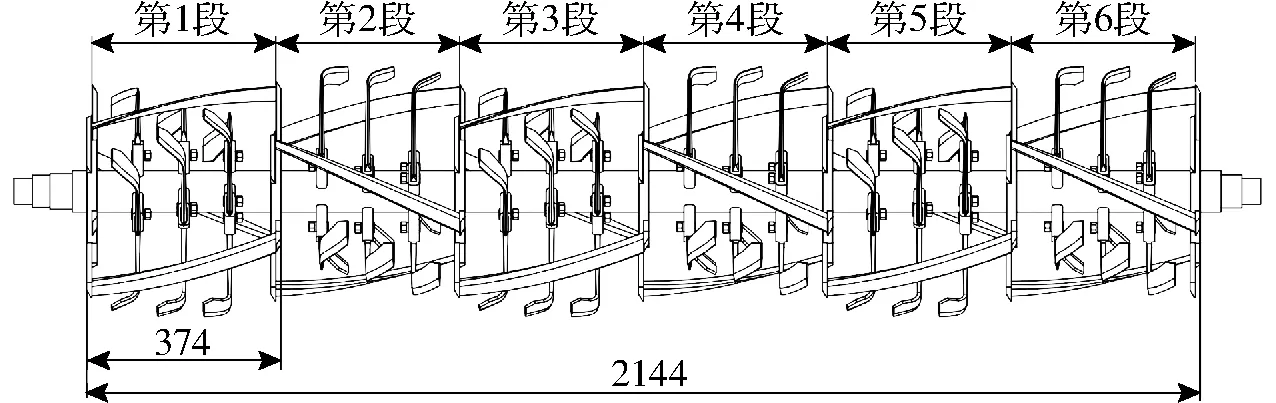
图3 旋埋刀辊结构图Fig.3 Structure drawing of rotary burying blade roller

图4 模型参数标定参照试验Fig.4 Model parameter calibration reference test

1.3 模型参数标定

1.3.1本征参数

本征参数为材料的固有特性，有相应参考资料和较为成熟的测量方法，其中刀辊材料参考了文献[26]；土壤泊松比和剪切模量由三轴压缩试验结果(弹性模量5×106Pa，内摩擦角23.8°)根据文献[23，25]的方法近似换算测得；颗粒密度通过颗粒填充试验由土壤容重校正获取，校正公式为

表1 旋耕功耗试验结果Tab.1 Test result of rotary tillage power consumption kW

(3)

式中ρ——颗粒密度，kg/m3

V——容器体积，m3

k——填充颗粒数量

r——颗粒半径，取4×10-3m

ρ1——土壤容重，kg/m3

最终确定的稻板田土壤与刀辊材料的本征参数如表2所示。

表2 模型本征参数Tab.2 Basic properties of models

1.3.2接触参数范围

接触参数中包含6个材料接触参数和5个模型接触参数。HertzMindlin with Bonding颗粒接触模型在应用时，常认为粘结行为源于土粒间的液桥，所以可用粘结半径衡量土壤含水率。所以假定土壤中的水分均匀分布，且包裹在土壤颗粒外围形成均匀水膜，水膜厚度与颗粒半径之和即为粘结半径，计算公式为

(4)

式中ω——土壤含水率，%

ρ2——水密度，kg/m3

根据HertzMindlin with Bonding颗粒接触模型应用于土壤耕作方面的研究成果[14,26-31]，综合分析后，确定其他接触参数的取值范围，如表3所示。

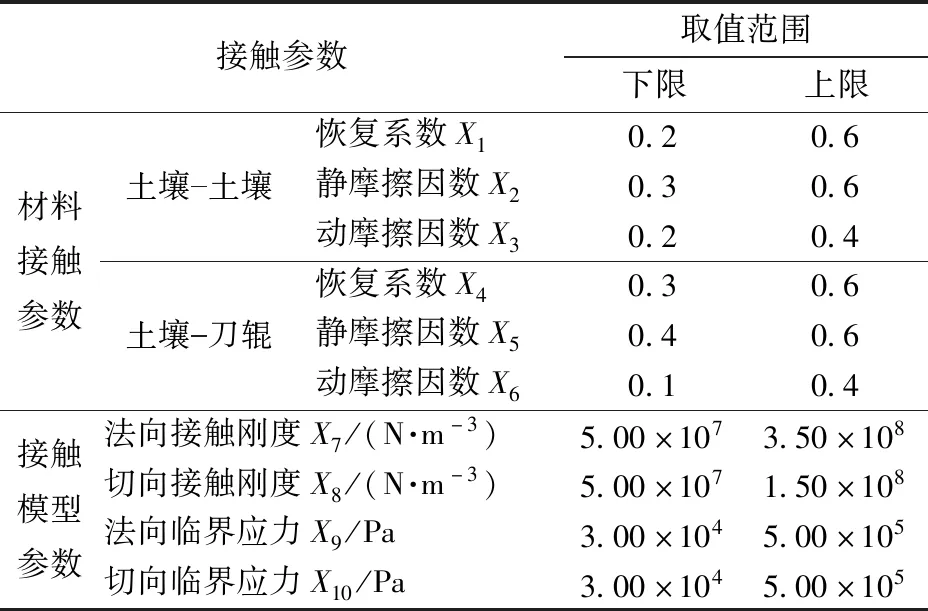
表3 待标定接触参数取值范围Tab.3 Range of contact parameters to be calibrated

1.3.3接触参数标定方法及结果

通过试验设计与数学方法令仿真值逼近测试值最终确定接触参数是离散元参数标定的主要途径。最陡爬坡标定方法[20,32]准确高效，在离散元参数标定的研究中得到广泛应用。该方法首先通过Plackett-Burman试验提取显著因素，然后以参照试验结果为目标值，将各显著因素以等步长增加的方式创建各步阶参数水平并开展仿真试验，通过相对误差变化趋势，进一步缩小参数范围，最后建立多因素回归模型并求解，完成参数标定。但最陡爬坡标定方法仍存在以下问题：Plackett-Burman试验对于因素显著性的判别存在争议[33]，现有文献也仅在定性的尺度上确定因素是否显著；当显著因素较多时，试验次数会成倍增加，导致回归模型的获取变得异常困难。

在对稻板田土壤与旋埋刀辊接触模型参数标定时，为避免上述问题，需对最陡爬坡试验方法进行优化。首先保留该方法中最核心的等步长爬坡思想，由于各因素以等步长增加方式进行仿真试验，步阶次序一旦确定，就间接确定该步阶次序下各因素取值，因此建立步阶次序与仿真指标间的函数关系，可达成指标值与各因素参数值的关联，起到类似回归模型的作用。

爬坡试验的起点参数组为A1(待标定接触参数的下限值)，终点参数组为Am(待标定接触参数的上限值)，则各步阶参数组可表示为

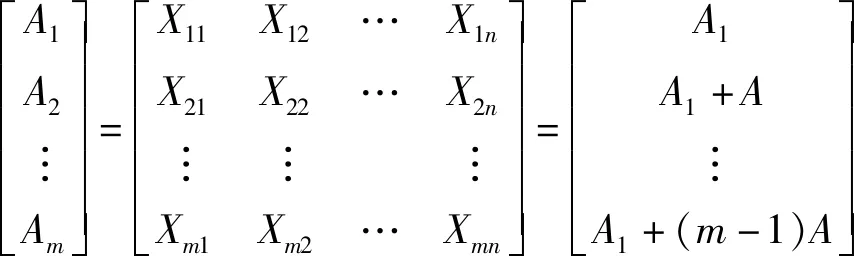
(5)

式(5)中m为爬坡的步阶总数(即标定试验总次数)，n为待标定参数总数量(n=10)，步长A为

(6)

步阶次序x的取值范围为1≤x≤m，对应各接触参数组的取值为

Ax=(x-1)A+A1

(7)

所以功耗P=f(X1，X2，X3，X4，X5，X6，X7，X8，X9，X10)可由式(7)转换为P=f(x)。

当m越大，各组标定试验的接触参数取值越接近，旋耕功耗随参数组的变化更加准确，但需要仿真的次数会增加，综合标定准确度与工作量，令m=9，建立旋埋刀辊与稻板田土壤颗粒在各步阶接触参数下的旋耕仿真模型，如图5所示，模型中土槽尺寸(长×宽×高)为1 200 mm×500 mm×300 mm，共计容纳441 185个土壤颗粒，刀辊工况与稻板田参照试验一致，刀辊转速280 r/min(0～1.1 s)，垂直入土速度1.50 m/s(0～0.1 s，耕深15 cm)，前进速度0.60 m/s(0.1～1.1 s)，数据以0.001 25 s为间隔保存，即刀辊旋转一周存储171个数据，刀辊平稳作业区间(0.1～1.1 s)旋转4.67圈，共计储存800个数据，从中选取刀辊运动的4个周期求功耗均值，功耗仿真结果如表4所示。

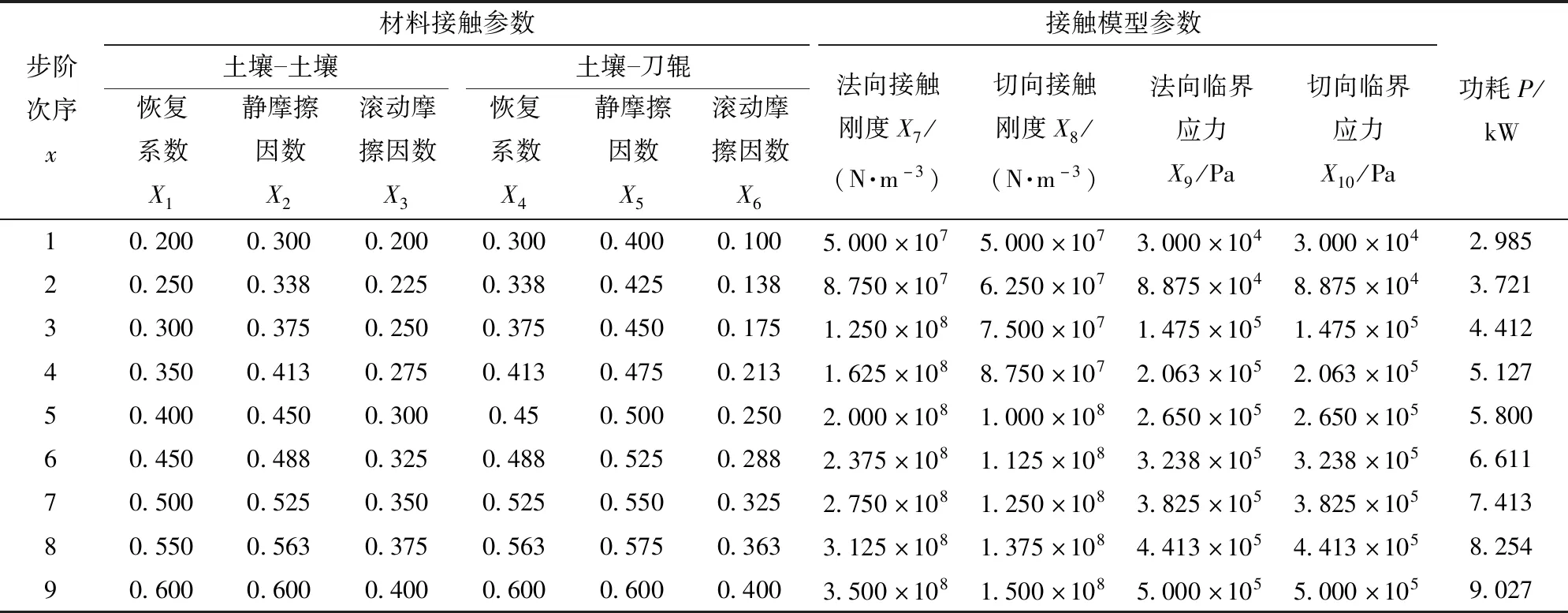
表4 仿真标定试验结果Tab.4 Result of simulation calibration test

图5 离散元标定试验仿真模型Fig.5 Discrete element calibration test simulation model

随着步阶次序增加，刀辊功耗单调递增，对仿真结果进行拟合，如图6所示。

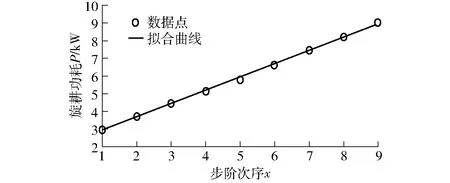
图6 仿真结果拟合曲线Fig.6 Fitting curve of simulation result

拟合方程为

P=0.754 2x+2.156 7

(8)

其中决定系数R2为0.998 7，说明拟合方程对仿真试验值的拟合程度较好。

将稻板田参照试验结果(表1)代入式(8)，求得步阶次序x=4.26，根据式(7)，最终获得稻板田土壤与旋埋刀辊相互作用对应的接触参数组A4.26，如表5所示。

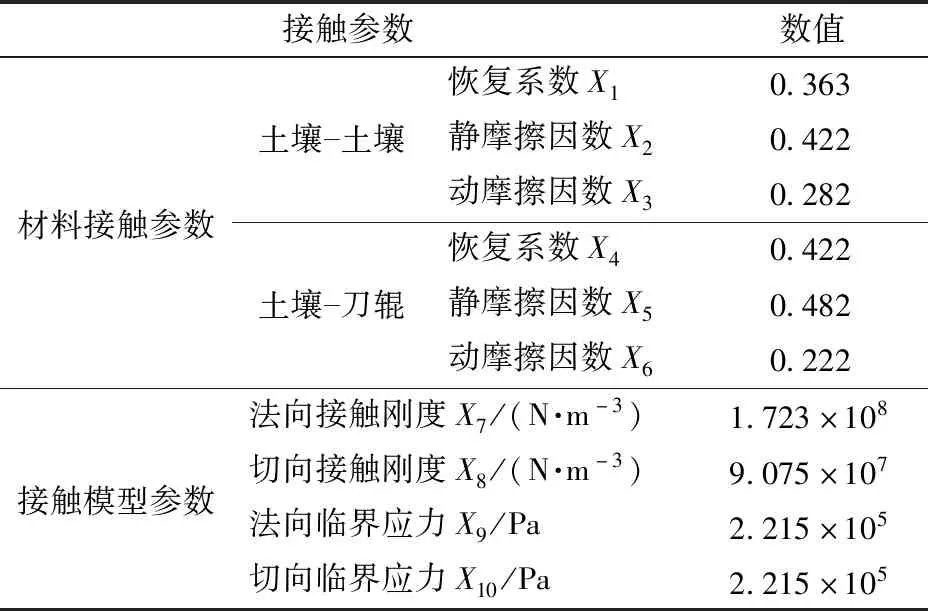
表5 接触参数标定结果Tab.5 Calibration results of contact parameters

将标定后的接触参数组A4.26输入EDEM软件中，进行仿真模型验证，得到旋耕功耗为5.269 kW，仿真预测值与实测值的相对误差为1.84%，差异较小，表明在等步长爬坡试验中利用步阶次序建立模型的方法可行，因此接触参数组A4.26能够反映旋埋刀辊与稻板田土壤在功耗指标下的离散元旋耕接触情况。

2 功耗预测模型验证

2.1 模型适用性分析

为检验该离散元模型的适用性，增加通用刀辊(图7)，利用旋耕平台分别以3种工况开展稻板田土槽试验和仿真试验，并计算仿真值相对于实测值的相对误差并取绝对值，结果如表6所示。

图7 刀辊实物图Fig.7 Physical map of blade roller

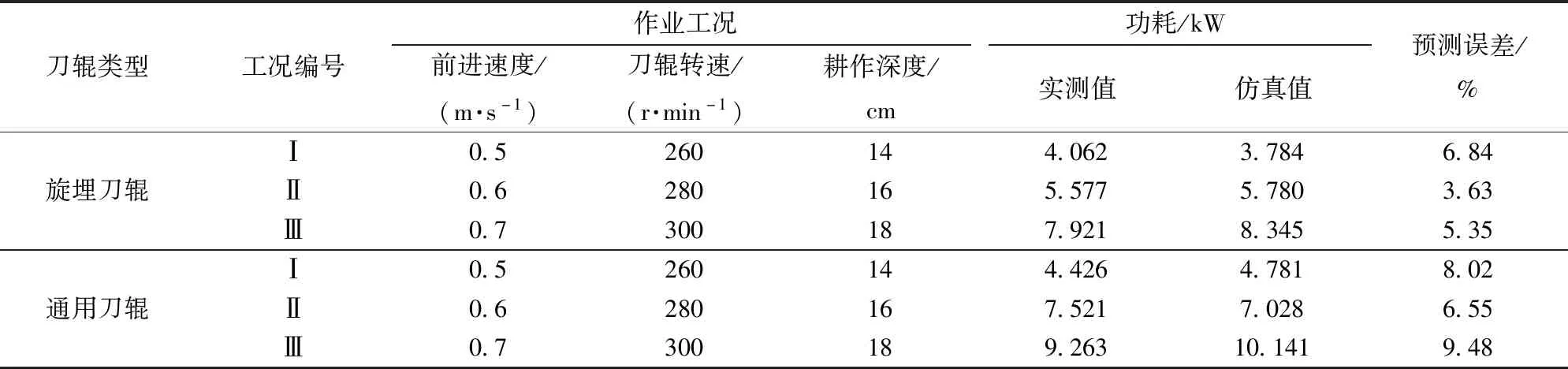
表6 误差对比试验设计与结果Tab.6 Error comparision test design and result

根据表6可知，预测误差均值为6.65%，范围在3.63%～9.48%之间；旋埋刀辊与通用刀辊的平均误差分别为5.28%和8.02%；工况Ⅰ、Ⅱ、Ⅲ的误差均值分别为7.43%、5.10%、7.42%。旋埋刀辊的功耗预测误差小于通用刀辊，说明用旋埋刀辊标定的离散元参数用于其他刀辊仿真研究时，可能会造成额外的误差，可能与模型中不同接触参数对刀辊结构变化引起功耗指标变化的敏感程度不同有关，原结构的标定结果可能忽略了对现结构较敏感的参数，造成了误差。以这种观点研究不同工况下的旋耕功耗时，发现工况Ⅱ的误差较小，相对于工况Ⅰ、Ⅲ，工况Ⅱ与标定工况差距较小，由此推断这种额外误差也有可能存在作业工况中。

对试验结果进行方差分析，如表7所示，在α=0.05水平下刀辊类型和作业工况对试验结果的影响不显著，说明从统计学观点可认为，该离散元模型在应用过程中误差并非来自刀辊类型和作业工况。

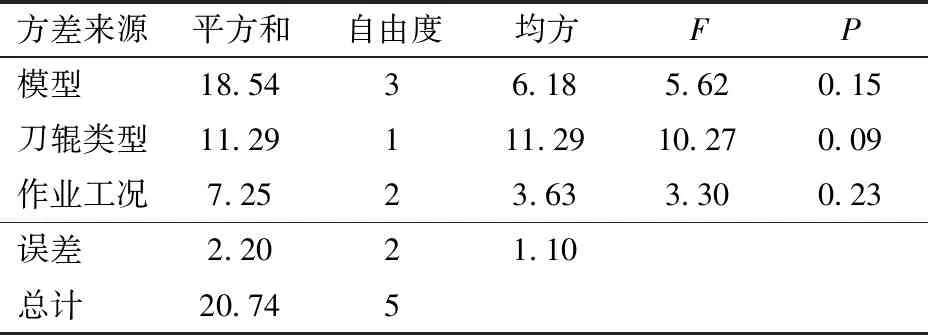
表7 方差分析Tab.7 Variance analysis

综上，功耗预测的相对误差均在合理范围，说明稻板田旋耕功耗预测模型基本满足应用需求，但对于一些结构或作业方式与旋耕作业差距较大的耕作部件(如犁、深松铲等)，该模型的适用性难以保证。

2.2 原尺度旋埋刀辊功耗预测

于2019年10月在华中农业大学现代农业科技试验基地开展试验。所选试验田内留有中稻秸秆，含水率为22.16%，容重为1.52×103kg/m3。刀辊安装在幅宽2.3 m的侧边传动旋耕机机架内，由东方红LX954型轮式拖拉机驱动，通过调节油门与挡位改变作业工况，功耗由动态转矩转速传感器(北京中航科仪测控技术有限公司，转速测量范围0～4 000 r/min，扭矩测量范围0～3 000 N·m) 测量，每种工况功耗重复3次，同时根据实测工况和表2、5的仿真参数建立稻板田旋耕功耗预测模型，进行仿真。田间试验与仿真试验过程如图8所示，功耗对比结果见表8。

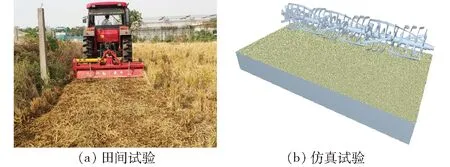
图8 旋埋刀辊功耗预测模型检验Fig.8 Power consumption prediction test of rotary buried blade roller

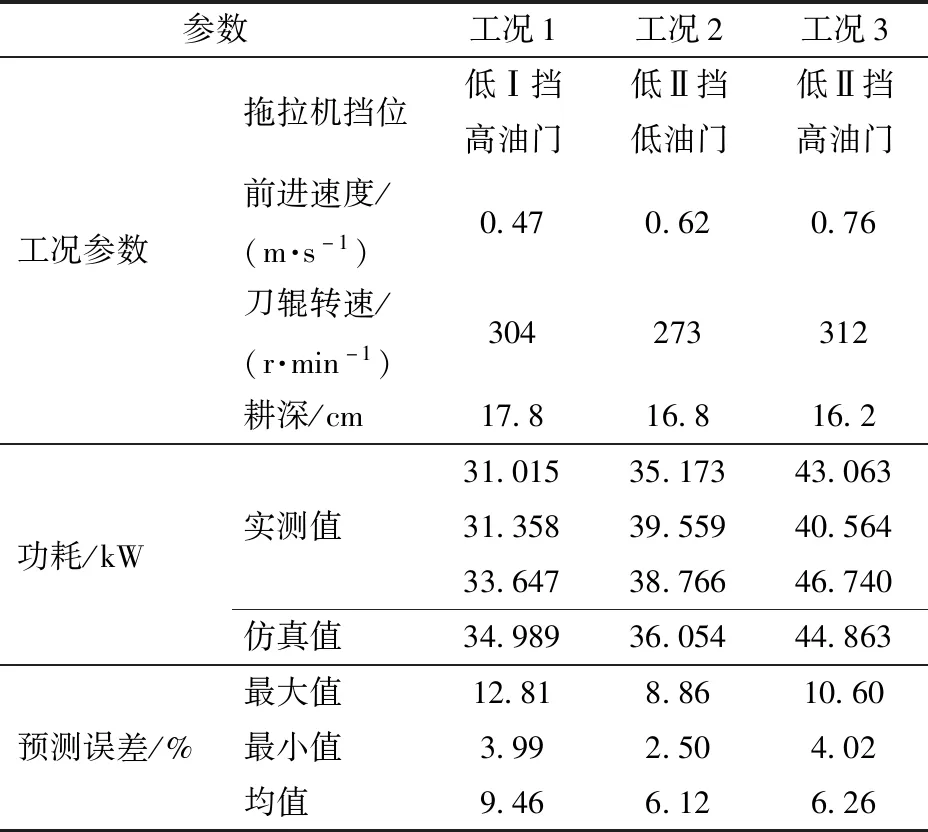
表8 功耗预测结果Tab.8 Power consumption prediction results

由表8可知，田间试验功耗预测误差范围在2.50%～12.81%之间，均值为7.28%，刀辊结构在缩放过程误差变化较小，说明离散元接触参数标定试验方案可行。根据每种工况的3次试验可知，极差分别为2.632、4.386、6.176 kW，与对应工况功耗均值的百分比依次为8.22%、11.59%、14.21%。田块区域土壤不均匀、机具操控不稳定等不可控因素的干扰使实测重复误差较大，当刀辊优化前后功耗变化小于重复误差时，单纯通过少量重复的田间试验很难验证优化结果，该稻板田旋耕功耗预测模型精度符合应用要求，能在一定误差范围内获取刀辊功耗，当模型输入参数变化，输出功耗随之响应，可为后续旋耕刀具减阻降耗的优化研究提供支持。

3 结论

(1)栽播冬油菜、冬小麦前稻板田土壤的含水率通常与其塑限接近，此时土壤不能承受较大的塑性形变，符合HertzMindlin with Bonding颗粒接触模型的模拟要求。

(2)土壤耕作由农具和土壤共同参与，参数标定时需同时考虑土壤与农具的接触特征。鉴于旋耕作业结构与运动的特殊性，结合旋埋刀辊的结构特点，沿幅宽方向以1∶6 缩比试制刀辊，进行标定参照试验；稻板田土壤与旋埋刀辊旋耕接触参数的虚拟标定采用等步长爬坡试验，通过步阶次序建立了接触参数与功耗指标之间的函数关系；结合标定参考试验功耗值，最终确定了稻板田旋耕功耗预测模型的接触参数取值，完成了模型的构建。

(3)为验证该模型的适用性，在不同工况下对通用刀辊和旋埋刀辊的旋耕功耗进行预测，预测误差范围为3.63%～9.48%，均值为6.65%，方差分析显示，稻板田旋耕功耗预测模型适用于不同旋耕刀辊及工况下的功耗预测。原尺度刀辊田间试验功耗预测误差范围为2.50%～12.81%，均值为7.28%，刀辊结构在缩放过程误差变化较小，说明模型能准确反映旋埋刀辊在稻板田作业的功耗情况。