波纹夹层板固有频率的一阶Zig-Zag 理论计算方法
王小明,魏 强
(1. 中国舰船研究设计中心,湖北 武汉 430064;2. 船舶振动噪声重点实验室,湖北 武汉 430064)
0 引 言
夹层板是由强度大的上下面板和密度较小的心层组成,通常上下面板可以是钢板,碳纤维或者玻璃钢等,心层可以是木材,铝蜂窝或者泡沫塑料。心层的设计还有一种思路来降低等效密度,可以把心层设计成空心的波纹状结构,通过粘结[1–2]或者激光焊接[3–4]与上下面板相连,这就是波纹夹层板(见图1)。这样组成的新结构具有比强度高、比刚度高的优点,经常被应用到航空航天工程,船舶海洋工程,建筑桥梁工程和车辆工程等。
对于夹层板固有频率的研究,最经典的著作是文献[5],其中以Hoff理论研究了夹层板的振动频率,分别研究了不同边界条件下,固有频率的计算方法。吴晖把夹层板看作正交异性体,借鉴文献[5]中的结论,认为垂直波纹方向的剪切刚度无限大,推导出固有频率的解析表达式[6];Hossein Zamanifar等运用精细切片法研究了夹层板的自由振动和强迫振动,通过等效参数,将三维的夹层板通过等效参数转化成二维正交异性板,求解了无量纲的自由振动频率,与前人的研究成果吻合一致[7]。Zig-Zag理论在复合材料或层合板领域应用很广泛[8–10]。白瑞祥等以3层均质复合材料(或等效成3层均质复合材料)夹层板为研究对象,引入一阶Zig-Zag理论,建立了夹层板自由振动的有限元模型,采用子空间迭代法求解自由振动固有频率[11]。对于上下面板之间是非连续介质的心层夹层板,目前采用一阶Zig-Zag理论来建立运动方程的文献很少。本文提出一种考虑波纹夹层板心层不连续形状的情况下,上下3层都应用一阶Zig-Zag理论建立夹层板的运动方程的方法。
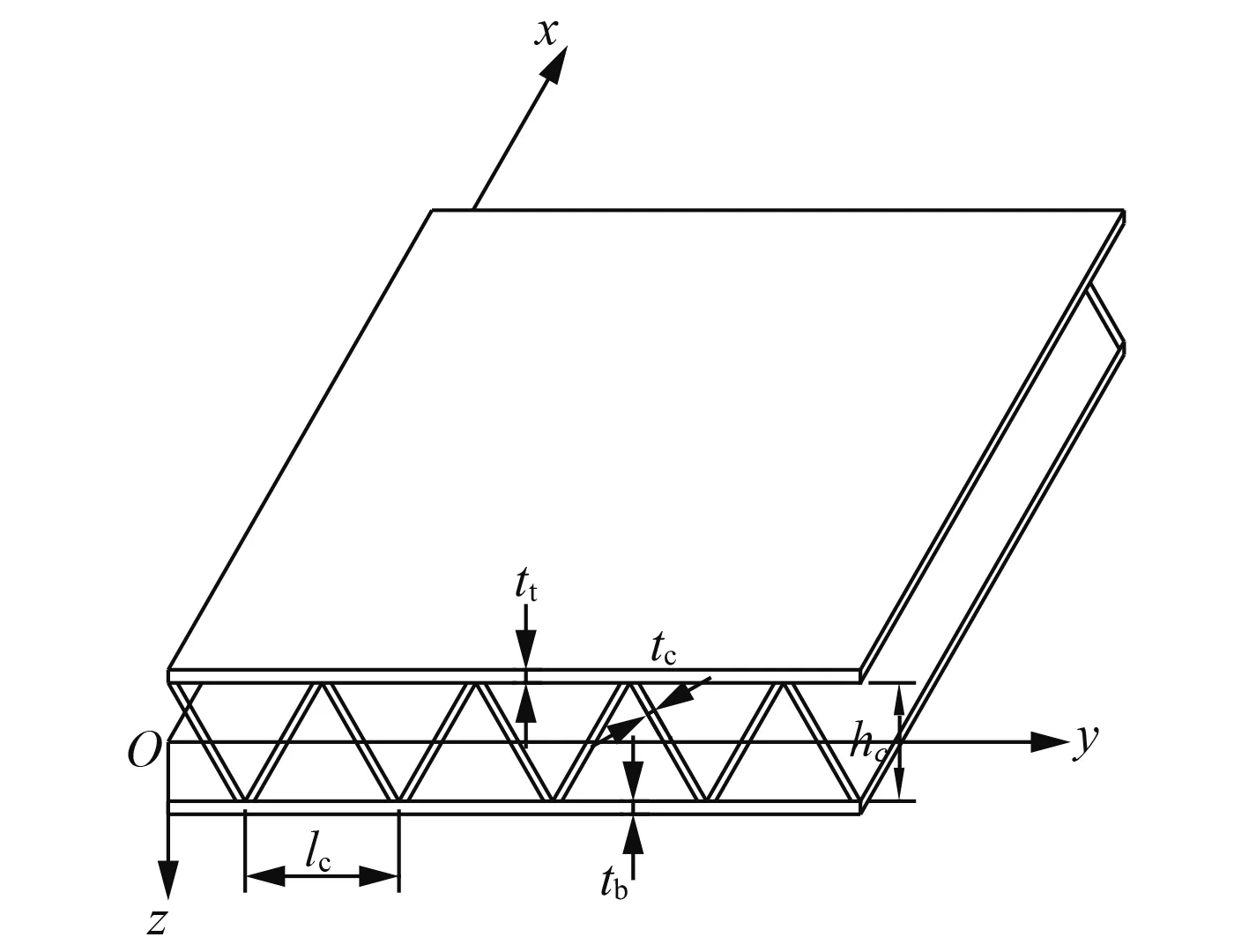
图1 波纹夹层板结构示意图Fig. 1 Corrugated sandwich structure
1 振动微分方程
如图2所示,波纹夹层板由上下面板和中间心层组成。在波纹夹层板中建立坐标系统。

图2 夹层板坐标系统Fig. 2 Coordinate system of corrugated sandwich
图中:tt为上面板厚度,tb为下面板厚度,tc为中间心层的厚度;心层的静高度为hc,心层的周期间距为lc。在线弹性理论分析,做以下基本假设:
1)夹层板的上下面板为普通薄板,考虑其抗剪作用,应用一阶剪切变形理论;
3)考虑心层的剪切作用,则心层中面法线在变形后保持为直线,但不再垂直于变形后的中面;
4)心层仅考虑其沿波纹方向的弯曲作用,忽略其垂直波纹方向的弯曲作用;
5)上下3层结构的面内位移沿板厚方向分段连续。
1.1 坐标系统与位移表达
根据假设1~假设4和图2中夹层板的坐标系统,上下面板的位移函数可以表示为:

式中:k取t,表示上面板;k取b,表示下面板。
心层的位移函数可以表示为:

根据假设5,可以列出位移连续条件如下:

将式(1)~式(5)代入式(7)~式(10),求出:

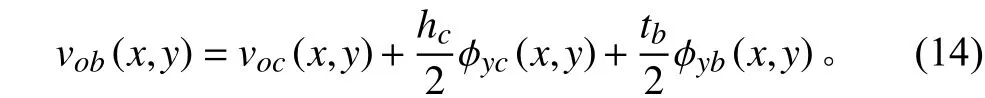
将式(11)~式(14)代入式(1)和式(2),联合式(3)~式(6),则所有的位移函数都用心层的中面位移函数表达。
应用弹性理论的应变位移关系,对于上面板:
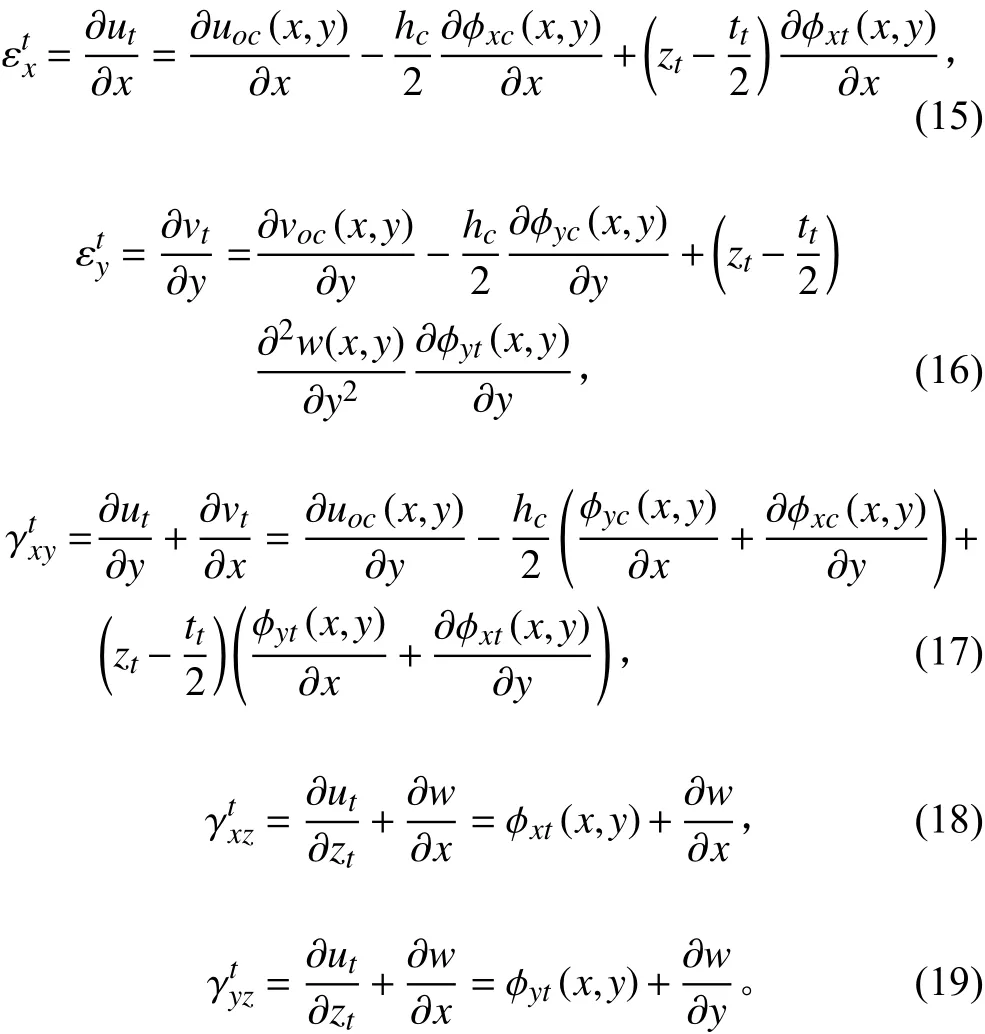
对于下面板也可以类似推导。
对于心层,正应变和剪应变分别为:

1.2 物理方程
上下面板和心层的每一个构件材料,认为它是各向同性的,则由弹性理论可以求出应力。
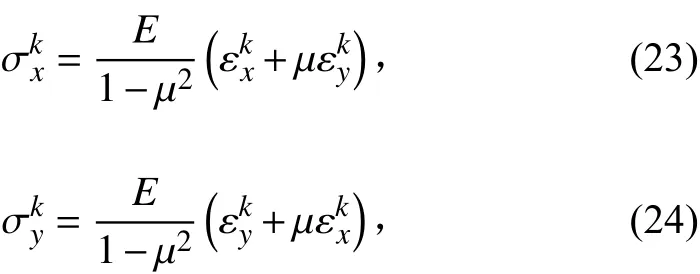
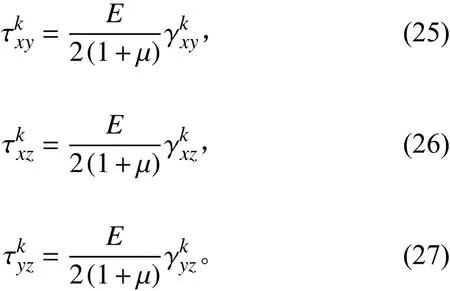

根据文献[12]和文献[13]的结论,心层yz平面的剪切弹性模量可表达为:

1.3 能量原理
哈密尔顿(Hamilton)原理提出稳定系统的动能和势能之差(动势)必然是最小值。对于振动分析的波纹夹层板而言,系统存在动能T和势能U,但是没有外力做功,势能仅包括系统的应变能。根据变分法,则应该使得

系统的动能包括3部分,分别是上下面板动能和心层动能。

系统的势能主要是指构件的应变能,应变能也包括3部分,分别是上下面板应变能和心层应变能。

其中:

将式(33)~(38)代入式(32),应用变分法中的拉格朗日–欧拉方程,经过复杂的推导、运算,得出以下振动微分方程:

2 边界条件与方程求解
对于简支的夹层板,其边界条件为:在x=0或a

在y=0或b
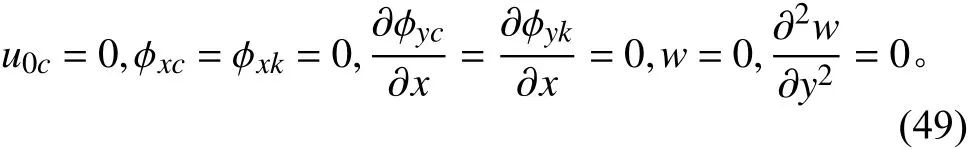
根据边界条件式(48)和式(49),可以取双傅里叶级数为式(39) ~ 式(47)的解,则
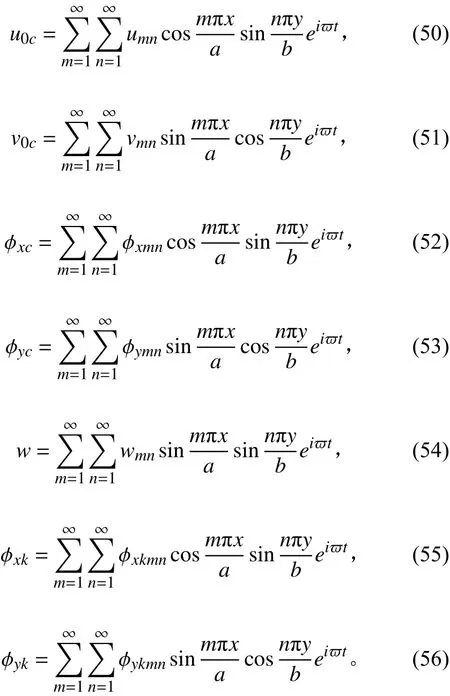
将式(50)~式(56)代入式(39)~式(47),然后比较两边的系数,则可以列出关于,,的方程组,要使得这些系数有非零解,必然使得系数行列式为零。这个系数行列式就是关于固有角频率的十八次多项式,解出这个十八次方程,取最小的正根就是所要求的固有角频率,则固有频率
3 方法验证
夹层板四边简支,长边a=2 000 mm,短边b=1 500 mm,上下面板厚度tt=tb=3 mm,心层厚度tc=2 mm,心层静高度hc=40 mm,心层周期间距lc=50 mm,上下面板和夹心都是同样材料,弹性模量E=Ec=2.1×105MPa,泊松比计算其横向微振动的固有频率。
为了形成对比,验证方法的准确性,分别用4种方法分别计算这个算例。
1)方法1
按照文献[5]所列公式计算固有频率(即Hoff理论),不过其中的剪切刚度不能采用连续介质心层的公式,而是采用等效剪切刚度,即采用式(56);
2)方法2
按照文献[6]中所列公式求解(即简化的Reisser理论),其中的剪切刚度也是采用方法1中的等效剪切刚度;
3)方法3
采用Ansys软件,用shell181单元模拟面板和心层,三维有限元计算固有频率;
4)方法4
本文方法。
表1列出了这4种方法计算的前9阶固有频率。从表1看出关于前8阶固有频率,上述4种方法的计算结果都非常接近,误差小于10%。因此本文的计算方法是有效可信的。

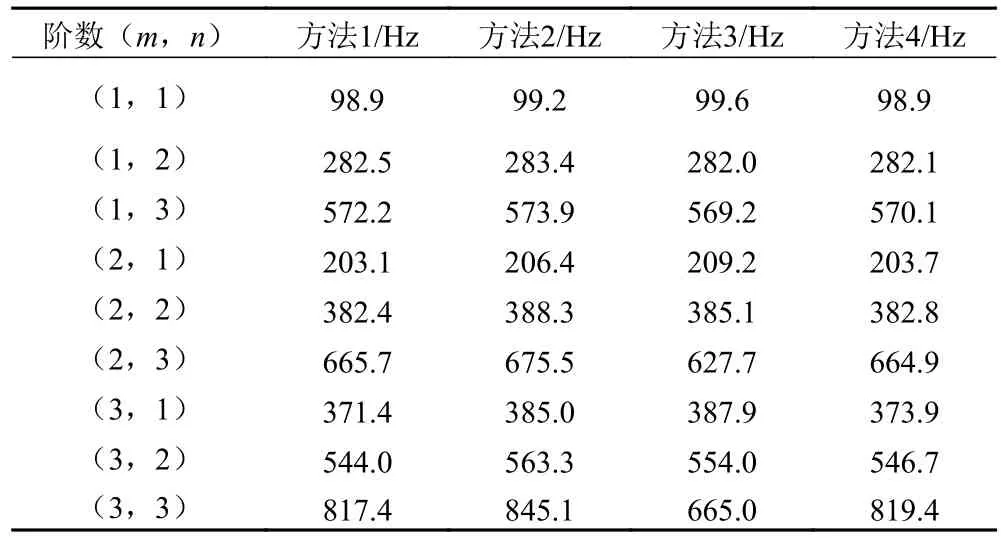
表1 各种方法关于前9阶频率的计算结果Tab. 1 Calculation results of freconcy from above methods
4 面板剪切作用的体现
当面板厚度较小的时候,忽略面板的剪切作用造成的误差是很小的。但是当面板厚度增加,剪切作用就表现比较明显。以第4节中算例的参数为基础,固定其他变量,分别以面板厚度和心层厚度为自变量,一阶频率为因变量,图3为不同方法计算的夹层板一阶频率随面板厚度变化曲线(上下面板相等,且同步变化),图4为不同方法计算的夹层板一阶频率随心层厚度变化曲线。
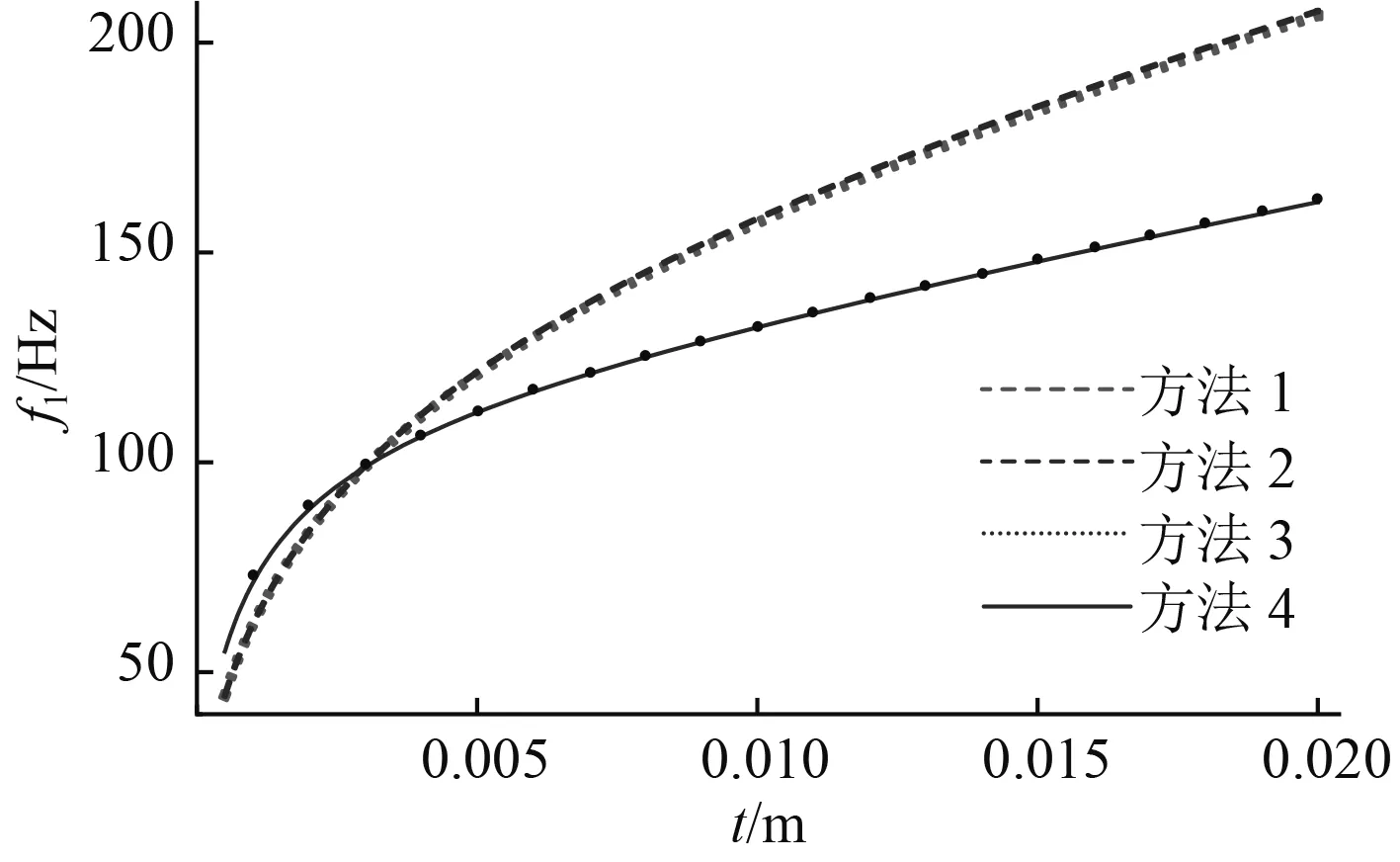
图3 面板厚度与一阶频率关系曲线Fig. 3 Face sheet thinkness and first order frequency relationship curves

图4 心层厚度与一阶频率关系曲线Fig. 4 Core sheet thinkness and first order frequency relationship curves
从图3和图4看出,面板厚度较小,不同方法计算的结果差别很小,面板厚度大于5 mm后,差别则很明显。同时,因为各类方法都考虑了心层的剪切作用,不管心层厚度如何变化,不同计算方法计算的固有频率都很接近。
5 结 语
通过应用一阶Zig-zag理论,同时考虑心层的实际形状,建立波纹夹层板的振动微分方程。用算例验证了本方法计算的前8阶固有频率的计算误差都在10%以内。
波纹夹层板面板板厚较小,忽略面板剪切作用的影响,导致的计算误差可以忽略;当面板厚度大于心层厚度1/8时,则误差是明显的,并且厚度越大,误差也越大。
因为Hoff理论中考虑了心层的剪切作用,因此波纹心层厚度的增加,不管是用Hoff理论计算还是简化的Hoff理论计算,都与本文方法计算结果极为接近。

